Макс Невелов Фактчек
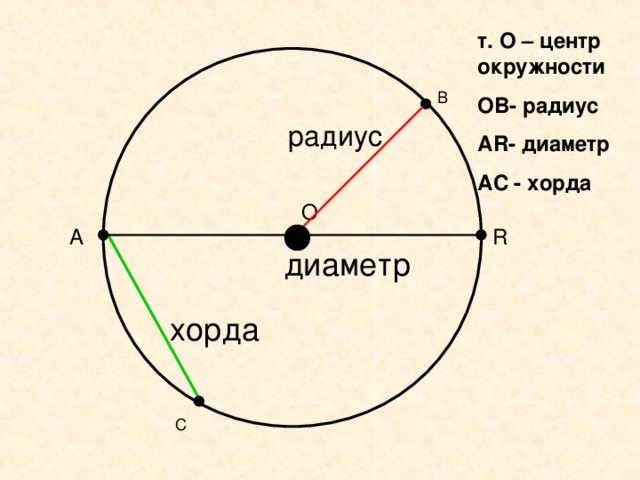
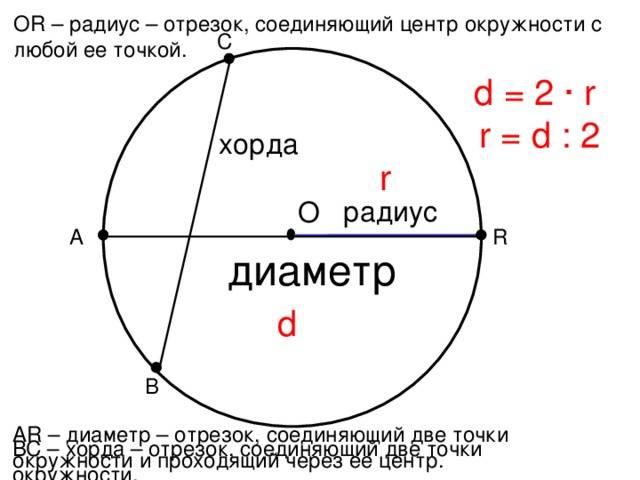
- Окружность – это замкнутая кривая, все точки которой равноудалены от центра. Элементами окружности являются радиус, диаметр, хорда, дуга.
- Круг – это геометрическая фигура, которая ограничена окружностью. Помимо радиуса, диаметра и хорды, в круге может встретиться сегмент и сектор.
- Вся дуга окружности имеет величину 360 градусов. Тогда половина дуги будет равняться 180 градусам.
- В окружности встречаются центральные и вписанные углы. При этом вписанный угол равен половине дуги, на которую он опирается, а центральный угол равен градусной мере дуги, на которую он опирается. Как следствие, если центральный и вписанный углы опираются на одну дугу, то центральный угол равен двум вписанным углам.
Работа 1. что такое цикл?
- Замкнутая кривая, все точки которой равноудалены от центра;
- Геометрическая фигура, которая ограничена замкнутой кривой, все точки которой равноудалены от центра;
- Геометрическая фигура, которая имеет круглую форму;
- Часть плоскости, ограниченная замкнутой кривой, все точки которой равноудалены от центра.
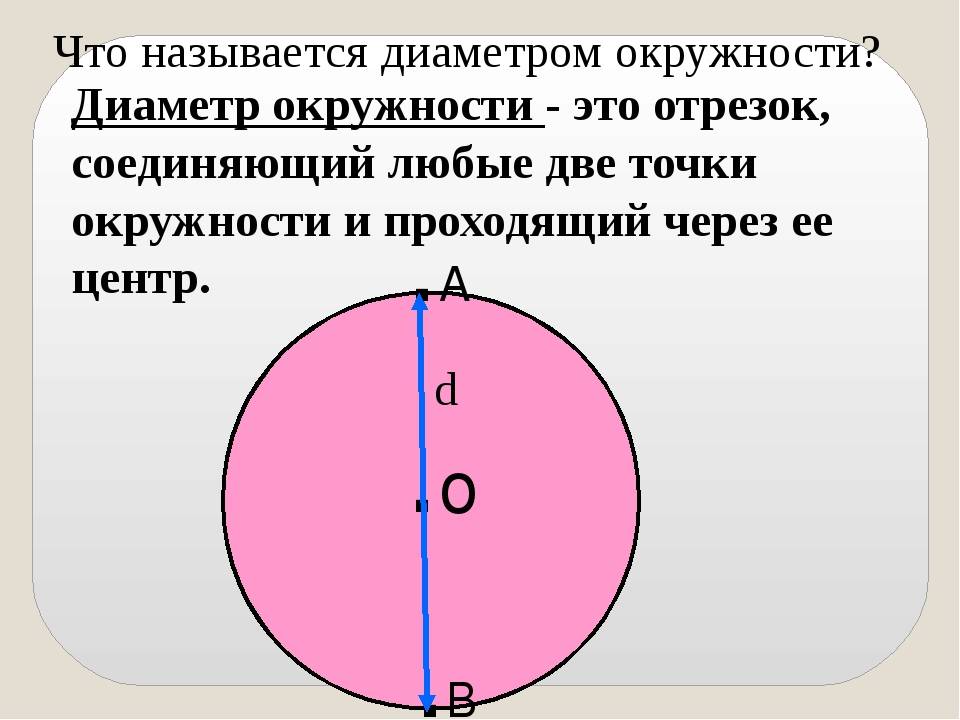
Работа 2. Каков диаметр круга?
- Это отрезок, соединяющий центр окружности и любую точку на окружности;
- Это отрезок, соединяющий две произвольные точки на окружности;
- Это отрезок, соединяющий две точки на окружности и проведенный через центр окружности;
- Это половина дуги окружности.
Работа 3. Какой тип можно использовать для нахождения длины окружности?
Работа 4: В круге выгравирован лук 60 градусов. Какая пропорция периметра у этого лука?
Вопрос 5: Угол регистрации составляет 50 градусов. Каков центральный угол на той же дуге?
Ответы: 1. -1 2. -3 3. -2 4. -3 5.
Как же определить длину этого особого отрезка?
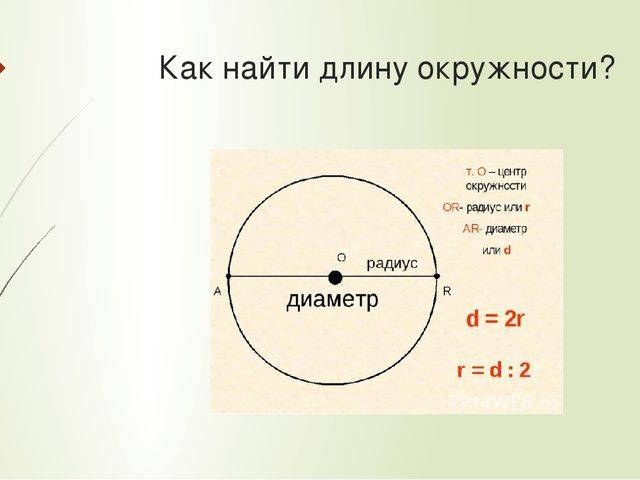
Как мы будем вычислять, зависит от того, что мы об этой самой окружности знаем. Предположим, нам известен её радиус… напомним: радиусом мы именуем отрезок, который соединяет точку в центре окружности с любой точкой, лежащей на её поверхности. Если мы проведём два таких радиуса, то часть окружности, которую мы таким образом «отсекли», будет называться сектором.
Так вот, нетрудно заметить, что располагающаяся в центре точка рассекает диаметр на два радиуса. Окружность же представляет собой совокупность точек, равно удалённых от заданной точки (центра), следовательно, радиусы – где бы мы их ни проводили, с какой бы из тачек окружности ни соединяли её центр – будут иметь одинаковую длину, и к двум радиусам, составляющим диаметр, это тоже относится. Таким образом, если нам известен радиус, остаётся только умножить его величину на два – вот вам и величина диаметра!
Несколько сложнее обстоит дело, если радиуса мы не знаем, но известен нам периметр окружности (проще говоря, её длина – то, что получится, если окружность «развернуть» и измерить. Тут в дело вступает величина совершенно особая – число пи. Число это иррациональное – т.е. представляет собой десятичную дробь, которая никогда не заканчивается, но при этом периодической она тоже не является. Но для удобства используют округлённое значение 3,14. Упоминания о некой константе, выражающей соотношение между длиной окружности и диаметром, мы находим уже у мудрецов Древнего Египта и Вавилона, внесли свой вклад в его вычисление и Архимед, и древнекитайские математики Чжан Хэн, Лю Хуэй и Цзу Чунжи, а греческой буквой пи его впервые обозначил английский математик Джонс в XVIII в. – той самой буквой, с которой начинается слово «периметр» и греческое слово, обозначающее окружность.
Соотношение выражается формулой P=2πR, т. е 2 умножить на число пи и на радиус. Но, поскольку мы знаем, что диаметр равен двум радиусам, можно сказать, что периметр равен произведению числа пи и диаметра. Следовательно, разделив периметр на число пи, получим диаметр.
Если же нам известна площадь круга, то удобнее всего сначала найти радиус. Напомним, площадь круга мы находим, умножая число пи на квадрат радиуса. Если мы площадь разделим на число пи, а потом извлечём корень квадратный из результата, это и будет радиус. Остаётся только умножить его на два – и мы получим диаметр.
Дюймы против мм. Откуда путаница и когда необходима таблица соответствия
Трубы, диаметр которых обозначается дюймами (1″, 2″
) и/или долями дюймов (1/2″, 3/4″
), являются общепринятым стандартом в водо – и водогазоснабжении.
Как правило монтаж дюймовых труб проходит без затруднений, но при их замене на трубы из пластика, меди и нержавеющей стали возникает проблема – несоответствие размера обозначенного дюйма (33,5 мм
) к его реальному размеру (25,4 мм
).
Обычно этот факт вызывает недоумение, но если глубже заглянуть в процессы происходящие в трубе, то логика несоответствия размеров становится очевидна и непрофессионалу. Все довольно просто – читайте дальше.
Дело в том, что при создании водного потока ключевую роль играет не внешний, а внутренний диаметр и по этой причине для обозначения используется именно он.
Однако несоответствие обозначаемых и метрических дюймов все равно остается, т. к. внутренний диаметр стандартной трубы составляет 27,1 мм
, а усиленной – 25,5 мм
. Последнее значение стоит довольно близко к равенству 1″”=25,4
но все же им не является.
Разгадка состоит в том, что для обозначения размера труб применяется номинальный, округленный до стандартного значения диаметр (условный проход Dy
). Величина условного прохода подбирается так, чтобы пропускная способность трубопровода увеличивалась от 40 до 60%
в зависимости от роста величины индекса.
В ситуациях с пластиковыми трубами для решения проблемы несоответствующих размеров используются переходные элементы. При необходимости заменить или состыковать дюймовые трубы с трубами, выполненными по реальным метрическим размерам – из меди, нержавейки, алюминия, следует брать во внимания и наружный, и внутренний диаметры.
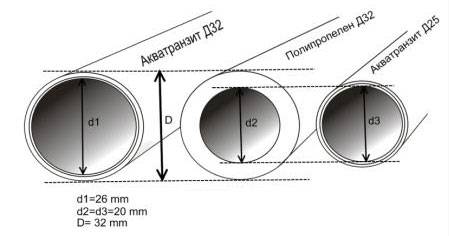
Таблица соответствия условного прохода дюймам
| Ду | Дюймы | Ду | Дюймы | Ду | Дюймы |
| 6 | 1/8″ | 150 | 6″ | 900 | 36″ |
| 8 | 1/4″ | 175 | 7″ | 1000 | 40″ |
| 10 | 3/8″ | 200 | 8″ | 1050 | 42″ |
| 15 | 1/2″ | 225 | 9″ | 1100 | 44″ |
| 20 | 3/4″ | 250 | 10″ | 1200 | 48″ |
| 25 | 1″ | 275 | 11″ | 1300 | 52″ |
| 32 | 1(1/4)” | 300 | 12″ | 1400 | 56″ |
| 40 | 1(1/2)” | 350 | 14″ | 1500 | 60″ |
| 50 | 2″ | 400 | 16″ | 1600 | 64″ |
| 65 | 2(1/2)” | 450 | 18″ | 1700 | 68″ |
| 80 | 3″ | 500 | 20″ | 1800 | 72″ |
| 90 | 3(1/2)” | 600 | 24″ | 1900 | 76″ |
| 100 | 4″ | 700 | 28″ | 2000 | 80″ |
| 125 | 5″ | 800 | 32″ | 2200 | 88″ |
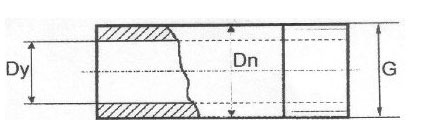
Таблица соответствия диаметра условного прохода, резьбы и наружных диаметров трубопровода в дюймах и мм.
Условный проход трубы Dy. мм | Диаметр резьбы G”. дюйм | Наружный диаметр трубы Dn. мм | ||
Трубы стапьные водо/водогазoпроводные ГОСТ 3263-75 | Трубы стальные эпектросварные прямошовные ГОСТ 10704-91. Трубы стальные бесшовные горячедеформированные ГОСТ 8732-78. ГОСТ 8731-74 (ОТ 20 ДО 530 мл) | Полимерная труба. ПЭ, ПП, ПВХ | ||
ГОСТ
– государственый стандарт, используемый в тепло – газо – нефте – трубопроводах
ISO
– стандарт обозанчения диаметров, используется в сантехнических инженерных системах
SMS
– шведский стандарт диаметров труб и запорной арматуры
DIN / EN
– основной евросортамент для стальных труб по DIN2448 / DIN2458
ДУ (Dy)
– условный проход
Таблицы с размерами полипропиленовых труб представлены в следующей статье >>>
Таблица соответствия условного диаметра труб с международной маркировкой
| ГОСТ | ISO дюйм | ISO мм | SMS мм | DIN мм | ДУ |
| 8 | 1/8 | 10,30 | 5 | ||
| 10 | 1/4 | 13,70 | 6,35 | 8 | |
| 12 | 3/8 | 17,20 | 9,54 | 12,00 | 10 |
| 18 | 1/2 | 21,30 | 12,70 | 18,00 | 15 |
| 25 | 3/4 | 26,90 | 19,05 | 23(23) | 20 |
| 32 | 1 | 33,70 | 25,00 | 28,00 | 25 |
| 38 | 1 ¼ | 42,40 | 31,75 | 34(35) | 32 |
| 45 | 1 ½ | 48,30 | 38,00 | 40,43 | 40 |
| 57 | 2 | 60,30 | 50,80 | 52,53 | 50 |
| 76 | 2 ½ | 76,10 | 63,50 | 70,00 | 65 |
| 89 | 3 | 88,90 | 76,10 | 84,85 | 80 |
| 108 | 4 | 114,30 | 101,60 | 104,00 | 100 |
| 133 | 5 | 139,70 | 129,00 | 129,00 | 125 |
| 159 | 6 | 168,30 | 154,00 | 154,00 | 150 |
| 219 | 8 | 219,00 | 204,00 | 204,00 | 200 |
| 273 | 10 | 273,00 | 254,00 | 254,00 | 250 |
Диаметры и другие характеристики трубы из нержавеющей стали
| Проход, мм | Диаметр наружн., мм | Толщина стенок, мм | Масса 1 м трубы (кг) | ||
| стандартных | усиленных | стандартных | усиленных | ||
| 10 | 17 | 2.2 | 2.8 | 0.61 | 0.74 |
| 15 | 21.3 | 2.8 | 3.2 | 1.28 | 1.43 |
| 20 | 26.8 | 2.8 | 3.2 | 1.66 | 1.86 |
| 25 | 33.5 | 3.2 | 4 | 2.39 | 2.91 |
| 32 | 42.3 | 3.2 | 4 | 3.09 | 3.78 |
| 40 | 48 | 3.5 | 4 | 3.84 | 4.34 |
| 50 | 60 | 3.5 | 4.5 | 4.88 | 6.16 |
| 65 | 75.5 | 4 | 4.5 | 7.05 | 7.88 |
| 80 | 88.5 | 4 | 4.5 | 8.34 | 9.32 |
| 100 | 114 | 4.5 | 5 | 12.15 | 13.44 |
| 125 | 140 | 4.5 | 5.5 | 15.04 | 18.24 |
| 150 | 165 | 4.5 | 5.5 | 17.81 | 21.63 |
Какую трубу считать малой – средней -большой?
Даже в серьезных источниках мне приходилось наблюдать фразы типа: «Берем любую трубу среднего диаметра и…», но какой этот средний диаметр никто не указывает.
Чтобы разобраться, стоит сначала понять на какой диаметр нужно ориентироваться: он может быть внутренним и внешним. Первый важен при расчете транспортировочной способности воды или газа, а второй для определения возможности выдерживать механические нагрузки.
Внешние диаметры:
От 426 мм считается большим;
102-246 называют средним;
5-102 классифицируется, как маленький.
Что касается внутреннего диаметра, то лучше заглянуть в специальную таблицу(см. выше).
Формулы для окружности и круга
Мы рассмотрели окружности и круг, а также их элементы, однако ни одну задачу не получится решить без формул. Давайте рассмотрим их.
Однако перед этим необходимо ввести еще несколько терминов.
Длина окружности – это длина кривой, которая образует окружности.
Если мы с помощью сантиметровой ленты измерим длину нашего обруча, то как раз получим длину окружности.
Длина дуги – это длина части кривой, которая образует окружность.
Отличие от длины окружности только в том, что тут измеряется не вся кривая, а только ее часть.
В таблице ниже приведены основные формулы, которые могут встретиться при решении задач.
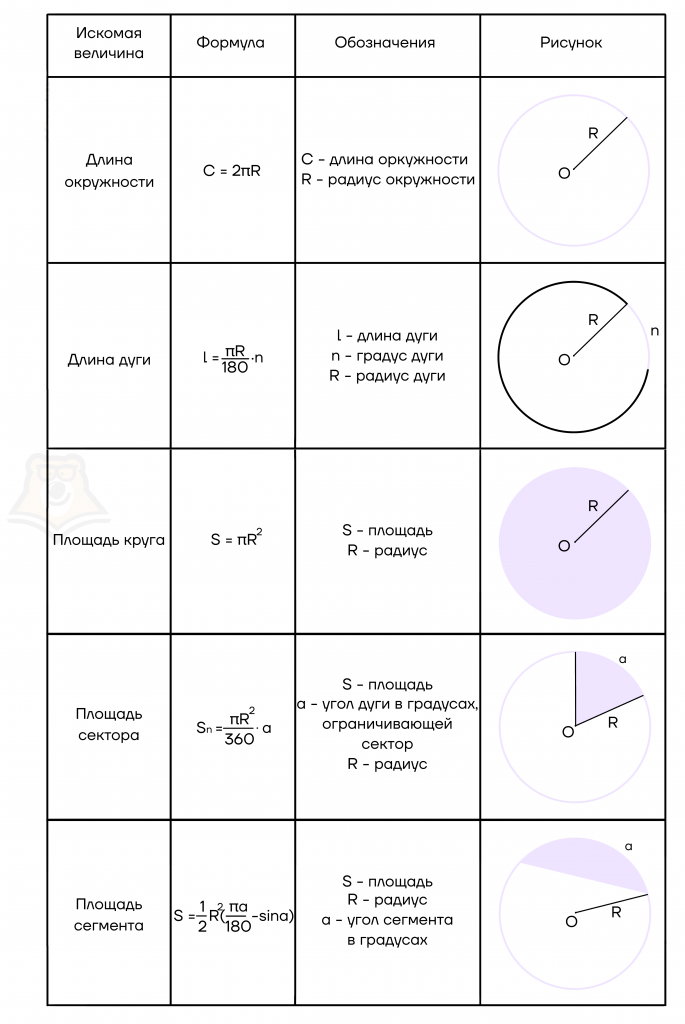
Применение и формула
Зная диаметр окружности, можно осуществлять строительство жилых домов, развлекательных центров, супермаркетов. Инженеры-конструкторы, занимающиеся разработкой разнообразных машин, агрегатов, механизмов, постоянно сталкиваются с подобными вычислениями. Какова формула диаметра данной кривой? Вычерчивают ее с помощью циркуля. В математике применяется прием косвенного вычисления длины окружности.
Самым простым способом является использование радиуса. Диаметр вычисляется как два радиуса. При заданной длине окружности можно определить ее диаметр путем деления длины на число «пи». К примеру, при длине 10 сантиметров диаметр будет составлять 10: 3,14 = 3,18 сантиметра.
При заданной площади круга, вычисление диаметра проводят путем извлечения квадратного корня из данного числа, затем деления полученного ответа на число «пи». К примеру, при площади круга 25 квадратных сантиметров, квадратный корень составит 5 сантиметров, а после деления этого числа на 3,14, получим 1,59 см. Это и есть диаметр данной в задаче окружности.
Справиться с такими несложными вычислениями может и рядовой ученик школы, и инженер конструкторского бюро.
Данный урок посвящён изучению окружности и круга. Также учитель научит отличать замкнутые и незамкнутые линии. Вы познакомитесь с основными свойствами окружности: центром, радиусом и диаметром. Выучите их определения. Научитесь определять радиус, если известен диаметр, и наоборот.
Касательная к окружности
Касательной к окружности
принято называть прямую, у которой имеется одна общая точка с окружностью.
Если же у прямой есть две общие точки, ее называют секущей
.
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
AC = CB
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть.
AC^{2} = CD \cdot BC
Можно сделать вывод: произведение целого отрезка первой секущей на его внешнюю часть равняется произведению целого отрезка второй секущей на его внешнюю часть.
AC \cdot BC = EC \cdot DC
Виды стальных труб по способу их производства
Электросварные (прямошовные)
Для их изготовления применяют штрипс или листовую сталь, которые на специальном оборудовании изгибаются в нужном диаметре, а затем концы соединяются с помощью сварки.
Воздействие электросварки гарантирует минимальную ширину шва, что делает возможным их применение для сооружения газопроводов или водопроводов. Металл в большинстве случаев углеродистый или низколегированный.
Показатели готовых изделий регламентируются следующими документами: ГОСТ 10704-91, ГОСТ 10705-80 ГОСТ 10706-76
.
При этом обратите внимание, что труба, изготовленная согласно стандарту 10706-26 отличается максимальной прочностью среди себе подобных – после создания первого соединительного шва он укрепляется еще четырьмя дополнительными (2 внутри и 2 снаружи). В нормативной документации указываются диаметры изделий, произведенных путем электросварки
Их величина от 10 до 1420 мм
В нормативной документации указываются диаметры изделий, произведенных путем электросварки. Их величина от 10 до 1420 мм.
Спиральношовные
Материалом для производства служит сталь в рулонах. Продукция также характеризуется наличием шва, но в отличие от предыдущего способа производства он шире, а значит, способность выдерживать высокое внутреннее давление ниже. Поэтому их не применяют для сооружения газопроводных систем.
Регламентируется конкретный вид труб ГОСТом под номером 8696-74
.
Бесшовные
Производство конкретного вида подразумевает деформацию специально подготовленных заготовок из стали. Процесс деформации может выполняться как под воздействием высоких температур, так и холодным способом (ГОСТ 8732-78, 8731-74 и ГОСТ 8734-75 соответственно).
Отсутствие шва положительно сказывается на прочностных характеристиках – внутреннее давление равномерно распределяется по стенкам (нет «ослабленных» мест).
Что касается диаметров, то нормативы контролируют их изготовление со значением до 250 мм. Покупая продукцию с размерами, превышающими указанные, приходится рассчитывать только на добросовестность производителя.
Вашему вниманию ещё пара отличных слайдов креативной рекламы производителя труб:
Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты
, устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
Как же определить длину этого особого отрезка?
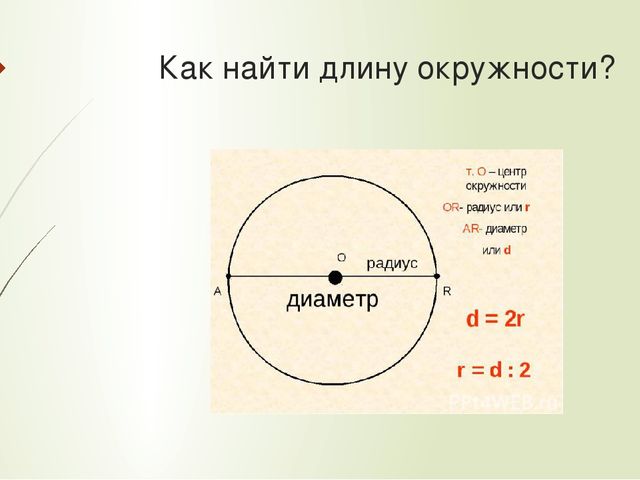
Как мы будем вычислять, зависит от того, что мы об этой самой окружности знаем. Предположим, нам известен её радиус… напомним: радиусом мы именуем отрезок, который соединяет точку в центре окружности с любой точкой, лежащей на её поверхности. Если мы проведём два таких радиуса, то часть окружности, которую мы таким образом «отсекли», будет называться сектором.
Так вот, нетрудно заметить, что располагающаяся в центре точка рассекает диаметр на два радиуса. Окружность же представляет собой совокупность точек, равно удалённых от заданной точки (центра), следовательно, радиусы – где бы мы их ни проводили, с какой бы из тачек окружности ни соединяли её центр – будут иметь одинаковую длину, и к двум радиусам, составляющим диаметр, это тоже относится. Таким образом, если нам известен радиус, остаётся только умножить его величину на два – вот вам и величина диаметра!
Несколько сложнее обстоит дело, если радиуса мы не знаем, но известен нам периметр окружности (проще говоря, её длина – то, что получится, если окружность «развернуть» и измерить. Тут в дело вступает величина совершенно особая – число пи. Число это иррациональное – т.е. представляет собой десятичную дробь, которая никогда не заканчивается, но при этом периодической она тоже не является. Но для удобства используют округлённое значение 3,14. Упоминания о некой константе, выражающей соотношение между длиной окружности и диаметром, мы находим уже у мудрецов Древнего Египта и Вавилона, внесли свой вклад в его вычисление и Архимед, и древнекитайские математики Чжан Хэн, Лю Хуэй и Цзу Чунжи, а греческой буквой пи его впервые обозначил английский математик Джонс в XVIII в. – той самой буквой, с которой начинается слово «периметр» и греческое слово, обозначающее окружность.
Соотношение выражается формулой P=2πR, т. е 2 умножить на число пи и на радиус. Но, поскольку мы знаем, что диаметр равен двум радиусам, можно сказать, что периметр равен произведению числа пи и диаметра. Следовательно, разделив периметр на число пи, получим диаметр.
Если же нам известна площадь круга, то удобнее всего сначала найти радиус. Напомним, площадь круга мы находим, умножая число пи на квадрат радиуса. Если мы площадь разделим на число пи, а потом извлечём корень квадратный из результата, это и будет радиус. Остаётся только умножить его на два – и мы получим диаметр.
Дюймы против мм. Откуда путаница и когда необходима таблица соответствия
Трубы, диаметр которых обозначается дюймами (1″, 2″
) и/или долями дюймов (1/2″, 3/4″
), являются общепринятым стандартом в водо – и водогазоснабжении.
Как правило монтаж дюймовых труб проходит без затруднений, но при их замене на трубы из пластика, меди и нержавеющей стали возникает проблема – несоответствие размера обозначенного дюйма (33,5 мм
) к его реальному размеру (25,4 мм
).
Обычно этот факт вызывает недоумение, но если глубже заглянуть в процессы происходящие в трубе, то логика несоответствия размеров становится очевидна и непрофессионалу. Все довольно просто – читайте дальше.
Дело в том, что при создании водного потока ключевую роль играет не внешний, а внутренний диаметр и по этой причине для обозначения используется именно он.
Однако несоответствие обозначаемых и метрических дюймов все равно остается, т. к. внутренний диаметр стандартной трубы составляет 27,1 мм
, а усиленной – 25,5 мм
. Последнее значение стоит довольно близко к равенству 1″”=25,4
но все же им не является.
Разгадка состоит в том, что для обозначения размера труб применяется номинальный, округленный до стандартного значения диаметр (условный проход Dy
). Величина условного прохода подбирается так, чтобы пропускная способность трубопровода увеличивалась от 40 до 60%
в зависимости от роста величины индекса.
В ситуациях с пластиковыми трубами для решения проблемы несоответствующих размеров используются переходные элементы. При необходимости заменить или состыковать дюймовые трубы с трубами, выполненными по реальным метрическим размерам – из меди, нержавейки, алюминия, следует брать во внимания и наружный, и внутренний диаметры.
Таблица соответствия условного прохода дюймам
| Ду | Дюймы | Ду | Дюймы | Ду | Дюймы |
| 6 | 1/8″ | 150 | 6″ | 900 | 36″ |
| 8 | 1/4″ | 175 | 7″ | 1000 | 40″ |
| 10 | 3/8″ | 200 | 8″ | 1050 | 42″ |
| 15 | 1/2″ | 225 | 9″ | 1100 | 44″ |
| 20 | 3/4″ | 250 | 10″ | 1200 | 48″ |
| 25 | 1″ | 275 | 11″ | 1300 | 52″ |
| 32 | 1(1/4)” | 300 | 12″ | 1400 | 56″ |
| 40 | 1(1/2)” | 350 | 14″ | 1500 | 60″ |
| 50 | 2″ | 400 | 16″ | 1600 | 64″ |
| 65 | 2(1/2)” | 450 | 18″ | 1700 | 68″ |
| 80 | 3″ | 500 | 20″ | 1800 | 72″ |
| 90 | 3(1/2)” | 600 | 24″ | 1900 | 76″ |
| 100 | 4″ | 700 | 28″ | 2000 | 80″ |
| 125 | 5″ | 800 | 32″ | 2200 | 88″ |
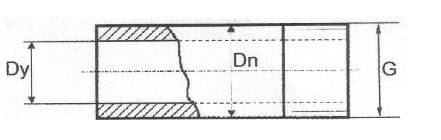
Таблица соответствия диаметра условного прохода, резьбы и наружных диаметров трубопровода в дюймах и мм.
Условный проход трубы Dy. мм | Диаметр резьбы G”. дюйм | Наружный диаметр трубы Dn. мм | ||
Трубы стапьные водо/водогазoпроводные ГОСТ 3263-75 | Трубы стальные эпектросварные прямошовные ГОСТ 10704-91. Трубы стальные бесшовные горячедеформированные ГОСТ 8732-78. ГОСТ 8731-74 (ОТ 20 ДО 530 мл) | Полимерная труба. ПЭ, ПП, ПВХ | ||
ГОСТ
– государственый стандарт, используемый в тепло – газо – нефте – трубопроводах
ISO
– стандарт обозанчения диаметров, используется в сантехнических инженерных системах
SMS
– шведский стандарт диаметров труб и запорной арматуры
DIN / EN
– основной евросортамент для стальных труб по DIN2448 / DIN2458
ДУ (Dy)
– условный проход
Таблицы с размерами полипропиленовых труб представлены в следующей статье >>>
Таблица соответствия условного диаметра труб с международной маркировкой
| ГОСТ | ISO дюйм | ISO мм | SMS мм | DIN мм | ДУ |
| 8 | 1/8 | 10,30 | 5 | ||
| 10 | 1/4 | 13,70 | 6,35 | 8 | |
| 12 | 3/8 | 17,20 | 9,54 | 12,00 | 10 |
| 18 | 1/2 | 21,30 | 12,70 | 18,00 | 15 |
| 25 | 3/4 | 26,90 | 19,05 | 23(23) | 20 |
| 32 | 1 | 33,70 | 25,00 | 28,00 | 25 |
| 38 | 1 ¼ | 42,40 | 31,75 | 34(35) | 32 |
| 45 | 1 ½ | 48,30 | 38,00 | 40,43 | 40 |
| 57 | 2 | 60,30 | 50,80 | 52,53 | 50 |
| 76 | 2 ½ | 76,10 | 63,50 | 70,00 | 65 |
| 89 | 3 | 88,90 | 76,10 | 84,85 | 80 |
| 108 | 4 | 114,30 | 101,60 | 104,00 | 100 |
| 133 | 5 | 139,70 | 129,00 | 129,00 | 125 |
| 159 | 6 | 168,30 | 154,00 | 154,00 | 150 |
| 219 | 8 | 219,00 | 204,00 | 204,00 | 200 |
| 273 | 10 | 273,00 | 254,00 | 254,00 | 250 |
Диаметры и другие характеристики трубы из нержавеющей стали
| Проход, мм | Диаметр наружн., мм | Толщина стенок, мм | Масса 1 м трубы (кг) | ||
| стандартных | усиленных | стандартных | усиленных | ||
| 10 | 17 | 2.2 | 2.8 | 0.61 | 0.74 |
| 15 | 21.3 | 2.8 | 3.2 | 1.28 | 1.43 |
| 20 | 26.8 | 2.8 | 3.2 | 1.66 | 1.86 |
| 25 | 33.5 | 3.2 | 4 | 2.39 | 2.91 |
| 32 | 42.3 | 3.2 | 4 | 3.09 | 3.78 |
| 40 | 48 | 3.5 | 4 | 3.84 | 4.34 |
| 50 | 60 | 3.5 | 4.5 | 4.88 | 6.16 |
| 65 | 75.5 | 4 | 4.5 | 7.05 | 7.88 |
| 80 | 88.5 | 4 | 4.5 | 8.34 | 9.32 |
| 100 | 114 | 4.5 | 5 | 12.15 | 13.44 |
| 125 | 140 | 4.5 | 5.5 | 15.04 | 18.24 |
| 150 | 165 | 4.5 | 5.5 | 17.81 | 21.63 |
Радиусы и диаметры на чертеже по ГОСТу
Традиционно, в пояснительных записках и на чертежах используется условное обозначение радиуса латинской буквой R. После этого символа идет размерное число.
Отрезок начинается от центра окружности, на конце отрезка рисуется стрелка, направленная к самой окружности.
Бывают случаи, когда значение радиуса велико и поэтому линию приближают к дуге и показывают с изломом под 90 градусов.
Также зачастую исполнителю нет необходимости показывать центр окружности, особенно если размер очень большой и составляет несколько метров, поэтому сам отрезок не доводят до центра.
Рисунок 2. Радиусы и диаметры на чертеже по ГОСТу
Дуга окружности
Дугу можно измерять не только в единицах измерения длины, но и в градусах. Вся дуга окружности имеет градусную меру 360\(\circ\). Тогда половина дуги окружности будет равняться 180.
При этом дуга, равная 180\(\circ\), называется полуокружностью. Полуокружность ограничивается двумя концами диаметра.
Думаем, хоть раз в жизни вы слышали фразу “повернуться на 180\(\circ\) градусов” или “поменять свое мнение на 180\(\circ\) градусов”. Это означает, что человек меняет свое мнение буквально на противоположное. Рассмотрим на примере окружности: пусть человек стоит в точке А. Ему нужно пройти по окружности ровно 180\(\circ\).
Поскольку человеку нужно пройти полуокружность, то она ограничивается диаметром. Достроим диаметр АВ, тогда наш человек окажется в точке В, то есть на противоположной стороне окружности.
А если он дважды пройдет полуокружность, то снова окажется в точке А, то есть пройдет дугу в 2 * 180 = 360 градусов.
Поэтому если человек будет находиться в точке О и захочет повернуться на 180 градусов, то вместо точки А он будет смотреть на точку В. При повороте на 360 градусов, человек снова будет смотреть на точку А.
| Почему если мы хотим что-то сильно поменять, то лучше разворачивать жизнь на 180 градусов, а не на 360? При повороте на 180 градусов, мы смотрим на что-то с совершенно противоположной стороны. А вот если повернуться на 360 градусов, то мы будем смотреть на ту же точку, на которую смотрели изначально. |
Как показать несколько радиусов на чертеже
Если из одного центра проводятся несколько радиусов, то согласно принятой практике для простоты прочтения чертежа их не располагают на одной прямой, между ними должен быть угол.
Если необходимо показать несколько линий радиуса, то до центра доводят только крайние радиусы, а остальные остаются укороченными.
В ситуациях, когда применяется большое количество одинаковых радиусов скругления, наносить размеры и показывать условные обозначения не обязательно. В примечаниях указывают всю необходимую информацию, к примеру, что «радиусы скругления составляют 10 мм» или «неуказанные радиусы 7 мм».
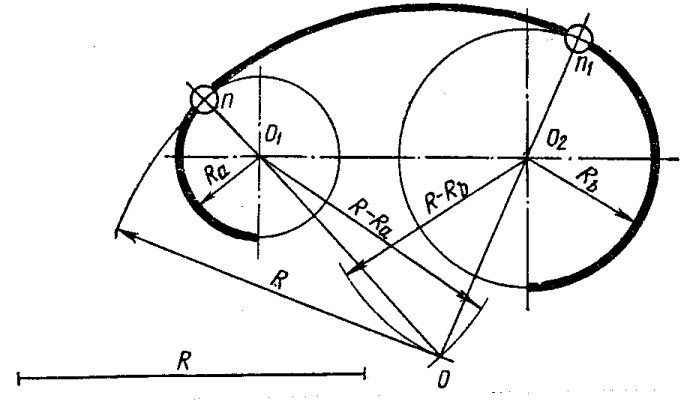Рисунок 4. Несколько радиусов на чертеже
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две – А и В – можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
В пределах окружности имеются точки Х такие
, что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
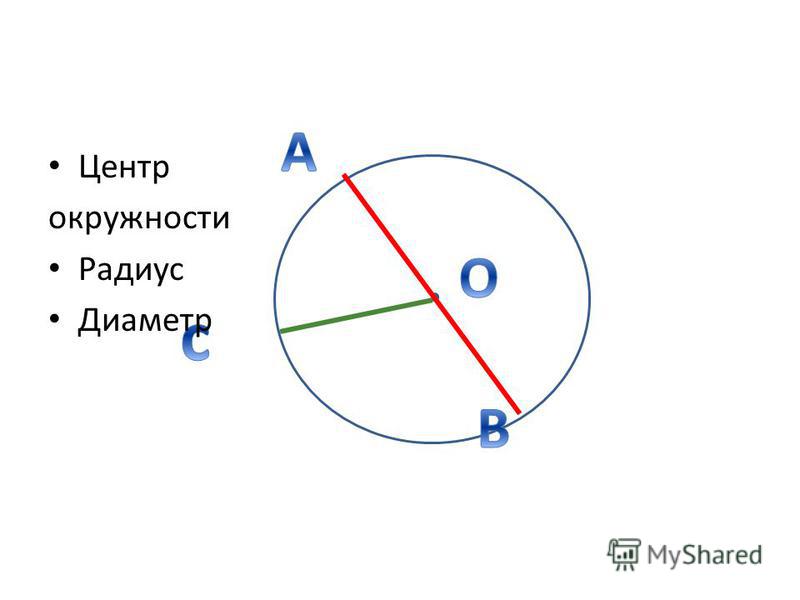
Основные термины окружности
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры – это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр – расстояние между точками
, проходящее через центр фигуры.
Вычисление диаметра окружности из чертежа окружности
- Внутри окружности начертите горизонтальную прямую, проходящую от одной точки окружности к другой.Для этого воспользуйтесь линейкой или угольником. Прямая может проходить в верхней части круга, в нижней, или где-нибудь посередине.
- Пометьте точки, в которых прямая пересекает окружность, буквами «A» и «B.»
- Начертите две пересекающиеся окружности, одну – с центром в точке A, а другую – с центром в точке B.Убедитесь, что две окружности пересекаются так, будто образуют диаграмму Венна.
- Через две точки, в которых окружности пересеклись, проведите прямую.Отрезок этой прямой между двумя точками и будет равен диаметру окружности.
- Измерьте диаметр.Измерьте его с помощью линейки, а если нужна большая точность – штангенциркулем с цифровой индикацией. Готово!
Ответы на вопросы
В каком случае допускается не показывать радиус?
Радиус не показывают, если размер скругления в масштабе чертежа равен или менее 1 мм.
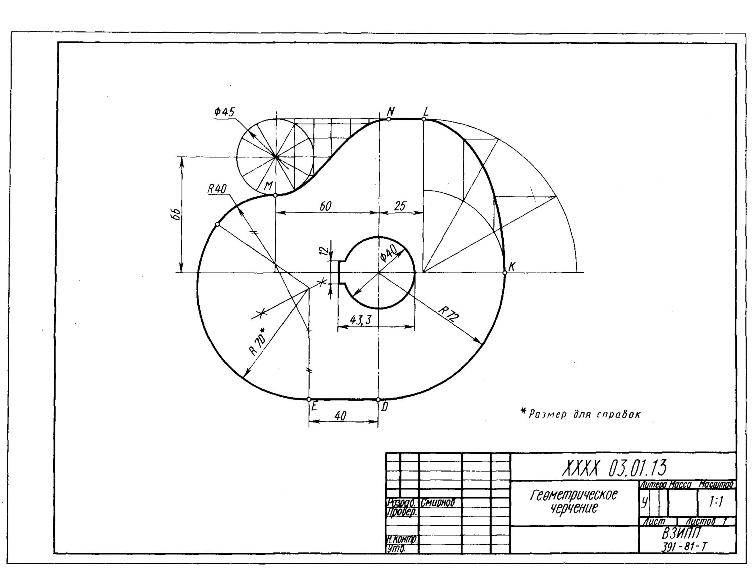Рисунок 7. Пример обозначения радиусов на чертеже
Как можно упростить обозначение одинаковых радиусов?
Зачастую детали выполняются симметричными, и их скругления имеют одинаковые значения. В этом случае обозначается стрелка для каждого скругления, но все они имеют общую полку, на которой выполняется простановка размерного числа.
Рисунок 8. Одинаковые радиусы
Нужно ли писать единицу измерения после обозначения радиуса?
Радиус, так же, как и ширина, толщина, длина или высота изделия относится к линейным размерам. Согласно требованиям ГОСТа, по умолчанию их наносят в миллиметрах. Соответственно других единицы измерения указывают, если размер определяется в метрах, сантиметрах, дециметрах, футах или иных единицах.
Выводы
Круг – плоская, двухмерная фигура. Шар – объемное трехмерное геометрическое тело. Тем не менее, они имеют массу сходств (наличие ограничивающей поверхности, диметра и радиуса, наполненность структуры в отличие от той же окружности, возможност вычислить площадь).
Чем же отличается круг от шара? Круг плоский, шар же имеет объем. Именно объемность шара позволяет ему делиться на сечения, которые по своей сути являются кругами. Круг, напротив, делится на сектора.
Публикации по теме:
Детско-родительский игровой сеанс «Круг» для детей ОВЗ Игровое занятие КРУГ для детей ОВЗ Тема «Осень. Природные явления» Цели и задачи занятия КРУГ Главная цель занятия КРУГ – дать каждому ребенку.
Конкурс профессионального мастерства «Солнечный круг» (фотоотчет) С 12 по 26 октября 2015 года в нашем детском саду проходил конкурс профессионального мастерства «Воспитатель года». Цель конкурса: выявление.
Конспект НОД по ФЭМП «Знакомьтесь: круг» Конспект НОД по ФЭМП во второй младшей группе «Знакомьтесь- круг» Цель: развитие познавательных интересов детей Задачи: Познакомить.
НОД по математике «Круг и квадрат» (младшая группа) Тема: «Круг и квадрат» (младшая группа) Образовательная область: познание Цель: Продолжать учить находить один и много предметов в специально.
Поделки в технике «объемный квиллинг» Здравствуйте, коллеги! Недавно открыла для себя технику объемного квиллинга. Искусство, которое на русском языке называют «бумагокручением»,.
Проект по математическому развитию «Круг, квадрат и треугольник-фигуры важные, фигуры нужные» Номинация проекта – «Дошкольный возраст» Вид проекта: долгосрочный, фронтальный. Участники проекта: подгруппа детей средней группы, воспитатель.
«Снежинка 3-D». Объемный модуль для украшения интерьера Приближаются Новогодние праздники и перед нами, как воспитателями опять стоит вопрос «Чем же удивить детей и взрослых?». Просторы Интернета.
Совместная образовательная деятельность по ФЭМП «Круг и квадрат» Совместная образовательная деятельность взрослого и детей ФЭМП «Круг и квадрат». Цель: закреплять умение различать и называть круг и квадрат.
Весенний объемный тюльпан на открытке в подарок маме Не за горами прекрасный весенний праздник 8 Марта. И уже сейчас многие педагоги задумались над тем, что бы смастерить с детьми мамам в.
На уроках геометрии в школе все мы изучали свойства различных фигур и линий. Каждая из них имеет свои особенности, а порой некоторые из них взаимосвязаны друг с другом. Взять для примера хотя бы круг и окружность – между ними есть определенная связующая линия. Только вот какая? Давайте вместе разберемся в этом вопросе.Окружность
представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности. Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность. Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится. По этой причине имеется четкое понятие, что окружность делит всю плоскость на две части – внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, поскольку плоскость в общем понимании не имеет границ.Круг
является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность. Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.
Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии. Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга. Иными словами, круг представляет собой не только окружность, которая является его границей, но также и то бесконечное число точек, находящихся внутри этой окружности.
Выводы сайт
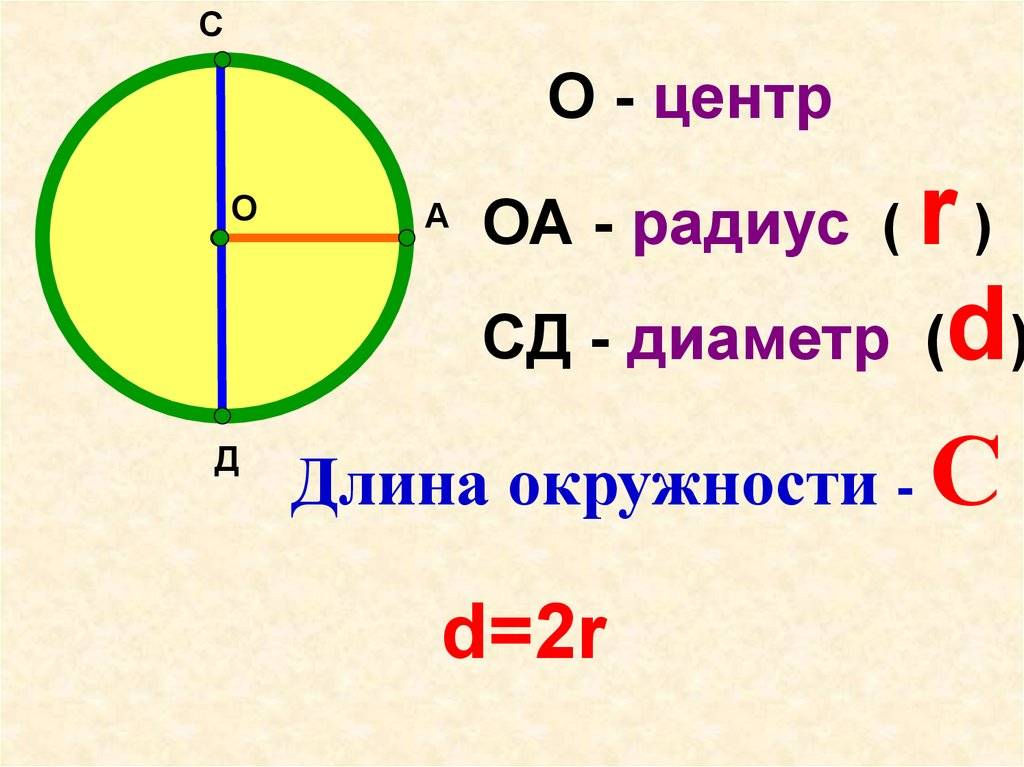
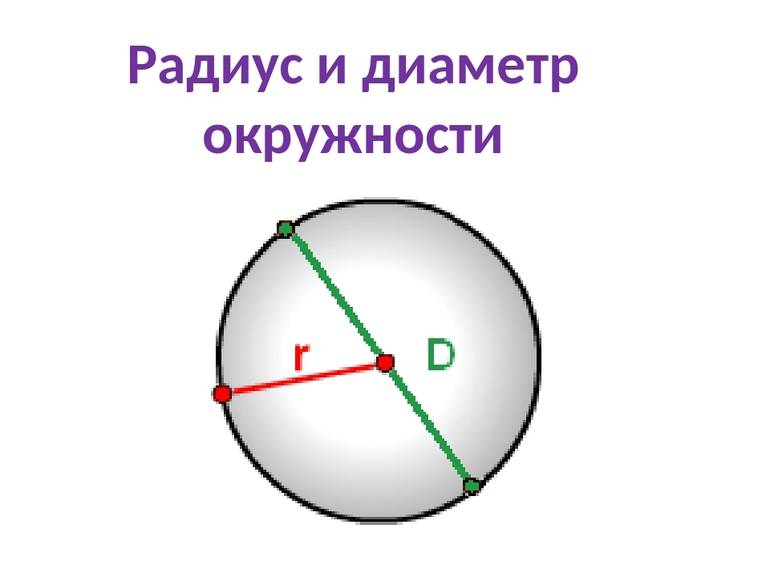
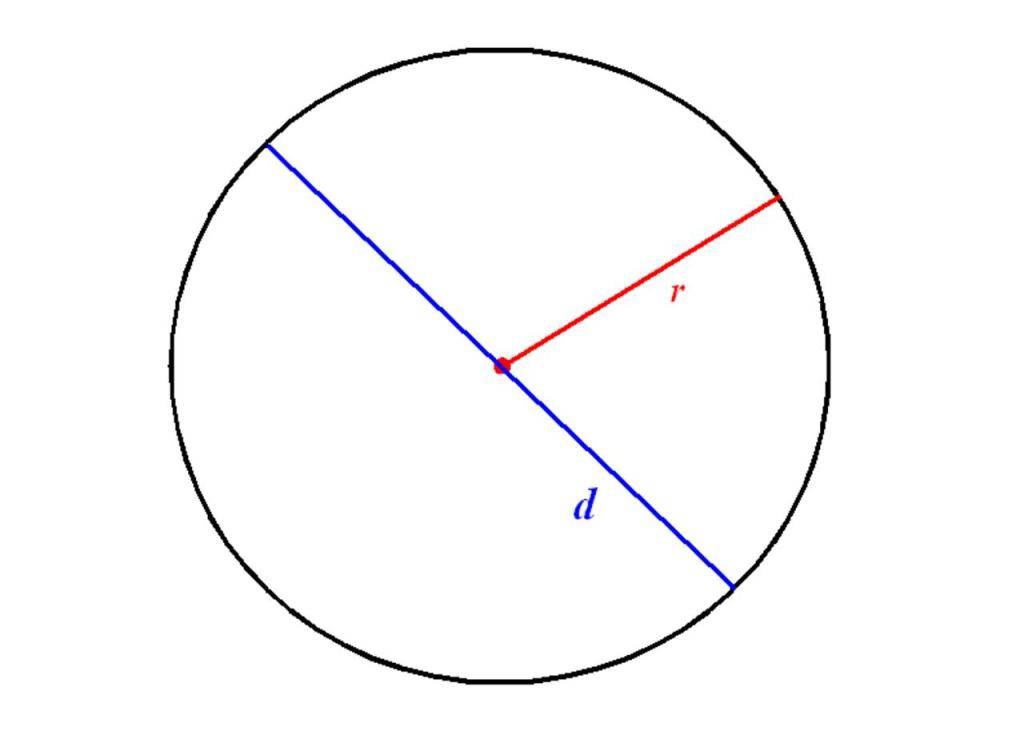
- Диаметр всегда равняется удвоенному радиусу окружности.
- Радиус окружности равен половине диаметра этой окружности. R = D/2
Сначала разберемся в отличии между кругом и окружностью. Чтобы увидеть эту разницу, достаточно рассмотреть, чем являются обе фигуры. Это бесчисленное количество точек плоскости, располагающиеся на равном расстоянии от единственной центральной точки. Но, если круг состоит и из внутреннего пространства, то окружности оно не принадлежит. Получается, что круг это и окружность, ограничивающая его (о-кру(г)жность), и бесчисленное число точек, что внутри окружности.
Для любой точки L
, лежащей на окружности, действует равенство OL=R
. (Длина отрезка OL
равняется радиусу окружности).
Отрезок, который соединяет две точки окружности, является ее хордой
.
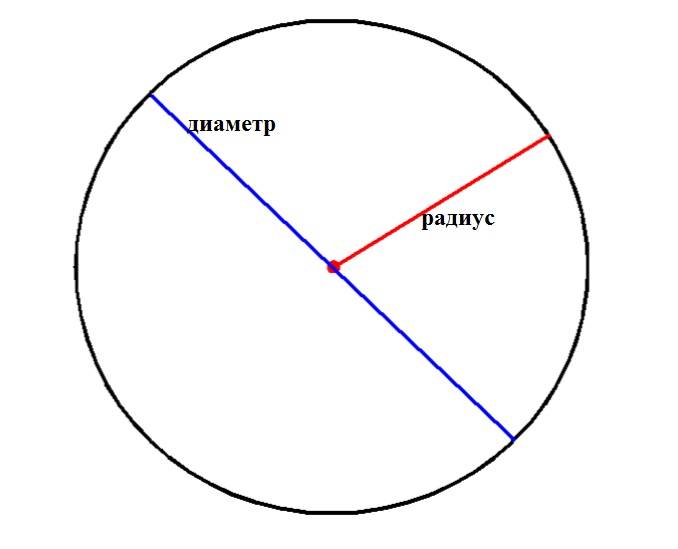
Хорда, проходящая прямо через центр окружности, является диаметром
этой окружности (D)
. Диаметр можно вычислить по формуле: D=2R
Длина окружности
вычисляется по формуле: C=2\pi R
Площадь круга
: S=\pi R^{2}
Дугой окружности
называется та ее часть, которая располагается между двух ее точек. Эти две точки и определяют две дуги окружности. Хорда CD
стягивает две дуги: CMD
и CLD
. Одинаковые хорды стягивают одинаковые дуги.
Центральным углом
называется такой угол, который находится между двух радиусов.
Длину дуги
можно найти по формуле:
Используя градусную меру: CD = \frac{\pi R \alpha ^{\circ}}{180^{\circ}}
- Используя радианную меру: CD = \alpha R
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
В случае, если хорды AB
и CD
окружности имеют пересечение в точке N
, то произведения отрезков хорд, разделенные точкой N
, равны между собой.
AN\cdot NB = CN \cdot ND
