В чем заключаются основные отличия между окружностью и кругом: краткое пояснение

Центр

Центр круга имеет множество свойств и функций. Вот несколько из них:

Свойство	Описание
Координаты	Центр круга можно определить с помощью его координат — пары чисел (x, y), где x — горизонтальная координата и y — вертикальная координата.
Радиус	Центр круга также определяет его радиус — расстояние от центра до любой точки на окружности.
Симметрия	Центр круга является центром симметрии для всех точек на окружности. Это означает, что если вы отразите круг относительно его центра, он останется неизменным.

Важно отметить, что центр круга может быть расположен в любом месте. Таким образом, он может быть смещен относительно центра координатной системы или относительно других объектов

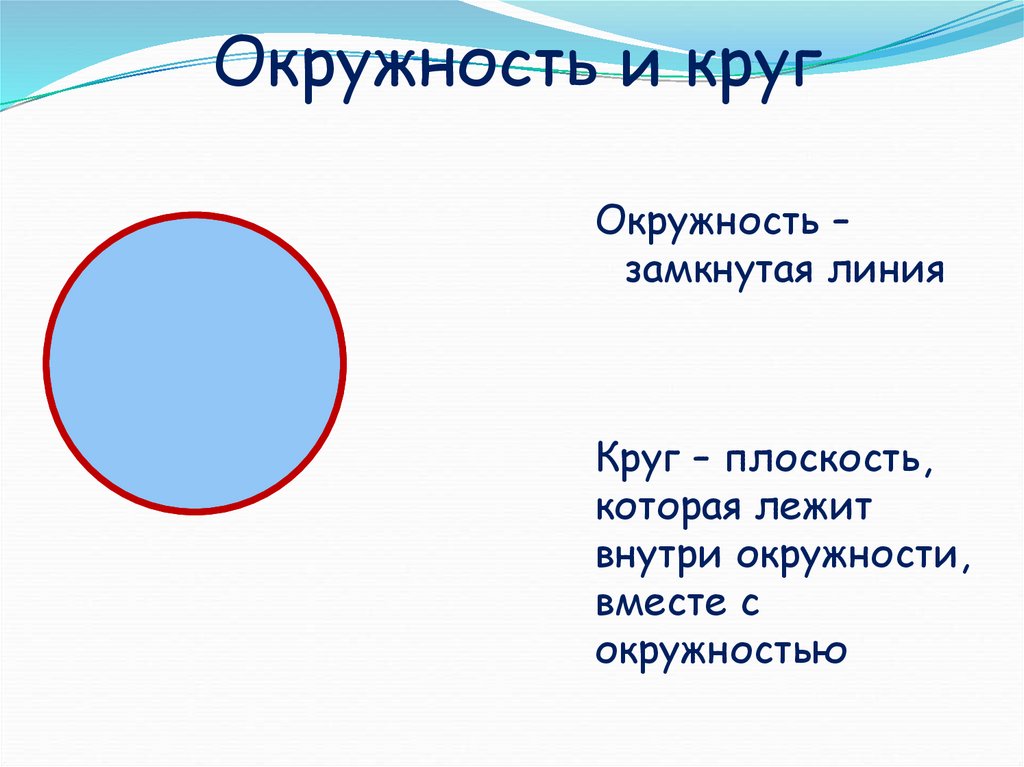
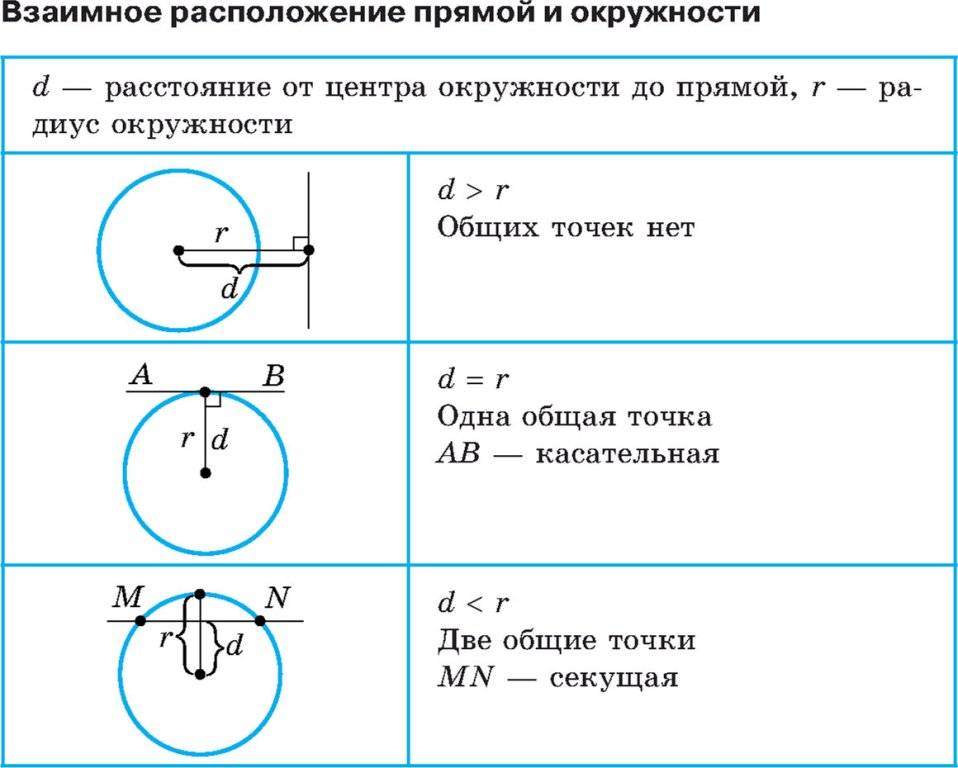
Окружность — это геометрическое место точек

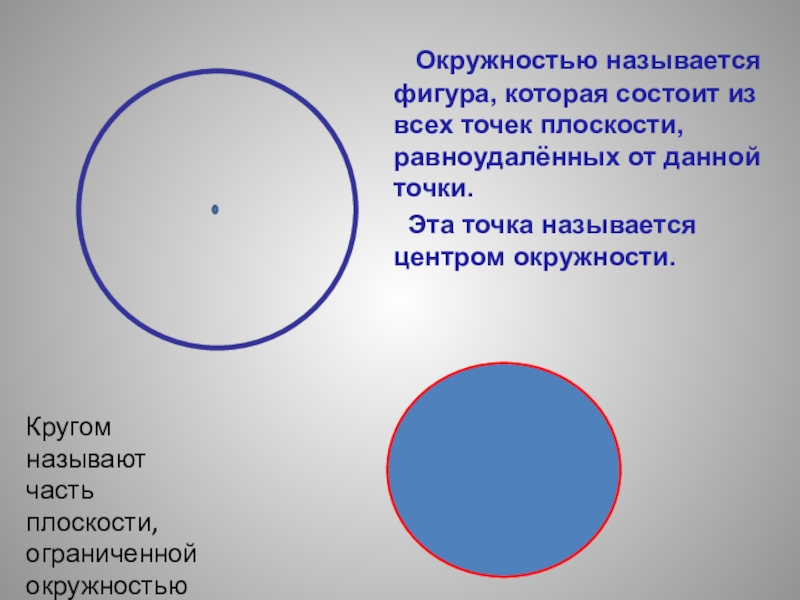
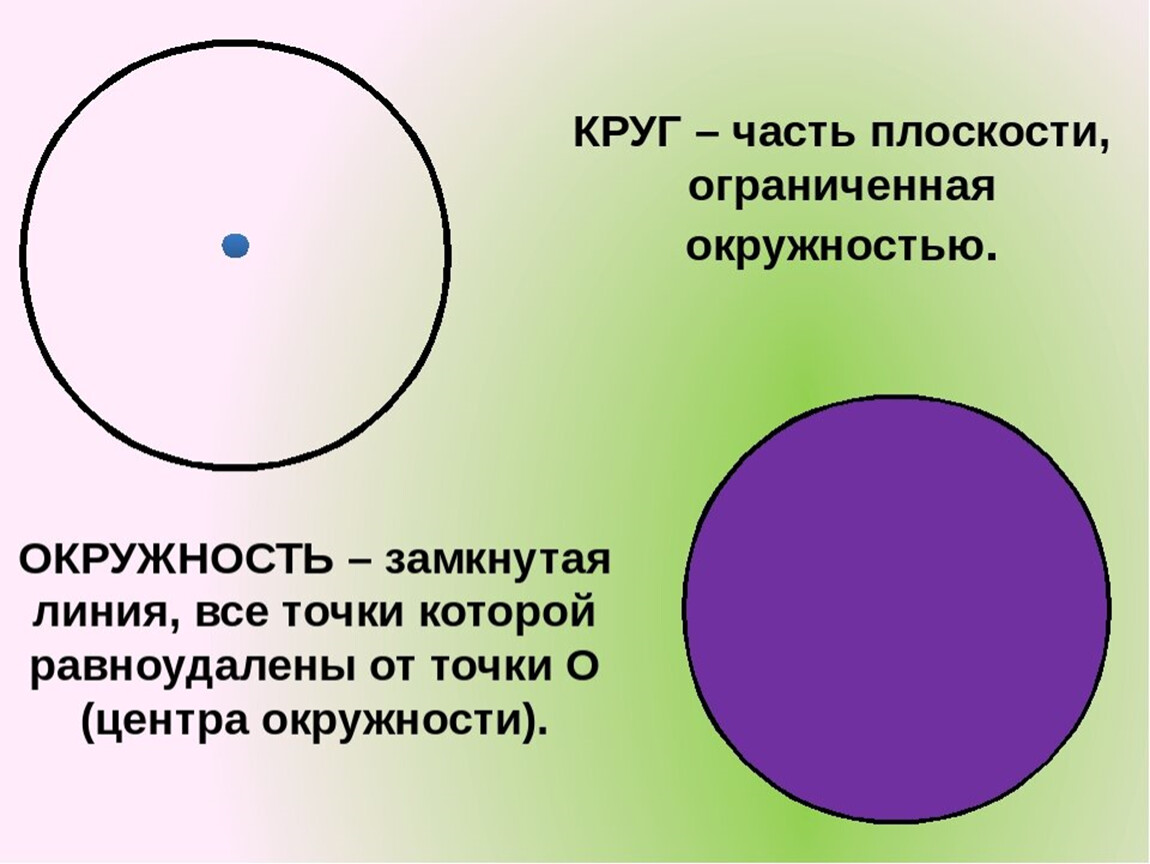
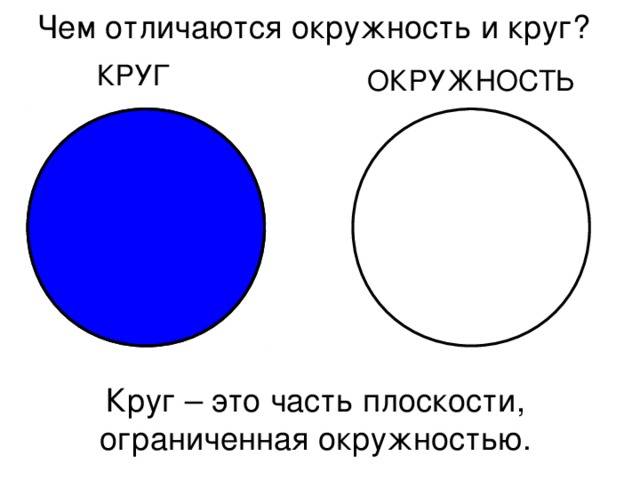
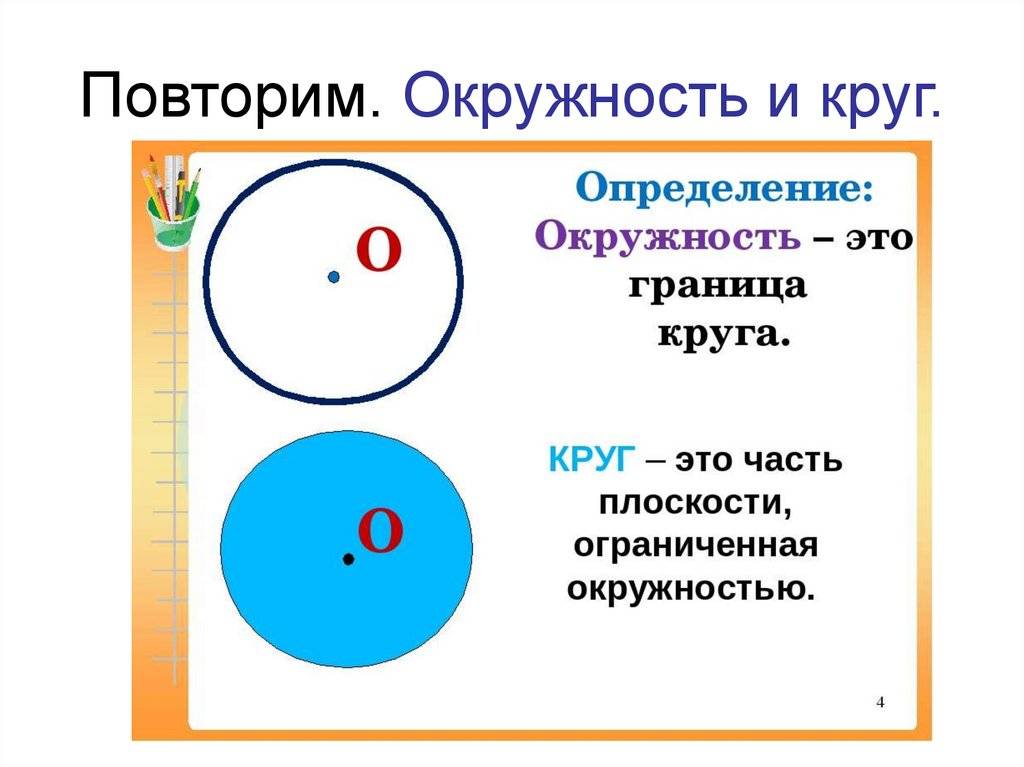
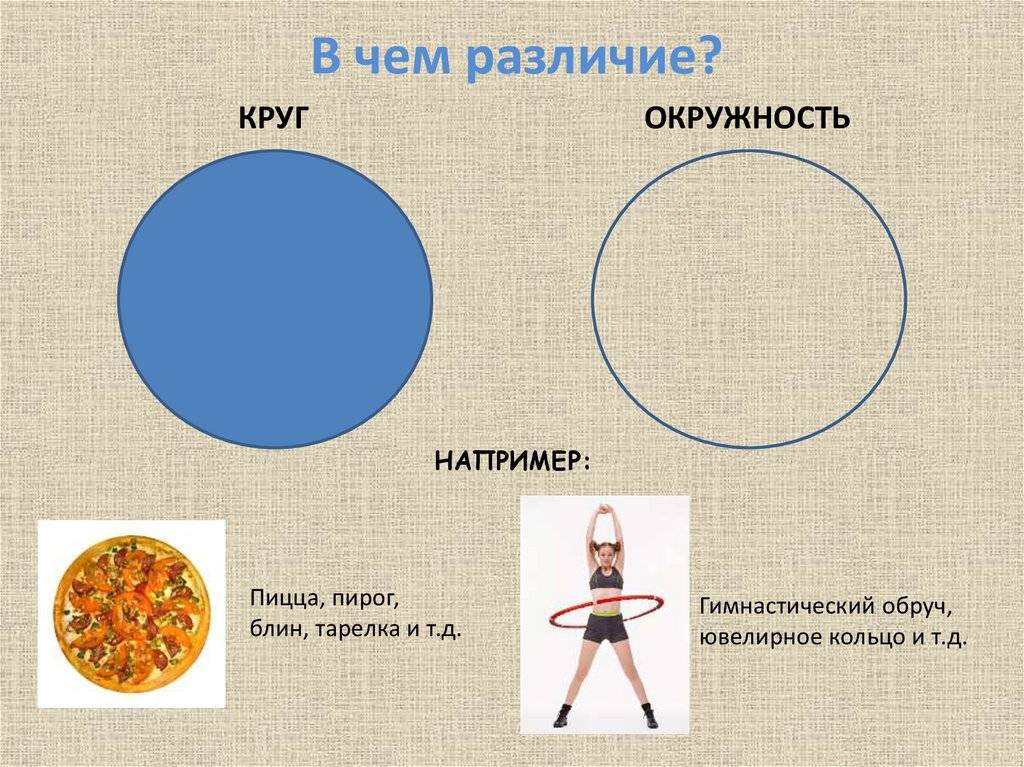
Важно отличать окружность от круга. Окружность — это граница круга, то есть его контур, в то время как круг — это сама фигура, заключенная внутри окружности

Другими словами, окружность — это линия, а круг — это площадь.

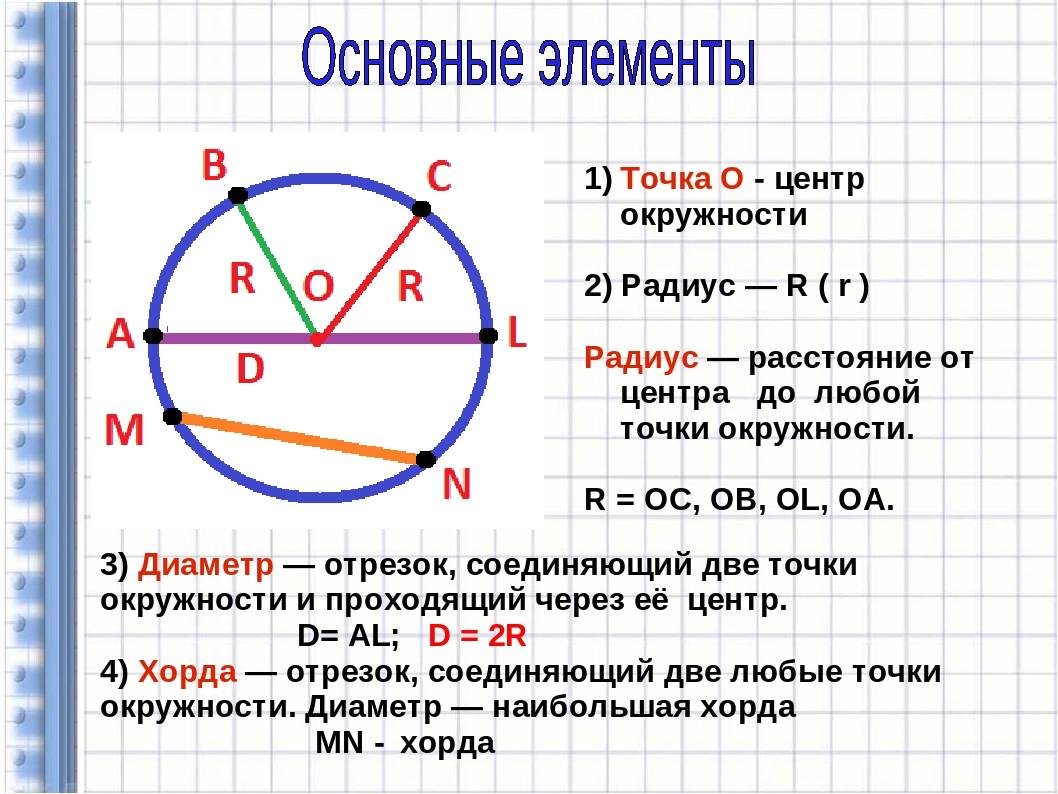
Центр окружности обозначается буквой «O», а расстояние от центра до любой точки на окружности называется радиусом окружности и обозначается буквой «r».

Окружность имеет множество свойств и особенностей, которые используются в различных областях науки и техники. Например, окружность используется в геометрии, физике, инженерии и даже в компьютерной графике для создания кривых и округлых форм.

Важно помнить:

— Окружность состоит из всех точек, равноудаленных от центра.

— Центр окружности обозначается буквой «O».

— Расстояние от центра до любой точки на окружности называется радиусом и обозначается буквой «r».

— Окружность — это граница круга, а круг — это фигура, заключенная внутри окружности.

Интуитивно понимать окружность легко: подумайте о кругах, которые образуют планеты, колеса автомобилей или диски компакт-дисков

Все они являются примерами окружностей и демонстрируют ее важность и применимость в повседневной жизни

ImGist определил, что разница между кругом и окружностью заключается в следующем:

Окружность является лишь частью круга, его границей, в то время как круг является более обширной и полноценной фигурой;
Окружность – это кривая линия, состоящая из бесчисленного множества точек, равноудаленных от центра, а круг представляет собой не только сумму этих точек окружности, но также и все те точки, которые расположены внутри этой самой окружности.

Окружность
– это огромное количество точек на плоскости, равноудаленных от некой точки этой же плоскости, именуемой центром окружности. Окружность представляет собой замкнутую кривую, лежащую от центра на фиксированном расстоянии, нарываемом радиусом окружности.

Круг
– это огромное количество точек плоскости, удаленных от некой точки этой же плоскости, именуемой центром круга, на расстояние, не превышающеей определенной величины, именуемой радиусом круга. Круг представляет собой сплошную фигуру, включающую окружность и все точки, лежащие в ней.

Следовательно, круг – это участок плоскости, а окружность – черта этого участка. Потому есть возможность говорить о площади круга и длине окружности, однако неправильно говорить о длине круга и площади окружности.

Так как точки окружности удалены от центра на расстояние, не превышающее радиуса, то они все принадлежат кругу. Другими словами, окружность принадлежит кругу, который она ограничивает. В особых случаях может рассматриваться круг в отсутствие границы – огромное количество точек круга, не принадлежащих его границе (окружности).

Окружность разделяет плоскость на две части – лежащую снутри и лежащую снаружи. Попрасть из одной части в другую нереально в отсутствие скрещения окружности. Площаль внутренней части конечна, площадь наружной части нескончаема.

Центр окружности не принадлежит окружности (кроме вырожденного варианта окружности нулевого радиуса). Центр круга всегда принадлежит кругу, т.к. находится снутри ограничивающей его окружности.

openclass.ru – методическая разработка «Окружность и круг»
otvet.mail.ru – чем отличается круг от окружности?

NMitra
В Opera есть баг: у вложенного элемента углы не закругляются. Это можно подправить, дописав

#ball:after {content: “”;position: absolute;top: 0; bottom: 0; right: 0; left: 0;box-shadow: 0 0 0 100px #fff;border-radius: 100%; }

Но тогда тень в Гугл Хром “обрезанная” получается. Поскольку Опера переезжает на движок Google, то я сделала выбор в пользу его браузера.
Космо Мизраил
Прикольно.Сейчас делаю дизайн как раз с планетами, но аватарки и другие изображения приходится делать плоскими, потому что img не применишь box-shadow: inset.
NMitra
Сделайте фоном background. Скоро благодаря поддержки трансформации CSS можно будет добавлять объём. Предвестники http://codepen.io/html5web/pen/pnbwo
Космо Мизраил
Мдо, вроде-бы для вебкита, а не работает х) Это будет вступать лет пять ещё, до этого надо ещё дожить

Фоны сделать не всегда получится, а вот наложить поверх изображения элемент с заданными стилями очень даже можно. Но это если известны размеры изображения.Пример: http://jsfiddle.net/9qzm6/

Ещё нашёл скрипт, который выполняет эту работу самостоятельно:http://www.htmldrive.net/items/demo/1156/Multiple-CSS3-Image-StylesЗдесь он сам определяет размер, если изображение загрузилось. Нужен jQuery.

Это так, на заметку
NMitra
Там нужны настройки какие-то устанавливать.. Это сильно вперёд:))

Пжалст я ваш постоянный читатель уже год как минимум
Анонимный
IE 11Все анимировано))
NMitra
Молодцом IE, дотянулось. Осталась Хрому убрать -webkit-, он теперь в числе отстающих.

Круг

Окружность — это фигура, которая представляет собой замкнутую кривую линию, состоящую из всех точек, равноудаленных от данной точки, называемой центром окружности.

Форма круга является симметричной и имеет бесконечное количество осей симметрии.

Радиус круга представляет собой расстояние от мидпоинта окружности до ее центра.

Диаметр круга — это отрезок, который соединяет две противоположные точки на окружности, проходящий через ее центр.

Площадь круга — это количество площади, занимаемое кругом на плоскости. Она вычисляется по формуле: S = πr², где π — постоянное число, равное приблизительно 3.14159, r — радиус круга.

Круг является одной из основных фигур в геометрии и имеет множество применений в различных областях науки и практической деятельности.

Определение и свойства

У окружности есть несколько важных характеристик. Радиус — это расстояние от центра окружности до любой её точки. Окружность также имеет диаметр — это отрезок, соединяющий две противоположные точки на окружности, проходящие через её центр. Диаметр равен удвоенному значению радиуса.

Площадь круга — это количество плоскости, которое содержится внутри его границы. Она вычисляется по формуле:

S = π * r^2.

где S — площадь круга, π (пи) — математическая константа, примерное значение которой равно 3,14, r — радиус круга.

Формула круга

Для определения площади круга используется формула:

Найдите диаметр круга, который представляет собой отрезок, соединяющий две точки на окружности и проходящий через центр.
Разделите диаметр пополам, чтобы найти радиус, который является расстоянием от центра до любой точки на окружности.
Возведите радиус в квадрат.
Умножьте полученное значение на число Пи (π), которое приближенно равно 3,14159.
Полученное произведение и будет площадью круга.

Формула площади круга:

S = π * r2

Где:

S — площадь круга;
π (Пи) — математическая константа, приближенно равная 3,14159;
r — радиус окружности.

Используя формулу площади круга, можно вычислить его территорию, то есть площадь, занимаемую кругом.

Примеры использования

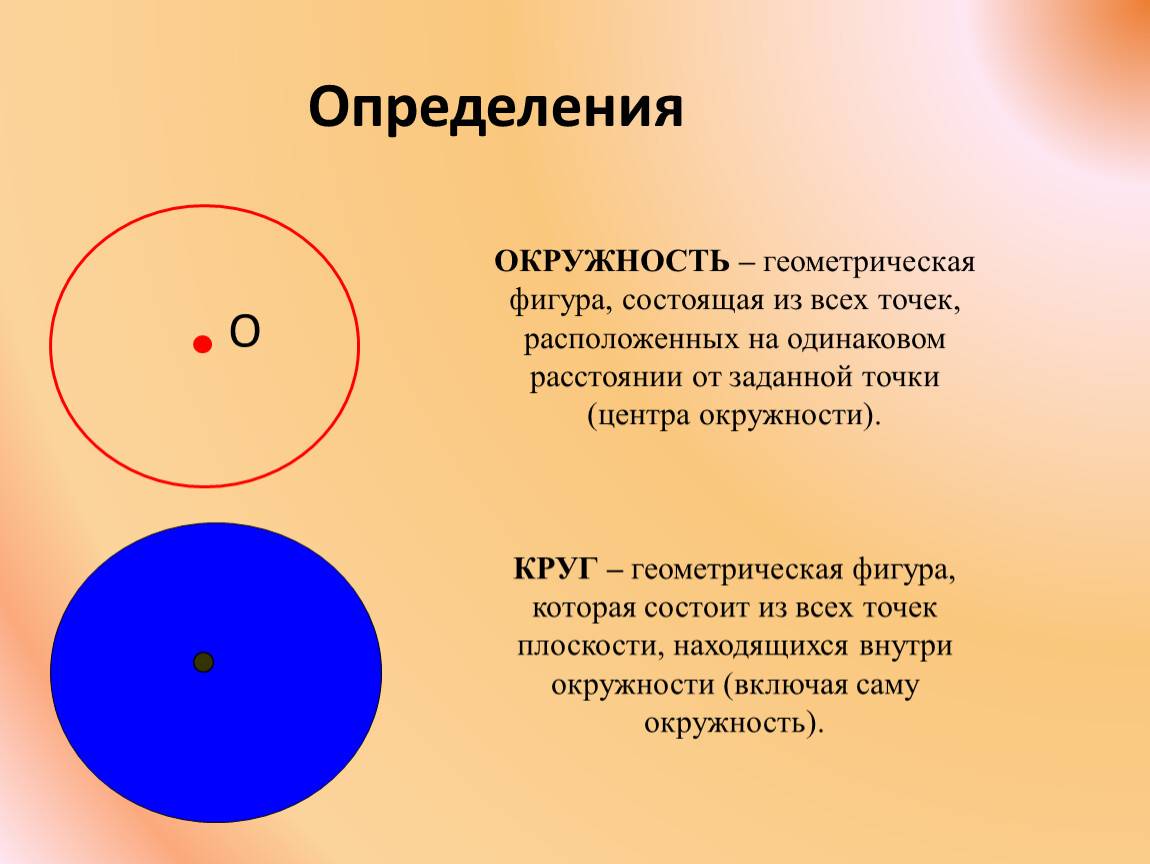
Окружность — это геометрическая фигура, состоящая из всех точек плоскости, которые находятся на одинаковом расстоянии от заданной точки. Диаметр окружности — это отрезок, соединяющий две точки на окружности и проходящий через ее центр. По своей форме окружность представляет собой замкнутую кривую с одной границей.

Круг — это геометрическая фигура, образованная всеми точками плоскости, которые находятся на определенном расстоянии от заданной точки, и сама эта точка — центр круга. Также круг определяется его радиусом, который является расстоянием от центра до любой точки на окружности. Круг представляет собой фигуру, ограниченную окружностью. Территория, заключенная внутри круга, называется площадью круга.

Примеры использования окружности и круга можно найти во многих областях жизни. Например, в архитектуре использование окружностей и кругов позволяет создавать красивые и эстетически приятные формы зданий и сооружений. В инженерии они применяются для создания колес и шестерен, а также для моделирования движений и процессов. В географии и картографии окружности используются для построения меридианов и параллелей на географических картах.

Понимание различий и применение окружностей и кругов помогает визуализировать и анализировать различные формы и границы, а также решать различные задачи в области геометрии и других наук.

Что такое круг?

Начертание круга начинается с окружности. Окружность – это замкнутая черта без конца и начала
, каждая точка которой находится на равном удалении от центра. Простейший пример окружности – гимнастический обруч.

Круг получится, если начертить окружность, например, на бумаге – и потом разукрасить ее. Любыми красками: желтой, синей, зеленой – какая больше нравится. Главное – заполнить чем-то пустоту. После окончания работы окружность превратится в фигуру, которую именуют кругом. Круг по сути своей – это некоторая часть двухмерной поверхности, закольцованная в окружность.

Круг обладает некоторыми важными для понимания его сущности параметрами. Кстати, часть данных параметров присуща и окружности.

Радиус
– расстояние от центральной точки круга или окружности до границы фигуры (линии, которая ее очерчивает).
Диаметр
– важная характеристика, которая так часто фигурирует в школьных заданиях. Это сумма двух радиусом, то есть расстояние между двумя противоположными точками на окружности.
Площадь
– свойство, характерное только для круга. Окружность не имеет его в силу своей структуры (потому что она пустая, а центр фигуры – воображаемая точка). В круге, напротив, несложно определить центр. Через центральную точку фигуры достаточно просто прочертить ряд линий, которые поделят круг на сектора.

Вписанная окружность

Окружность называетсявписанной в многоугольник, если она касается его сторон. Центр вписанной окружности лежит в точке пересечения биссектрис углов многоугольника.

Не во всякий многоугольник можно вписать окружность.

Площадь многоугольника, в который вписана окружность можно найти по формуле

здесь — полупериметр многоугольника, — радиус вписанной окружности.

Отсюда радиус вписанной окружности равен

Если в выпуклый четырехугольник вписана окружность, то суммы длин противоположных сторон равны. Обратно: если в выпуклом четырехугольнике суммы длин противоположных сторон равны, то в четырехугольник можно вписать окружность:

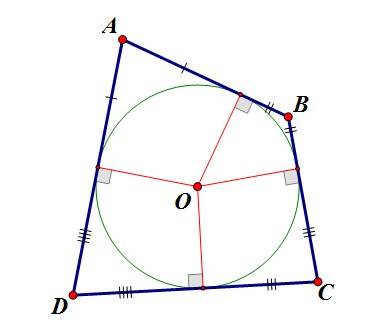
В любой треугольник можно вписать окружность, притом только одну. Центр вписанной окружности лежит в точке пересечения биссектрис внутренних углов треугольника.

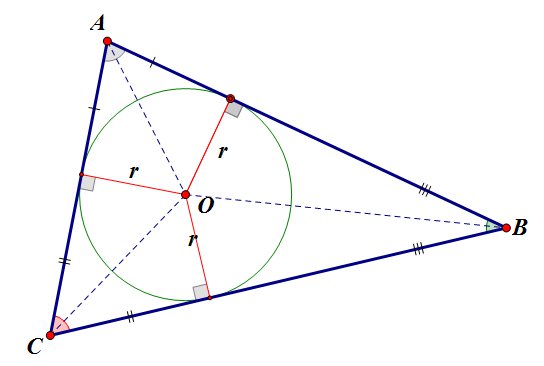
Радиус вписанной окружности равен
. Здесь

Углы в окружности

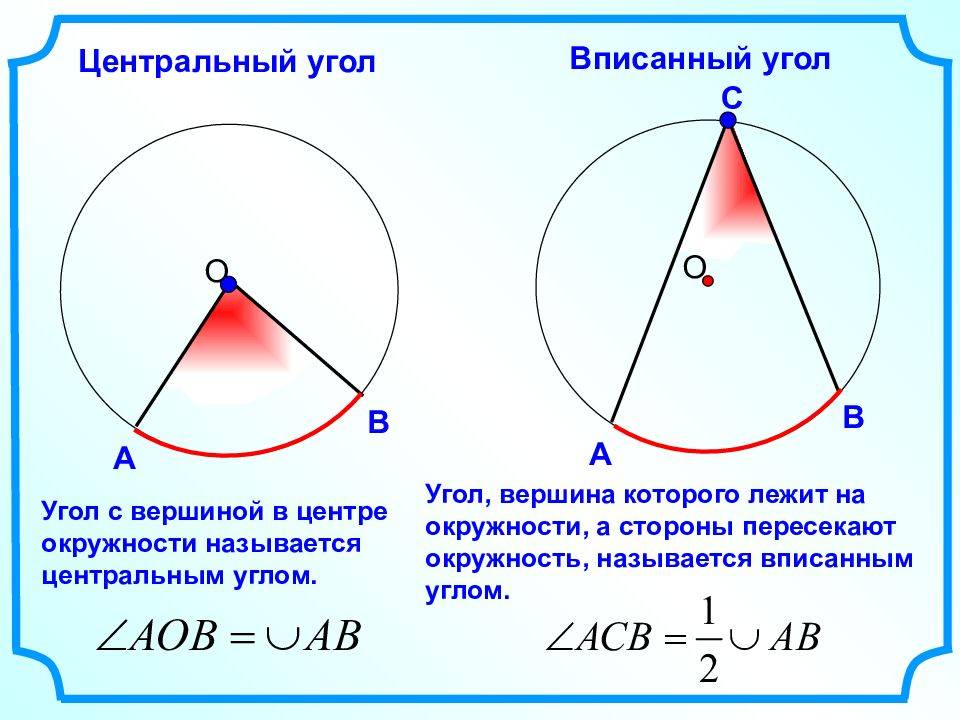
Центральный угол – это угол, вершина которого лежит в центре окружности. При этом угол опирается на дугу окружности.

На рисунке угол АОВ будет центральным.

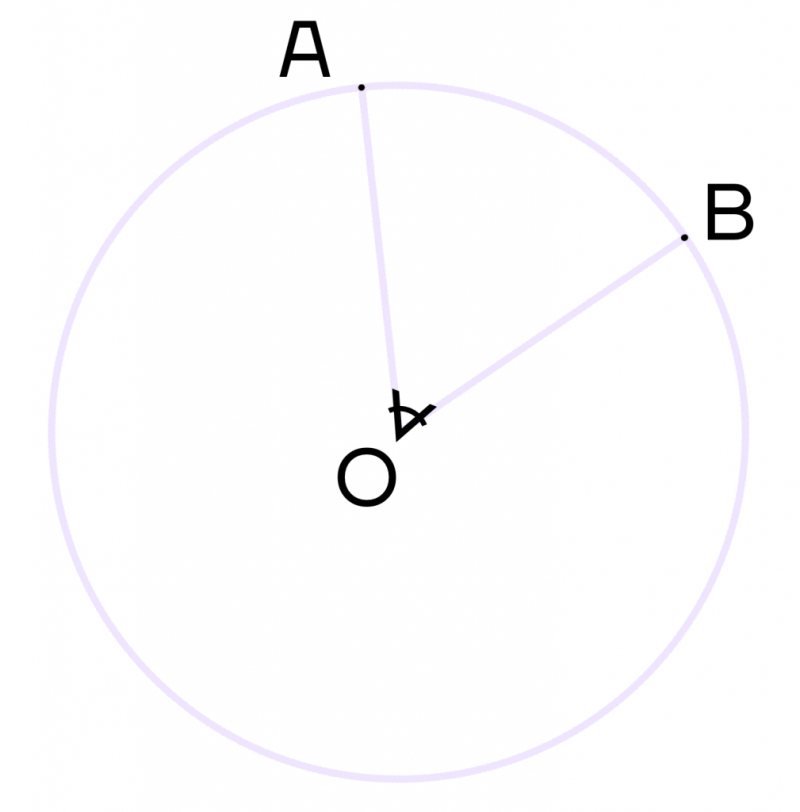
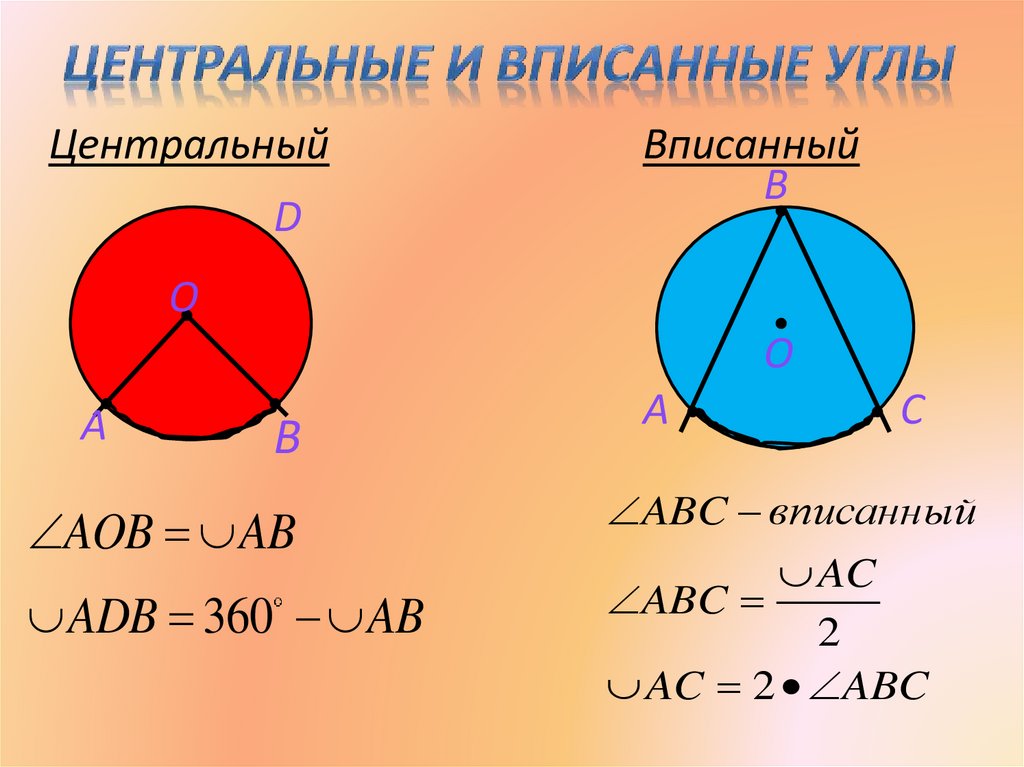
Свойство центрального угла:

Центральный угол равен градусной мере дуги, на которую он опирается.

Например, дуга АВ равна 36\(\circ\), тогда угол АОВ также равен 36\(\circ\).

Вписанный угол – это угол, вершина которого лежит на окружности. Вписанный угол также должен опираться на дугу окружности.

На рисунке угол АСВ – вписанный.

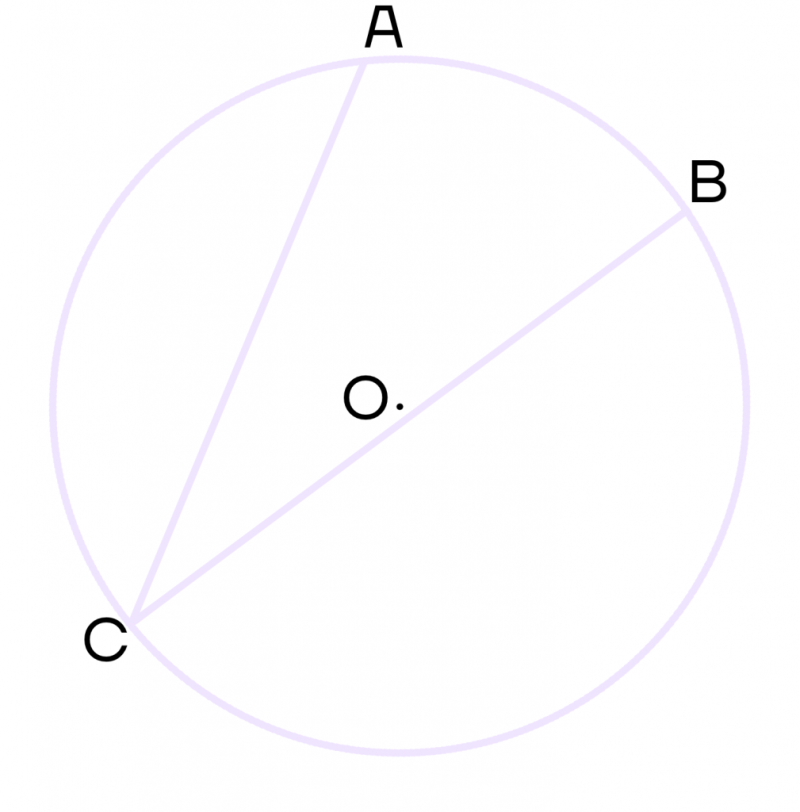
Свойства вписанного угла окружности:

Вписанный угол равен половине градусной меры дуги, на которую он опирается.

Например, дуга АВ равна 50\(\circ\), тогда угол АСВ равен 25\(\circ\).

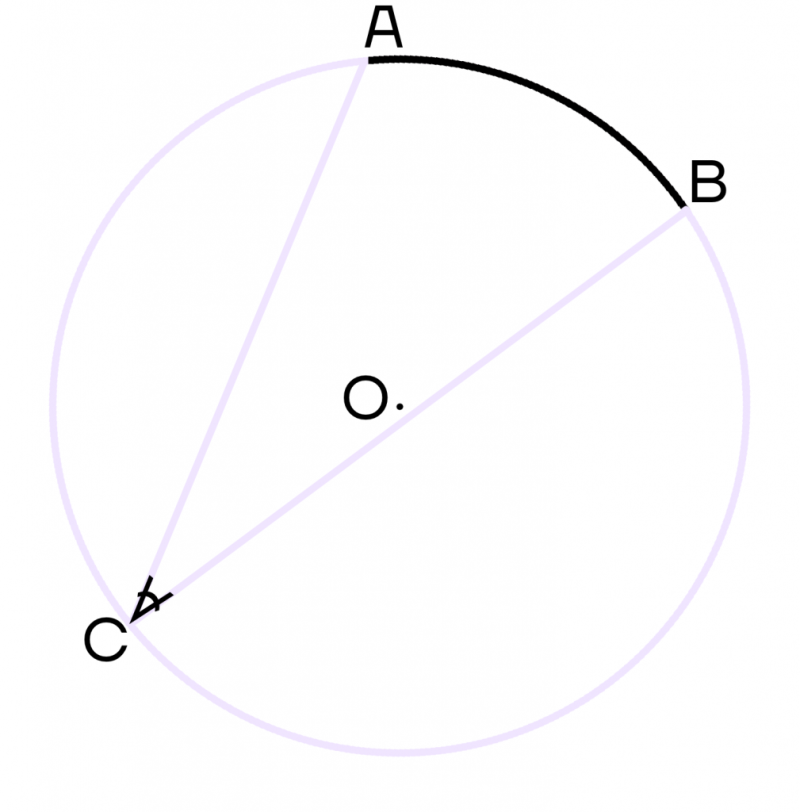
Вписанные углы, опирающиеся на одну и ту же дугу, равны.

Пусть углы АСВ, АЕВ и АКВ опираются на душу АВ. Тогда эти углы будут равны между собой.

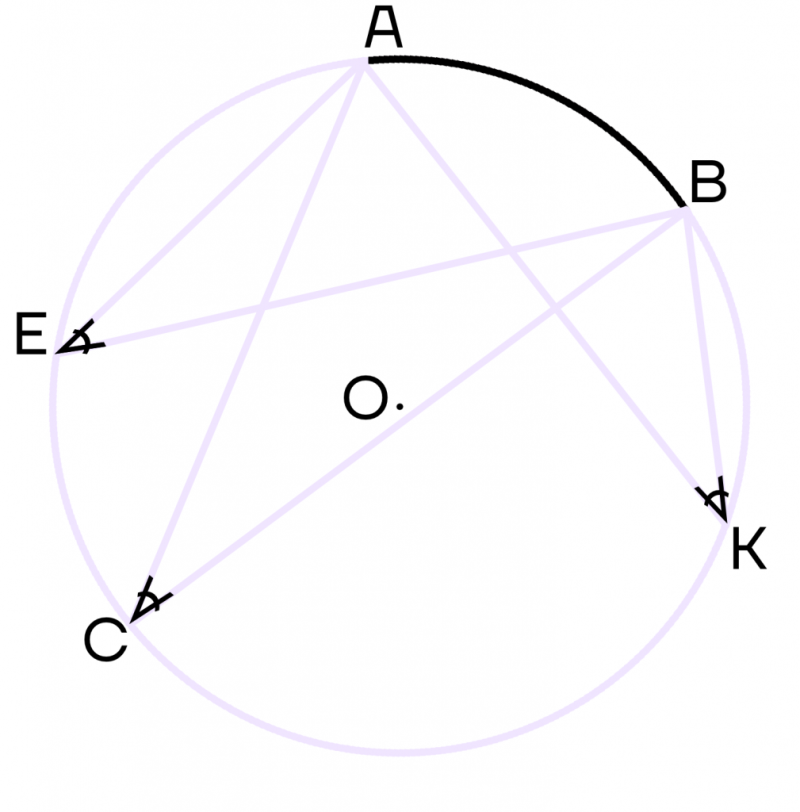
Вписанный угол, опирающийся на диаметр, равен 90\(\circ\).

Вспомним, что диаметр делит окружность на две полуокружности, градусные меры которых равны 180\(\circ\). Тогда вписанный угол будет равняться 180\(\circ\) : 2 = 90\(\circ\).

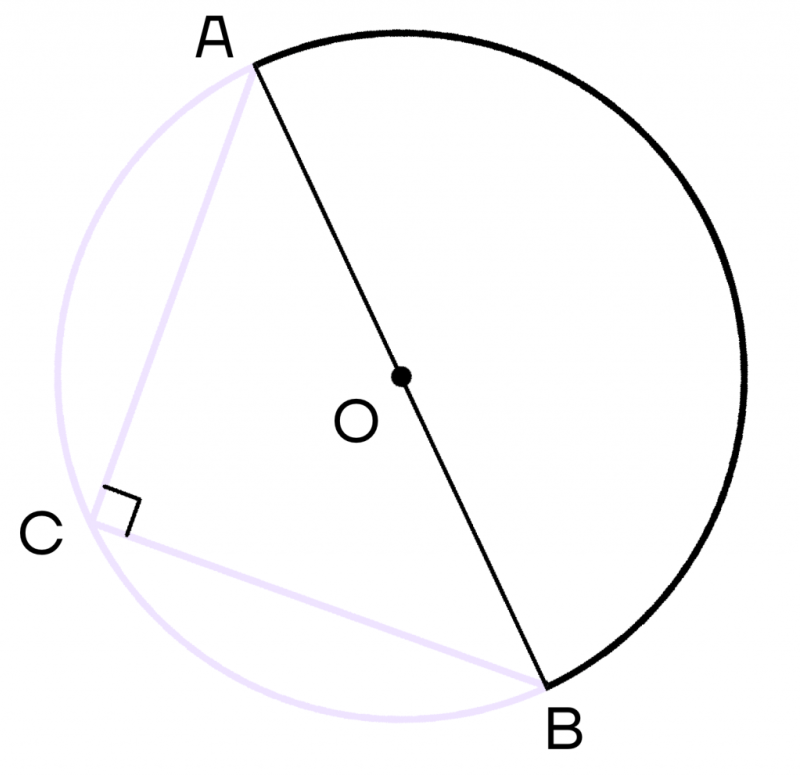
Также важно заметить, что вписанный угол равен половине центрального угла. При этом данные углы обязательно должны опираться на одну дугу.

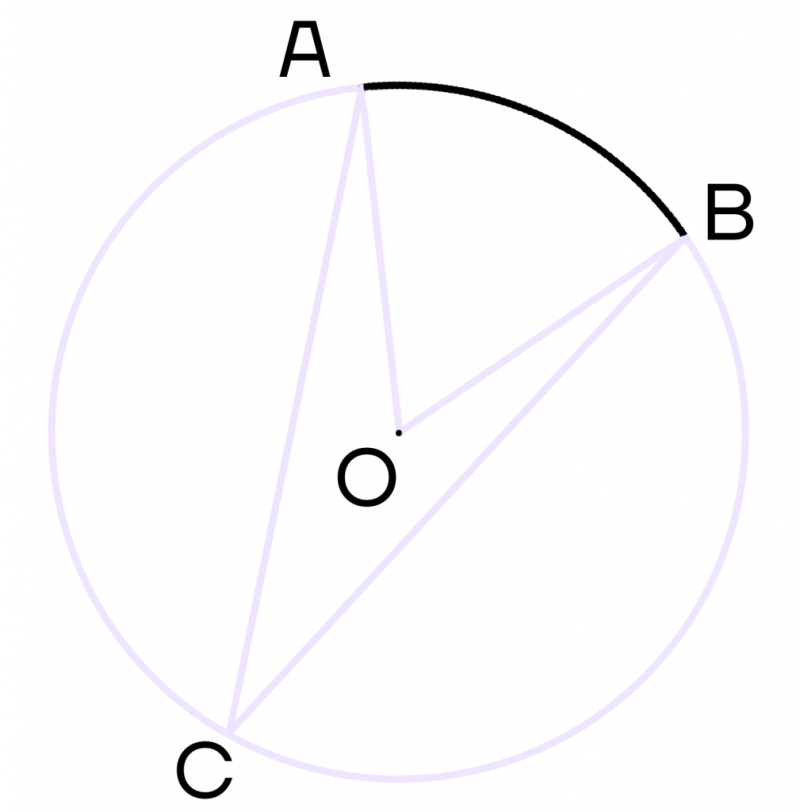
Это легко доказать, если вспомнить, что:

центральный угол равен градусной мере дуги, на которую он опирается,
вписанный угол равен половине градусной меры дуги, на которую он опирается.

Следовательно, \(∠ACB = \frac{1}{2}∠AOB\).

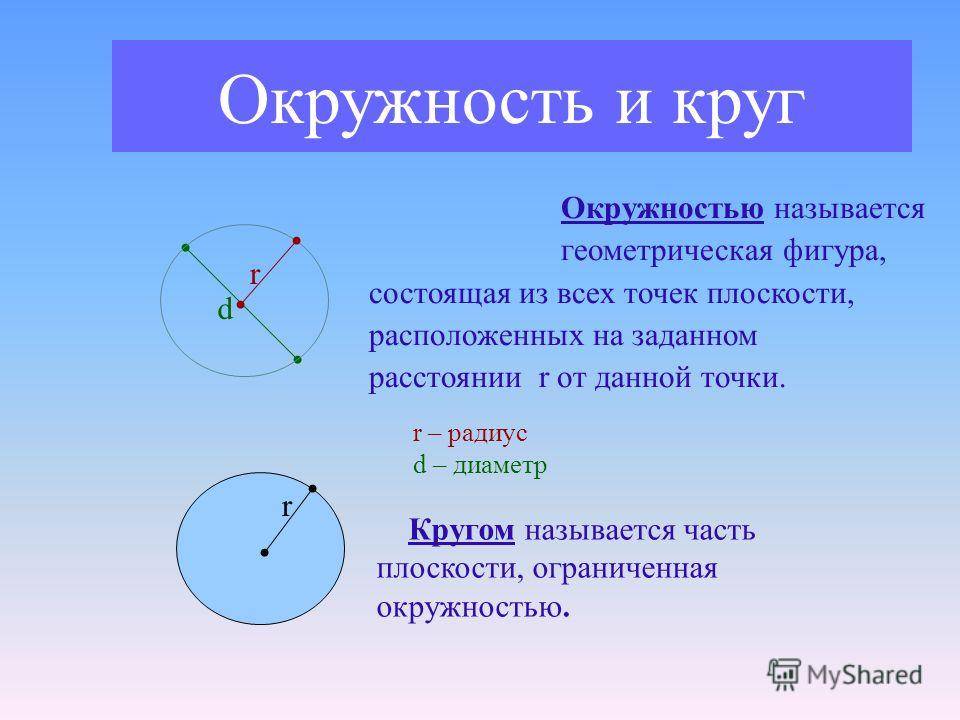
Размеры и параметры окружности

Для окружности также можно определить диаметр, который является удвоенным значением радиуса. Диаметр — это расстояние между двумя точками на окружности, проходящими через ее центр. Отношение диаметра к радиусу всегда равно 2.

Окружность также имеет периметр, который является длиной окружности. Для нахождения длины окружности используется формула: периметр = 2πr, где r — радиус окружности, а π (пи) — математическая константа, примерное значение которой равно 3,14159.

Таким образом, окружность — это геометрическая фигура, задаваемая радиусом, диаметром и периметром. Она не имеет площади и внутренних углов, так как состоит только из точек, равноудаленных от центра.

Круг в реальной жизни

В реальности можно без особых усилий отыскать множество предметов, по форме тождественных кругу. К примеру, готовый образец круга – а, точнее, множество, — каждый день катается по дорогам поселков и городов. Понятно, что речь идет о колесе. Здесь стоит оговориться: круг не должен быть однотонным, это не обязательно. Он может быть украшен узорами или чем-то еще – от этого форма не изменяется.

Колесо

Другой пример круга – Солнце. Да, то самое дневное светило, которое люди лицезреют каждый день. Любознательный читатель заметит, что Солнце – фигура объемная, она не может быть кругом. Это правда. Но маленькая фигура, какой предстает огненная звезда жителям Земли – по сути своей именно круг. Площадь его, конечно, высчитать не получится. Почему? Потому что этот пример приводится только для наглядности, для того, чтобы понять, что такое круг.

Солнце

Применение круга в математике и геометрии

Круг используется во множестве различных задач и концепций. Некоторые из его применений включают:

Вычисления площади и длины окружности: Площадь круга вычисляется по формуле S = πr², где π (пи) — это математическая константа, равная примерно 3,14159, а r — радиус круга. Длина окружности вычисляется по формуле L = 2πr. Эти вычисления могут быть полезными для решения проблем, связанных с областями, периметрами и длинами кривых.
Геометрическая оптика и астрономия: Круг используется в оптике для описания линз и зеркал, а также для вычисления пути света через линзы и преломление света. В астрономии он используется для описания орбит планет и других небесных тел.
Статистика: Круг используется в статистике для построения круговых диаграмм и отображения данных в виде секторов, пропорциональных их относительным значениям. Это позволяет наглядно представить информацию и сравнить ее части.
Механика и инженерия: Круг используется для моделирования и анализа движения колес, шестеренок и других круглых механизмов. Он также применяется в анализе сил и равновесия, формулировании уравнений движения и проектировании эффективных конструкций.
Музыка и искусство: Круг используется в музыке для измерения углов между нотами и строительства музыкальных гамм. В искусстве он может быть использован для построения и симметрии композиций, а также для создания эффектов перспективы и глубины.

Это лишь некоторые примеры применения круга в математике и геометрии, и его использование может быть намного более обширным и разнообразным

Знание основных свойств и способов работы с кругом является важной частью математической и геометрической подготовки и помогает понять и анализировать различные аспекты окружающего мира

Идеальные и реальные объекты

Важно отметить, что круг и окружность имеют разные свойства и характеристики. Например, у круга есть площадь, которая вычисляется по формуле S = πr², где r — радиус круга

У окружности же есть длина, которая вычисляется по формуле L = 2πr.

Еще одно отличие между кругом и окружностью заключается в их использовании в реальном мире. Круг часто используется в геометрии и математике для анализа и решения различных задач. Окружность же широко применяется в архитектуре, инженерии и дизайне, где она может быть использована для создания красивых, эстетически приятных форм и конструкций.

Таким образом, основные отличия между кругом и окружностью сводятся к их геометрическим характеристикам и использованию в реальном мире. Круг — это идеальная геометрическая фигура, которая имеет площадь, а окружность — это конкретная кривая, которая имеет длину и широко применяется в различных отраслях человеческой деятельности.

Видео: Что такое круг, окружность и радиус

Школьные годы для большого количества взрослых – синоним беззаботной поры детства. Вполне понятно, почему многие дети и подростки не горят желанием каждый день ходить в школу – но именно в ее стенах они получают общие знания о мире и навыки социальной жизни, которые становятся незаменимыми после получения аттестата зрелости.

Одним из таких вопросов, таких общих понятий является тема сходств и различий круга и шара. Спутать рассматриваемые понятия одновременно просто и сложно – потому что различий между кругом и шаром не так много, как кажется малоопытному ребенку.

Итак, в чем же несходства между шаром и кругом? Чем они похожи?

Что такое круг?

Начертание круга начинается с окружности. Окружность – это замкнутая черта без конца и начала, каждая точка которой находится на равном удалении от центра. Простейший пример окружности – гимнастический обруч.

Окружность

Круг

Радиус – расстояние от центральной точки круга или окружности до границы фигуры (линии, которая ее очерчивает).
Диаметр – важная характеристика, которая так часто фигурирует в школьных заданиях. Это сумма двух радиусом, то есть расстояние между двумя противоположными точками на окружности.
Площадь – свойство, характерное только для круга. Окружность не имеет его в силу своей структуры (потому что она пустая, а центр фигуры – воображаемая точка). В круге, напротив, несложно определить центр. Через центральную точку фигуры достаточно просто прочертить ряд линий, которые поделят круг на сектора.

Примеры использования круга и окружности:

1. Круг как геометрическая фигура:

Круг — это геометрическая фигура, которая состоит из точек, равноудаленных от центра. Он не имеет сторон и углов. Примером использования круга в геометрии может быть нахождение площади круга по его радиусу или диаметру. Круг также используется в конструировании колес и шестеренок.

2. Окружность как линия:

Окружность — это геометрическая фигура, которая представляет собой линию, состоящую из всех точек, равноудаленных от центра. Окружность может использоваться в геометрии для определения длины дуги, построения касательных и вычисления радиуса или диаметра. Окружность также используется в цветовой теории для построения цветовых кругов.

3. Применение круга и окружности в ежедневной жизни:

Пицца — алюминиевая форма, на которой готовится пицца, имеет форму круга, чтобы придать пицце правильную форму и равномерно распределить тепло при приготовлении.
Часы — циферблат на часах представляет собой окружность, которая используется для отображения времени. Стрелки часов также движутся по окружности для указания текущего времени.
Банковские монеты — большинство монет имеют форму круга, чтобы быть удобными для хранения, подсчета и использования в торговле.
Рули автомобилей — большинство рулей имеют форму окружности или немного заостренную форму круга, чтобы обеспечить удобное и управляемое управление автомобилем.

4. Использование круга и окружности в искусстве:

Живопись — окружность может использоваться в композиции картины для создания эффекта гармонии и баланса между элементами.
Скульптура — круг и окружность могут использоваться в форме скульптурных произведений для создания эстетической привлекательности и ощущения движения.
Дизайн — круг и окружность широко используются в дизайне для создания логотипов, упаковки, плакатов и других графических элементов.

Это лишь несколько примеров использования круга и окружности в различных областях нашей жизни. Эти геометрические фигуры имеют широкий спектр применений и играют важную роль в нашем повседневном опыте.

Выводы

Круг – плоская, двухмерная фигура. Шар – объемное трехмерное геометрическое тело. Тем не менее, они имеют массу сходств (наличие ограничивающей поверхности, диметра и радиуса, наполненность структуры в отличие от той же окружности, возможност вычислить площадь).

Чем же отличается круг от шара? Круг плоский, шар же имеет объем. Именно объемность шара позволяет ему делиться на сечения, которые по своей сути являются кругами. Круг, напротив, делится на сектора.

Публикации по теме:

Детско-родительский игровой сеанс «Круг» для детей ОВЗ Игровое занятие КРУГ для детей ОВЗ Тема «Осень. Природные явления» Цели и задачи занятия КРУГ Главная цель занятия КРУГ – дать каждому ребенку.

Конкурс профессионального мастерства «Солнечный круг» (фотоотчет) С 12 по 26 октября 2015 года в нашем детском саду проходил конкурс профессионального мастерства «Воспитатель года». Цель конкурса: выявление.

Конспект НОД по ФЭМП «Знакомьтесь: круг» Конспект НОД по ФЭМП во второй младшей группе «Знакомьтесь- круг» Цель: развитие познавательных интересов детей Задачи: Познакомить.

НОД по математике «Круг и квадрат» (младшая группа) Тема: «Круг и квадрат» (младшая группа) Образовательная область: познание Цель: Продолжать учить находить один и много предметов в специально.

Поделки в технике «объемный квиллинг» Здравствуйте, коллеги! Недавно открыла для себя технику объемного квиллинга. Искусство, которое на русском языке называют «бумагокручением»,.

Проект по математическому развитию «Круг, квадрат и треугольник-фигуры важные, фигуры нужные» Номинация проекта – «Дошкольный возраст» Вид проекта: долгосрочный, фронтальный. Участники проекта: подгруппа детей средней группы, воспитатель.

«Снежинка 3-D». Объемный модуль для украшения интерьера Приближаются Новогодние праздники и перед нами, как воспитателями опять стоит вопрос «Чем же удивить детей и взрослых?». Просторы Интернета.

Совместная образовательная деятельность по ФЭМП «Круг и квадрат» Совместная образовательная деятельность взрослого и детей ФЭМП «Круг и квадрат». Цель: закреплять умение различать и называть круг и квадрат.

Весенний объемный тюльпан на открытке в подарок маме Не за горами прекрасный весенний праздник 8 Марта. И уже сейчас многие педагоги задумались над тем, что бы смастерить с детьми мамам в.

Разбираемся в том что такое окружность и круг. Формула площади круга и длины окружности.

Мы каждый день встречаем множество предметов, по форме которые образовывают круг или напротив окружность. Иногда возникает вопрос, что такое окружность и чем она отличается от круга. Конечно же, мы все проходили уроки геометрии, но иногда не помешает освежить знания весьма простыми объяснениями.

Выводы

Публикации по теме:

На уроках геометрии в школе все мы изучали свойства различных фигур и линий. Каждая из них имеет свои особенности, а порой некоторые из них взаимосвязаны друг с другом. Взять для примера хотя бы круг и окружность – между ними есть определенная связующая линия. Только вот какая? Давайте вместе разберемся в этом вопросе.Окружность
представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности. Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность. Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится. По этой причине имеется четкое понятие, что окружность делит всю плоскость на две части – внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, поскольку плоскость в общем понимании не имеет границ.Круг
является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность. Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.
Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии. Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга. Иными словами, круг представляет собой не только окружность, которая является его границей, но также и то бесконечное число точек, находящихся внутри этой окружности.