Чем отличается окружность от круга

Единицы времени

Каждый человек хочет понять время. Оно нам нужно, потому что мы живем по режиму, а магазины, библиотеки, вокзалы — по расписанию. Определенное количество дел намечаем сделать в единицу времени.

Давайте познакомимся с единицами измерения времени.

Земля обращается вокруг Солнца за 365 суток. Это год. Один раз в 4 года он увеличивается на сутки, и называется високосным.

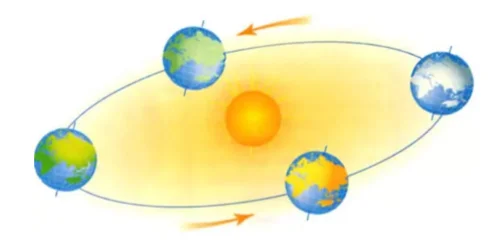
С глубокой древности круг считается символом годовых сезонных циклов: зимы, весны, лета и осени. Рассмотрите рисунок годового круга: он поделен на 4 доли — четыре времени года.

Единица величины каждого времени года делится на 3 месяца.

В году 3 ∙ 4 = 12 месяцев. Месяц — единица времени, за которую Луна обходит планету Земля вокруг.

В каждом месяце 30 или 31, а в феврале 28 или 29 суток.

Исторически основной единицей для времени были сутки (часто говорят «день»). За одни сутки Земля поворачивается вокруг своей оси.

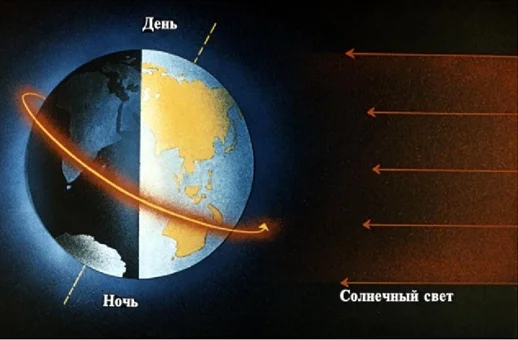
В результате деления суток на меньшие временные интервалы возникли часы, минуты и секунды. Сутки – единица времени, равная 24 часам. Один час — это 60 минут. Минута состоит из 60 секунд.

Выполните задания

1. Выразите время в указанных единицах измерения

8 ч 25 мин. = … мин.	95 мин. = … ч … мин.
2 мин. 14 сек. = … сек.	187 сек. = … мин. … сек.

Решение:

1 час = 60 мин. Значит, в восьми часах будет в 8 раз больше. Нужно выполнить умножение.

60 ∙ 8 = 480 (мин.)

В 8 часах — 480 минут да еще 25 мин. Действие сложения.

480 + 25 = 505 (мин.)

Ответ: 8 ч 25 мин. = 505 мин.

Дальше решайте аналогично:

2 мин. 14 сек. = 60 ∙ 2 + 14 = 134 сек.

95 мин. = 1 ч 35 мин.

187 сек. = 3 ч. 7 сек.

2. Выберите единицы времени, которые расположены в порядке возрастания

а) час, минута, секунда

б) секунда, минута, час

в) минута, час, секунда

Проверьте себя.

Правильный ответ — б.

3. Автомобиль до Москвы едет 2 суток, а обратно 48 часов. Почему такая разница?

Проверьте себя.

2 сут. = 48 ч. Разницы нет.

Наш урок подходит к концу. Я надеюсь, что вы будете ценить свое время, не будете терять его зря.

Я с вами прощаюсь, а вы проверьте свои знания.

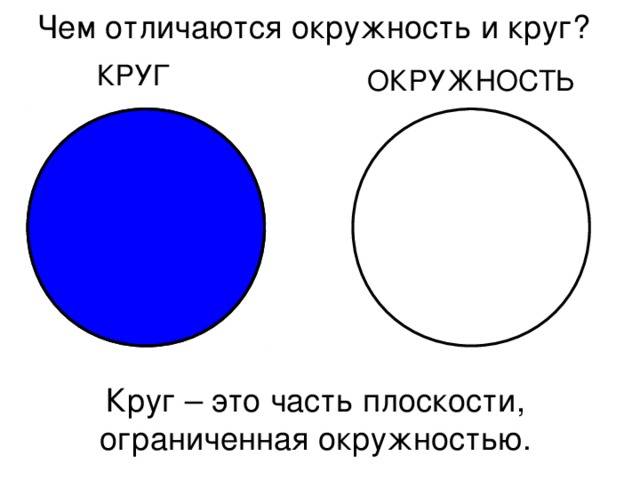
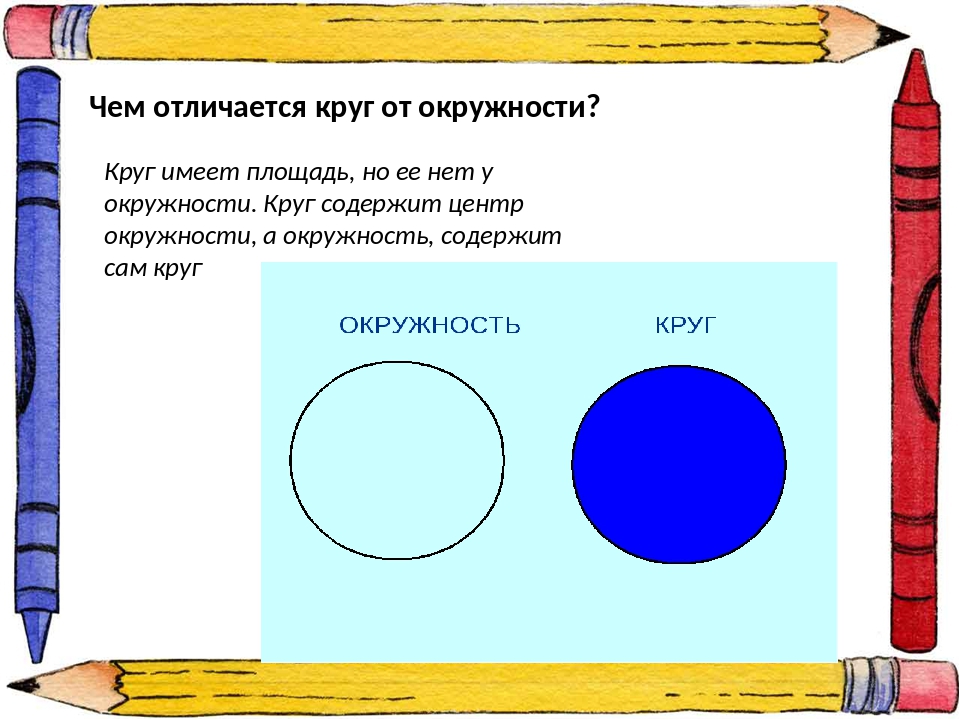
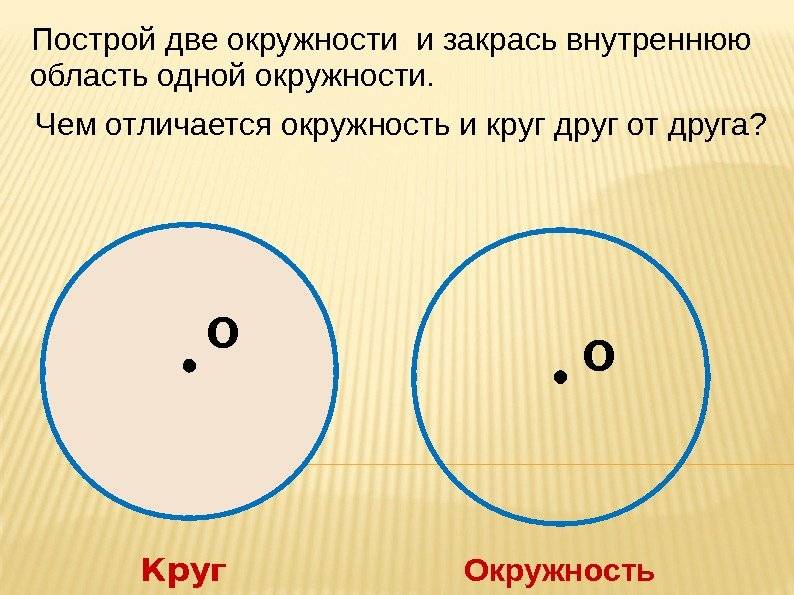
Отличия между окружностью и кругом:

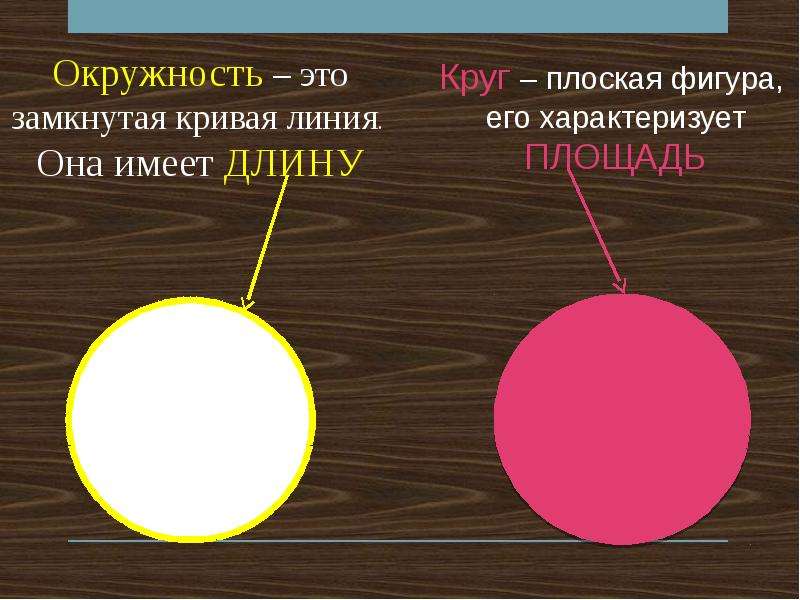
Геометрические формы: окружность — это замкнутая кривая, состоящая из всех точек, находящихся на одинаковом расстоянии от определенной точки, называемой центром; круг — это плоская фигура, ограниченная окружностью и состоящая из всех точек, находящихся на одинаковом расстоянии от центра.
Размер: окружность не имеет площади и описывается только длиной окружности, которая вычисляется по формуле 2πr (где r — радиус окружности); круг имеет площадь, вычисляемую по формуле πr^2 (где r — радиус круга).
Применение: окружности используются в геометрии и математике для решения задач, определения расстояний и построения графиков; круги используются не только в геометрии, но и в различных областях, таких как инженерия, физика, архитектура, искусство и дизайн.
Свойства: окружность имеет радиус, диаметр, дугу и центр; круг имеет радиус, диаметр, центр и площадь.
Отношение к другим фигурам: окружность является частным случаем эллипса, а круг является частным случаем окружности.

Важно знать различия между окружностью и кругом, чтобы правильно использовать эти термины и понимать их характеристики при решении геометрических задач и анализе фигур

Понятие доли

Вы когда-нибудь заглядывали в тетради к старшеклассникам? Смотрите, какой у меня пример.

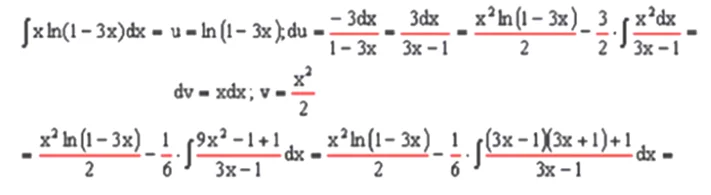
Видите сложение, вычитание, умножение? Знаки этих действий известны: плюс, минус, точка. Деление же в примере обозначено горизонтальной чертой.На рисунке она выделена красным цветом. Я расскажу, когда в математике используют черту.

Мы умеем делить несколько предметов, но часто деление нужно, чтобы раздробить одно число на равные части — доли от целой величины.

Один разделить на два — это одна вторая. Что же это такое?

В жизни вы часто так делали. Например, один апельсин делили с другом: брали нож и разрезали его пополам.

Каждый из вас получал половину или одну долю.

На лесной полянке собралось девять друзей, апельсин делили на всех. Рассмотрите рисунок. Как называется каждая часть фрукта?

Совершенно верно, это долька. Апельсин поделили на 9 одинаковых долек.Каждая 1 долька апельсина — это одна из девяти равных долей целого фрукта.

Вы теперь поняли, ребята, что в жизни человеку приходится не только пересчитывать предметы, но и делить (дробить) целое на части, вот так появилось в математике понятие доли и дроби.

Знак доли (дроби) обозначают дробной горизонтальной или наклонной чертой. Например, так — 1/9 (одна девятая). Запись придумали арабы в 16 веке.

Доли называют по количеству частей раздробленного одного предмета:

Разделите, например, яблоко на две равные части, у вас получится название доли «половина» или 1/2 (одна вторая)
Разрежьте яблоко на три части. Один кусок — это «треть» — 1/3 (одна третья)
Разломите на четыре доли — «четверть» — 1/4 (одна четвертая)

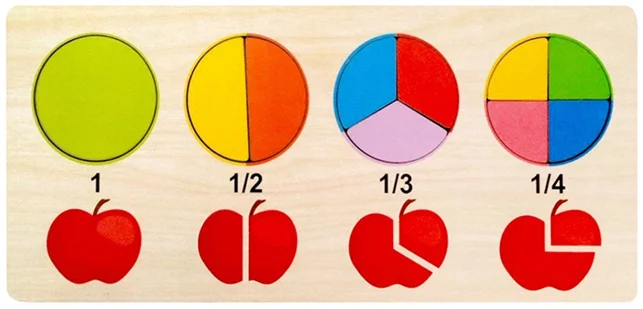
Знание о долях помогает решить задачи.

Запомните правило по математике нахождения доли.Чтобы найти долю от числа надо число разделить на эту долю. В дроби число, на которое делят, записано под чертой и называется знаменателем. То число, которое надо разделить, пишут над чертой. Это числитель.

Задание 1

Найдите пятую долю от числа 25. Это значит, что надо выполнить действие деления.

Привычный пример 25 : 5 можно записать вот таким образом:

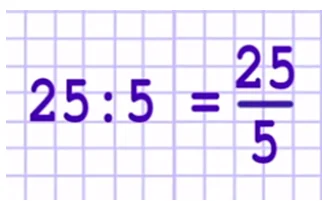
Или так — 25/5. 25 – это числитель, а 5 — знаменатель.

25: 5 = 5

Ответ: одна пятая доля от числа 25 равна пяти.

Задание 2

Чему равна 1/4 доля от полоски длинной 16 см?

Полоску согните пополам, ещё раз пополам. Разверните. На сколько долей линией сгиба разделили полоску? Правильно, на 4.

Закрасьте одну такую долю.

Какую долю вы закрасили? (одну четвёртую)

16 : 4 = 4(см)

Ответ: длина одной четвертой доли полоски составляет 4 см.

Задание 3

Решите задачи на понятие доли. Рассмотрите рисунки. Какая доля каждой фигуры закрашена серым цветом?

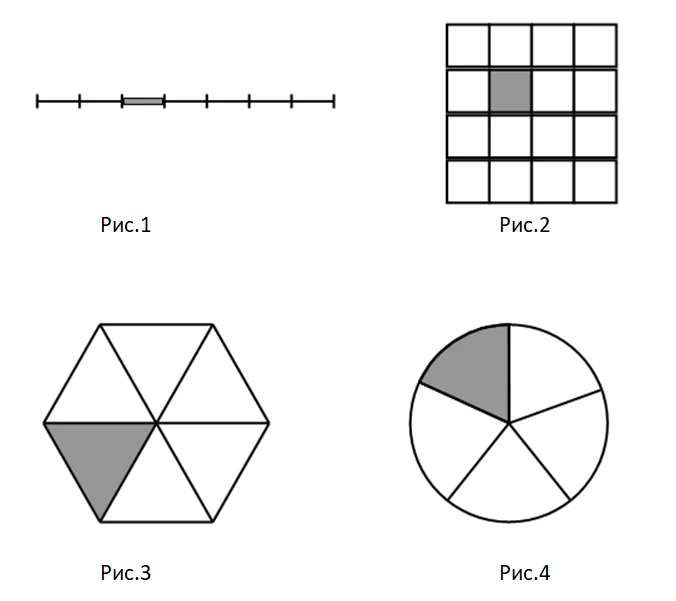
Рассуждаем так.

На рисунке 1 отрезок разделили на 7 частей.Значит, закрашена одна седьмая (1/7) доля фигуры.

Проверьте:

На следующих рисунках заштрихована 1/16 доля квадрата, 1/6 доля шестиугольника, 1/5 доля круга.

Чтобы разобрать понятие массовой доли, представьте себе килограмм яблок (1000 г), который мама купила своим трем детям.

Из этого килограмма самому младшему ребенку досталась половина всех яблок (несправедливо, конечно!). Старшему — лишь 200 г, а среднему — 300 г.

Значит, массовая доля яблок у младшего ребенка составит половину, или одну вторую (1/2) массовую долю.

У старшего ребенка будет:

1000 : 200 = 5 — одна пятая (1/5) массовая доля

Далее рассуждаем так:

Младшему ребенку дали половину яблок.

1000 : 2 = 500(г)

Яблоки разделили между детьми по 500г, 200г и 300г. Вы знаете, что 500 — это 5 сотен, 200 — 2 сотни, 300 — 3 сотни.

На сколько сотен разделили все яблоки?

5 сотен + 2 сотни + 3 сотни = 10 сотен.

Сколько граммов будет в одной десятой доле?

1000 : 10 = 100 (г) в одной десятой доле

У среднего ребенка 300 г. Во сколько раз больше, чем 100 г?

300 : 100 = 3

В три раза. Значит, у среднего ребенка будет не одна, а три десятых массовых долей 3/10.

Ребята, вы молодцы. Верное решение.

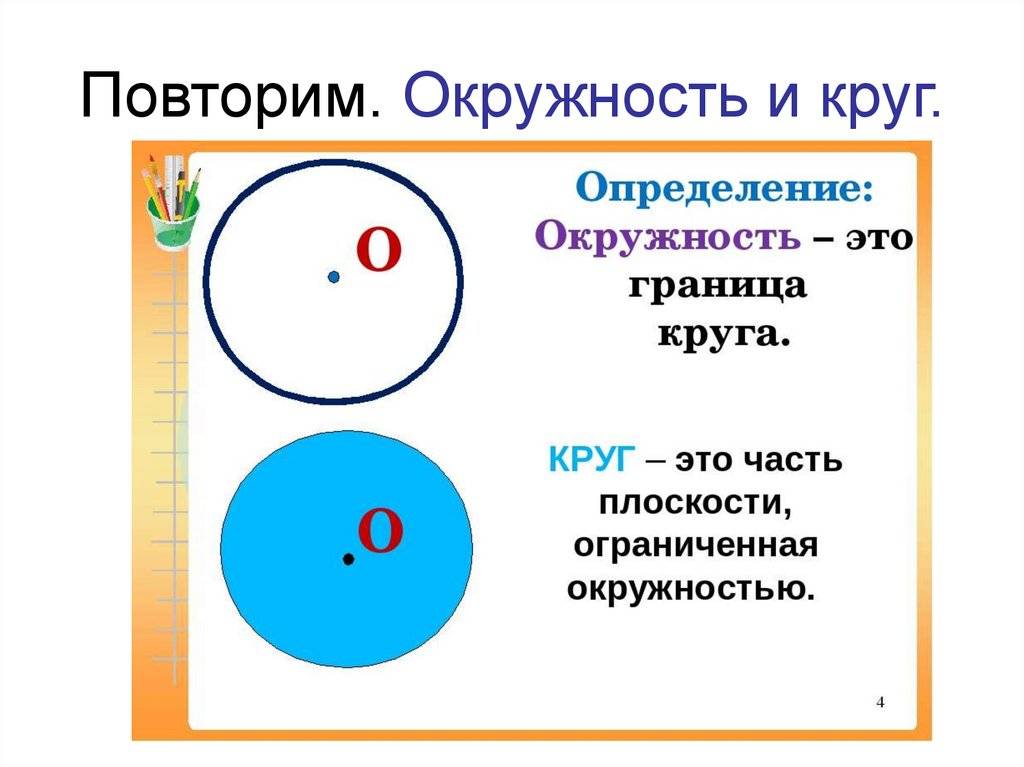
Окружность и круг: основные различия

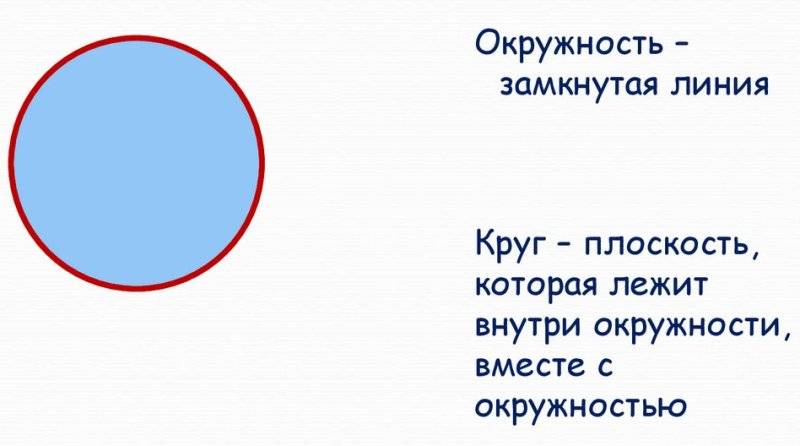
В геометрии окружность и круг смыслово связаны, но имеют некоторые отличия. Окружность — это геометрическая фигура, представляющая собой линию, состоящую из всех точек, равноудаленных от центра. Круг же — это теоретическая плоская фигура, ограниченная окружностью.

Главным отличием между окружностью и кругом является то, что окружность не имеет площади, в то время как круг — это круглая фигура с определенной площадью. Круг может быть задан с помощью радиуса и центра, который является точкой внутри круга.

Другое различие между окружностью и кругом заключается в их диаметрах. Диаметр — это отрезок, соединяющий две точки на окружности и проходящий через центр круга. В окружности диаметром считается любой отрезок, проходящий через центр, в то время как в круге диаметр — это двойной радиус.

Таким образом, главная разница между окружностью и кругом заключается в том, что окружность является линией, состоящей из точек, равноудаленных от центра, в то время как круг — это ограниченная этой окружностью плоская фигура с определенной площадью. Кроме того, окружность не имеет площади, в отличие от круга.

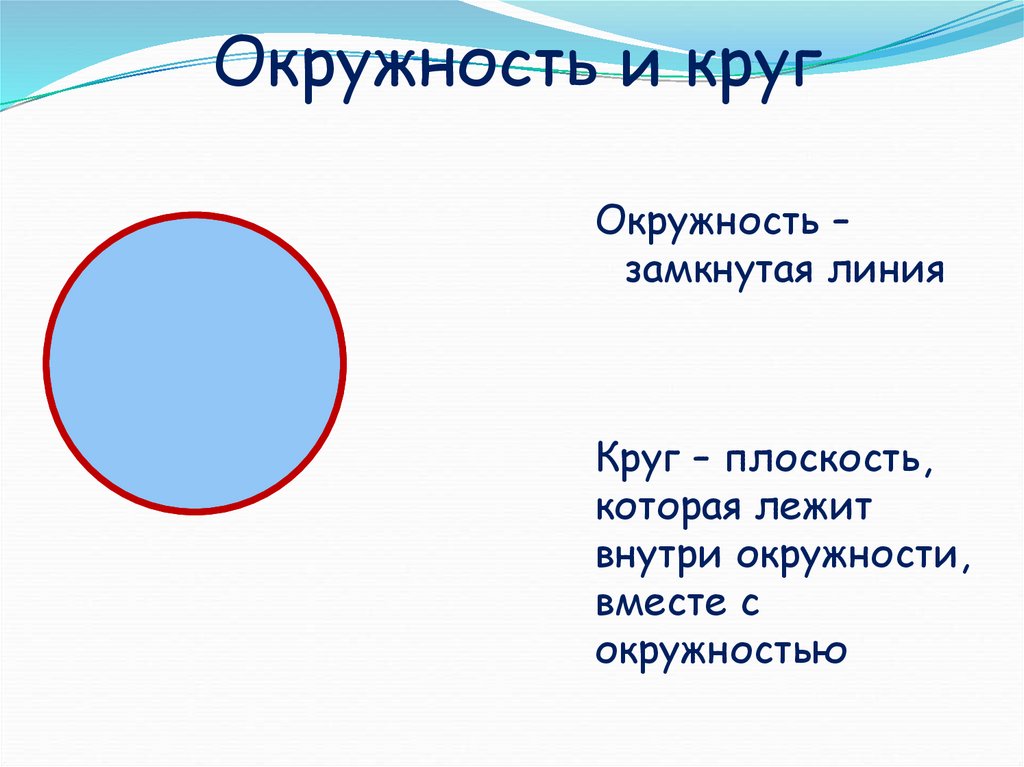
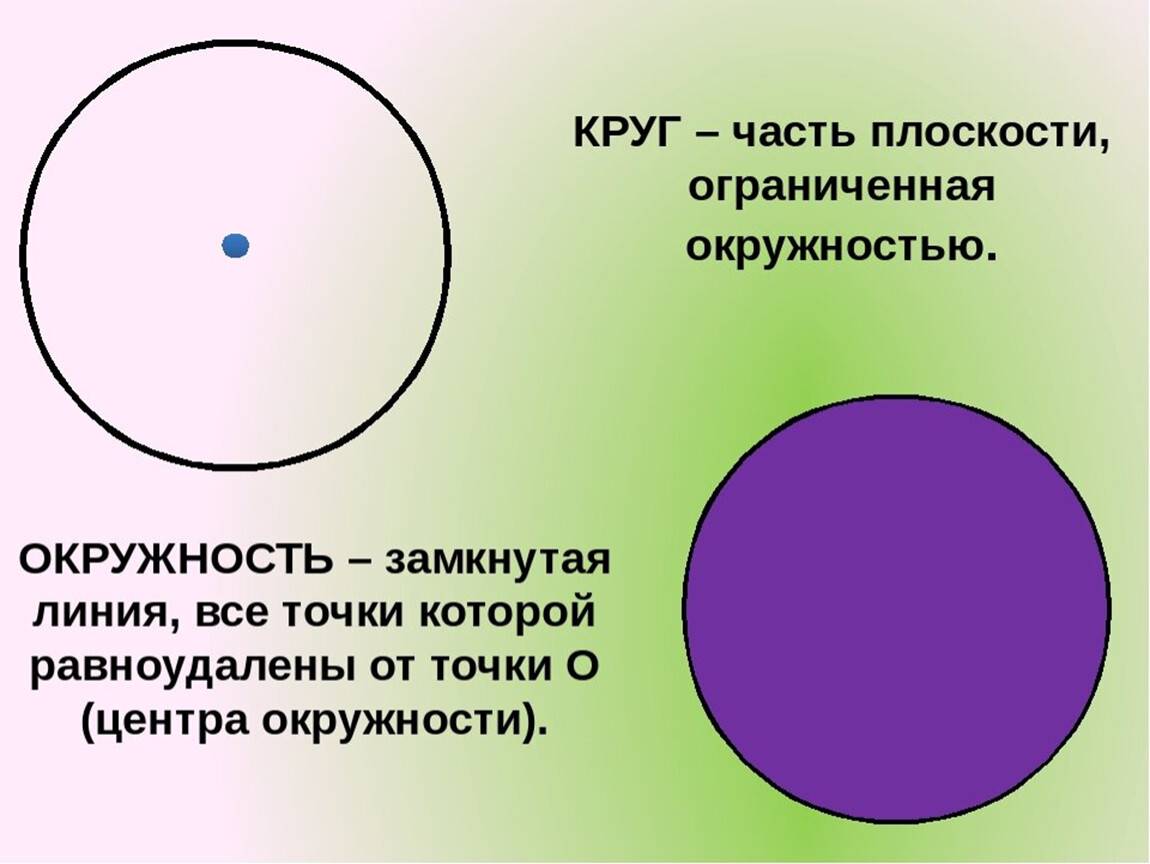
Определение и форма

Окружность и круг — две понятия из области геометрии, которые отличаются друг от друга. Окружность — это геометрическая фигура, состоящая из множества точек, которые находятся на одинаковом расстоянии от центра. Центр окружности — это точка, от которой все точки окружности расположены на одинаковом расстоянии, называемом радиусом.

Теория окружностей в геометрии изучает их свойства и особенности. Окружность является формой, которая не имеет начала и конца, она представляет собой замкнутую линию, состоящую из бесконечного числа точек.

Круг — это закрашенная фигура, которая образуется при закрашивании внутренней части окружности. Круг представляет собой плоскую геометрическую фигуру, ограниченную окружностью. Диаметр круга — это отрезок, соединяющий две точки на окружности круга и проходящий через его центр. Диаметр является максимальной длиной от точки к точке на окружности.

В качестве иллюстрации можно представить таблицу с описанием различий между окружностью и кругом:

Окружность	Круг
Геометрическая фигура	Закрашенная фигура
Бесконечная линия	Ограниченная плоская фигура
Состоит из множества точек на одинаковом расстоянии от центра	Состоит из закрашенной области внутри окружности
Центр и радиус определяют окружность	Центр и радиус определяют круг, а также диаметр

Что такое окружность?

Окружность – это геометрическая фигура, которая представляет собой замкнутую линию на плоскости. Она состоит из всех точек, расположенных на одинаковом расстоянии от определенной точки, которую называют центром окружности.

Один из основных параметров окружности – это радиус, который определяет расстояние от центра до любой точки на окружности. Также можно выразить радиус через диаметр окружности. Диаметр – это отрезок, проходящий через центр окружности и соединяющий две противоположные точки на окружности.

Окружность можно охарактеризовать свойствами ее периметра и площади. Периметр окружности вычисляется по формуле 2πr, где r – радиус окружности. Площадь окружности вычисляется по формуле πr².

Чтобы иллюстрировать свойства окружности и ее параметры, можно использовать таблицу или графические примеры. Например, в таблице можно привести значения радиуса, диаметра, периметра и площади окружности для различных значений.

Что такое круг?

Круг — это геометрическая фигура, которая образуется на плоскости при вращении точки вокруг определенной оси, которая называется центром. Линия, которую описывает точка при вращении, называется окружностью. Окружность состоит из всех точек, которые находятся на одинаковом расстоянии от центра.

Одной из основных характеристик круга является его радиус. Радиус — это расстояние от центра круга до любой его точки. Другая основная характеристика круга — диаметр. Диаметр — это отрезок, который соединяет две противоположные точки на окружности и проходит через центр.

Также важным понятием в теории круга является площадь. Площадь круга вычисляется по формуле S = π * r^2, где π — приближенное значение математической константы, равное примерно 3.14, а r — радиус круга.

Круг можно представить с помощью таблицы, где будут указаны его основные характеристики: радиус, диаметр, площадь. Используя эту таблицу, можно легко вычислить значение радиуса или площади круга, если известны другие характеристики.

Отличия окружности от круга

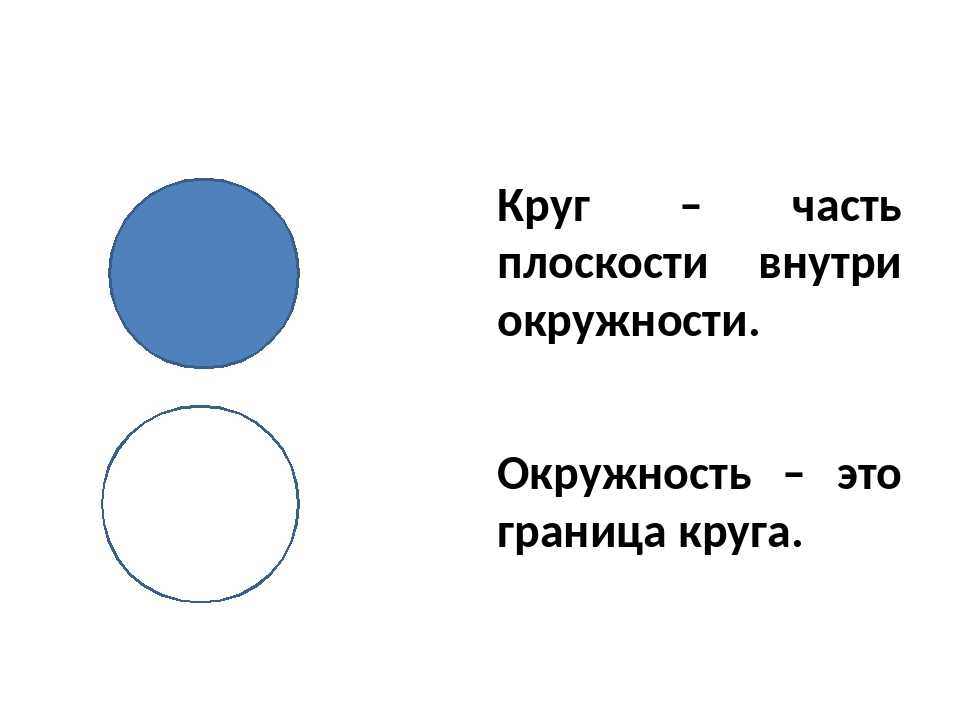
Значит, какой вывод мы можем сделать? Чем отличается окружность от круга, так это тем, что у последнего есть площадь, и в большинстве случаев окружность является границей круга. Хотя бывают и исключения на первый взгляд. Может показаться иногда, что нет окружности в круге, но это не так. В любом случае что-то да есть. Просто окружность может быть очень маленькой, и тогда ее не видно невооруженным глазом.

Также окружностью может быть то, что выделяет круг из фона. Например, на приведеном выше изображении синий круг находится на белом фоне. А вот та черта, по которой мы понимаем, что здесь начинается фигура, и называется в данном случае окружностью. Таким образом, окружность – это граница круга. Вот чем отличается окружность от круга.

Основные определения и свойства

Фигура	Рисунок	Определения и свойства
Окружность		Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Дуга		Часть окружности, расположенная между двумя точками окружности
Круг		Конечная часть плоскости, ограниченная окружностью
Сектор		Часть круга, ограниченная двумя радиусами
Сегмент		Часть круга, ограниченная хордой
Правильный многоугольник		Выпуклый многоугольник, у которого все стороны равны и все углы равны
	Около любого правильного многоугольника можно описать окружность

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Дуга

Часть окружности, расположенная между двумя точками окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Сектор

Часть круга, ограниченная двумя радиусами

Сегмент

Часть круга, ограниченная хордой

Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность

Определение 1. Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2. Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.

Замечание 1. Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.

Определение 3. Числом π (пи) называют число, равное площади круга радиуса 1.

Замечание 2. Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.

Секущая окружности и дуга окружности

Всякая секущая (прямая линия) пересекает окружность в двух точках и делит ее на две дуги. Величина дуги окружности зависит от расстояния между центром и секущей и измеряется по замкнутой кривой от первой точки пересечения секущей с окружностью до второй.

Дуги
окружности делятся секущей
на большую и малую, если секущая не совпадает с диаметром, и на две равные дуги, если секущая проходит по диаметру окружности.

Если секущая проходит через центр окружности, то ее отрезок, расположенный между точками пересечения с окружностью, есть диаметр окружности, или самая большая хорда окружности.

Чем дальше секущая расположена от центра окружности, тем меньше градусная мера меньшей дуги окружности и больше – большей дуги окружности, а отрезок секущей, называемый хордой
, уменьшается по мере удаления секущей от центра окружности.

Определение. Кругом называется часть плоскости, лежащая внутри окружности.

Центр, радиус, диаметр окружности являются одновременно центром, радиусом и диаметром соответствующего круга.

Так как круг – это часть плоскости, то одним из его параметров является площадь.

Правило. Площадь круга (S
) равна произведению квадрата радиуса (r 2
) на число ¶.

Примеры
Дано: r = 100 см
Площадь круга:
S = 3,14 * 100 см * 100 см = 31 400 см 2 ≈ 3м 2
Дано: d = 50 мм
Площадь круга:
S = ¼ * 3,14 * 50 мм * 50 мм = 1 963 мм 2 ≈ 20 см 2

Если в круге провести два радиуса к разным точкам окружности, то образуется две части круга, которые называется секторами
. Если в круге провести хорду, то часть плоскости между дугой и хордой называется сегментом окружности
.

Геометрические отличия

Окружность — это плоская фигура, представляющая собой замкнутую кривую линию, в которой все точки равноудалены от центра. Форма окружности является одним из базовых понятий геометрии и используется во множестве математических и физических задач. Окружность имеет одну основную характеристику — радиус, который определяет расстояние от центра окружности до любой ее точки.

Круг, с другой стороны, не только имеет форму окружности, но и занимает плоскость, ограниченную этой окружностью. Другими словами, круг — это все точки плоскости, которые находятся на расстоянии не больше заданного радиуса от центра. Круг также имеет свой периметр, который представляет собой длину окружности, а также свою площадь, которая вычисляется по формуле S = πR^2, где R — радиус.

Таким образом, геометрическим отличием между окружностью и кругом является то, что окружность — это одномерный объект, представляющий собой замкнутую кривую линию, а круг — двумерный объект, занимающий плоскость. Круг имеет как периметр, так и площадь, в то время как окружность имеет только радиус, который определяет расстояние от центра до точек на окружности.

Окружность	Круг
Одномерный объект	Двумерный объект
Имеет только радиус	Имеет радиус, периметр и площадь

Разные фигуры

Окружность — это геометрическая фигура, которая состоит из всех точек на плоскости, находящихся на одинаковом расстоянии от определенной точки, называемой центром окружности. Радиус — это расстояние от центра окружности до любой точки на окружности.

Круг — это особый вид окружности, который представляет собой плоскую фигуру, заключенную внутри окружности. Круг можно описать как множество всех точек на плоскости, находящихся на одинаковом расстоянии от центра окружности. Диаметр — это линия, проходящая через центр круга и состоящая из двух равных отрезков, соединяющих две точки на окружности.

Периметр — это сумма всех сторон или отрезков, ограничивающих геометрическую фигуру. Для окружности периметр вычислять не нужно, так как он равен бесконечности. В то же время, для круга периметр можно вычислить, используя формулу 2πr, где r — радиус круга.

Размеры и параметры

Определение размеров и параметров круга позволяет нам вычислить его периметр, то есть длину его окружности. Длина окружности прямо пропорциональна диаметру и может быть вычислена по формуле:

периметр = диаметр * пи (π).

Где «пи» (π) — математическая константа, которая применяется для вычисления длины окружности, и имеет значение примерно равное 3.14159. Таким образом, периметр круга можно вычислить, зная его диаметр или радиус.

Круг, как фигура в плоскости, имеет гладкую форму и не имеет углов. Его элементами являются только радиус, диаметр и окружность. Благодаря этим параметрам круг находит широкое применение в различных сферах науки, техники и повседневной жизни.

Что такое окружность: основные постулаты

не иметь общих точек;
иметь одну общую точку, при этом прямая называется касательной: если провести радиус через центр и точку касания, то он будет перпендикулярен касательной;
иметь две общие точки, при этом прямая называется секущей.

2. Через три произвольные точки, лежащие в одной плоскости, можно провести не более одной окружности.

3. Две окружности могут соприкасаться только в одной точке, которая расположена на отрезке, соединяющем центры этих окружностей.

4. При любых поворотах относительно центра окружность переходит сама в себя.

5. Что такое окружность с точки зрения симметрии?

одинаковая кривизна линии в любой из точек;
относительно точки О;
зеркальная симметрия относительно диаметра.

6. Если построить два произвольных вписанных угла, опирающихся на одну и ту же дугу окружности, они будут равны. Угол, опирающийся на дугу, равную половине то есть отсеченную хордой-диаметром, всегда равен 90°.

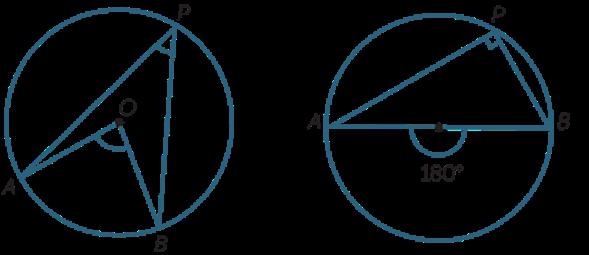
7. Если сравнивать замкнутые кривые линии одинаковой длины, то получится, что окружность отграничивает участок плоскости наибольшей площади.

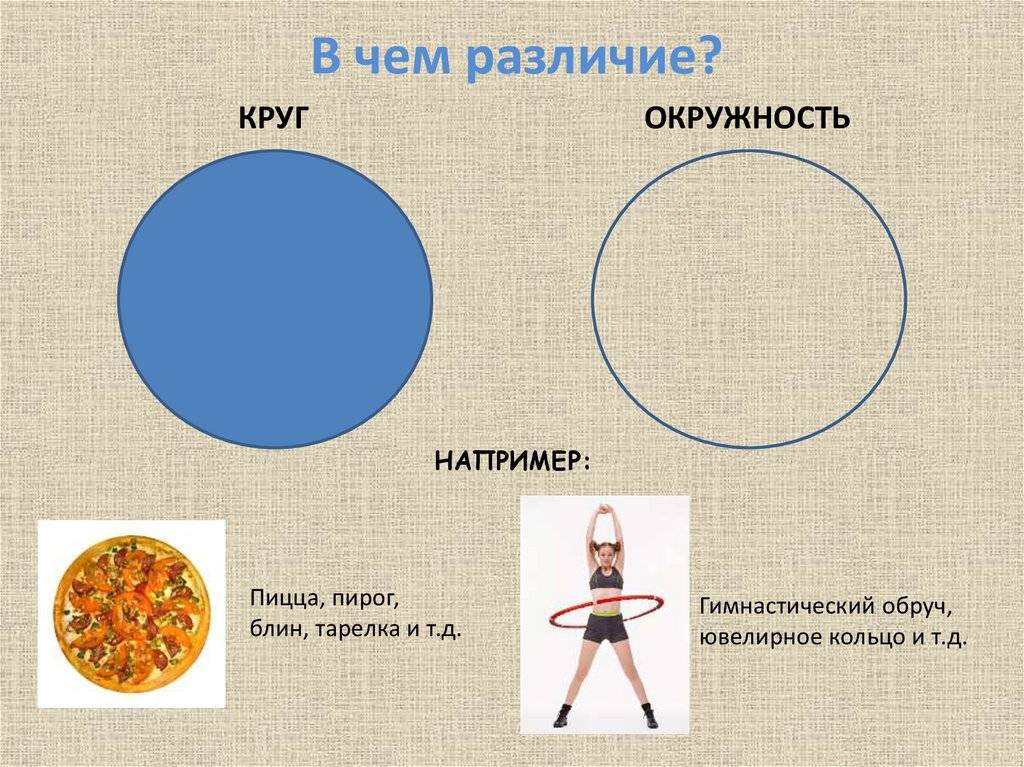
ImGist определил, что разница между кругом и окружностью заключается в следующем:

Окружность является лишь частью круга, его границей, в то время как круг является более обширной и полноценной фигурой;
Окружность – это кривая линия, состоящая из бесчисленного множества точек, равноудаленных от центра, а круг представляет собой не только сумму этих точек окружности, но также и все те точки, которые расположены внутри этой самой окружности.

Окружность
– это огромное количество точек на плоскости, равноудаленных от некой точки этой же плоскости, именуемой центром окружности. Окружность представляет собой замкнутую кривую, лежащую от центра на фиксированном расстоянии, нарываемом радиусом окружности.

Круг
– это огромное количество точек плоскости, удаленных от некой точки этой же плоскости, именуемой центром круга, на расстояние, не превышающеей определенной величины, именуемой радиусом круга. Круг представляет собой сплошную фигуру, включающую окружность и все точки, лежащие в ней.

Следовательно, круг – это участок плоскости, а окружность – черта этого участка. Потому есть возможность говорить о площади круга и длине окружности, однако неправильно говорить о длине круга и площади окружности.

Так как точки окружности удалены от центра на расстояние, не превышающее радиуса, то они все принадлежат кругу. Другими словами, окружность принадлежит кругу, который она ограничивает. В особых случаях может рассматриваться круг в отсутствие границы – огромное количество точек круга, не принадлежащих его границе (окружности).

Окружность разделяет плоскость на две части – лежащую снутри и лежащую снаружи. Попрасть из одной части в другую нереально в отсутствие скрещения окружности. Площаль внутренней части конечна, площадь наружной части нескончаема.

Центр окружности не принадлежит окружности (кроме вырожденного варианта окружности нулевого радиуса). Центр круга всегда принадлежит кругу, т.к. находится снутри ограничивающей его окружности.

openclass.ru – методическая разработка «Окружность и круг»
otvet.mail.ru – чем отличается круг от окружности?

NMitra
В Opera есть баг: у вложенного элемента углы не закругляются. Это можно подправить, дописав

#ball:after {content: “”;position: absolute;top: 0; bottom: 0; right: 0; left: 0;box-shadow: 0 0 0 100px #fff;border-radius: 100%; }

Но тогда тень в Гугл Хром “обрезанная” получается. Поскольку Опера переезжает на движок Google, то я сделала выбор в пользу его браузера.
Космо Мизраил
Прикольно.Сейчас делаю дизайн как раз с планетами, но аватарки и другие изображения приходится делать плоскими, потому что img не применишь box-shadow: inset.
NMitra
Сделайте фоном background. Скоро благодаря поддержки трансформации CSS можно будет добавлять объём. Предвестники http://codepen.io/html5web/pen/pnbwo
Космо Мизраил
Мдо, вроде-бы для вебкита, а не работает х) Это будет вступать лет пять ещё, до этого надо ещё дожить

Фоны сделать не всегда получится, а вот наложить поверх изображения элемент с заданными стилями очень даже можно. Но это если известны размеры изображения.Пример: http://jsfiddle.net/9qzm6/

Ещё нашёл скрипт, который выполняет эту работу самостоятельно:http://www.htmldrive.net/items/demo/1156/Multiple-CSS3-Image-StylesЗдесь он сам определяет размер, если изображение загрузилось. Нужен jQuery.

Это так, на заметку
NMitra
Там нужны настройки какие-то устанавливать.. Это сильно вперёд:))

Пжалст я ваш постоянный читатель уже год как минимум
Анонимный
IE 11Все анимировано))
NMitra
Молодцом IE, дотянулось. Осталась Хрому убрать -webkit-, он теперь в числе отстающих.

Окружность

Циркуль — инструмент для черчения окружностей и дуг, также может быть использован для измерения расстояний.

окружность

Если установить ножку циркуля с иглой в какую-либо точку, а ножку с грифелем повернуть вокруг этой точки, у нас получится замкнутая линия. Она называется окружностью.

{"questions":[{"content":"На каких рисунках присутствуют окружности? Выберите все подходящие ответы:`img_choice-1`","widgets":{"img_choice-1":{"type":"img_choice","options":[["https://obrazavr.ru/wp-content/uploads/2023/05/nozhniczy-2.svg"],["https://obrazavr.ru/wp-content/uploads/2023/05/skrepki.svg"],["https://obrazavr.ru/wp-content/uploads/2022/07/keys.svg"],["https://obrazavr.ru/wp-content/uploads/2022/07/bicycle.svg"]],"answer":}}}]}

Основные отличия круга от круга

определения

обхват: круг – это замкнутая кривая, так что все точки кривой находятся на фиксированном расстоянии «r», называемом радиусом, от фиксированной точки «C», называемой центром круга.

круг: это область плоскости, которая ограничена окружностью, то есть все они являются точками внутри круга.

Можно также сказать, что круг – это все точки, которые меньше или равны «r» от точки «C».

Здесь вы можете заметить первое различие между этими понятиями, поскольку окружность – это только замкнутая кривая, а окружность – это область плоскости, окруженная окружностью..

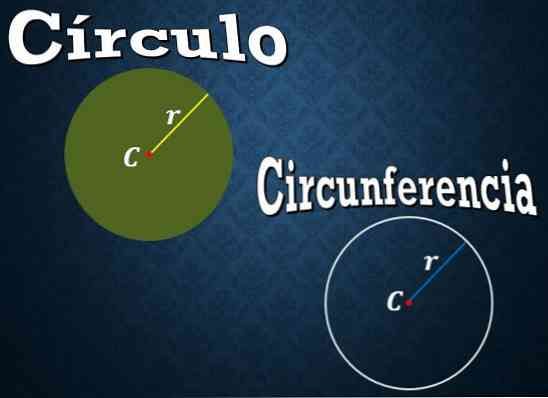
Декартовы уравнения

Декартово уравнение, представляющее окружность: (x-x0) ² + (y-y0) ² = r², где «x0» и «y0» – это декартовы координаты центра круга, а «r» – радиус.

С другой стороны, декартово уравнение окружности имеет вид (x-x0) ² + (y-y0) ² ≤ r² или (x-x0) ² + (y-y0) ²

Разница между уравнениями заключается в том, что по окружности это всегда равенство, а по кругу это неравенство.

Одним из следствий этого является то, что центр круга не принадлежит окружности, в то время как центр круга всегда принадлежит кругу.

Графики в декартовой плоскости

Из-за определений, упомянутых в пункте 1, вы можете видеть, что графики круга и круга:

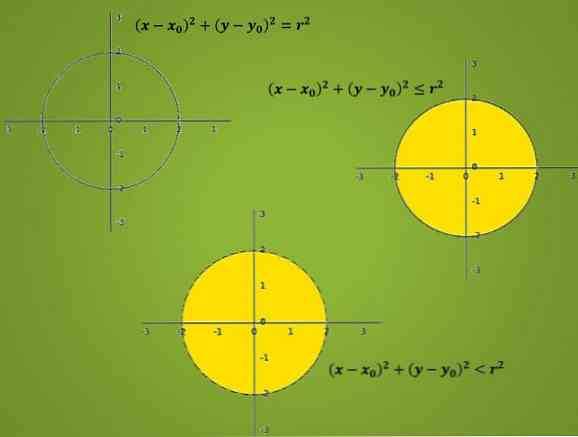
На изображениях вы можете увидеть разницу, которая была упомянута в пункте 1. Кроме того, проводится различие между двумя возможными декартовыми уравнениями круга. Когда неравенство строгое, край круга не включается в график.

размеры

Другое отличие, которое можно отметить, касается размеров этих двух объектов..

Поскольку окружность – это просто кривая, это одномерная фигура, поэтому она имеет только длину. Круг с другой стороны – это двумерная фигура, поэтому он имеет длинную и широкую поверхность, поэтому у него есть связанная область..

Длина круга радиуса “r” равна 2π * r, а площадь круга радиуса “r” равна π * r².

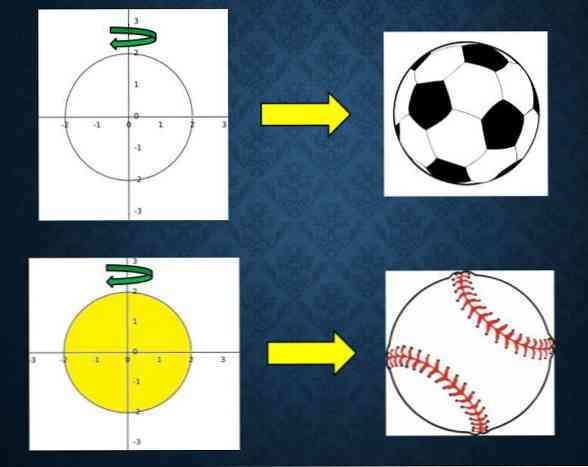
Трехмерные фигуры, которые генерируют

Если вы рассматриваете график круга, и он вращается вокруг линии, проходящей через его центр, вы получите трехмерный объект, который является сферой..

Следует отметить, что эта сфера полая, то есть это только край. Примером сферы является футбольный мяч, потому что внутри него есть только воздух.

С другой стороны, если ту же самую процедуру выполнить с кружком, будет получена сфера, но она заполнена, то есть сфера не является полой.

Примером этой заполненной сферы может быть бейсбол.

Следовательно, создаваемые трехмерные объекты зависят от того, используется ли окружность или круг.

ссылки

Басто, Дж. Р. (2014). Математика 3: Основная аналитическая геометрия. Патрия Редакционная группа.
Биллштейн Р., Либескинд С. и Лотт Дж. У. (2013). Математика: проблемный подход для учителей базового образования. Лопес Матеос Эдиторес.
Bult, B. & Hobbs, D. (2001). Математическая лексика (иллюстрированный ред.). (Ф. П. Кадена, Трад.) Издания АКАЛ.
Каллехо И., Агилера М., Мартинес Л. и Алдеа С. (1986). Математика Геометрия. Реформа верхнего цикла Э.Г.. Министерство образования.
Schneider, W. & Sappert, D. (1990). Практическое техническое руководство по рисованию: введение в основы промышленного технического рисования. Реверте.
Томас, Г. Б. и Вейр, М. Д. (2006). Расчет: несколько переменных. Пирсон Образование.

Выводы

Круг – плоская, двухмерная фигура. Шар – объемное трехмерное геометрическое тело. Тем не менее, они имеют массу сходств (наличие ограничивающей поверхности, диметра и радиуса, наполненность структуры в отличие от той же окружности, возможност вычислить площадь).

Чем же отличается круг от шара? Круг плоский, шар же имеет объем. Именно объемность шара позволяет ему делиться на сечения, которые по своей сути являются кругами. Круг, напротив, делится на сектора.

Публикации по теме:

Детско-родительский игровой сеанс «Круг» для детей ОВЗ Игровое занятие КРУГ для детей ОВЗ Тема «Осень. Природные явления» Цели и задачи занятия КРУГ Главная цель занятия КРУГ – дать каждому ребенку.

Конкурс профессионального мастерства «Солнечный круг» (фотоотчет) С 12 по 26 октября 2015 года в нашем детском саду проходил конкурс профессионального мастерства «Воспитатель года». Цель конкурса: выявление.

Конспект НОД по ФЭМП «Знакомьтесь: круг» Конспект НОД по ФЭМП во второй младшей группе «Знакомьтесь- круг» Цель: развитие познавательных интересов детей Задачи: Познакомить.

НОД по математике «Круг и квадрат» (младшая группа) Тема: «Круг и квадрат» (младшая группа) Образовательная область: познание Цель: Продолжать учить находить один и много предметов в специально.

Поделки в технике «объемный квиллинг» Здравствуйте, коллеги! Недавно открыла для себя технику объемного квиллинга. Искусство, которое на русском языке называют «бумагокручением»,.

Проект по математическому развитию «Круг, квадрат и треугольник-фигуры важные, фигуры нужные» Номинация проекта – «Дошкольный возраст» Вид проекта: долгосрочный, фронтальный. Участники проекта: подгруппа детей средней группы, воспитатель.

«Снежинка 3-D». Объемный модуль для украшения интерьера Приближаются Новогодние праздники и перед нами, как воспитателями опять стоит вопрос «Чем же удивить детей и взрослых?». Просторы Интернета.

Совместная образовательная деятельность по ФЭМП «Круг и квадрат» Совместная образовательная деятельность взрослого и детей ФЭМП «Круг и квадрат». Цель: закреплять умение различать и называть круг и квадрат.

Весенний объемный тюльпан на открытке в подарок маме Не за горами прекрасный весенний праздник 8 Марта. И уже сейчас многие педагоги задумались над тем, что бы смастерить с детьми мамам в.

На уроках геометрии в школе все мы изучали свойства различных фигур и линий. Каждая из них имеет свои особенности, а порой некоторые из них взаимосвязаны друг с другом. Взять для примера хотя бы круг и окружность – между ними есть определенная связующая линия. Только вот какая? Давайте вместе разберемся в этом вопросе.Окружность
представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности. Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность. Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится. По этой причине имеется четкое понятие, что окружность делит всю плоскость на две части – внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, поскольку плоскость в общем понимании не имеет границ.Круг
является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность. Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.
Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии. Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга. Иными словами, круг представляет собой не только окружность, которая является его границей, но также и то бесконечное число точек, находящихся внутри этой окружности.

Выводы

Да, тема о круге и окружности (что это такое) очень проста для понимания. Но вообще все то, что касается этих геометрических фигур, является самым сложным для изучения. Школьнику нужно быть готовым к тому, что круг – фигура капризная. Но, как говорится, тяжело в учении – легко в бою. Да, геометрия – наука сложная. Зато успешное ее освоение позволяет сделать маленький шажок в сторону успеха. Потому что старания при обучении позволяют не только пополнять багаж собственных знаний, но и получать необходимые в жизни навыки. Собственно, на это и нацелена школа. А ответ на вопрос о том, что такое окружность и круг, является вторичным, хоть и важным.

http://onlinerepetitor.net/article/chem-otlichaetsya-krug-ot-okruzhnostihttp://moluch.ru/archive/132/55020/http://fb.ru/article/221626/chto-takoe-okrujnost-i-krug-v-chem-ih-otlichiya-i-primeryi-dannyih-figur-iz-jizni