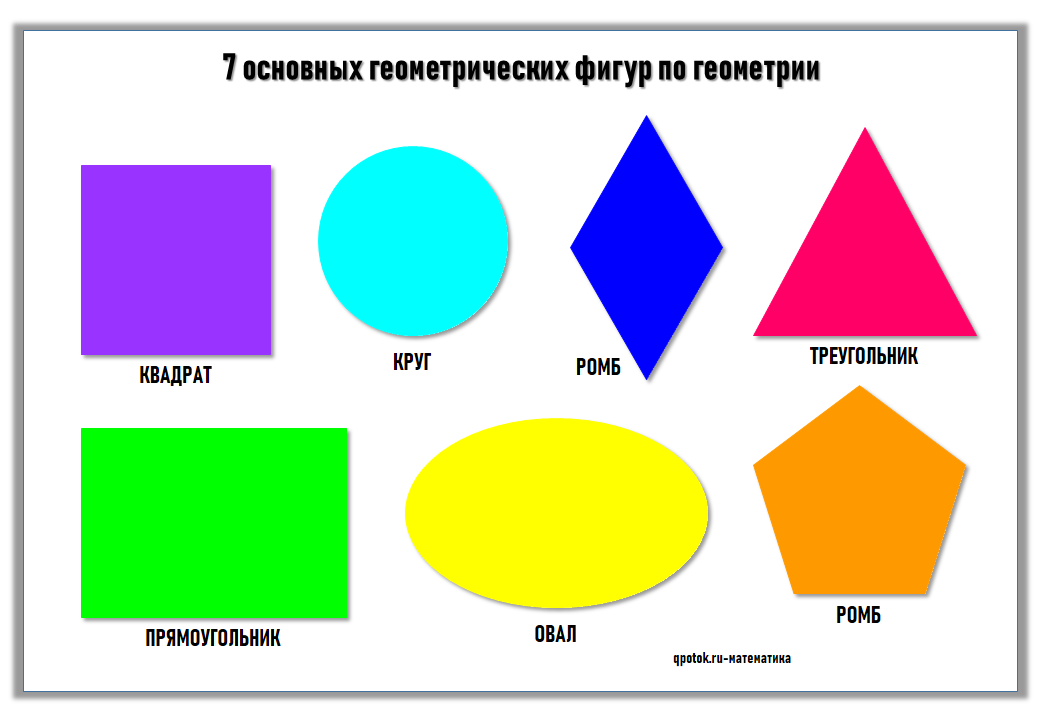
Что такое овал?
Овал часто используется в графике и дизайне, так как его форма является эстетически привлекательной и интересной для глаза. Он также является математическим объектом изучения в области аналитической геометрии.
Размеры овала могут быть различными — от почти круглой формы до значительно вытянутого или сплюснутого в одну из сторон. Овал может быть симметричным или асимметричным, что дает дизайнерам и художникам большую свободу выразить свою творческую идею. В зависимости от конкретной формы овала, его можно использовать для создания органических, мягких и приятных изображений, или, наоборот, для создания динамических и энергичных композиций.
Таким образом, овал — это важный элемент в графике, дизайне и математике. Его форма и размеры позволяют создавать разнообразные и привлекательные изображения, а его изучение помогает понять основные принципы аналитической геометрии и графики.
Определение овала в геометрии
Графика и математика тесно связаны в определении овала в геометрии. Овал можно представить на плоскости с помощью математической формулы, которая описывает его размеры и форму.
Овал можно использовать в различных областях, включая дизайн, искусство и архитектуру. Его форма может быть привлекательной и гармоничной, что делает его популярным элементом в создании различных произведений и объектов.
Геометрический овал имеет особенности, поэтому важно учитывать эти особенности при работе с ним. Например, при построении овала на плоскости нужно учитывать его размеры и соотношение сторон, чтобы сохранить его овальную форму
Таким образом, определение овала в геометрии включает его графическое представление, математическую формулу, его особенности и применение
Овал является уникальной фигурой, которая может привлекать внимание и быть использована в создании разнообразных объектов и произведений
Особенности формы овала
В отличие от эллипса, овал имеет меньший размер и менее симметричную форму. Форма овала обычно описывается как сочетание двух радиусов, ширины и высоты. Овал может быть как вертикальным, так и горизонтальным, в зависимости от ориентации его осей.
Овал часто используется в дизайне, чтобы создать эффект движения или интригующую композицию. Узкая и длинная форма овала может быть использована в качестве фонового элемента или рамки для текста или изображений. Эта форма также может добавить интерес к простым формам, таким как круги или квадраты, и создать контраст с геометрическими линиями.
Овал также используется в проектировании интерфейсов пользовательских приложений. Он может быть использован как кнопка или иконка, добавляющая мягкость и гармонию в визуальном мире электронных устройств.
Графические программы обычно предлагают инструменты для создания овала, и это удобно, так как форма овала может быть сложна для создания вручную. Овал требует более тонкого и аккуратного подхода, чем эллипс, чтобы сохранить его характерные особенности.
Основные особенности формы овала:
- Более широкое и плоское область в центре и более узкие края;
- Меньший размер по сравнению с эллипсом;
- Меньшая симметрия;
- Возможность изменять ориентацию осей;
- Мягкость и гармония, которые овал приносит в дизайн.
Таким образом, форма овала представляет собой интересный элемент графики и дизайна с его уникальными особенностями и возможностями для творческой реализации.
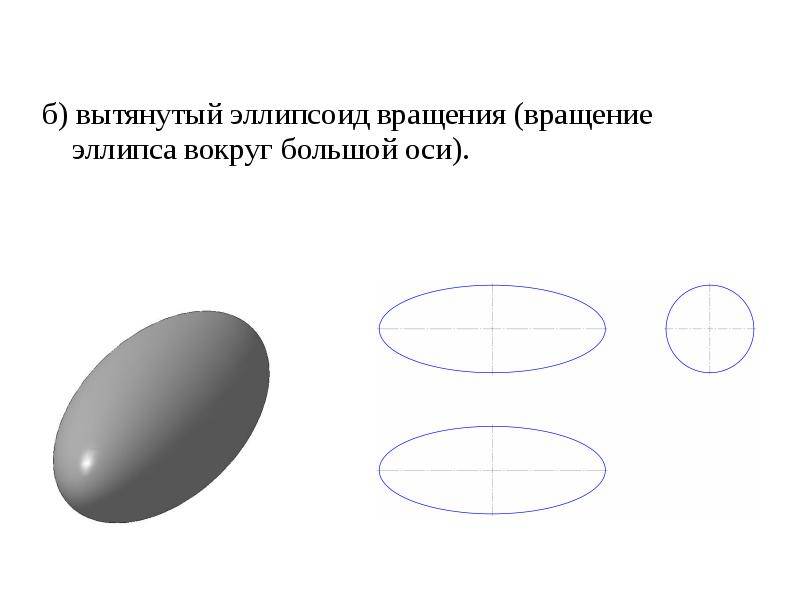
А как насчет трехмерных геометрических фигур?
Существуют также трехмерные формы, которые имеют не только длину и ширину, но также глубину или объем. Это формы, которые вы видите в реальном мире, такие как сферический баскетбольный мяч, цилиндрический контейнер с овсянкой или прямоугольная книга.
Трехмерные формы, естественно, более сложные, чем двухмерные, с дополнительное измерение – количество места, которое они занимают, а не только форма, – которое необходимо учитывать при расчете площади и периметра.
Математика, включающая двумерные фигуры, подобные приведенным выше, называется плоская геометрия, потому что она имеет дело с плоскостями или плоскими формами. Математика, включающая трехмерные формы, такие как сферы и кубы, называется сплошная геометрия, потому что она имеет дело с твердыми телами, другим словом для трехмерных форм.
2D-формы составляют 3D-фигуры, которые мы видим каждый день!
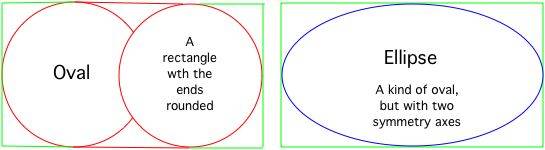
В чем различие?
Официальные определения каждой из фигур звучат достаточно сложно и непонятно.
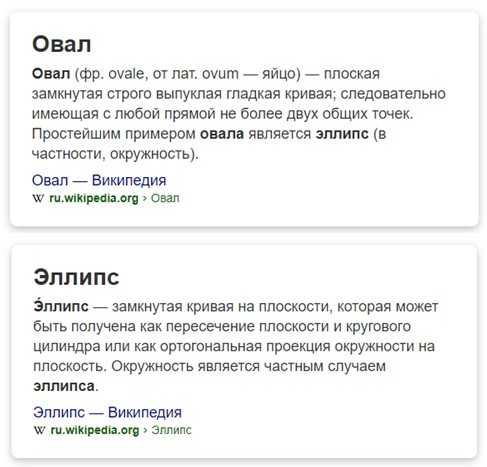
Но, если откинуть заумные формулы и сложные определения — все намного проще.
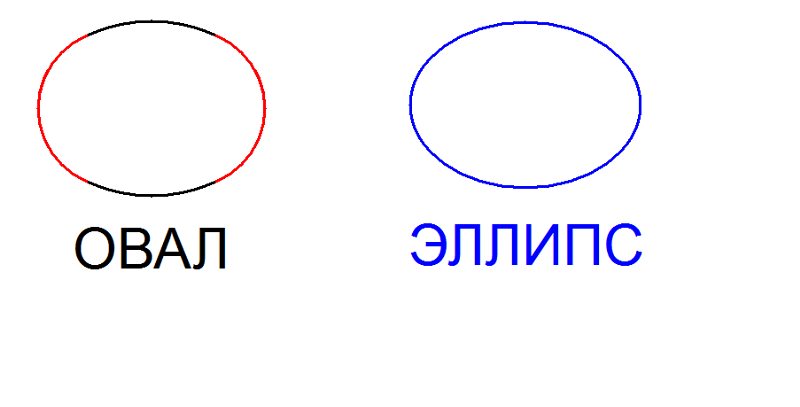
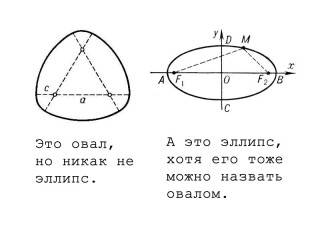
Овал можно «растянуть» как угодно. Это может быть практически круг, либо узкая и длинная замкнутая кривая — главное, чтобы ее форма удовлетворяла определению.
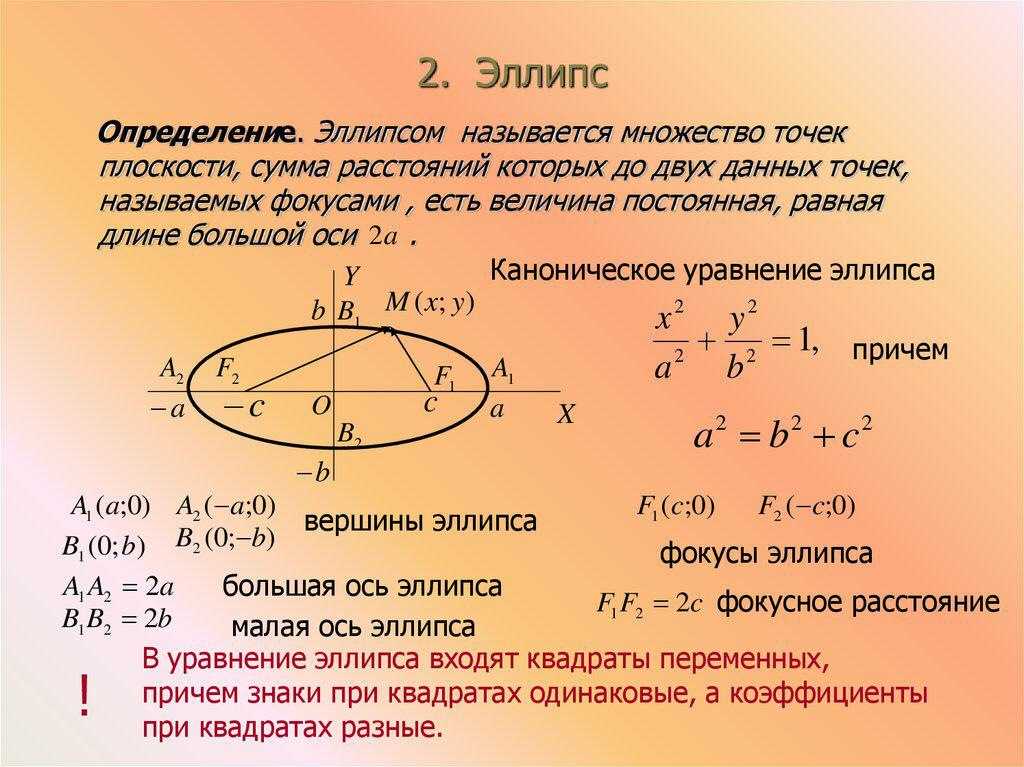
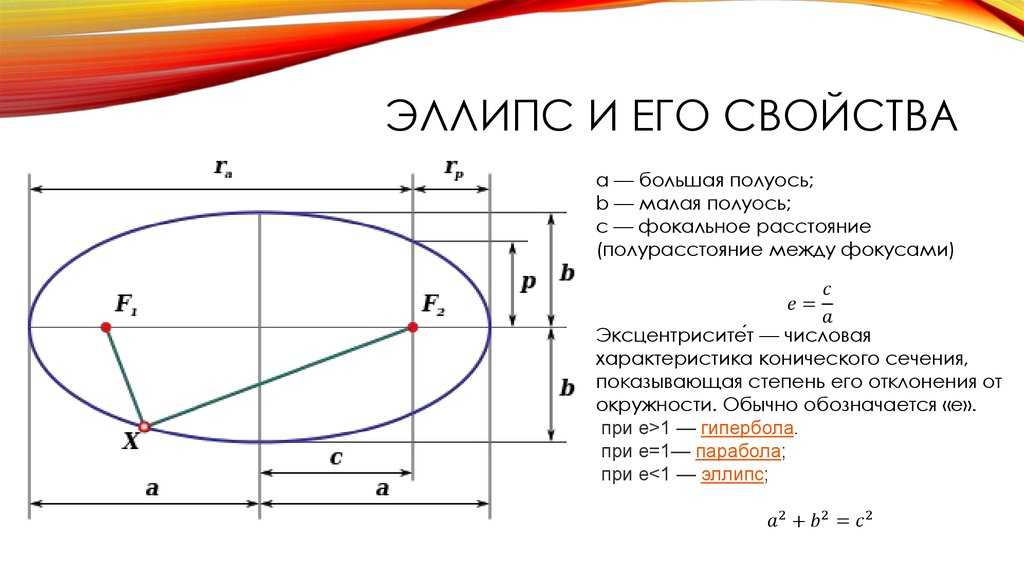
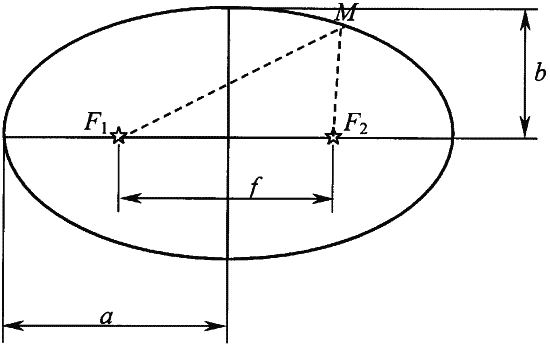
Эллипс — это «правильный» овал. Его пропорции строго регламентированы. Длины осей должны соответствовать уравнению: a2=b2+c2.
Где а — это длинная полуось, b — короткая, а с — фокальное расстояние (от центра до фокуса).
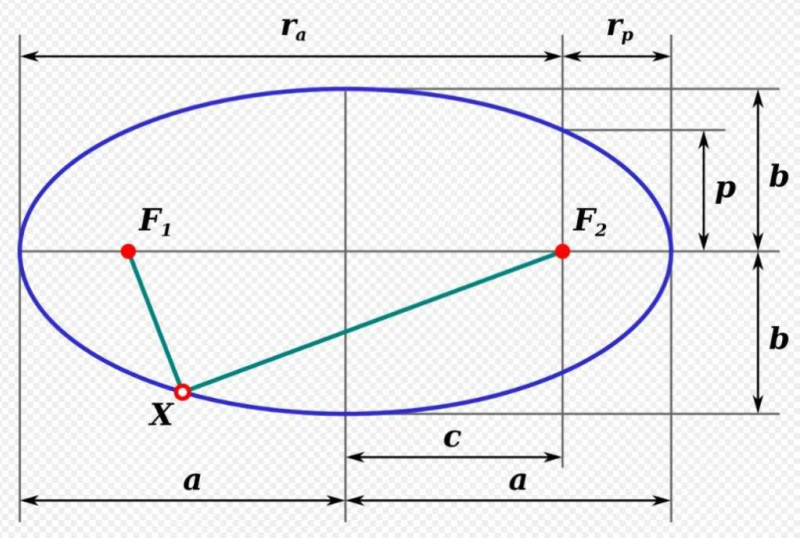
Всем известный круг — это частный вариант эллипса. В этом случае с=0 (т.к. фокус у него один). Полуоси (радиусы) тоже равны.
Что такое овал?
Овал – это фигура, которая имеет форму закругленного прямоугольника или эллипса.
Основная разница между овалом и эллипсом заключается в их пропорциях и форме:
- Форма: Овал обычно выглядит как эллипс, но с неравными равными радиусами и более закругленными углами.
- Пропорции: У овала более равные радиусы, в то время как у эллипса радиусы могут быть различными.
Овал является более общим термином, который может использоваться для описания различных фигур с закругленными углами. Геометрический овал может иметь прямоугольную форму или быть близким к форме эллипса.
При изучении геометрии овалы часто описывают с использованием фокусов – точек, расположенных на оси овала. Овалы могут быть использованы в различных областях, включая дизайн, искусство и архитектуру.
Описание овала
Овал — это геометрическая фигура, в которой по форме происходит смешение эллипса и круга. Он обладает двумя основными свойствами — осью и пропорциями.
В отличие от круга, овал имеет разные пропорции по длине и ширине. Ось овала — это линия, которая проходит через центр фигуры и соединяет две противоположные точки на ее границе. Ось разделяет овал на две равные половины, которые зеркально отражаются друг относительно друга.
Разница между овалом и эллипсом заключается в пропорциях и симметрии. Как уже упоминалось, овал имеет неравные пропорции, тогда как эллипс имеет равные пропорции по длине и ширине. Кроме того, овал не обладает такой же степенью симметрии, как эллипс.
Овал имеет два фокуса, которые расположены на его оси. Фокусы — это точки, в которых сосредоточена наибольшая энергия или притяжение. В овале фокусы находятся на равном расстоянии от центра и от оси фигуры.
В целом, овал является интересной геометрической фигурой, которая отличается от эллипса своими пропорциями и расположением фокусов.
Основные характеристики овала
Овал — геометрическая фигура, которая находится между окружностью и эллипсом. В отличие от эллипса, овал имеет две равные оси, а его пропорции не обязательно симметричны.
Оси: Овал имеет две оси — главную (большую) и побочную (меньшую). Главная ось делит овал на две одинаковые половины, а побочная ось перпендикулярна главной и симметрично делит овал.
Геометрия: Овал является замкнутой кривой линией, состоящей из части эллипса и части окружности. Это значит, что овал может быть описан как комбинация двух кривых линий.
Пропорции: Пропорции овала могут быть несимметричными, в отличие от эллипса, который всегда имеет симметричную форму. Это означает, что верхняя и нижняя части овала могут быть разного размера или формы.
Разница с эллипсом: Овал и эллипс являются похожими фигурами, но имеют некоторые отличия. В отличие от эллипса, овал имеет две равные оси и может иметь несимметричные пропорции. Эллипс же имеет две равные и симметричные оси с точками, которые отстоят от центра на одинаковое расстояние.
Примеры использования овала:
- Овалы используются для создания красивых и эстетичных дизайнов, особенно в мире моды и дизайна интерьеров.
- Овалы могут быть использованы для создания уникальных форм и контуров в живописи и графическом дизайне.
- Овалы могут быть использованы как элементы украшения или орнамента в архитектуре и декоративном искусстве.
Как рисовать правильные овалы
«Ни каких рыбок и сосисок! Надо рисовать правильные овалы! »
Именно так говорил мой преподаватель — Сергей Иванович Полуйчик, когда смотрел наши первые натюрморты. Благодаря этой фразе, я сразу запомнила, как должны выглядеть правильные овалы при построении цилиндрических форм.
Итак, знакомимся с рыбками, сосисками, и правильными овалами.
РЫБКА — неправильный овал с острыми углами.
Овал — это круг, который лежит на плоскости, поэтому с какой бы стороны мы не смотрели, у него не может быть острых углов.
СОСИСКА — неправильно нарисованный овал с параллельными сторонами.
Еще раз чтобы запомнилось: овал — это круг на плоскости, у круга нет параллельных сторон.
ПРАВИЛЬНЫЙ ОВАЛ, без острых углов и параллельных сторон.
Соблюдая правила перспективы, дальняя часть овала рисуется меньше (красная линия), ближняя к зрителю — больше (синяя линия на рисунке).
Практически все цилиндрические и конусовидные формы (кувшины, крынки, вазы, бутыли, кружки и т.д.) рисуются по одинаковой схеме. Вот, на примере этого кувшинчика и разберем пошагово эту схему рисования цилиндрических тел. Всё построение делается легкими, еле заметными линиями, чтобы не пришлось стирать резинкой, так как при стирании портится верхний слой бумаги. И краска в живописи, и штрихи в рисунке ложатся на бумагу после стирания неровно. |
 Определяем место предмета на листе. Проводим центральную осевую линию для построения кувшина. |
Определяем место осевых линий для построения овалов. То есть — с помощью метода визирования, уточняем пропорции и размеры между центрами овалов у кувшина. Проводим эти линии. |
С помощью визирования определяем размер овалов. Откладываем этот размер с помощью карандаша, отмечаем одинаковые отрезки от точки пересечения центровых линий. Откладываем точки ширины овалов. Отмечая эти размеры не забываем о правилах перспективы: та сторона овала, что дальше от нас — будет чуточку меньше, значит та, что ближе к нам — больше. Точно также помним, чем ниже уровня глаз находится овал, тем сильнее ему хочется стать кругом. |
Наконец-то прорисовываем овалы нашего цилиндрического предмета. |
Соединяем крайние точки овалов и наш кувшин практически готов. Осталось дорисовать ручку и носик. При рисовании ручки и носика, стараемся помнить, что обычно они находятся напротив друг друга, то есть на одной линии. |
КАК РИСОВАТЬ ОВАЛЫ В ЗАВИСИМОСТИ ОТ УРОВНЯ ГЛАЗ ХУДОЖНИКА Так будет выглядеть построение кувшина, если мы поставим его повыше, чем тот, построение которого мы разбирали. |
Так будет выглядеть построение кувшина, если верхняя кромка кувшина будет находиться на уровне глаз, поэтому изображаем в виде линии. Но дно-то кувшина, ниже уровня глаз, поэтому, чтобы увидеть линию дна — строим для дна овал. рисуем кувшин выше уровня глаз |
Так будет выглядеть построение кувшина, если его середина будет совпадать с линией глаз. Верхняя часть кувшина будет выше линии глаз — рисуем овал, у которого ближе к нам будет верхняя линия. Дно кувшина получается немного ниже уровня глаз, потому строим обычный овал. Но! Если кувшин (ваза) стоит далеко от зрителя (художника), то и верхний край и линия дна будут рисоваться простой прямой линией, как будто находятся на уровне глаз. Начинающие художники очень часто допускают ошибки именно при построении овалов, от чего портится впечатление от всей картины в целом. |
www.mogut-vse.ru
Овал: геометрические характеристики
Овал — это плоская фигура, которая представляет собой замкнутую кривую линию, имеющую форму, близкую к эллипсу, но не являющуюся точно эллипсом. Овал имеет некоторые характеристические черты, которые позволяют его отличить от эллипса и других фигур.
Главные геометрические характеристики овала включают:
- Длина: это периметр овала — сумма всех сторон фигуры. Для регулярного овала (в котором все стороны и углы равны) длина может быть вычислена как произведение половины суммы большой и малой осей (a и b) на число пи (π).
- Площадь: это количество плоской площади, ограниченной овалом. Для регулярного овала площадь может быть вычислена как произведение половины большой оси (a) и половины малой оси (b) на число пи (π).
- Оси: овал имеет две оси — большую (a) и малую (b). Большая ось — это самая длинная прямая линия, проходящая через центр овала и образующая его длину. Малая ось — это прямая линия, перпендикулярная большой оси и образующая его ширину.
Кроме того, овал может иметь центр — точку, которая делит его на две равные части и находится в середине его большой и малой осей.
Вместе эти характеристики помогают определить форму овала и отличить его от других фигур, таких как круг или эллипс.
Использование в дизайне и искусстве
Эллипс, с его симметричной и органической формой, может придать дизайну ощущение гармонии и уравновешенности. Он может использоваться для создания закругленных и мягких контуров, что создает впечатление комфорта и спокойствия. Эллипсы часто используются в логотипах, упаковках и веб-дизайне.
Овал, с его более длинным и вытянутым видом, может служить для создания чувства движения и динамизма. Овалы могут быть использованы для подчеркивания направления или придания энергии композиции. Использование овалов в искусстве и дизайне может добавить визуальный интерес и уникальность.
Кроме того, эллипсы и овалы могут быть использованы в качестве каркасных элементов для размещения содержимого. Они могут служить рамками или фонами для текста, изображений или других объектов. Использование этих фигур в дизайне помогает создать упорядоченное и структурированное пространство.
Таким образом, эллипсы и овалы представляют собой важные инструменты для дизайнеров и художников, которые помогают создать интересные и привлекательные композиции. Их использование может добавить гармонии, движения и уникальности в любой проект или произведение искусства.
TheDifference.ru определил, что отличие овала от эллипса заключается в следующем:
Свойства. У эллипса сумма расстояний от двух фокусов, лежащих на большой оси, до точки на кривой, является одинаковым и равно длине центральной оси.
Выполняя сложные, многоярусные потолки из гипсокартона, часто возникает необходимость сделать овал. Он может выглядеть в виде выреза на потолке из гипсокартона, либо же опускаться на ярус ниже, в любом случае, чтобы сделать овал на потолке, его сначала необходимо нарисовать. Это не круг, который можно начертить при помощи самопального циркуля из профиля. Чтобы нарисовать овал, нужны более сложные расчёты и знания геометрии. В принципе, есть два вида овалов. Правильный, и не правильный. На глаз их различить практически не возможно.
Первый способ как начертить овал.
Не правильный овал можно начертить вписав его в ромб. Для этого в нужном месте, чертим оси координат и рисуем равносторонний ромб нужного нам размера. Теперь рисуем две дуги с центром в двух противоположных углах ромба. Радиус этой дуги можно вычислить следующим образом. С вершины ромба опускаем перпендикуляры к двум противолежащим сторонам ромба. Длинна этих перпендикуляров и есть радиус необходимых нам дуг. На рисунке, перпендикуляры нарисованы чёрным цветом, а получившиеся дуги синим.
Тоже самое проделываем и с противоположной вершиной ромба. В точках пересечения перпендикуляров, мы получаем ещё два центра для построения двух оставшихся дуг. Радиус этих дуг (на рисунке начерчено красным) не трудно будет вымерить, когда все необходимые линии будут уже начерчены.
Второй способ как нарисовать овал
Если фигура нужна менее точная (приблизительная), то начертить овал можно при помощи нитки, двух саморезов и карандаша. Для этого, нужно будет найти так называемые фокусы овала. Это как раз те точки, относительно которых мы рисовали последние две дуги. На рисунке выше, они показаны красным цветом. В эти точки фокусов, вкручиваем два самореза и привязываем к ним нить. Нить нужно подобрать такую, чтобы она не тянулась. Длинна нити, равна большему размеру овала. Теперь всё просто, карандашом натягиваем нить, и рисуем овал.
Чёткий овал нарисовать таким способом вы конечно не сможете, нить тянется, да и карандаш ровно удержать трудно. Такой овал немного придётся корректировать. Если овал большой, то погрешностей не увидит и тот, кто знает о них. Если маленький, то нарисовать овал лучше циркулем.
геометрический овал с одной осью симметрии
Принципы рисования эллипсов:
Принцип 1. У эллипса есть две оси симметрии: большая и малая. Они перпендикулярны. Здесь будем работать с наиболее частым случаем – когда предмет расположен прямо, то есть вертикальная ось (малая) находится под углом в 90°, а горизонтальная (большая) – под углом в 180°.

Принцип 2. У эллипса 4 вершины (они лежат на пересечении с осями). Эти точки в наибольшей степени удалены от центра. Форма эллипса выглядит искаженной, если соседние с вершинами точки смещены на тот же уровень (на эллипсе справа показано красным цветом).

Принцип 3. Другая крайность – это заострение боков эллипсов. Они должны быть скругленными. В бока можно вписать окружности. И чем больше раскрыт эллипс, тем больше диаметр этой окружности относительно высоты эллипса (на примере ниже это сравнение показано бледно-голубым цветом).
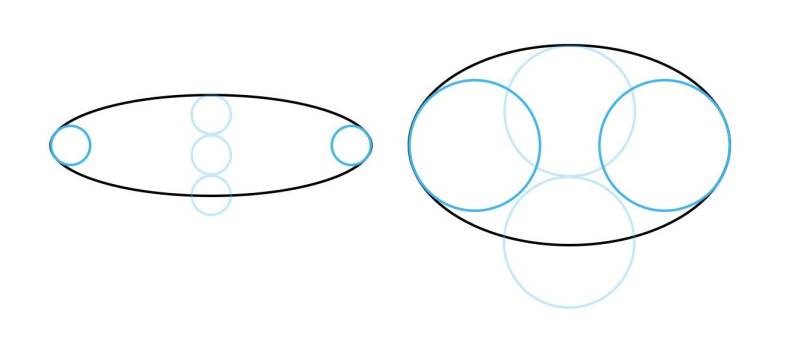
Принцип 4. Центр эллипса смещен вдаль (вверх) относительно геометрического центра из-за перспективного искажения. То есть ближняя половина эллипса больше дальней
Однако обратите внимание, что это смещение очень незначительно. Разберем, почему
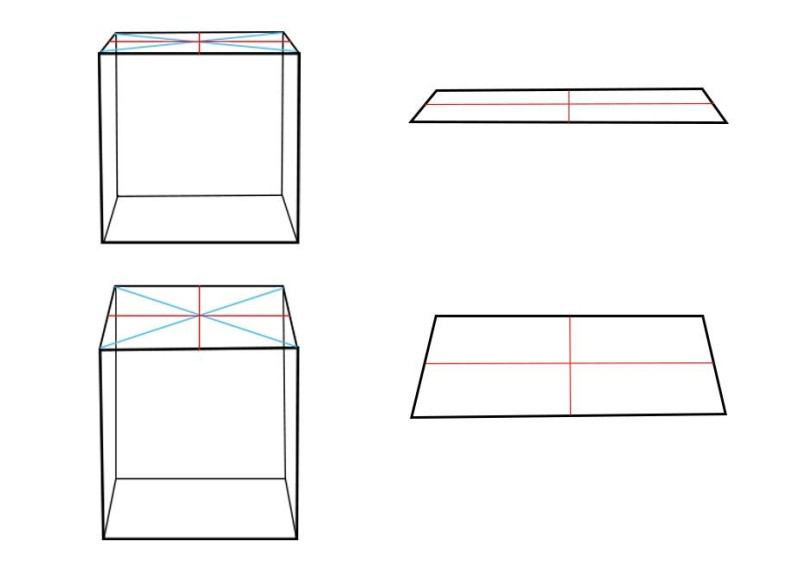
Начнем с квадратов, поскольку круг вписывается в эту форму. Ниже показаны кубы, справа их верхние квадратные грани в перспективе. Проведены оси красным. Сравните, насколько их ближние половины больше дальних. Разница очень небольшая. То же самое будет и для эллипсов, вписанных в них. Ошибочно преувеличивать в рисунках эту разницу между ближней и дальней половинками эллипсов.
Эллипс
Из основных характеристик эллипса следует упомянуть его уравнение. Алгоритм для определения уравнения эллипса основан на расстоянии от фокуса до точки кривой. Эллипс выделяется своими фокусами, точками на кривой, для которых сумма расстояний до фокусов постоянна.
Визуально эллипс может быть похож на овал, но между ними есть разница. Овал — это парабола с вытянутой осью, тогда как эллипс имеет две симметричные оси. Овал обычно более широкий и плавный, чем эллипс, поэтому эллипс часто считается более симметричной и уравновешенной формой.
Зная характеристики эллипса, можно проводить различные геометрические операции с ним. Например, построение линии, проходящей через фокусы эллипса, или нахождение пересечений с другими геометрическими фигурами.
Таким образом, эллипс является одной из важных геометрических фигур, имеющей свои особенности и характеристики. Разница между овалом и эллипсом заключается в их форме, симметрии и уравнении.
Основные характеристики эллипса
Эллипс можно назвать удлиненным овалом или овалом симметрии. Главная разница между эллипсом и овалом заключается в основной линии фигуры. У эллипса основная линия называется большой полуосью (а), а у овала это второстепенная линия.
Одна из основных характеристик эллипса — его эксцентриситет. Эксцентриситет эллипса определяет его плоскость, его форму. Чем ближе эксцентриситет к нулю, тем более круглым будет эллипс, а чем ближе к единице, тем более вытянутым будет эллипс.
Другая важная характеристика — фокусные точки эллипса. Фокусные точки это две точки внутри эллипса, для которых сумма расстояний до любой точки на эллипсе всегда одинакова. Если обозначить эти точки как F1 и F2, то для любой точки на эллипсе A, сумма расстояний AF1 и AF2 всегда будет одинаковой.
Эллипс также имеет основные оси. Большая полуось (а) является самой длинной линией эллипса, проходящей через его центр. Меньшая полуось (b) является самой короткой линией, перпендикулярной большой полуоси и проходящей через центр эллипса.
Важно отметить, что овал является частным случаем эллипса, когда его эксцентриситет равен единице
| Название | Описание |
|---|---|
| Эксцентриситет | Определяет форму эллипса |
| Фокусные точки | Две точки внутри эллипса с одинаковой суммой расстояний до эллипса |
| Большая полуось | Самая длинная линия, проходящая через центр эллипса |
| Меньшая полуось | Самая короткая линия, перпендикулярная большой полуоси и проходящая через центр эллипса |
Форма и структура эллипса
Главная разница между овалом и эллипсом заключается в том, что овал является формой, в которой все линии огибаются равными расстояниями от центра. В то же время, эллипс — это форма, в которой есть два фокуса, вокруг которых линии огибаются с разными расстояниями.
У эллипса есть математическое уравнение, известное как уравнение эллипса, которое определяет его форму и расположение на графике. Также существует алгоритм для рисования эллипса, который позволяет точно нарисовать его форму на основе его уравнения.
Таким образом, форма и структура эллипса имеют определенные особенности, отличающие его от овала
Это важно учитывать при рассмотрении и использовании этих геометрических фигур в различных областях науки и практики
Примеры использования эллипса
- В архитектуре эллипсы часто используются для создания оригинальных форм зданий. Одним из известных примеров использования эллипса в архитектуре является стадион «Маракана» в Бразилии, где форма стадиона представляет собой эллипс.
- В геодезии эллипсы используются для моделирования формы Земли и ее отклонений от сферы. Геоид — это эллипсоид, который представляет собой модель формы Земли, учитывающую ее геометрические отклонения и распределение массы.
- В оптике эллипсы используются для описания формы линз и заземления света. Линзы с эллиптической формой позволяют менять фокусное расстояние и фокусировать световые лучи в разных точках.
- В астрономии эллипсы используются для описания формы галактик. Галактики эллиптической формы имеют характерное эллиптическое распределение звезд и отличаются от спиральных галактик.
Таким образом, разница между овалом и эллипсом заключается в их характеристиках и использовании. Овал — это произвольная фигура без явно определенной формы, в то время как эллипс имеет строго определенные параметры и уравнение.
Comparison Table
| Parameters of Comparison | Circle | Ellipse |
|---|---|---|
| Definition | It is a round-shaped mathematical figure with the same distance from any point on the circumference to the center. | It is a mathematical figure where a curve is drawn over a plane both ways to give a flattened circular shape. |
| Area | π × r^2 ( r = radius ) | π × a × b |
| Definite shape | It has a definite shape of a round figure. | It may vary from the surface towards a more flattened structure of an ellipse. |
| Distance from center | It has the same distance from the center to any point in the circumference. | It does not have the same distance from the center. |
| Components of figures | One radius at the center. | It has two foci that lie at either end of the ellipse. |
Похожие вопросы
Геометрия 31.12.2018 17:11 16 Любимова Даринка
как определить в какой точке касаются эллипс и окружность?Уровнение элипса Х2/16 + у2/4=1, уравнение
Ответов: 1
Геометрия 06.02.2021 11:24 13 Полетаева Вика
Мне нужно построить усеченную сферу на плоскости 120 градусов. Как строить эллипс знаю, но для постр
Ответов: 1
Геометрия 25.02.2019 21:31 12 Щербинина Наталья
Определите окружность овала(70на 45). Именно окружность, НЕ площадь! И напишите, пожалуйста, как вы
Ответов: 1
Геометрия 19.05.2019 10:44 30 Поляк Настя
Можно ли правильный многоугольник с числом сторон большим, чем у квадрата, вписать в эллипс, чтобы е
Ответов: 1
Геометрия 15.06.2018 04:22 31 Толстобров Никита
Где в жизни или в науке используется эллипс
Ответов: 1
Геометрия 18.07.2018 11:55 25 Кусь Арина
Тест по теме «Симметрия (Планиметрия)». 1.Какая фигура не обладает осевой симметрией? а) квадрат; в)
Ответов: 1
Геометрия 28.11.2018 20:23 26 Паночишена Діана
Какая фигура является основанием цилиндра: а) окружность; б) круг; в) эллипс
Ответов: 1
Геометрия 05.01.2019 01:31 13 Емельянов Паша
1. Составить уравнение окружности и построить ее.2. Составить уравнение окружности с центром в точке
Ответов: 1
Геометрия 12.02.2019 00:53 11 Далглыджева Дарья
Эллипс в жизни . историческая справка.
Ответов: 1
Геометрия 09.03.2019 15:45 7 Абгарян Армен
Где можно встретить в жизни эллипс,парабола,гипербола?
Ответов: 1
Геометрическое определение
Эллипс — это геометрическая фигура, у которой длины двух радиусов не равны. Фокусные линии эллипса также не пересекаются в его центре и имеют разные длины. Фокусные линии эллипса представляют собой отрезки, соединяющие его два фокуса.
Таким образом, основное отличие между овалом и эллипсом заключается в их геометрических свойствах. Овал — это фигура с равными длинами радиусов и фокусными линиями, пересекающимися в его центре, в то время как эллипс имеет неравные длины радиусов и фокусные линии, которые не пересекаются в его центре.
Овал
Эллипс – это плоская геометрическая фигура, состоящая из всех точек, для которых сумма расстояний до двух точек, называемых фокусами, постоянная величина. Овал же – это именно форма эллипса, которая является более широкой и симметричной.
Если проводить соотношение с кругом, то овал может иметь разные длины осей, в то время как у круга все оси будут одинаковой длины.
Один из важных элементов овала – это фокусные линии. Каждая фокусная линия проходит через фокус овала. Фокусные линии не обязательно должны быть одинаковой длины и могут быть разного угла наклона.
Таким образом, овал является более широкой и симметричной формой эллипса, которая может иметь разные длины осей и фокусные линии.
Эллипс
Овал и эллипс имеют похожую форму, их основное различие заключается в соотношении длины осей. В овале нет геометрического определения, но обычно овалом называют фигуру с несколько более протяженными кривизнами, или с одной из осей большей, чем у диаметра эллипса.
Эллипс можно получить, поменяв местами значения двух радиусов при построении круга. Если радиус по оси X больше радиуса по оси Y, то получится вертикальный эллипс. Если радиус по оси Y больше радиуса по оси X, то получится горизонтальный эллипс.
Важно отметить, что эллипс является общим случаем для круга, что означает, что эллипс является просто закрытой кривой площадью, равной площади круга
4. Овал в геометрии
Так же, как в обыденной речи, в геометрии математический термин “овал” встречается в названиях различных геометрических фигур более или менее овальной формы, но без точного определения овала как такового. Общее между этими кривыми, что это обычно кривые замкнутые, выпуклые, гладкие (с касательной в любой точке) и имеют по крайней мере одну ось симметрии.
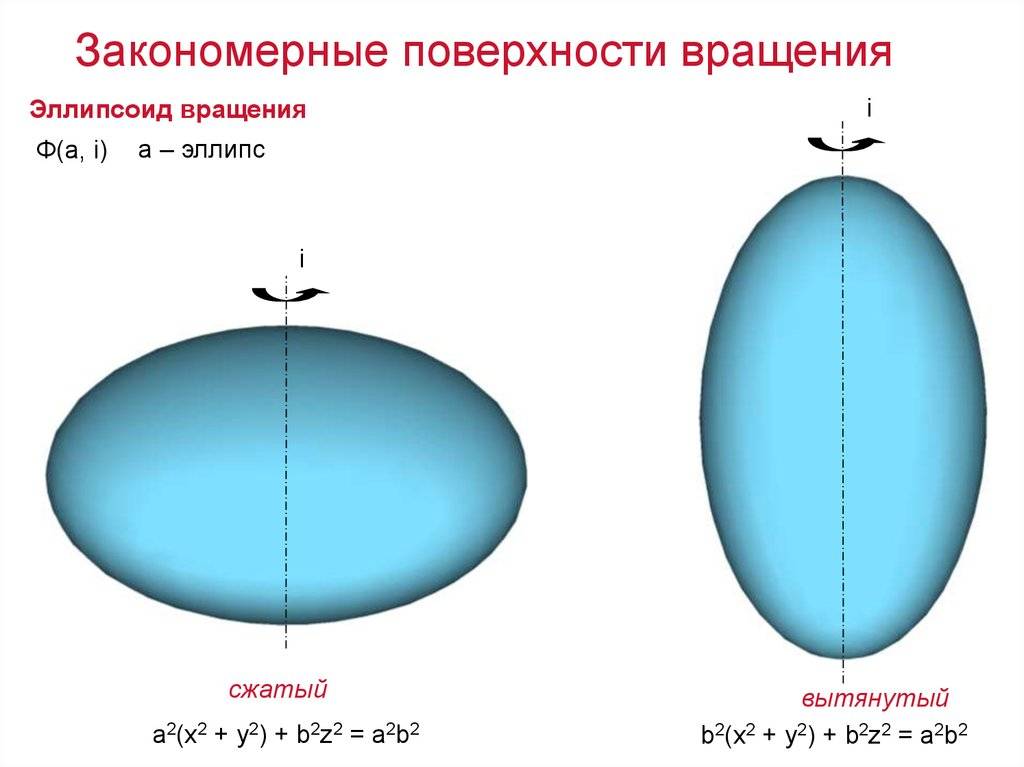
Термин “овалоид” употребляют в яйцевидных поверхностей образованных вращением овальной кривой вокруг одной из ее осей симметрии.
Другие примеров овалов можно отнести.
Овал
– это замкнутая коробовая кривая, имеющая две оси симметрии и состоящая из двух опорных окружностей одинакового диаметра, внутренне сопряженных дугами (рис. 13.45). Овал характеризуется тремя параметрами: длина, ширина и радиус овала. Иногда задают только длину и ширину овала, не определяя его радиусов, тогда задача построения овала имеет большое множество решений (см. рис. 13.45, а…г).
Применяют также способы построения овалов на основе двух одинаковых опорных кругов, которые соприкасаются (рис. 13.46, а), пересекаются (рис. 13.46, б) или не пересекаются (рис. 13.46, в). При этом фактически задают два параметра: длину овала и один из его радиусов. Эта задача имеет множество решений. Очевидно, что R > ОА
не имеет верхней границы. В частности R = О 1 О 2
(см. рис. 13.46.а, и рис. 13.46.в), а центры О 3
и О 4
определяют, как точки пересечения базовых кругов (см. рис. 13.46,б). Согласно общей теорией точки, сопряжения определяются на прямой, соединяющей центры дуг соприкасающихся окружностей.
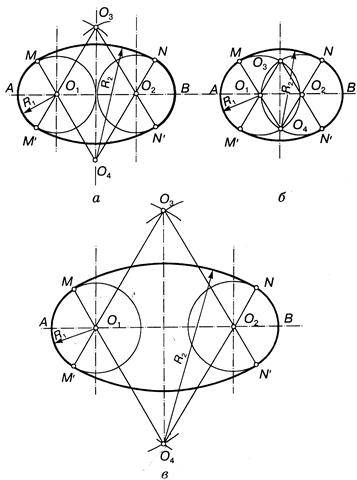
Построение овала с соприкасающимися опорными окружностями
(задача имеет множество решений) (рис. 3.44). Из центров опорных окружностей О
и 0 1
радиусом, равным, например, расстоянию между их центрами, проводят дуги окружностей до пересечения в точках О
2 и О 3 .
Рисунок 3.44
Если из точек О
2 и О 3
провести прямые через центры О
и O 1
, то в пересечении с опорными окружностями получим точки сопряжения С
,
C 1
, D
и D 1
. Из точек О
2 и О 3
как из центров радиусом R 2
проводят дуги сопряжения.
Построение овала с пересекающимися опорными окружностями
(задача также имеет множество решений) (рис. 3.45). Из точек пересечения опорных окружностей С 2
и О 3
проводят прямые, например, через центры О
и O 1
до пересечения с опорными окружностями в точках сопряжения С, С 1 D
и D 1
, а радиусами R 2 ,
равными диаметру опорной окружности,- дуги сопряжения.
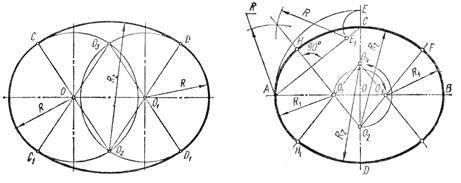
Рисунок 3.45 Рисунок 3.46
Построение овала по двум заданным осям АВ и CD
(рис. 3.46). Ниже приведен один из множества вариантов решения. На вертикальной оси откладываются отрезок ОЕ,
равный половине большой оси АВ.
Из точки С
как из центра проводят дугу радиусом СЕ
до пересечения с отрезком АС
в точке Е 1
. К середине отрезка АЕ 1
восстанавливают перпендикуляр и отмечают точки его пересечения с осями овала O 1
и 0 2 .
Строят точки O 3
и 0 4
, симметричные точкам O 1
и 0 2
относительно осей CD
и АВ.
Точки O 1
и 0 3
будут центрами опорных окружностей радиуса R 1 ,
равного отрезку О 1 А,
а точки O 2
и 0 4 –
центрами дуг сопряжения радиуса R 2 ,
равного отрезку О 2 С.
Прямые, соединяющие центры O 1
и 0 3
с O 2
и 0 4
в пересечении с овалом определят точки сопряжения.
В AutoCAD построение овала производится с помощью двух опорных окружностей одинакового радиуса, которые:
1. имеют точку соприкосновения;
2. пересекаются;
3. не пересекаются.
Рассмотрим первый случай. Строят отрезок OO 1 =2R, параллельный оси Х, на его концах (точки О и О 1) размещают центры двух опорных окружностей радиуса R и центры двух вспомогательных окружностей радиуса R 1 =2R. Из точек пересечения вспомогательных окружностей О 2 и О 3 строят дуги CD и C 1 D 1 соответственно. Удаляют вспомогательные окружности, затем относительно дуг CD и C 1 D 1 обрезают внутренние части опорных окружностей. На рисунке ъъъ полученный овал выделен толстой линией.
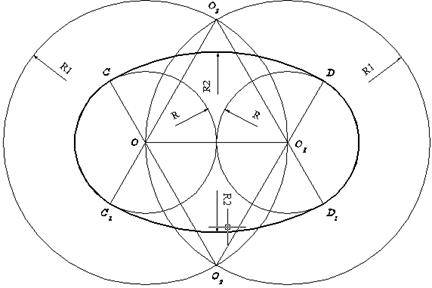
Рисунок Построение овала с соприкасающимися опорными окружностями одинакового радиуса