Сфера и шар — отличия и сходства между геометрическими фигурами

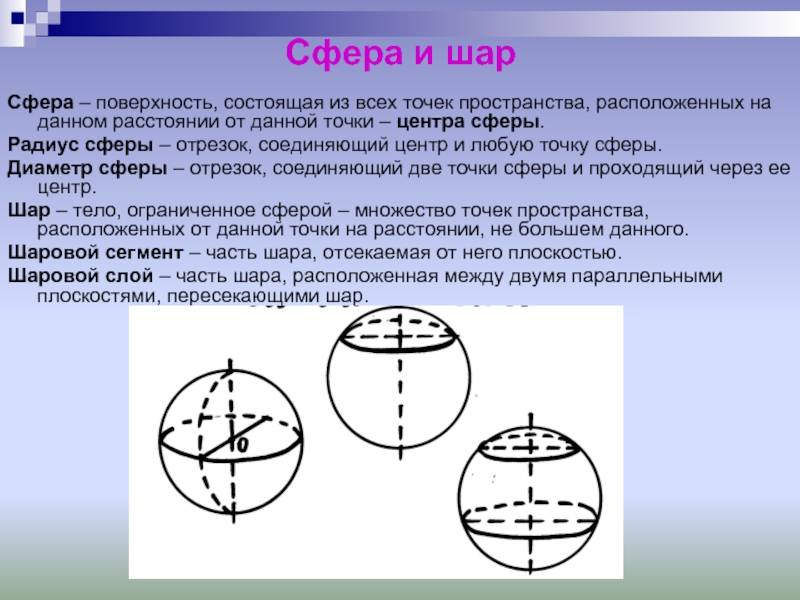
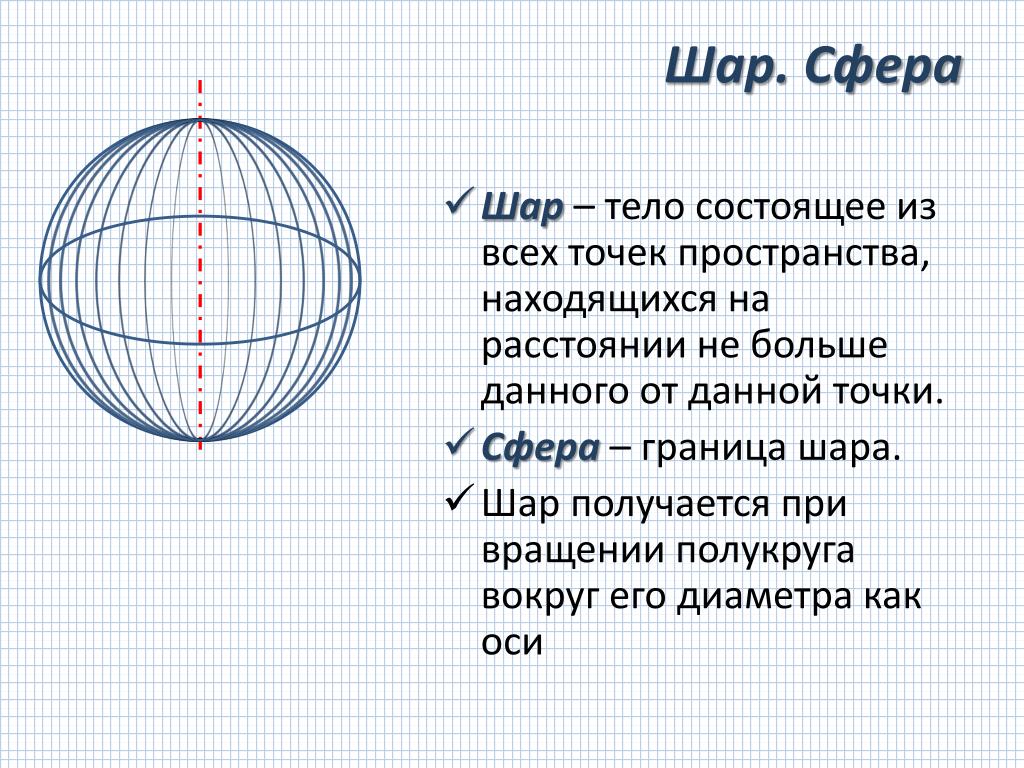
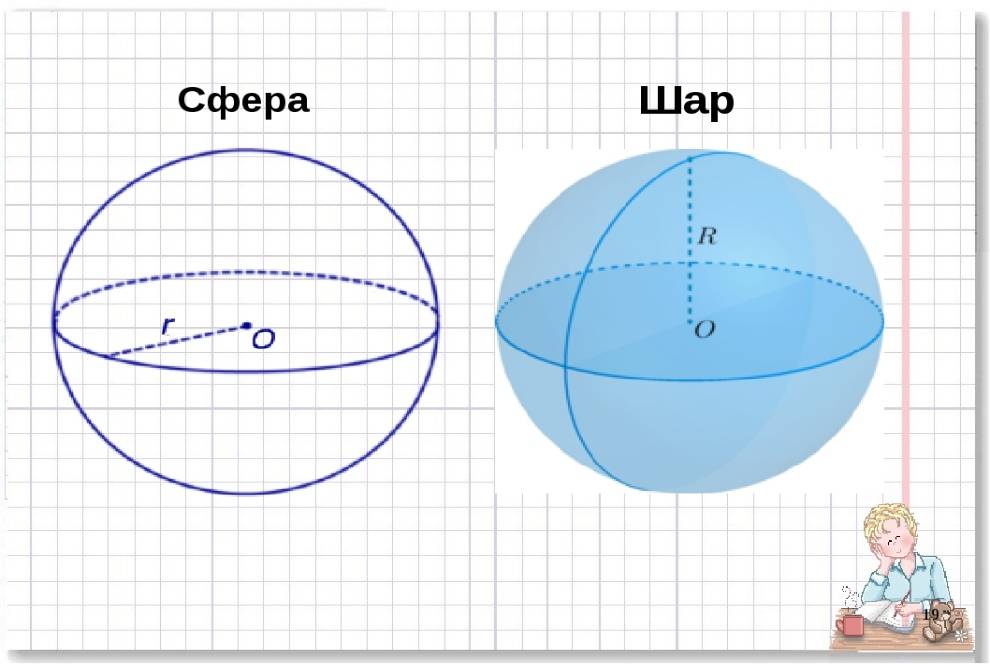
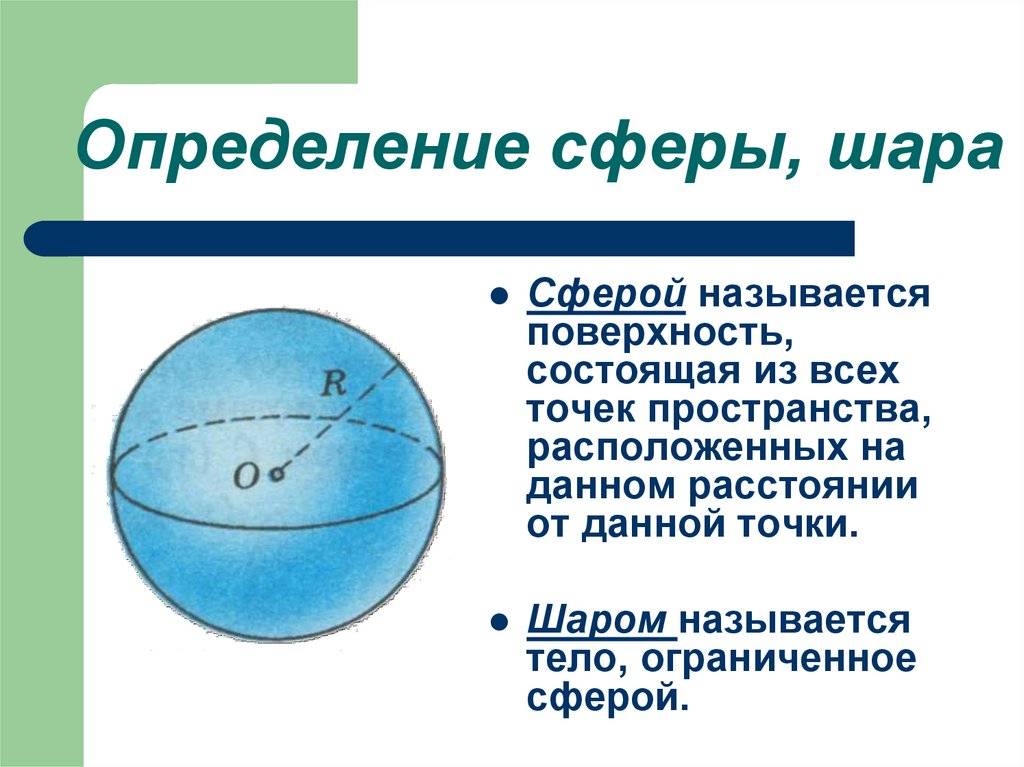
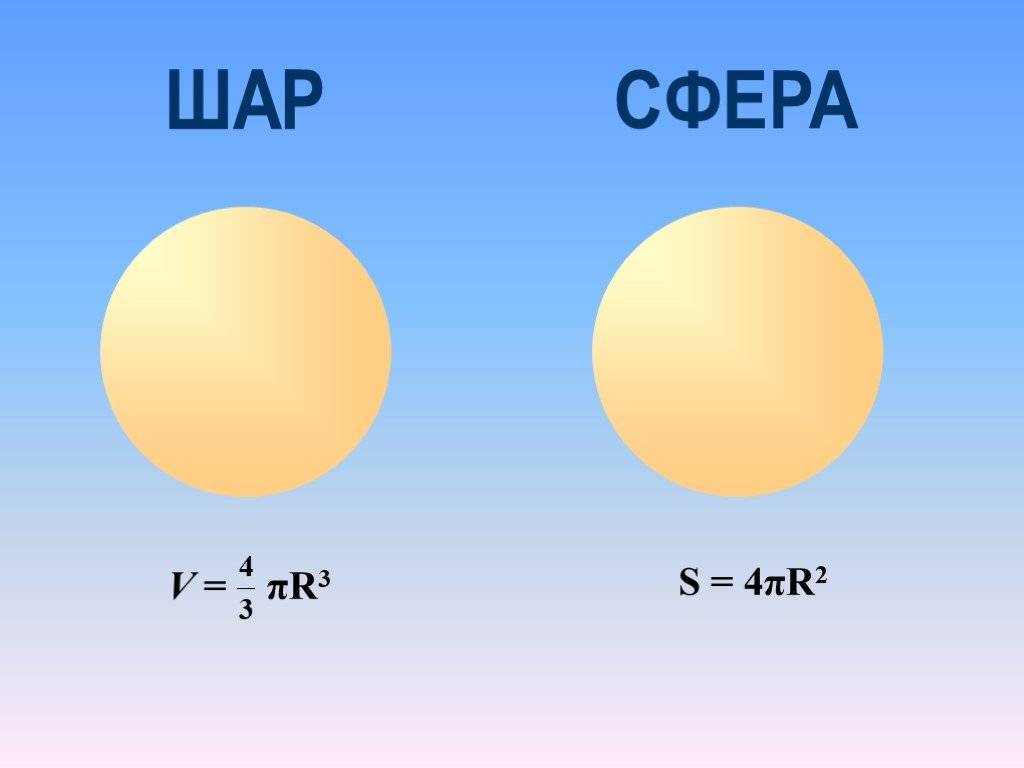
Элементы сферы

Так называются геометрические величины, знание которых позволяет описать либо всю фигуру, либо отдельные ее части. Основными ее элементами являются следующие:

• Радиус r, который уже был упомянут ранее. Он является расстоянием от центра фигуры до сферической поверхности. По сути, это единственная величина, которая описывает все свойства сферы.
• Диаметр d, или D. Это отрезок, концы которого лежат на сферической поверхности, а середина проходит через центральную точку фигуры. Диаметр сферы можно провести бесконечным числом способов, но все полученные отрезки будут иметь одинаковую длину, которая равна удвоенному радиусу, то есть D = 2*R.
• Площадь поверхности S – двумерная характеристика, формула для которой будет приведена ниже.
• Связанные со сферой трехмерные углы измеряются в стерадианах. Один стерадиан – это угол, вершина которого лежит в центре сферы, и который опирается на часть сферической поверхности, имеющей площадь R 2 .

Объем шара

Формула для вычисления объема шара имеет вид:

где R — радиус шара.

Если нужно найти объем шарового сегмента — воспользуйтесь формулой:

V сег =πh 2 (R-h/3), h — высота шарового сегмента.

Площадь поверхности шара или сферы

Чтобы вычислить площадь сферы или площадь поверхности шара (это одно и то же):

где R — радиус сферы.

Архимед очень любил шар и сферу, он даже попросил оставить на его гробницу рисунок, на котором в цилиндр вписан шар. Архимед считал, что объем шара и его поверхность равны двум третьим от объема и поверхности цилиндра, в который вписан шар»

Шар – это тело, состоящее из всех точек пространства, которые находятся на расстоянии, не большем данного от данной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара. Граница шара называется шаровой поверхностью или сферой. Точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, который соединяет центр шара с точкой шаровой поверхности, тоже называется радиусом. Проходящий через центр шара отрезок, который соединяет две точки шаровой поверхности, называется диаметром. Концы любого диаметра называются диаметрально противоположными точками шара.

Шар является телом вращения, так же как конус и цилиндр. Шар получается при вращении полукруга вокруг его диаметра как оси.

Площадь поверхности шара можно найти по формулам:

где r – радиус шара, d – диаметр шара.

Объём шара находится по формуле:

V = 4 / 3 πr 3 ,

где r – радиус шара.

Теорема. Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.

Исходя из данной теоремы, если шар с центром O и радиусом R пересечён плоскостью α, то в сечении получается круг радиуса r с центром K. Радиус сечения шара плоскостью можно найти по формуле

Из формулы видно, что плоскости, равноудалённые от центра, пересекают шар по равным кругам. Радиус сечения тем больше, чем ближе секущая плоскости к центру шара, то есть чем меньше расстояние ОК. Наибольший радиус имеет сечение плоскостью, проходящей через центр шара. Радиус этого круга равен радиусу шара.

Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью, называется большим кругом, а сечение сферы – большим кругом, а сечение сферы – большой окружностью.

Теорема. Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии.

Плоскость, которая и проходит через точку А шаровой поверхности и перпендикулярна радиусу, проведённому в точку А, называется касательной плоскостью. Точка А называется точкой касания.

Теорема. Касательная плоскость имеет с шаром только одну общую точку – точку касания.

Прямая, которая проходит через точку А шаровой поверхности перпендикулярно к радиусу, проведённому в эту точку, называется касательной.

Теорема. Через любую точку шаровой поверхности проходит бесконечно много касательных, причём все они лежат в касательной плоскости шара.

Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Круг ABC – основание шарового сегмента. Отрезок MN перпендикуляра, проведенного из центра N круга ABC до пересечения со сферической поверхностью, – высота шарового сегмента. Точка M – вершина шарового сегмента.

Площадь поверхности шарового сегмента можно вычислить по формуле:

Объём шарового сегмента можно найти по формуле:

V = πh 2 (R – 1/3h),

где R – радиус большого круга, h – высота шарового сегмента.

Шаровой сектор получается из шарового сегмента и конуса, следующим образом. Если шаровой сегмент меньше полушара, то шаровой сегмент дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. Если же сегмент больше полушара, то указанный конус из него удаляется.

Шаровой сектор – это часть шара, ограниченная кривой поверхностью сферического сегмента (на нашем рисунке – это AMCB) и конической поверхностью (на рисунке – это OABC), основанием которой служит основание сегмента (ABC), а вершиной – центр шара O.

Объем шарового сектора находится по формуле:

V = 2/3 πR 2 H.

Шаровый слой – это часть шара, заключённая между двумя параллельными плоскостями (на рисунке плоскостями ABC и DEF), пересекающими сферическую поверхность. Кривая поверхность шарового слоя называется шаровым поясом (зоной). Круги ABC и DEF – основания шарового пояса. Расстояние NK между основаниями шарового пояса – его высота.

сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Шар, сфера и их части

Введем следующие определения, связанные с шаром, сферой и их частями.

Сферой с центром в точке O и радиусомr называют множество точек, расстояние от которых до точки O равно r (рис. 1).

Шаром с центром в точке O и радиусомr называют множество точек, расстояние от которых до точки O не превосходит r (рис. 1).

Рис.1

Таким образом, сфера с центром в точке O и радиусом rявляется поверхностью шара с центром в точке O и радиусом r.

Замечание.Радиусом сферы (радиусом шара) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы (радиусом шара).

Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями (рис. 2).

Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями.

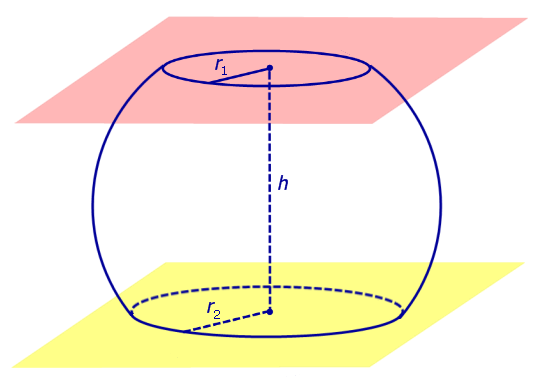
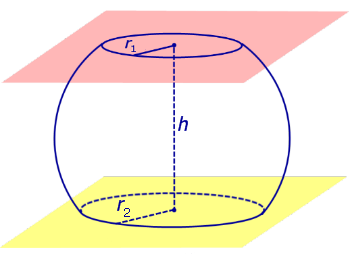
Рис.2

Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.

Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.

Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны между собой. Эти круги называют основаниями шарового слоя.

Высотой шарового слоя называют расстояние между плоскостями оснований шарового слоя.

Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).

Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).

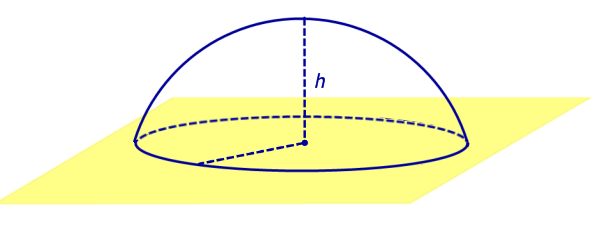
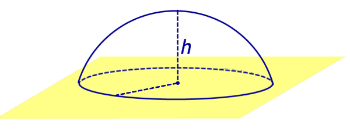
Рис.3

Из определений 3 и 5 следует, что сферический сегмент представляет собой сферический пояс, у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.

Соответственно, шаровой сегмент – это шаровой слой, у которого одна из плоскостей оснований касается шара (рис. 4). Высоту такого шарового слоя называют высотой шарового сегмента.

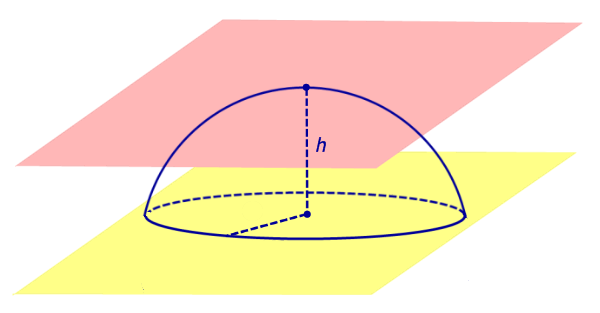
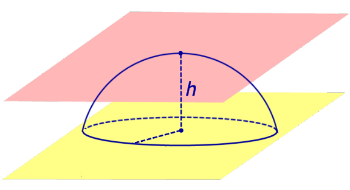
Рис.4

По той же причине всю сферу можно рассматривать как сферический пояс, у которого обе плоскости оснований касаются сферы (рис. 5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).

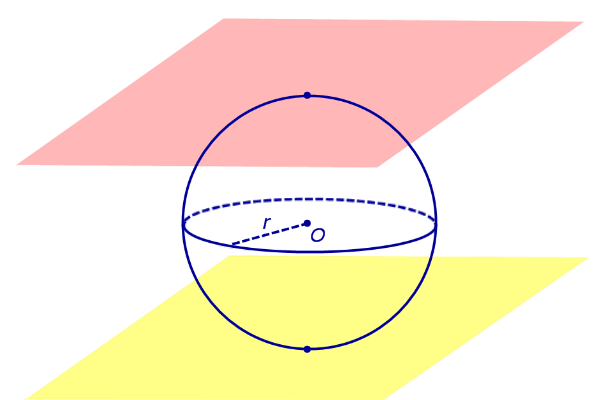
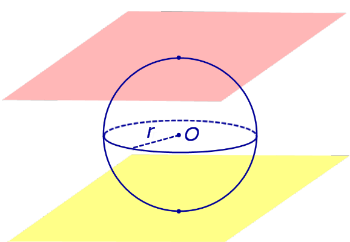
Рис.5

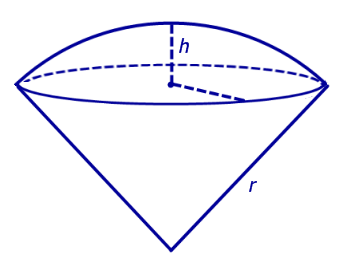
Рис.6

Высотой шарового сектора называют высоту его сферического сегмента.

Замечание.Шаровой сектор состоит из шарового сегмента и конуса с общим основанием. Вершиной конуса является центр сферы.

Применение шара и сферы в жизни

В медицине шар используется, например, в качестве модели для исследования поверхности глазного яблока или формы головного мозга. Также шар используется в физиотерапии для массажа и как спортивный инвентарь для тренировок различных групп мышц.

Сфера, благодаря своей симметричной форме, широко применяется в архитектуре и строительстве. Сферические купола и своды идеально распределяют нагрузку и обеспечивают прочность и устойчивость зданий. Также сферические структуры используются в спортивных сооружениях, например, в футбольных стадионах, чтобы обеспечить оптимальную видимость со всех мест.

Кроме того, шары и сферы находят свое применение в искусстве и дизайне. Их симметричная и эстетически приятная форма делает их популярными объектами для создания скульптур и архитектурных композиций. Также шары и сферы используются в графическом дизайне, в качестве элементов логотипов и маркеров визуального идентификатора компаний или брендов.

Касательная, касательная плоскость к сфере и их свойства

Определение.
Касательная к сфере
– это прямая, которая касается сферы только в одной точке.

Определение.
Касательная плоскость к сфере
– это плоскость, которая соприкасается со сферой только в одной точке.

Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения

Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.

Определение.
Сегмент шара
– это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента
называют круг, который образовался в месте сечения. Высотой сегмента
h
называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.

Формула.
Площадь внешней поверхности сегмента сферы
с высотой h
через радиус сферы R:

S = 2π
Rh

– (греч. sphaira шар). 1) твердое тело, в котором все точки поверхности одинаково отдалены от внутренней точки, называемой центром шар; изображение земли в виде глобуса. 2) часть пространства, в котором планета совершает свой путь. 3) в фигуральном … Словарь иностранных слов русского языка

Жен., греч. шар, шарообразное тело или пустота, или изображенье его на бумаге; в приложении к небесным телам: шар обращаемый на оси своей, представляющий землю нашу, или небесную твердь, с означеньем всех воображаемых кругов. Армилярная сфера,… … Толковый словарь Даля

сфера
– ы, ж. sphère f. <гр. sphaira. 1. геом. Замкнутая поверхность, все точки которой одинаково удалены от одной точки (центра /. БАС 1. | перен. Сфер десять пролетев воздушных, Узрел вдали питейный дом. И. Наумов Ясон. // Ирои комич. поэма 560. 2.… … Исторический словарь галлицизмов русского языка

Сферы, жен. . 1. То же, что шар (мат.). 2. перен. Область, место, пределы, в к рых существует, действует, развивается, применяется что н. (книжн.). «Смотря по свойству поэтического таланта и по степени его выработанности, сфера … Толковый словарь Ушакова

СФЕРА, ы, жен. 1. Область, пределы распространения чего н. С. деятельности. С. влияния. 2. Среда, общественное окружение. В своей сфере. Высшие сферы (о правящих, аристократических кругах). 3. Замкнутая поверхность, все точки к рой равно удалены… … Толковый словарь Ожегова

См. область … Словарь синонимов

Сфера
– (Хабаровск,Россия) Категория отеля: 3 звездочный отель Адрес: Переулок Дежнева 15, Хабаровск … Каталог отелей

Сфера компонент сложных слов, означающих: 1) одну из оболочек планет и звёзд: астеносфера атмосфера барисфера биосфера геосфера гетеросфера гидросфера гомосфера ионосфера литосфера магнитосфера мезосфера стратосфера субстратосфера… … Википедия

– (от греческого sphaira шар), 1) область действия, пределы распространения чего либо (например, сфера влияния). 2) Общественное окружение, среда, обстановка … Современная энциклопедия

– (от греч. sphaira шар) 1) область действия, пределы распространения чего либо (напр., сфера влияния).2) Общественное окружение, среда, обстановка …

Замкнутая поверхность, все точки которой одинаково удалены от одной точки (центра сферы). Отрезок, соединяющий центр сферы с какой либо ее точкой (а также его длина), называется радиусом сферы. Площадь поверхности сферы S=4?R2, где R радиус сферы … Большой Энциклопедический словарь

Книги

• Сфера , Эггерс, Дэйв. Роман лидера новой волны американской литературы, жестокая сатира на современный мир социальных сетей и сплошного белого шума. СФЕРА – корпорация добра: она совершенствует мир, делая его…
• Сфера , Дэйв Эггерс. Мэй Холланд крупно повезло. Она работает в идеальной компании «Сфера» – союз блистательных умов поколения, где все прислушиваются ко всем и все вдохновенно совершенствуют мир. Здесь Мэй…

Шар и сфера — это прежде всего геометрические фигуры, и если шар — это геометрическое тело, то сфера — это поверхность шара. Этими фигурами интересовались еще многие тысячи лет назад до н.э.

Впоследствии когда было открыто, что Земля — это шар, а небо — небесная сфера, получило развитие новое увлекательное направление в геометрии — геометрия на сфере или сферическая геометрия. Для того, чтобы рассуждать о размере и объеме шара, нужно сначала дать ему определение.

Площадь сферы

Замечание 2

Площадь сферы вычисляется по формуле:

$S = 4πR^2$.

Для вычисления площади сферы нужно ознакомиться с понятием степени числа, зная определение которой формулу площади сферы можно переписать в следующем виде:

$S = 4πR^2= 4πR \cdot R$.

Пример 3

Вычислить площадь сферы, если её радиус равен $2 \frac{4}{5}$ см.

Решение.

Воспользуемся формулой площади сферы:

$S = 4πR^2$.

Подставим значение радиуса в формулу и, используя преобразование дробей и правила умножения дробей, найдем результат:

$S=4πR^2=4 \cdot 3,14 \cdot (2 \frac{4}{5})^2=4 \cdot 3,14 \cdot (\frac{14}{5})^2=4 \cdot 3,14 \cdot \frac{196}{25}=\frac{4 \cdot 3,14 \cdot 196}{25}=\frac{2461,76}{25}≈98,47 \ см^2$.

Ответ: $S≈98,47 \ см^2$.

Понятие сферы и шара

Если оглядеться вокруг, то можно найти множество шарообразных и сферических объектов в окружающем мире. Такая форма характерна для космических тел, в том числе, нашей планеты. С мячами разнообразных размеров, фактур и цветов люди встречаются во время занятий спортом и на игровых соревнованиях. Многие фрукты и овощи обладают круглой формой. Подобные примеры касаются реальной жизни. В рамках курса стереометрии перечисленные понятия отличаются

Важно уметь разбираться в терминологии и отличать фигуры друг от друга по ряду характерных признаков

Сферой называют поверхность, в состав которой входит совокупность точек, равноудаленных от какой-то одной центральной точки, называемой центром.

Шар представляет собой материальное тело, в состав которого включены все точки в пространственном измерении, расстояние от которых до определенной центральной точки не более чем заданная величина.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

При рассмотрении вышеуказанных понятий часто встречается определение радиуса. Под ним подразумевают прямую, ограниченную парой точек, одна из которых лежит на сфере, а вторая — представляет собой центр этой фигуры. Кроме того, аналогичный отрезок играет роль радиуса шара, помещенного во внутреннее пространство анализируемой сферической фигуры. Наглядно представить эти понятия несложно, если обратиться к изображению, расположенному ниже на рисунке:

Другое важное понятие касается диаметра сферы. Такое название присуще отрезку, пересекающему центральную точку сферической фигуры

При этом начало и конец данной линии расположены на рассматриваемой сфере. Непосредственно сфера является фрагментом шара. Существует аналогичное утверждение, когда окружность признают частью круга. Исходя из расшифровки термина сферы, можно сформулировать справедливое заключение о равенстве радиусов этой фигуры.

Таким образом, центральная точка сферической фигуры делит диаметр пополам. В свою очередь, диаметр сферы в два раза превышает размер радиуса аналогичного объекта. Кроме того, сфера представляет собой тело вращения. Из данного определения можно сделать вывод о способе получения сферической фигуры. Достаточно лишь повернуть половину окружности относительно ее диаметра, чтобы образовалась сфера.

Что такое сфера?

Сфера схожа с шаром, но есть некоторые различия. Форма сферы очень похожа на форму шара, но у нее нет реальных границ или поверхности. Поэтому, сфера можно представить как бесконечное число точек, которые находятся на одинаковом равном расстоянии от центра.

Диаметр сферы — это прямая, проходящая через центр сферы и имеющая концы на ее поверхности. Диаметр является длиной отрезка, соединяющего любые две точки на поверхности сферы.

Сфера обладает такими свойствами, как равноудаленность всех точек от центра и симметричность относительно центра. Эти особенности делают сферу важным геометрическим объектом в различных областях науки, техники и естественных наук.

Объем сферы можно вычислить по формуле V = (4/3) * π * r^3, где r — радиус сферы. Радиус — это расстояние от центра сферы до ее поверхности.

Определение сферы в геометрии

Сфера имеет одну поверхность, которая полностью закрыта и не имеет ребер или углов. Ее поверхность является абсолютно гладкой и однородной.

Центр сферы — это точка в пространстве, которая находится на равном удалении от всех точек ее поверхности. Из центра сферы к любой точке ее поверхности можно провести линию, которая называется радиусом сферы.

Сфера также имеет другую важную характеристику — диаметр. Диаметр сферы — это отрезок, соединяющий две точки ее поверхности и проходящий через центр сферы. Диаметр является наибольшей возможной длиной, которую можно измерить на поверхности сферы.

Одно из основных свойств сферы — ее объем. Объем сферы — это количество пространства, занимаемое ею. Его можно вычислить по формуле: V = (4πR^3)/3, где V — объем сферы, а R — ее радиус.

Сферы часто встречаются в ежедневной жизни и используются в различных областях, таких как физика, математика, архитектура и многие другие. Знание характеристик и свойств сферы позволяет производить точные измерения и анализы в реальном мире.

Характеристики сферы	Описание
Поверхность	Гладкая, закрытая, не имеет ребер и углов
Центр	Точка, находящаяся на равном удалении от всех точек поверхности сферы
Диаметр	Отрезок, соединяющий две точки поверхности сферы и проходящий через ее центр
Объем	Количество пространства, занимаемого сферой

Примеры использования сферы в повседневной жизни

Сферы широко используются в нашей повседневной жизни:

1. В медицине: врачи используют сферические линзы в очках для коррекции зрения. Они могут иметь положительную или отрицательную силу, что позволяет корректировать гиперметропию или короткозорость.
2. В архитектуре: сферические купола используются в строительстве, например, в крыше Пантеона в Риме. Купол образует полусферу и поддерживается на круглых колоннах, создавая величественный и просторный интерьер.
3. В научных исследованиях: сферы используются в различных экспериментах и моделировании. Например, в физике сферические модели применяются для изучения гравитационного взаимодействия и расчета объемов и плотностей различных объектов.
4. В сфере развлечений: шары используются в играх, как например, футбольный мяч или бильярдный шар. Они позволяют участникам игры контролировать и направлять движение шара с помощью ударов или бросков.
5. В промышленности: сферы используются в различных технических приборах и механизмах. Например, шариковые подшипники обеспечивают плавное и эффективное движение механизмов.

Сферы, благодаря своей форме и свойствам, нашли широкое применение в различных сферах нашей жизни. Они позволяют нам решать задачи, связанные с объемом, поверхностью и расстояниями. Диаметр и объем сферы являются основными характеристиками, которые определяют ее свойства и функциональность.

Симметрия: шар и сфера

Шар и сфера имеют одинаковую симметрию, что делает их похожими структурами. Оба объекта могут быть описаны как окружность, вращающаяся вокруг своей оси. Этот тип симметрии называется осевой симметрией, так как объекты имеют ось вращения, вокруг которой они симметричны.

Осевая симметрия шара и сферы проявляется в том, что любая плоскость, проходящая через их центр, разделяет их на две половины, симметричные по форме и размеру. Если разбить шар или сферу на две половины, получится точно идентичное отражение одной половины в другой. Эта осевая симметрия делает шар и сферу привлекательными объектами для исследования и рассмотрения.

Однако, помимо осевой симметрии, у сферы есть и еще одна особенность — сферическая симметрия. Сферическая симметрия означает, что сфера выглядит одинаково, независимо от того, с какой стороны на нее смотреть. У шара эта симметрия не наблюдается, так как он является двумерным объектом и имеет только одну плоскость симметрии.

Иными словами, шар имеет только одну плоскость симметрии, в то время как сфера имеет бесконечное количество плоскостей симметрии. Эта особенность делает сферу более симметричной и гармоничной по своему устройству, чем шар.

В итоге, хотя шар и сфера имеют общую осевую симметрию, сфера обладает дополнительной сферической симметрией, делая ее еще более симметричной в своей форме и структуре. Это придает сфере особую красоту и привлекательность, что делает ее одним из наиболее изучаемых и ценных объектов в геометрии и физике.

Небольшое погружение в один из разделов математики

Для начала потребуется вспомнить о существовании науки геоме́трии (в несколько вольном переводе с греческого это слово означает «землемеренье») — обособленном разделе математики, специализирующемся на изучении пространственных структур, их отношений между собой и различных возникающих из этого обобщений

Важно, что несмотря на подобное «приземлённое» происхождения названия эта наука оперирует сугубо абстрактными понятиями, которые в привычном нам мире не существуют в прямом физическом воплощении

Одно из таких базовых понятий — это геометрическая точка. Напрягите своё воображение: в отличие от «точки карандашом», «точки от булавки» и так далее эта точка представляет из себя полностью абстрактный объект в воображаемом пространстве без каких-либо измеримых характеристик типа «толщины», «цвета» и так далее (математики любят при этом произносить словосочетание «нульмерный объект»). В принципе, всё остальное в геометрии будет далее определяться исходя именно из этой абстракции.

Следующее нужно для дальнейших рассуждений понятие — это «ритуальная» математическая фраза «геометри́ческое ме́сто то́чек» (ГМТ). C её помощью описывается некоторое множество (совокупность) точек, подпадающих под определённое отношение (свойство) — таким образом задаётся «геометрическая фигура». Пример: сфе́ра (от древнегреческого σφαῖρα, изначально обозначающего мяч/шар) — это геометрическое место таких точек пространства, которое можно описать как равноудалённое (находящееся на строго одном расстоянии) от некоторой заданной точки, обычно называемой «центром сферы».

Сфера

Расстояние же от центра сферы до этого ГМТ принято называть «радиусом сферы»

Во время всех этих манипуляций важно продолжать помнить, что сфера — понятие более эфемерное, чем даже всем привычный и знакомый мыльный пузырь: у любого мыльного пузыря всё-таки есть вполне ощутимая стенка из водно-мыльной плёнки микроскопической толщины, которую можно физически измерить (и даже проткнуть), а у сферы — нет!

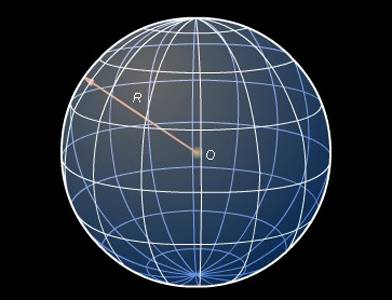
Сфера и радиус сферы

Теперь обратимся к определению шара: под шаром понимается совокупность всех таких точек пространства, что находится от определённой точки (центра шара) на расстоянии, не большем заданного (радиуса шара). Иначе говоря, шар является «геометрическим телом» — тем, что согласно первичному определению Евклида «имеет длину, ширину и глубину» (в современных учебниках это определение менее наглядно: «часть пространства, ограниченная своей образуемой формой»).

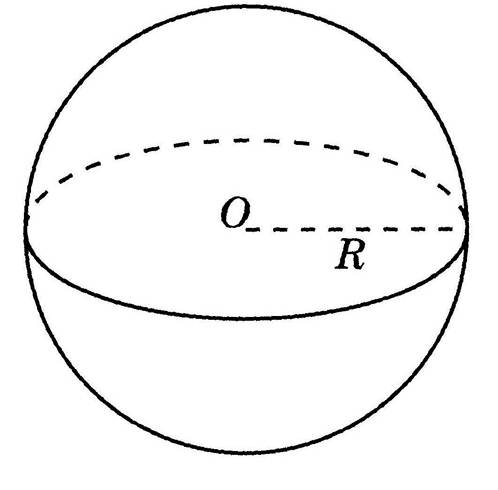
Шар

Попутно отметим, что использованные здесь способы задания сферы и шара через центр и радиус — не единственные: например, задание сферы/шара в пространстве можно выполнить посредством вращения окружности, круга и т.д. (глубоко заинтересовавшимся этим вопросом настоятельно рекомендуется ознакомиться с отдельным разделом геометрии под названием «Фигуры и тела вращения», поскольку это часто применяемый способ задания самых различных геометрических фигур и тел в пространстве).

Таким образом, и в случае сферы, и в случае шара приходится иметь дело с определённым образом заданным геометрическим местом точек (то есть геометрической фигурой), однако лишь в случае шара можно говорить о геометрическом теле. Любопытно отметить, что строго говоря сферу из шара можно «вычесть»: в этом случае математики говорят об «открытом шаре». Однако «по умолчанию» имеет место «замкнутый шар», где сфера является его естественной границей и принадлежащей ему частью.

Сравнение Иисуса Христоса и антихриста с шаром и сферой

Аналогично геометрическим определениям, Иисус Христос и антихрист, как символы добра и зла, имеют свои особенности и воздействие на людей.

1. Иисус Христос — божественная энергия:

• Иисус Христос называется «светом мира» и «спасителем». Его энергия олицетворяет добро, любовь и милосердие.
• Аналогично шару, Иисус Христос является центром света, вокруг которого собираются истинные верующие.
• Иисус Христос объединяет людей своей энергией и дарует им надежду и веру в более справедливое будущее.

Антихрист — злая энергия:

• Антихрист символизирует зло, иллюзию и раздоры. Его цель — отвратить людей от пути истины и подстроить под себя религиозные и мировые системы.
• Похоже на сферу, антихрист находится вне центра света и воздействует на людей извне.
• Антихрист разделяет и порабощает людей своей энергией и привносит разрушение в церковь и общество.

• Иисус Христос — как шар, объединяет людей своей божественной энергией.
• Антихрист — как сфера, воздействует на людей своей злой силой извне.

Веруют ли вы в присутствие Иисуса Христоса и антихриста — решать только вам

Однако важно помнить, что наша вера и добрые поступки могут ослабить энергию зла и укрепить связь с божественной энергией

Какие площади и объемы имеют шар и его части?

Площадь поверхности шара можно рассчитать по формуле S=4πR^2, где R — радиус шара. Объем шара вычисляется по формуле V=(4/3)πR^3. Части шара, такие как полусфера или сектор шара, имеют свои собственные формулы для расчета площади и объема.