Чем отличается тетраэдр от пирамиды

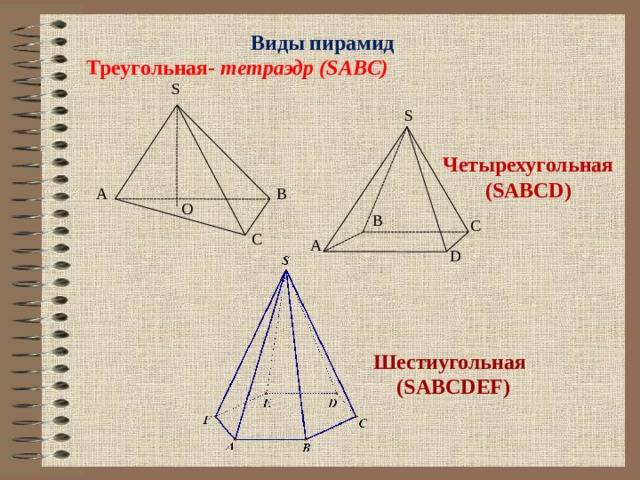
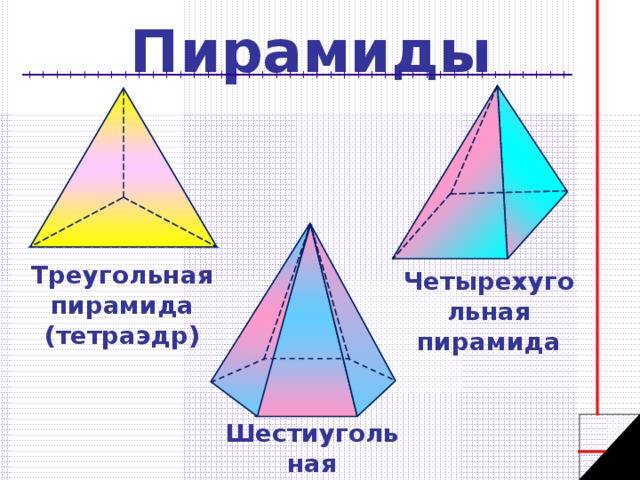
Свойства пирамиды

Пирамида с равным боковыми ребрами

Все углы между боковыми ребрами и основанием пирамиды равны.

Свойство 2

Вокруг основания пирамиды можно описать окружность, центр которой будет совпадать с проекцией вершины на ее основание.

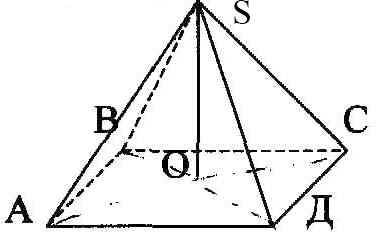
Точка F– проекция вершины E на основание ABCD; одновременно является центром этого основания.
R– радиус описанной окружности.

Боковые грани пирамиды наклонены к основанию под одинаковым углом

Примечание: для перечисленных выше свойств верны и обратные формулировки. Например, для Свойства 1: если все углы между боковыми ребрами и плоскостью основания пирамиды равны, значит эти ребра имеют одинаковую длину.

Свойства треугольной пирамиды

Количество граней: треугольная пирамида имеет четыре грани — одну треугольную базу и три треугольные боковые грани.
Количество ребер: у треугольной пирамиды есть шесть ребер — три ребра, образующих боковые грани, и три ребра, образующих контуры базы.
Количество вершин: в треугольной пирамиде четыре вершины — три вершины боковых граней и одна вершина в центре базы.
Углы: в треугольной пирамиде существуют различные углы, такие как углы между боковыми гранями и углы между боковыми гранями и базой. Углы могут быть равными или различными в зависимости от формы и размеров пирамиды.
Объем: объем треугольной пирамиды может быть вычислен по формуле V = (A * h) / 3, где A — площадь треугольника базы, а h — высота пирамиды.
Площадь поверхности: площадь поверхности треугольной пирамиды может быть вычислена по формуле S = A + (a * p) / 2, где A — площадь треугольника базы, a — длина одного ребра боковой грани, а p — полупериметр треугольника базы.

Треугольная пирамида является интересной и уникальной геометрической фигурой, обладающей указанными свойствами. Ее структура и форма делают ее полезной в различных областях, от архитектуры до математики.

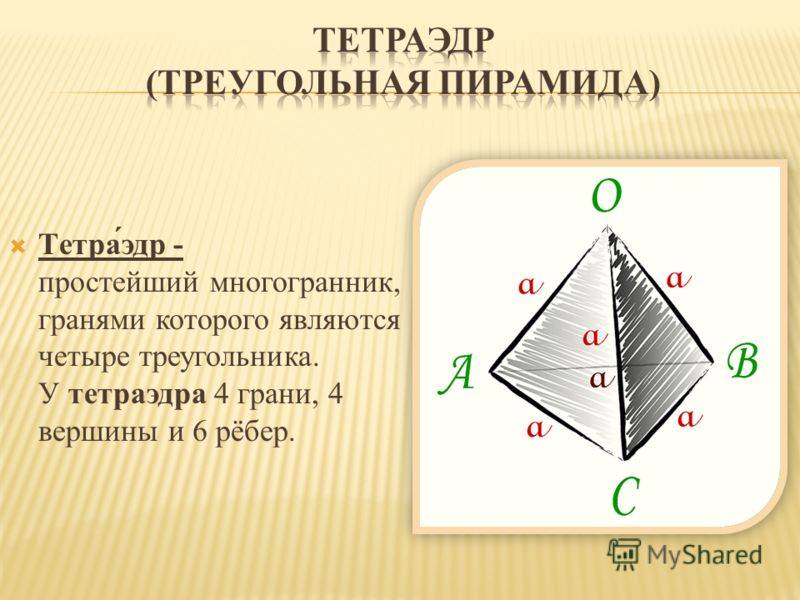
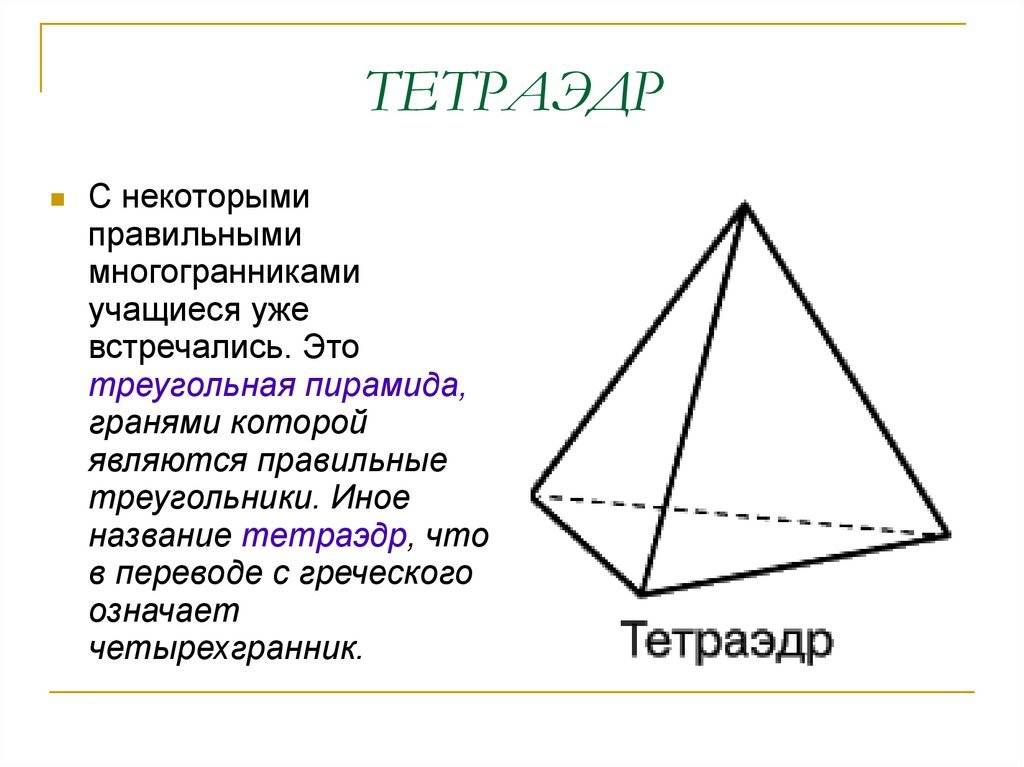
Структура и свойства тетраэдра

Основные свойства тетраэдра:

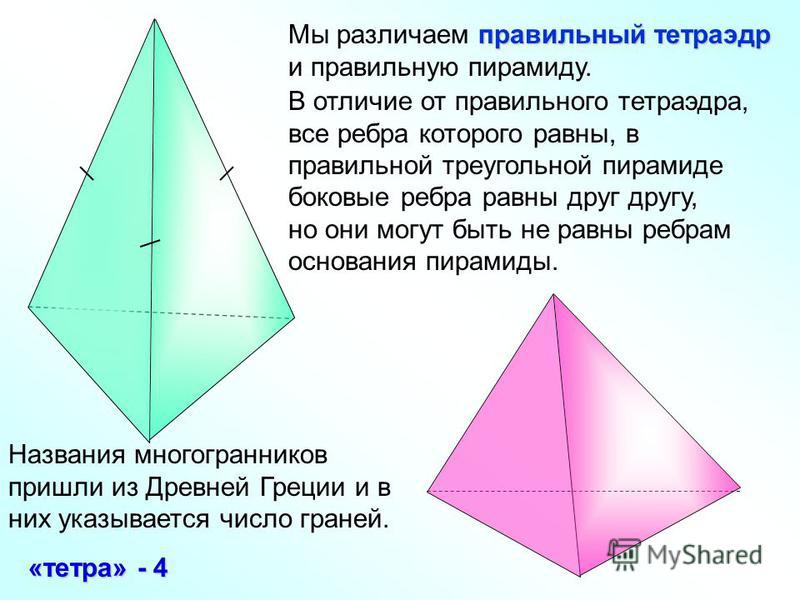
Тетраэдр является правильным, если все его грани равны и все углы между плоскостями граней равными. В противном случае, тетраэдр называется неправильным.
Тетраэдр является выпуклым телом, что означает, что он не имеет вогнутых участков.
Все ребра тетраэдра равны между собой, а все плоскости граней пересекаются в одной общей точке, которая называется вершиной тетраэдра.
У каждой вершины тетраэдра три ребра, и они образуют равносторонний треугольник.
Угол между любыми двумя гранями тетраэдра составляет 60 градусов.

Тетраэдр является одним из самых простых и наиболее известных полиэдров. Из-за своей кристаллической формы, тетраэдр широко используется в науке, инженерии и архитектуре.

Параллелепипед

Призма, в основании которой лежит параллелограмм, называется параллелепипедом.

У параллелепипеда все грани – параллелограммы.

Грани параллелепипеда, не имеющие общих вершин, называются противолежащими.

У параллелепипеда противолежащие грани параллельны и равны.

Диагональю параллелепипеда, как и многогранника вообще, называется отрезок, соединяющий вершины параллелепипеда, не лежащие в одной его грани.

Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.

Точка пересечения диагоналей параллелепипеда является его центром симметрии.

Прямоугольным параллелепипедом называется такой прямой параллелепипед, в основании которого лежит прямоугольник.

Все грани прямоугольного параллелепипеда являются прямоугольниками.

Длины рёбер прямоугольного параллелепипеда, выходящих из одной вершины, называются его измерениями или линейными размерами.

У прямоугольного параллелепипеда три измерения.

В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трёх его измерений:

В прямоугольном параллелепипеде верно:

В прямоугольном параллелепипеде, как и во всяком параллелепипеде, есть центр симметрии – точка пересечения его диагоналей. У него есть также три плоскости симметрии, проходящие через центр симметрии параллельно парам противолежащих граней. На первом рисунке, приведённом выше, показана одна из таких плоскостей. Она проходит через середины четырех параллельных ребер параллелепипеда.

Если у параллелепипеда все линейные размеры разные, то у него нет других плоскостей симметрии, кроме трёх названных.

Если же у параллелепипеда два линейных размера равны, то есть он является правильной четырёхугольной призмой, то у него есть еще две плоскости симметрии. Это плоскости диагональных сечений, показанные на втором рисунке.

Прямоугольный параллелепипед, у которого все три измерения равны, называется кубом.

Диагональ куба в квадратный корень из трёх раз больше его стороны:

для площади полной поверхности:

Четыре сечения куба являются правильными шестиугольниками (одно из них показано на рисунке) – эти сечения проходят через центр куба перпендикулярно четырём его диагоналям.

У куба девять плоскостей симметрии:

три из них, проходя через середины четырёх параллельных ребер куба, дают в сечениях квадраты;
остальные шесть – это все плоскости диагональных сечений куба.

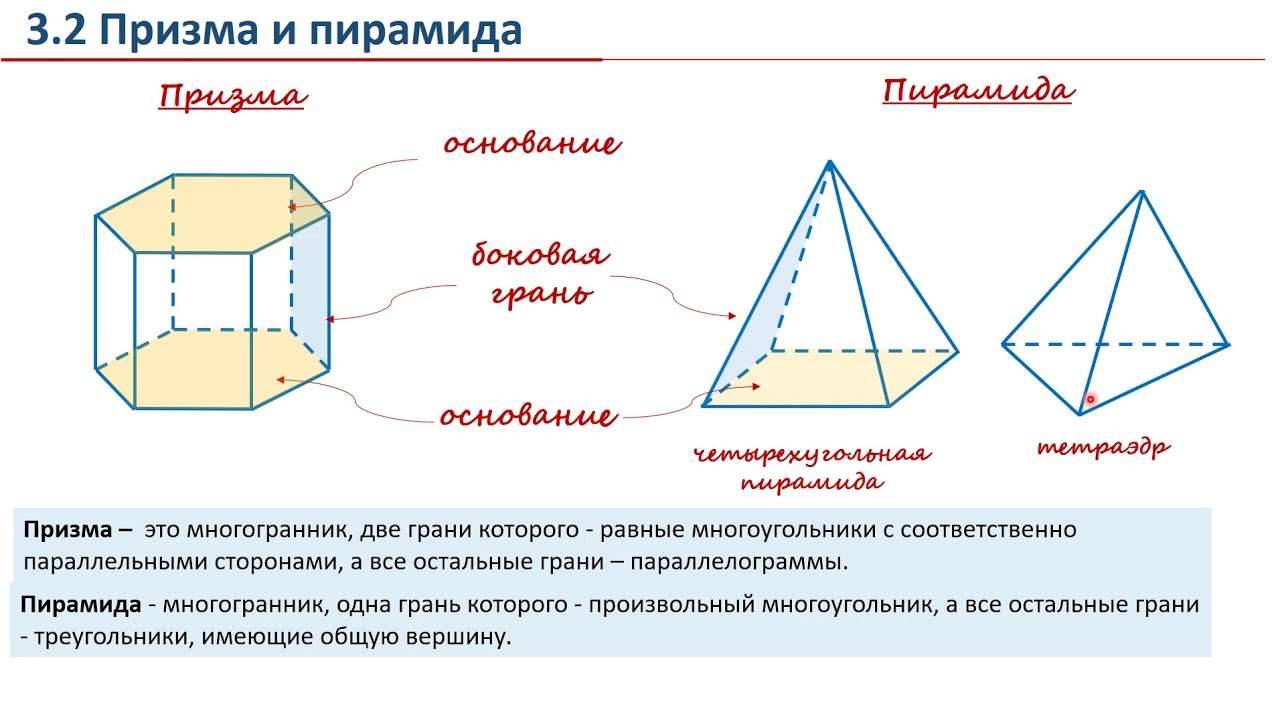
Пирамида

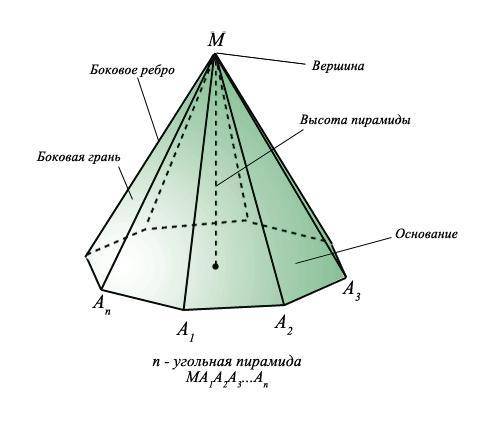
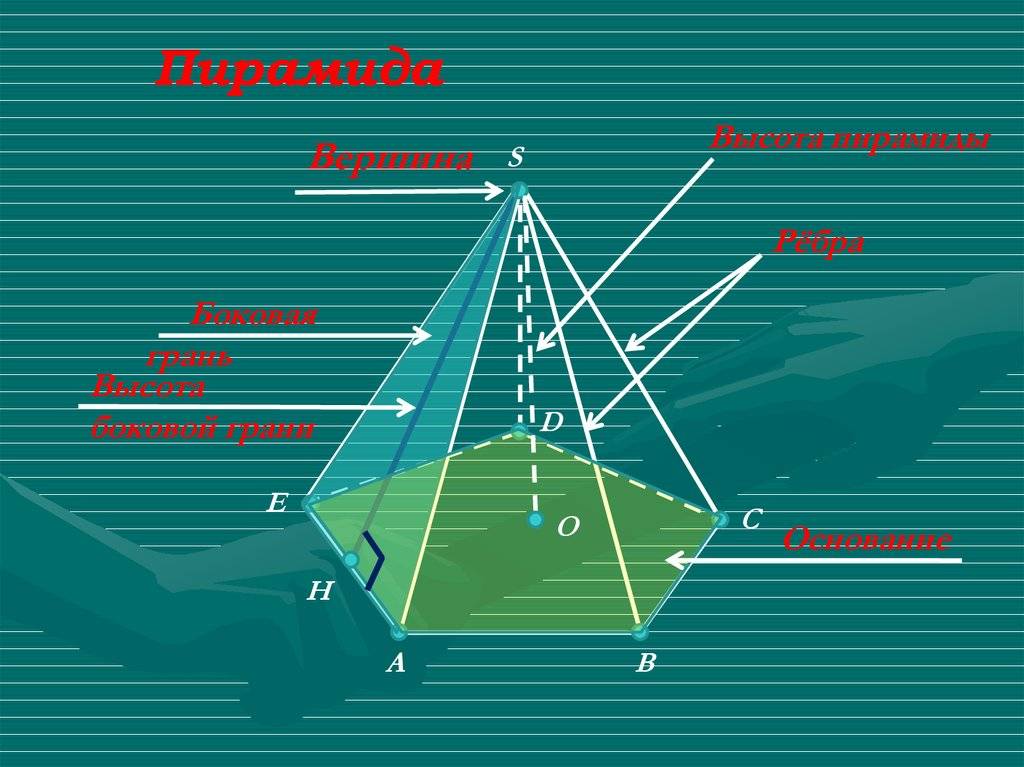
Пирамидой (например, SABCDE ) называется многогранник, который состоит из плоского многоугольника (пятиугольник ABCDE ) – основания пирамиды, точки ( S ), не лежащей в плоскости основания,– вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания.

Отрезки ( SA , SB , SC , SD , SE ), соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами.

Поверхность пирамиды состоит из основания (пятиугольник ABCDE ) и боковых граней. Каждая боковая грань – треугольник. Одной из его вершин является вершина пирамиды, а противолежащей стороной – сторона основания пирамиды:

ΔSAB , ΔSBC , ΔSCD , ΔSDE , ΔSEA – боковые грани.

Боковой поверхностью пирамиды называется сумма площадей ее боковых граней.

Высотой пирамиды ( SО ) называется перпендикуляр, проведённый из вершины пирамиды к плоскости основания.

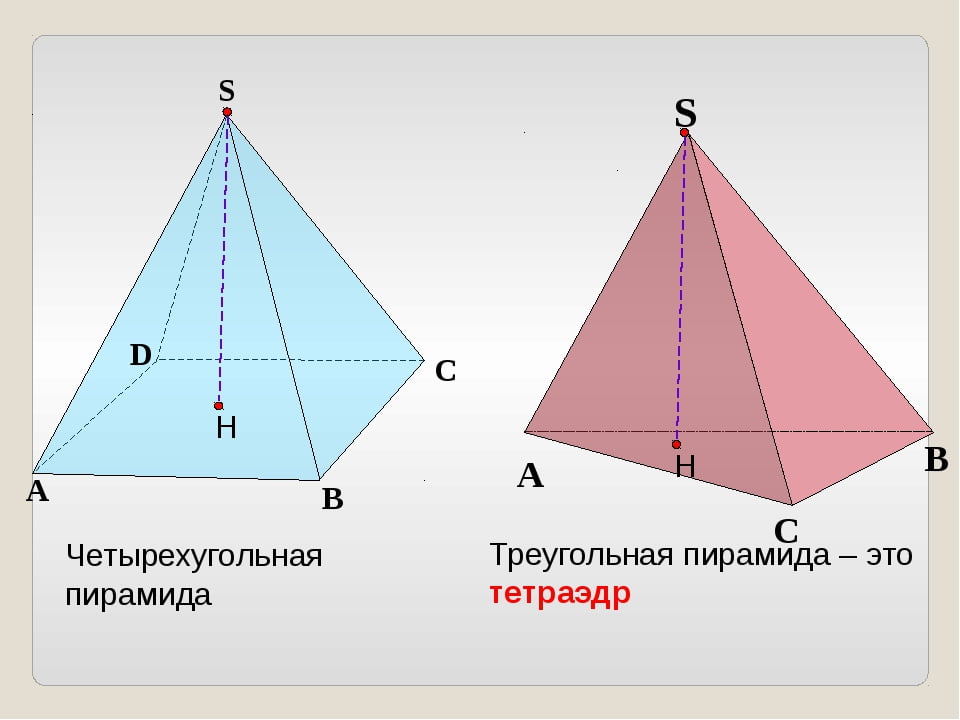
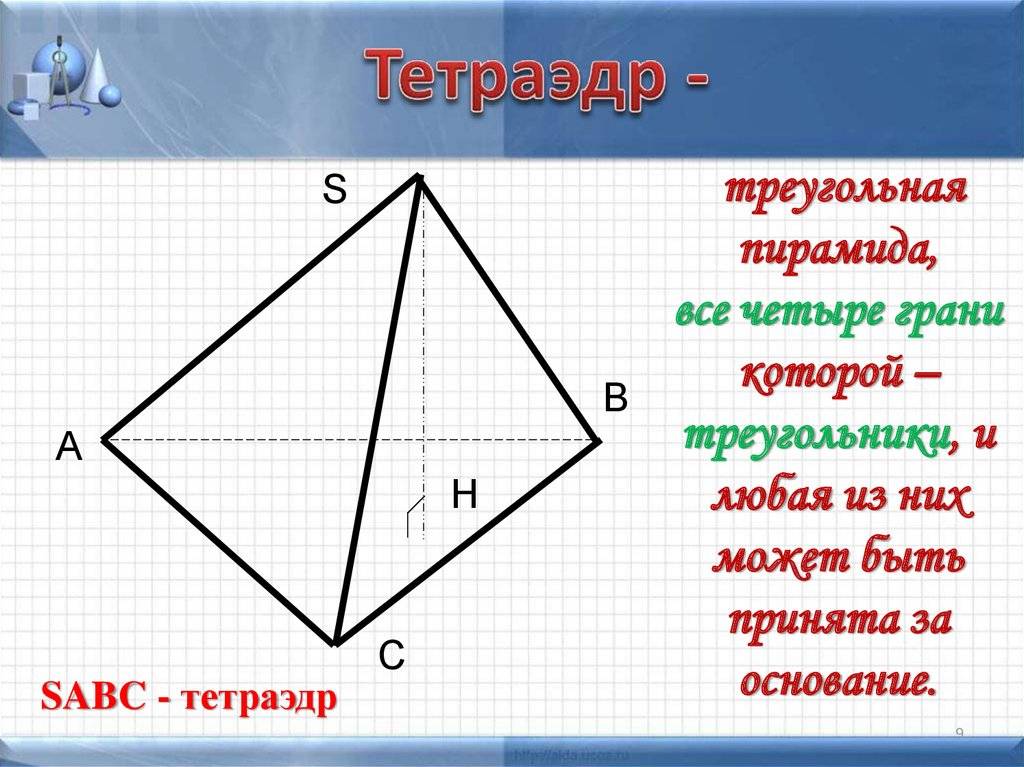
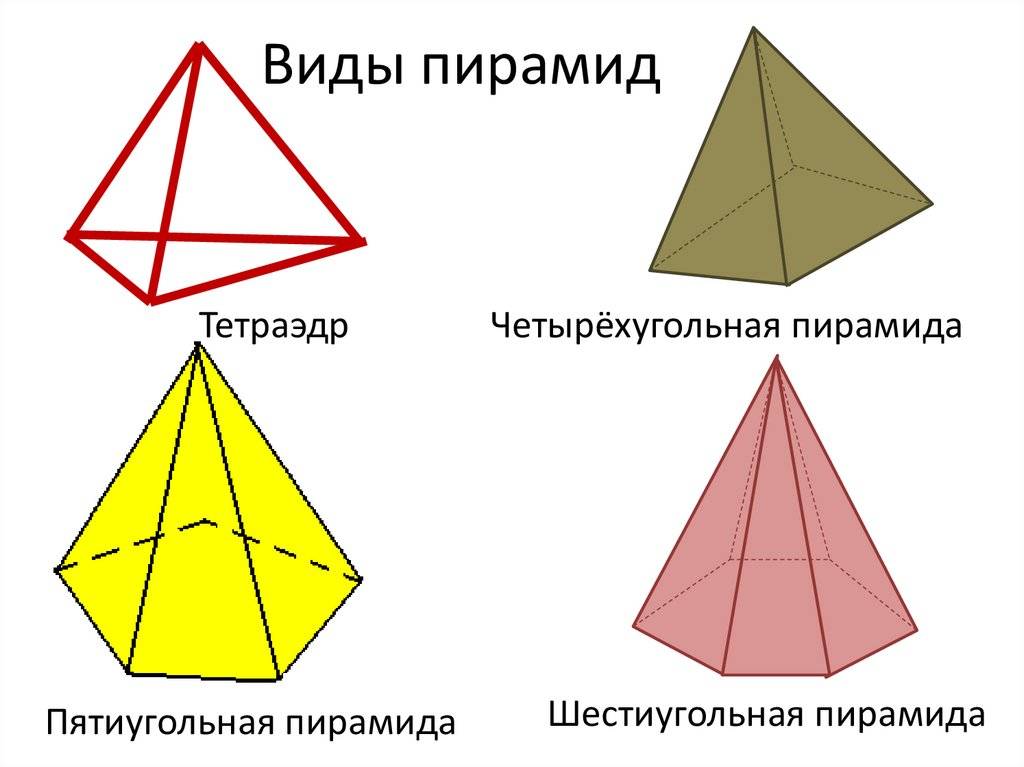
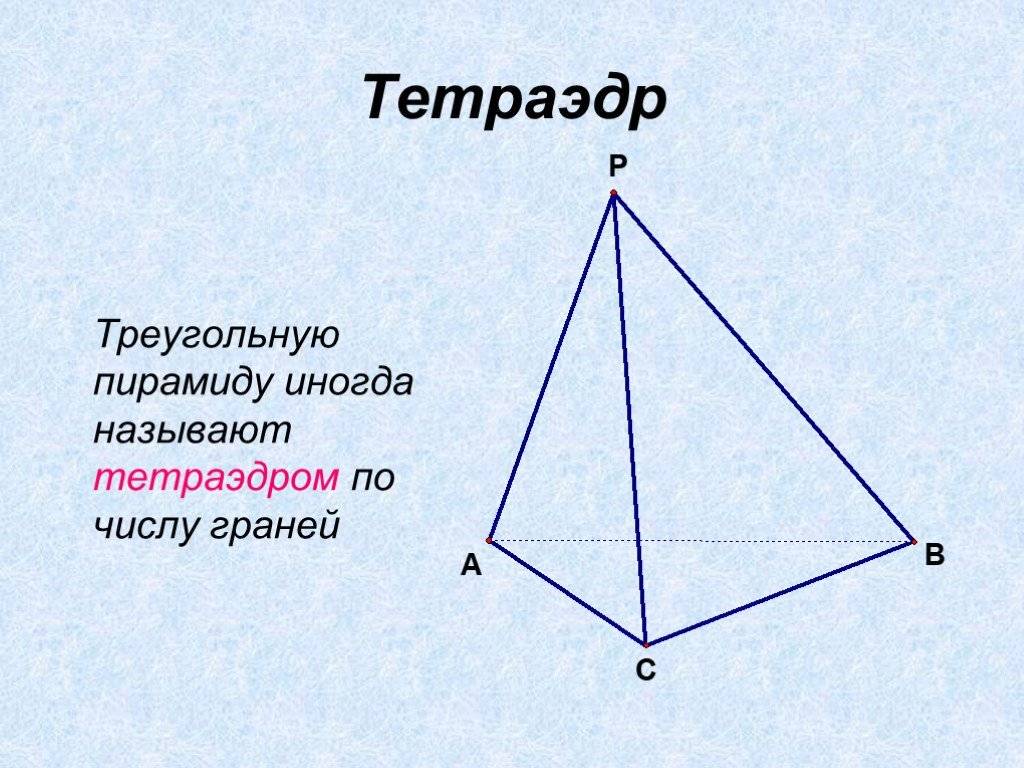
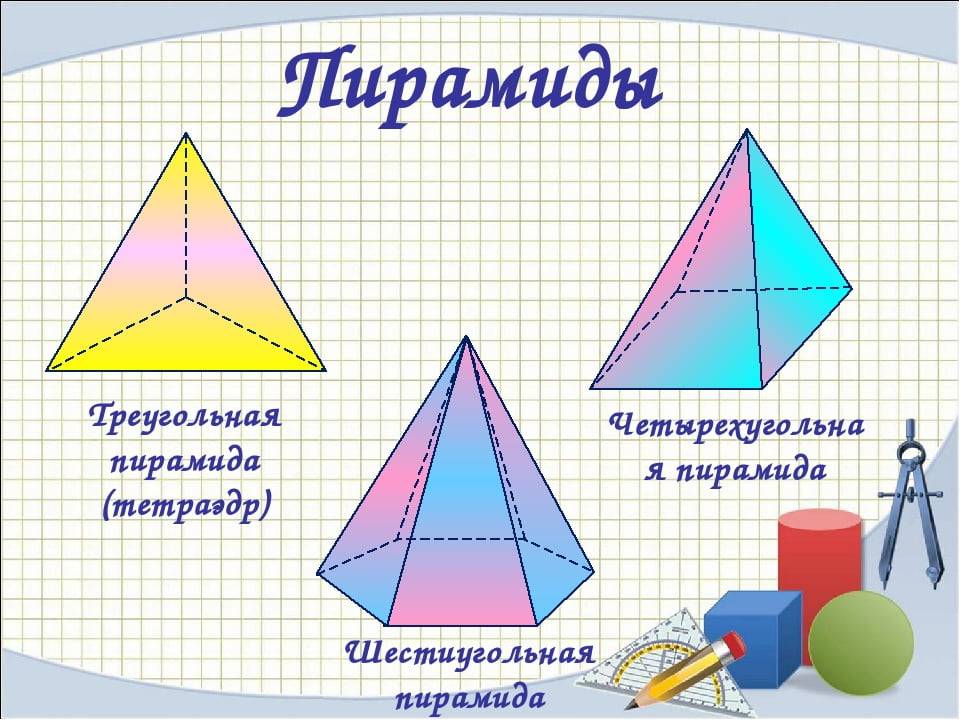
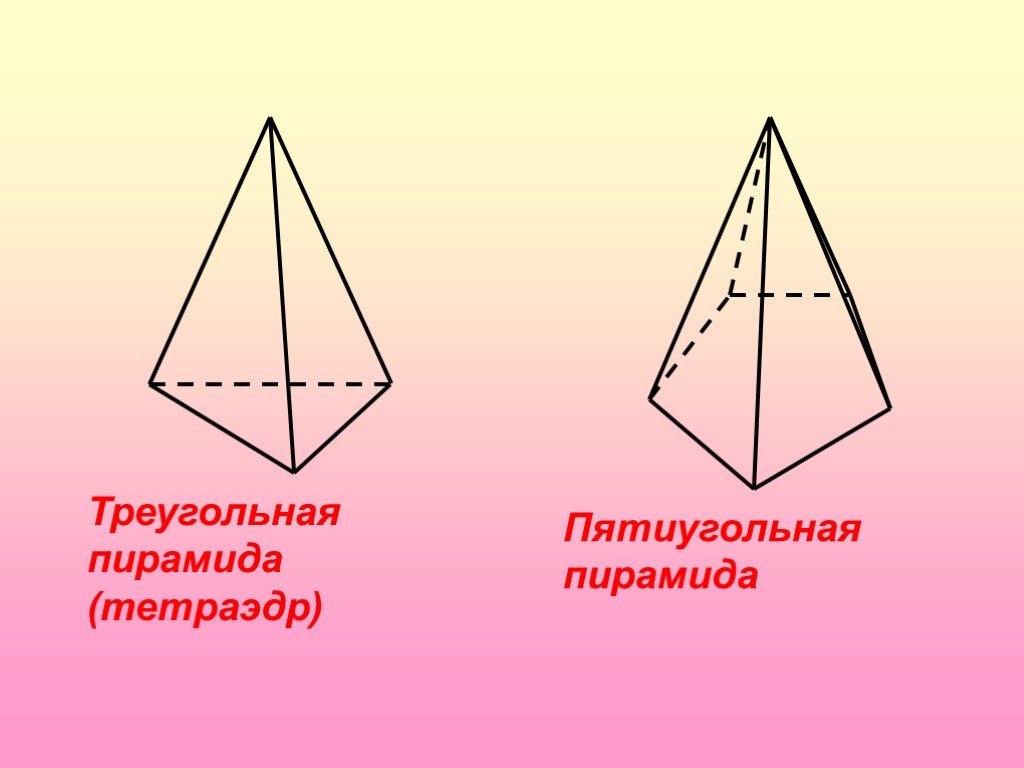
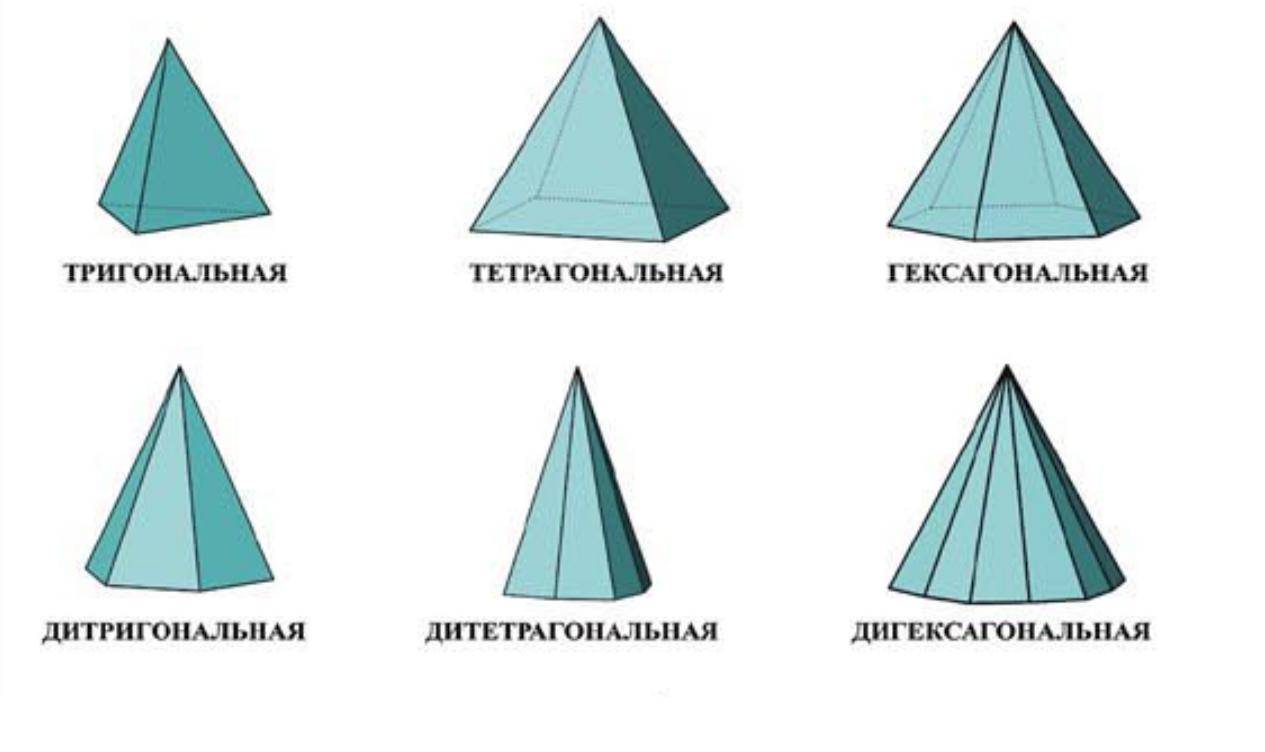
Пирамида называется n -угольной, если ее основанием является n -угольник. Треугольная пирамида называется также тетраэдром.

α – угол наклона бокового ребра SA пирамиды к плоскости её основания;

β – угол наклона боковой грани ( SED ) пирамиды к плоскости её основания.

Основание высоты пирамиды является центром окружности, описанной около основания пирамиды, тогда и только тогда, когда выполняется одно из условий:

все боковые ребра равны;
боковые ребра образуют с плоскостью основания равные углы;
боковые ребра образуют равные углы с высотой пирамиды.

Основание высоты пирамиды является центром окружности, вписанной в основание пирамиды, тогда и только тогда, когда выполняется одно из условий:

боковые грани наклонены к плоскости основания под одним углом;
высоты боковых граней равны;
боковые грани образуют равные углы с высотой пирамиды.

Объём пирамиды равен трети произведения площади основания на высоту пирамиды:

Площадь полной поверхности любой пирамиды равна сумме площадей боковой поверхности и основания:

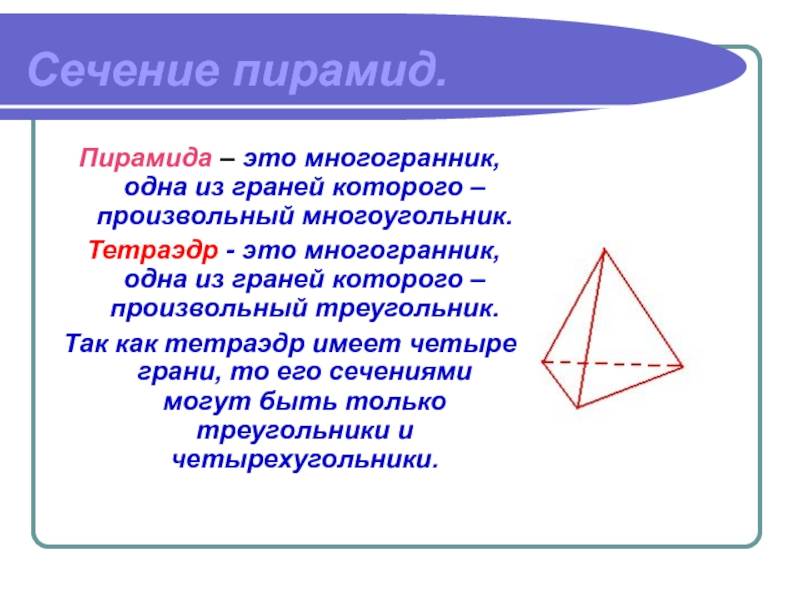
Сечения пирамиды плоскостями, проходящими через ее вершину, представляют собой треугольники. В частности, треугольниками являются диагональные сечения. Это сечения плоскостями, проходящими через два несоседних боковых ребра пирамиды.

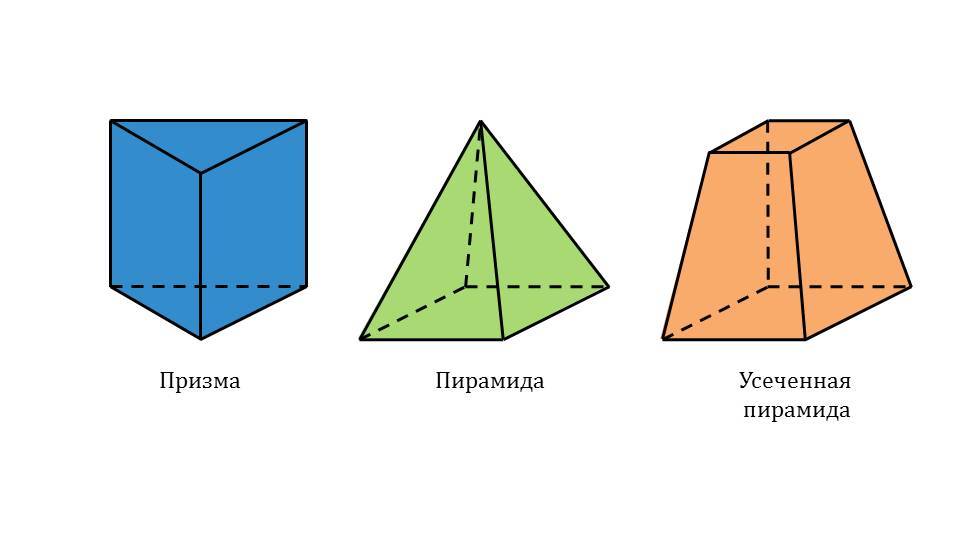
Плоскость, которая пересекает пирамиду и параллельна её основанию, делит её на две части:

многогранник, называемый усеченной пирамидой ( AВСA₁В₁С₁ ).

Грани усеченной пирамиды, лежащие в параллельных плоскостях ( ΔАВС и ΔA₁В₁С₁ ), называются основаниями, остальные грани ( АA₁В₁В , АA₁С₁С , ВВ₁С₁С ) называются боковыми гранями.

Основания усеченной пирамиды представляют собой подобные многоугольники, боковые грани – трапеции.

Высота усеченной пирамиды ( ОО₁ ) – это расстояние между плоскостями её оснований.

Если S₁ и S₂ – площади оснований усечённой пирамиды и h – её высота, то для объёма усеченной пирамиды верно:

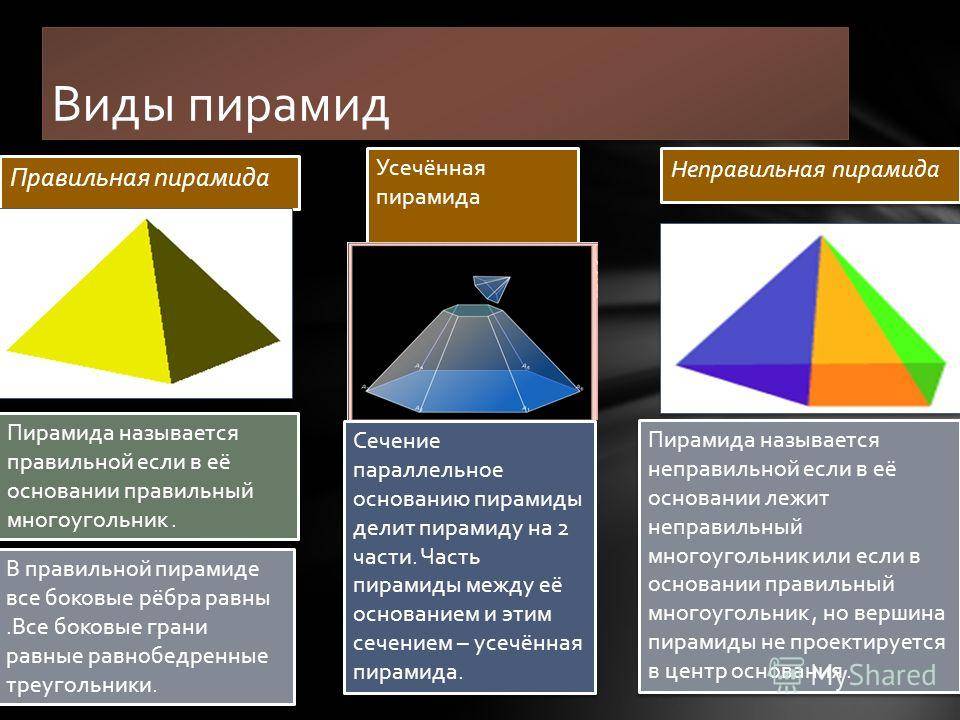
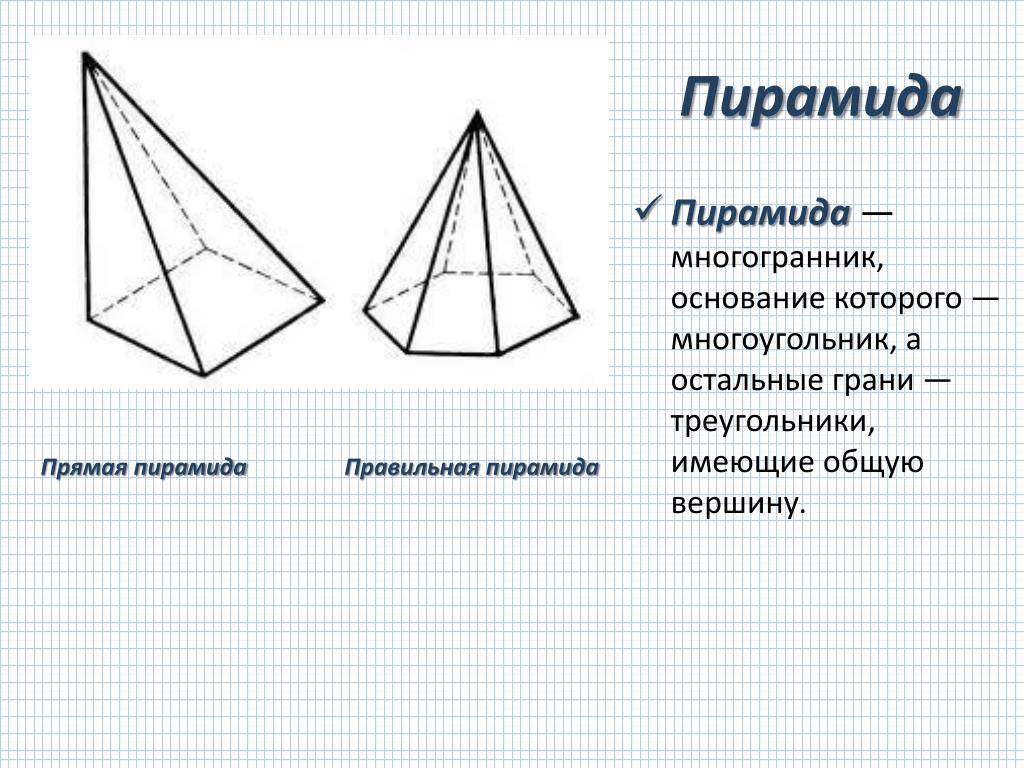
Пирамида (например, SABCD ) называется правильной, если ее основанием является правильный многоугольник ( ABCD – квадрат ), а основание высоты совпадает с центром этого многоугольника ( О – центр описанной и вписанной окружностей основания).

Осью правильной пирамиды называется прямая, содержащая ее высоту.

Боковые ребра правильной пирамиды равны.

Боковые грани правильной пирамиды – равные равнобедренные треугольники.

Высота боковой грани правильной пирамиды ( SL ), проведенная из ее вершины к стороне основания, называется апофемой.

Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему:

Усеченная пирамида (например, АВСDA₁В₁С₁D₁ ), которая получается из правильной пирамиды, также называется правильной.

Боковые грани правильной усеченной пирамиды ( АA₁В₁В , АA₁С₁С , DD₁С₁С , АA₁D₁D ) – равные равнобокие трапеции; их высоты называются апофемами.

Примечание

↑ Погорелов А.В. Геометрия: 10-11 классы. — М.: Просвещение, 2014. — 175 с.
↑ Киселёв А.П. Геометрия / Под ред.Глаголева Н.А.. — М.: ФИЗМАТЛИТ, 2004. — 328 с.
Начала Евклида. Книги XI-XV / пер. с греч. Д.Д.Мордухай-Болтовского. — М.—Л.: Гос.изд-во технико-теоретической литературы, 1950. — 334 с.
История математики с древнейших времён до начала XIX столетия. Т.1 / под ред. А.П.Юшкевича. — М.: Наука, 1970. — 353 с.
Математический энциклопедический словарь / Под ред. Прохорова Ю.В.. — М.: Советская энциклопедия, 1988. — 847 с.
↑ Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия. — М.: Просвещение, 2013. — 255 с.
Математическая энциклопедия. Т.4 / Под ред. Виноградова И.М.. — М.: Советская энциклопедия, 1983. — 608 с.
. Дата обращения: 30 июля 2023.

Определение

Пирамида – это геометрическая фигура в пространстве; многогранник, который состоит из основания и боковых граней (с общей вершиной), количество которых зависит от количества углов основания.

Для рисунка выше:

Основание (четырехугольник ABCD)– грань фигуры, являющая многогранником. Ей не принадлежит вершина.
Вершина пирамиды (точка E)– общая точка всех боковых граней.
Боковые грани– треугольники, которые сходятся в вершине. В нашем случае это: AEB, AED, BEC и CED.
Боковые ребра– стороны боковых граней, за исключением тех, которые принадлежат основанию. Т.е. это AE, BE, CE и DE.
Высота пирамиды (EF или h) – перпендикуляр, опущенный из вершины пирамиды на ее основание.
Высота боковой грани (EM)– высота треугольника, являющегося боковой гранью фигуры. В правильной пирамиде называются апофемой.
Площадь поверхности пирамиды– площадь основания и всех ее боковых граней.
Развёртка пирамиды– фигура, полученная при “разрезе” пирамиды, т.е. при совмещении всех ее граней в плоскости одной из них. Для правильной четырехугольной пирамиды развертка в плоскости основания выглядит следующим образом.

Основные понятия

Некоторые пространственные фигуры, изучаемые в стереометрии, называют телами или геометрическими телами. Наглядно тело надо представлять себе как часть пространства, занятую физическим телом и ограниченную поверхностью.

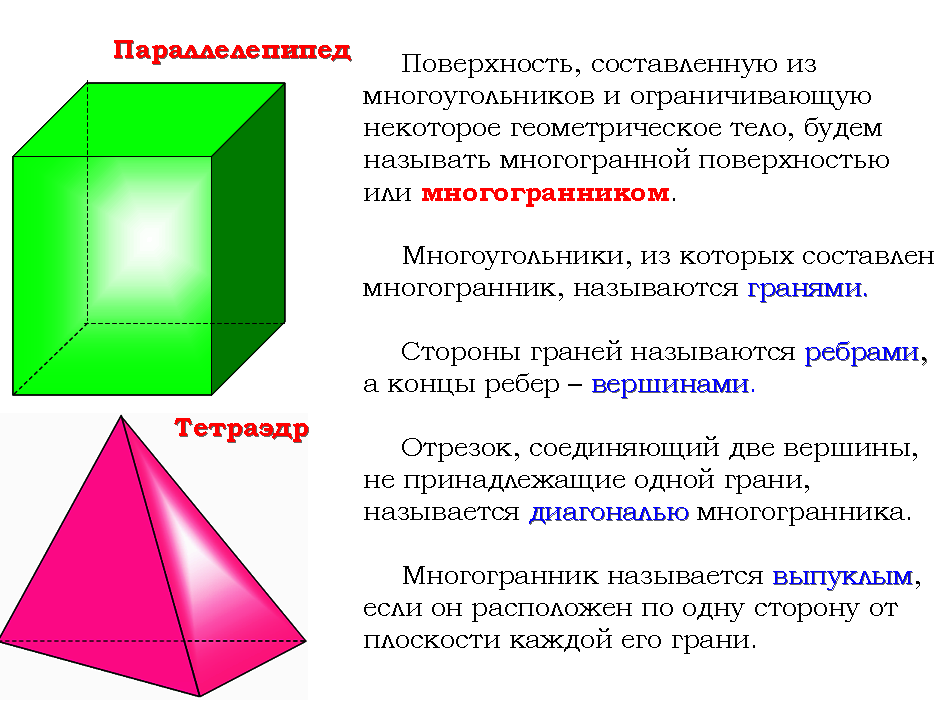
Многогранником называется геометрическое тело, поверхность которого состоит из конечного числа плоских многоугольников.

Выпуклым называется многогранник, если он расположен по одну сторону плоскости, проведённой через любой многоугольник, образующий поверхность данного многогранника.

Многоугольники, составляющие поверхность многогранника, называются его гранями; стороны многоугольников – рёбрами; вершины – вершинами многогранника:

ABC , DEF , ABED , BCFE , ACFD – грани;

AB , BC , AC , DE , EF , DF , AD , BE , CF – рёбра;

A , B , C , D , E , F – вершины многогранника ABCDEF .

Теорема Эйлера для многогранников:

Если V — число вершин выпуклого многогранника, R — число его ребер и G — число граней, то верно равенство:

Что определяет форму тела?

Форма тела определяется его геометрией, то есть взаимным расположением и формой его граней, ребер и вершин. Геометрические параметры тела, такие как длины, углы и радиусы, определяют его форму и свойства.

Основным геометрическим параметром тела является количество его граней, ребер и вершин. Например, у тетраэдра есть четыре грани, шесть ребер и четыре вершины, в то время как у треугольной пирамиды есть три грани, шесть ребер и четыре вершины.

Другой важным параметром являются углы между гранями и ребрами тела. У тетраэдра все углы равны 60 градусам, а у треугольной пирамиды углы между гранями обычно различны.

Размеры граней, ребер и вершин также влияют на форму тела. Например, если длины всех ребер тела одинаковы, то оно будет иметь симметричную форму, в отличие от тела с различными длинами ребер.

Также важно учесть, что форму тела может определять не только его геометрия, но и его внутренняя структура и особенности материала, из которого оно состоит

Форму тела определяет его геометрия: взаимное расположение и форма граней, ребер и вершин.
Геометрические параметры, такие как количество граней, ребер и вершин, а также углы и размеры граней и ребер, определяют форму тела.
Форма тела может зависеть не только от его геометрии, но и от внутренней структуры и материала.

Практическое применение

Архитектура:

В архитектуре треугольные пирамиды могут использоваться в качестве крыш или куполов в различных сооружениях. Благодаря своей устойчивой форме треугольные пирамиды обладают хорошей несущей способностью и могут выдерживать большие веса. Тетраэдры, благодаря своей компактности, могут применяться для создания устойчивых и прочных конструкций.

Химия и физика:

Тетраэдры широко используются в химии и физике для представления молекул. Так, например, четыре атома водорода могут образовать тетраэдральную структуру в молекуле метана (CH4). Треугольные пирамиды также могут использоваться в химии, например, для представления структуры молекулы аммиака (NH3).

Математика:

Тетраэдры и треугольные пирамиды играют важную роль в математике. Они используются в геометрии для изучения форм и объемов, а также для решения различных проблем и задач. Одна из важных концепций, связанных с тетраэдром, — это понятие пирамидального угла, которое находит свое применение в геометрии и тригонометрии.

Игры и головоломки:

Тетраэдры и треугольные пирамиды могут использоваться в играх и головоломках. Кубик Рубика, например, состоит из нескольких треугольных пирамид, которые собираются в кубическую форму. Тетраэдры также могут быть использованы для создания различных головоломок и пазлов.

Как видно из приведенных примеров, тетраэдр и треугольная пирамида имеют широкое практическое применение и находят свое применение в различных областях, от архитектуры до науки и игр.