В чем разница между радиусом и диаметром?

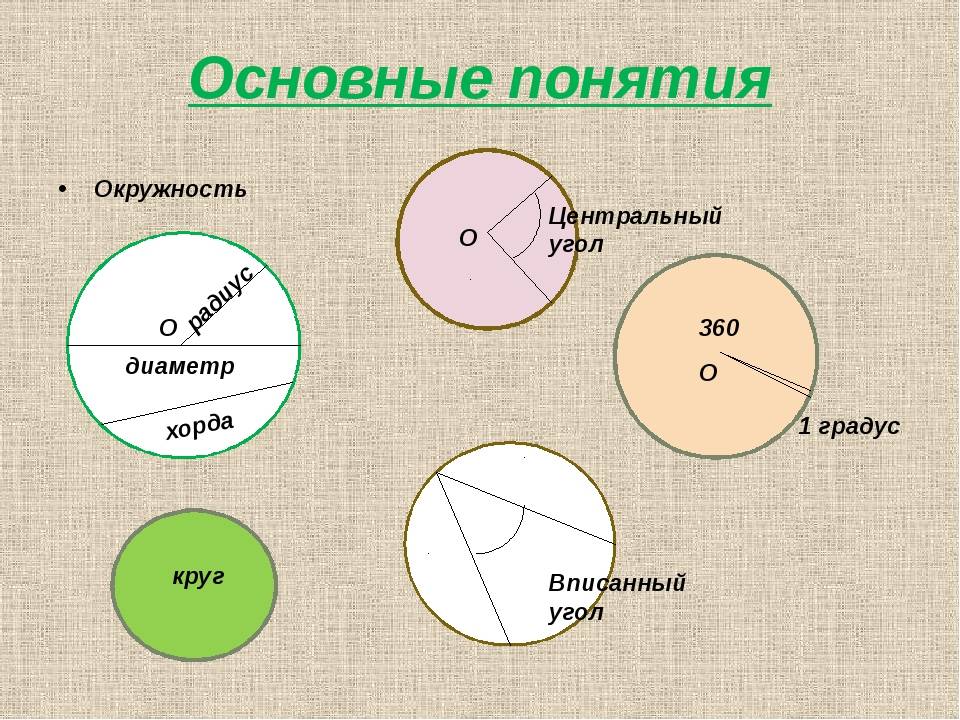
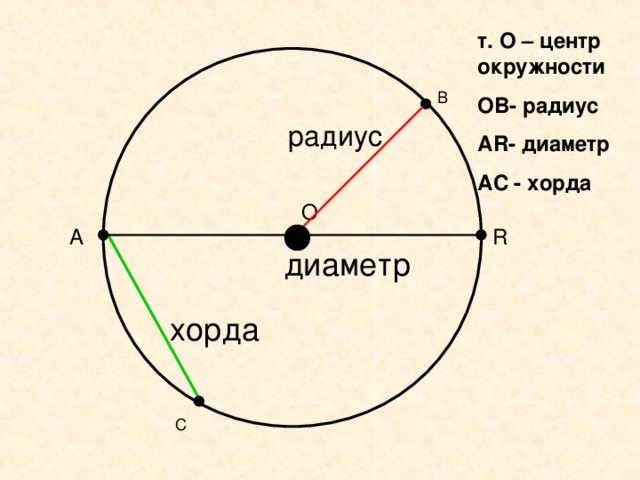
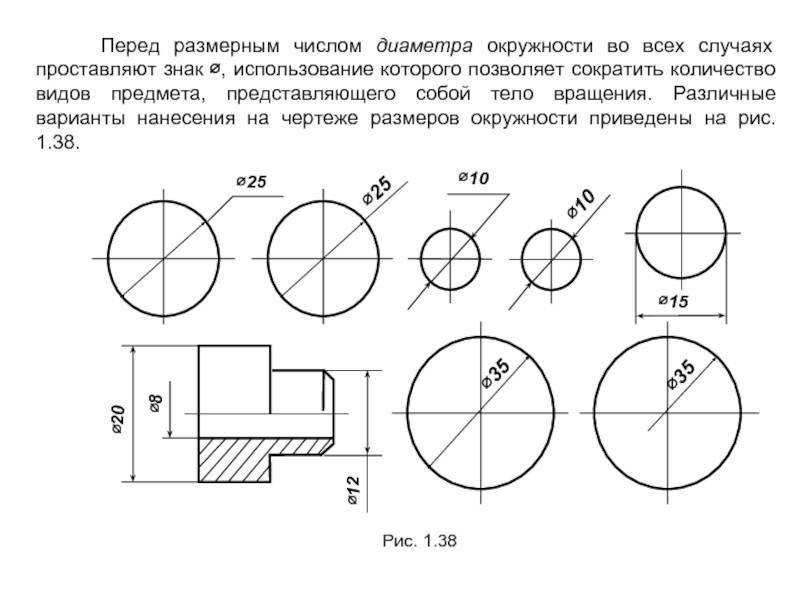
Какими символами помечают диаметр и радиус в графических изображениях

В графических изображениях, особенно в технических чертежах и диаграммах, диаметр и радиус обозначаются с помощью специальных символов. Эти символы позволяют легко распознать размеры и форму объектов на изображении. Давайте рассмотрим, какие символы используются для пометки диаметра и радиуса.

Символы для обозначения диаметра

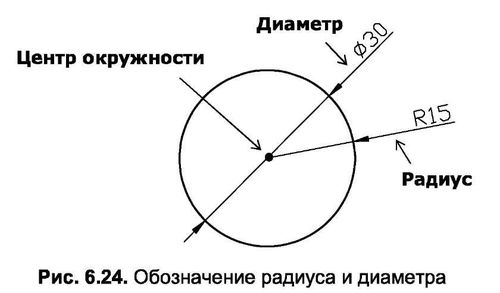
Диаметр, в графических изображениях, обозначается символом «⌀» или латинской буквой «D». Эти символы часто располагаются перед числовым значением диаметра. Например, «⌀10» или «D10» означает диаметр равный 10 единицам измерения.

Символы для обозначения радиуса

Радиус, в графических изображениях, обозначается символом «R» или латинской буквой «R» в верхнем регистре. Эти символы также часто располагаются перед числовым значением радиуса. Например, «R5» означает радиус равный 5 единицам измерения.

Форматы обозначения

Для более ясной и понятной пометки размеров диаметра и радиуса, часто используется следующий формат:

1. Символ обозначения (⌀ или D для диаметра, R для радиуса)
2. Значение размера
3. Единицы измерения (если применимо)

Например, «⌀10 мм» или «R5 см» являются примерами полного обозначения диаметра и радиуса с указанием единиц измерения.

Примеры использования символов

В таблице приведены примеры использования символов для обозначения диаметра и радиуса:

Тип объекта	Символ диаметра	Символ радиуса
Круг	⌀	R
Цилиндр	⌀	R
Сфера	⌀	R
Кольцо	⌀	R

Как видно из примеров, символ диаметра и радиуса часто совпадают для разных типов объектов. Это упрощает восприятие и сокращает затраты на разработку и печать графических изображений, так как необходимо использовать только два символа.

В заключение, символы для обозначения диаметра и радиуса в графических изображениях играют важную роль в инженерных и научно-технических отраслях. Правильное использование этих символов помогает представить информацию о размерах объектов более понятным и легким для восприятия способом.

Как радиус отличается от диаметра

Радиус окружности — это расстояние от центра окружности до любой точки на его границе. Он обозначается символом «r». Радиус является половиной диаметра и имеет ту же длину как для любой точки на окружности, так и для центра. Радиус является важным параметром при решении различных задач, например, при вычислении площади или длины окружности.

Диаметр окружности — это наибольшее расстояние между двумя точками на его границе. Он обозначается символом «d» и является удвоенным радиусом окружности. Другими словами, диаметр — это отрезок, соединяющий две противоположные точки границы окружности и проходящий через ее центр. Диаметр также играет важную роль в геометрии, особенно при решении задач, связанных с измерением, углом поворота и другими характеристиками окружности.

Таким образом, радиус и диаметр окружности — это два ключевых параметра, которые позволяют определить размеры и форму окружности. Радиус определяет расстояние от центра до точки границы, в то время как диаметр определяет наибольшее расстояние между двумя точками границы. Понимание разницы между радиусом и диаметром поможет вам использовать правильные формулы и методы для решения задач, связанных с окружностями.

Какая формула найти радиус?

радиус всегда половина длины его диаметра.

1. Например, если диаметр 4 см, радиус равен 4 см ã · 2 = 2 см.
2. В математических формулах радиус равен r, а диаметр d. Вы можете увидеть этот шаг в своем учебнике как r = d 2 {displaystyle r = {frac {d} {2}}}.

Как решать радиус и диаметр?

Возьмите окружность круга и разделите его на PI. Например, если окружность составляет 12,56, вы бы разделили 12,56 на 3.14159, чтобы получить 4, что является диаметром круга. Используйте диаметр, чтобы найти радиус, разделяя диаметр на 2 . Например, если диаметр 4, радиус будет 2.

Какую формулу найти диаметр?

Формула, чтобы найти диаметр, устанавливает взаимосвязь между диаметром и радиусом. Диаметр состоит из двух сегментов, каждый из которых является радиусом. Следовательно, формула: diameter = 2 * Измерение радиуса . Вы можете сократить эту формулу как d = 2r.

Почему радиус – половина длины диаметра?

Радиус круга – это длина сегмента линии от центра круга до точки на окружности круга, а диаметр – это линейный сегмент от одного конца круга до круга до круга до круга другой конец круга проходит через центр круга. Итак, радиус наполовину длины диаметра.

Как найти радиус без диаметра?

Просто помните , чтобы разделить диаметр на два до Получить радиус. Если бы вас попросили найти радиус вместо диаметра, вы просто разделили бы 7 футов на 2, потому что радиус наполовину мера диаметра.

Advertisements

какова длина радиуса круга?

Объяснение: Определение радиуса круга – это длина сегмента линии от центра круга до точки на окружности круга. Итак, радиус половина длины диаметра .

Как вы преобразовываете радиус в длину?

Разделите центральный угол на радиан на 2 и выполните синусную функцию на нем. Разделите длину аккорда, вдвое больше, чем Шаг 1. Этот расчет дает вам радиус. Умножьте радиус на центральный угол, чтобы получить длину дуги.

Диаметр круга

Диаметр составляет длина линии через центр, который касается двух точек на краю круга .

какая половина длины круга?

В математике (и более конкретно геометрии) полукруга является одномерным локусом точек, которые образуют половину круга. Полная дуга полукруга всегда измеряет 180 ° (эквивалентно, € redians или полворот).

Радиус аккордом?

радиус: радиус круга – расстояние от центра его центра до точки на круге – рассказывает вам размер круга. В дополнение к меру расстояния, радиус также является сегментом, который переходит от центра круга до точки на круге. Аккорд: сегмент, который соединяет две точки на круге, – это , называемый аккордом.

Как выглядит диаметр?

В геометрии диаметр круга – это любой сегмент прямой линии , который проходит через центр круга и чьи конечные точки лежат на круге. Это также может быть определено как самый длинный аккорд круга. Оба определения также действительны для диаметра сферы.

Как найти внешний диаметр?

Измерьте или рассчитайте внешнюю окружность трубы. Затем разделите эту сумму на pi , обычно округлый до 3,1415. Результатом является внешний диаметр трубы.

Диаметр: сущность и определение

Для определения диаметра необходимо знать радиус окружности, так как диаметр всегда в два раза больше радиуса. Диаметр обозначается символом «d» и является одной из основных характеристик окружности, вместе с радиусом, центром и длиной окружности.

Диаметр широко используется в различных областях науки и техники. Например, в строительстве и проектировании он помогает определить размеры круглых объектов, в медицине — для измерения сосудов и образований, а также в физике — для вычисления площади и объема.

Отличие диаметра от радиуса заключается в том, что радиус — это расстояние от центра окружности до ее границы, а диаметр — это отрезок, который проходит через центр и удваивает радиус. Таким образом, диаметр является удобной характеристикой, позволяющей определить размеры окружности и ее свойства.

Важно отметить, что диаметр является основным параметром окружности и играет важную роль в решении задач, связанных с геометрией и различными научными и техническими областями знания

Что такое диаметр окружности?

Диаметр окружности является важным параметром для определения других свойств и характеристик окружности. Например, диаметр окружности равен удвоенному радиусу. Он также служит основой для расчета площади и длины окружности.

Диаметр окружности можно измерить при помощи линейки или другого измерительного инструмента, проводя его через центр окружности и измеряя расстояние между двумя противоположными точками.

Также следует отметить, что диаметр окружности является симметричным относительно центра окружности. Это означает, что при отражении диаметра относительно центра, его конечные точки не изменятся.

Окружность и круг

Круг — это замкнутая плоская кривая, состоящая из всех точек плоскости, равноудаленных от определенной точки. Эта точка называется центром окружности. Линия, соединяющая центр и точки на окружности, называется радиусом. Длина линии также называется радиусом.

Окружность — это часть плоскости, которая лежит внутри окружности. Другими словами, это совокупность точек на плоскости, расстояние которых от определенной точки, называемой центром окружности, не превышает определенного неотрицательного числа. Номер. Это называется радиусом круга.

Определение окружности и круга

Значение. Круг — это фигура, состоящая из всех точек плоскости на определенном расстоянии от определенной точки.

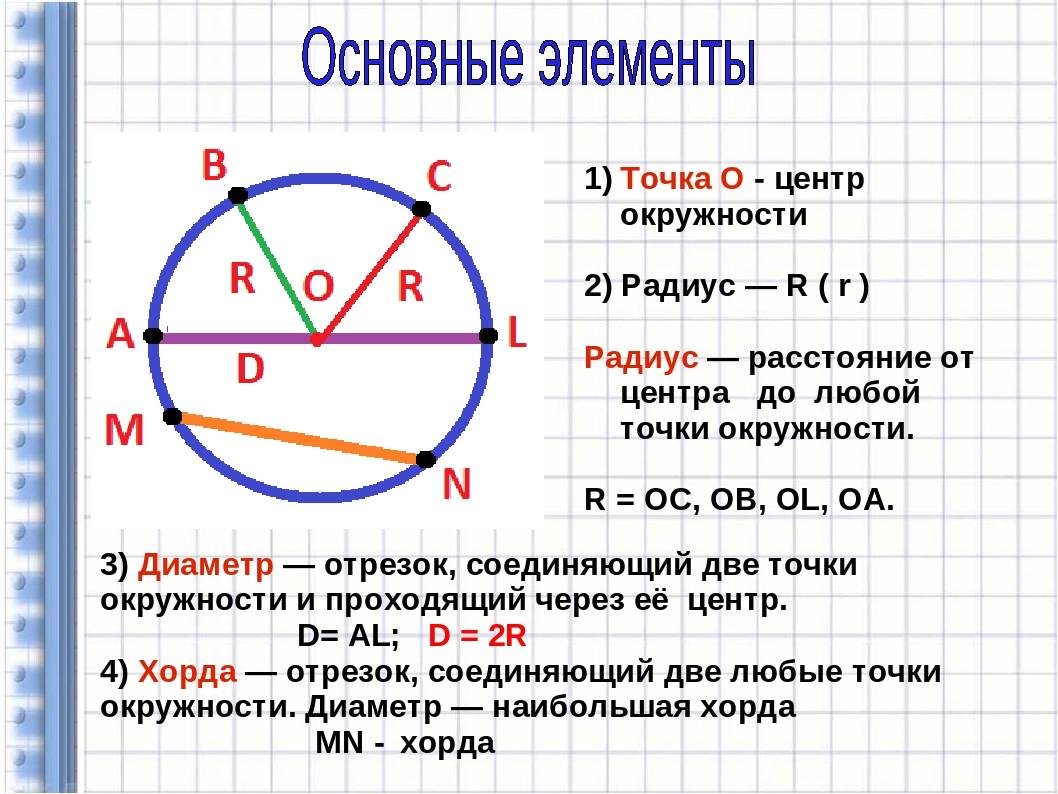
Эта точка называется центром окружности. Расстояние точки от центра окружности называется радиусом окружности. Радиусом также называется часть окружности, соединяющая точку и ее центр.

Значение. Часть окружности, соединяющая две точки, называется струной. Нить, проходящая через центр, называется диаметром.

На рисунке 2.151 изображена окружность с центром в точке O. Отрезок OA — радиус окружности, BD — строка окружности, а CM — диаметр окружности.

Значение. Окружность — это фигура, состоящая из всех точек плоскости на расстоянии, меньшем или равном одной конкретной точке.

Эта точка называется центром окружности, а это расстояние — радиусом окружности. Граница окружности — это окружность, центр и радиус которой совпадают (рис. 2.152).

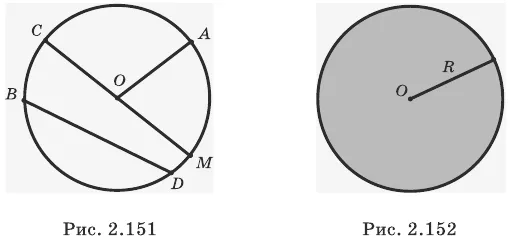
Пример:

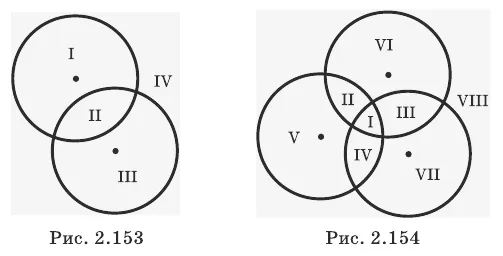
Какое максимальное количество различных отрезков, не имеющих ничего общего, кроме своих границ, может разделить уровень на a) две окружности и b) три окружности?

Используйте эту диаграмму, чтобы показать соответствующий случай согласования. Запишите ответы: а) четыре сегмента (рис. 2.153) — б) восемь сегментов (рис. 2.154).

Центральные углы и дуги окружности

Предположим, что вершина угла совпадает с центром окружности (рис. 2.155). Угол AOB называется центральным углом.

Определение. Центральный угол окружности — это плоский угол с центром в вершине.

Внутренняя круговая часть угла называется дугой окружности, соответствующей этому центральному углу.

Значение. Пересечение окружности и ее центрального угла называется дугой окружности.

Мера градуса дуги окружности равна мере градуса соответствующего центрального угла.

Градусная мера дуги АВ на рисунке 2.155 равна градусной мере угла АОВ. Градусная мера дуги АВ обозначается

Можно ввести еще одну важную единицу дуги. При измерении углового значения дуги окружности единицей измерения является угловое значение этой дуги окружности, длина которой равна радиусу окружности. Эта единица измерения размера угловой дуги называется радиусом.

Сформулируем некоторые свойства измерения дуги окружности.

-Измеренный порядок дуги не зависит от размера окружности.

-Соответствующие дуги двух концентрических окружностей на рис. 2.156 имеют одинаковый порядок (размер).

-По мере увеличения размера дуги (в пределах определенной окружности) ее мера также увеличивается.

Окружности (или круги) равны, если у них равные радиусы. Мы можем говорить о равных дугах, но равная дуга может быть либо одной окружностью, либо равной окружностью.

Значение. Две дуги одинаковых или равных окружностей называются равными, если они имеют одинаковую степень меры.

Определение диаметра и радиуса

В геометрии и геометрической топологии, диаметр и радиус относятся к основным понятиям, которые используются для измерения размера и пространственной характеристики геометрических объектов.

Диаметр — это расстояние между двумя точками на окружности или сфере, проходящее через их центры. Другими словами, диаметр — это самое длинное расстояние между двумя точками на окружности или сфере. Для окружности диаметр — это двойная длина радиуса.

Радиус — это расстояние от центра окружности или сферы до любой точки на ее поверхности. Радиус измеряется от центра геометрического объекта до любой его точки и используется для определения размера и формы окружности или сферы.

Диаметр и радиус неразрывно связаны друг с другом. Для любого геометрического объекта с заданным радиусом, диаметр всегда будет в два раза больше. Математически, диаметр равен умноженному на 2 значению радиуса.

Как правило, диаметр и радиус используются для измерения окружностей, сфер и других кривых объектов, которые обладают центральной точкой. Они являются важными параметрами для вычисления площади, объема, длины дуги и других характеристик геометрических фигур и тел.

Основные формулы для вычислений

Параметры используются в формулах вычислений величин окружности:

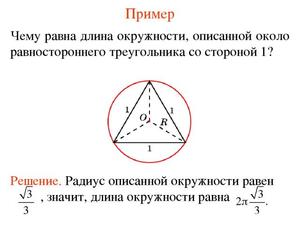
Диаметр в формулах вычисления

В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С – это искомая величина, D – диаметр.

Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере – длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.

Расчёты по радиусу

Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С – длина, r – радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.

Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?

Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.

Подручные способы вычисления

Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:

• При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
• Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
• Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.

Определения и свойства окружности

Введем несколько определений, связанных с темой окружности. Данные термины можно встретить на уроках в седьмом классе и других курсах по алгебре и геометрии.

1 Примечание 1

В распространенных случаях возникает путаница в понятиях окружности и круга. Заметим, что кругом может называться множество точек на плоскости, которые при построении ограничены окружностью, то есть данные точки расположены во внутренней области окружности.

Окружность обладает рядом свойств:

1. Если три точки на плоскости не принадлежат общей прямой, то через них допустимо построить единственную окружность.
2. Точка (С), в которой касаются две окружности, расположена на общей с центрами этих окружностей прямой (АВ).
3. Изопериметрическое неравенство: из всех замкнутых кривых на графике, имеющих одинаковую длину, окружность ограничивает область с максимальной площадью.

При решении самостоятельных работ и задач на некоторые окружности пригодятся следующие формулы, чтобы находить ключевые параметры:

Диаметр окружности можно высчитать таким образом:

Длина окружности в теории:

Радиус окружности можно узнать с помощью формулы:

Характеристики фигуры

Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две – А и В – можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.

В пределах окружности имеются точки Х такие
, что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.

Основные термины окружности

Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры – это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр – расстояние между точками
, проходящее через центр фигуры.

Дуга окружности

Дугу можно измерять не только в единицах измерения длины, но и в градусах. Вся дуга окружности имеет градусную меру 360\(\circ\). Тогда половина дуги окружности будет равняться 180. 

При этом дуга, равная 180\(\circ\), называется полуокружностью. Полуокружность ограничивается двумя концами диаметра.  

Думаем, хоть раз в жизни вы слышали  фразу “повернуться на 180\(\circ\) градусов” или “поменять свое мнение на 180\(\circ\) градусов”. Это означает, что человек меняет свое мнение буквально на противоположное. Рассмотрим на примере окружности: пусть человек стоит в точке А. Ему нужно пройти по окружности ровно 180\(\circ\). 

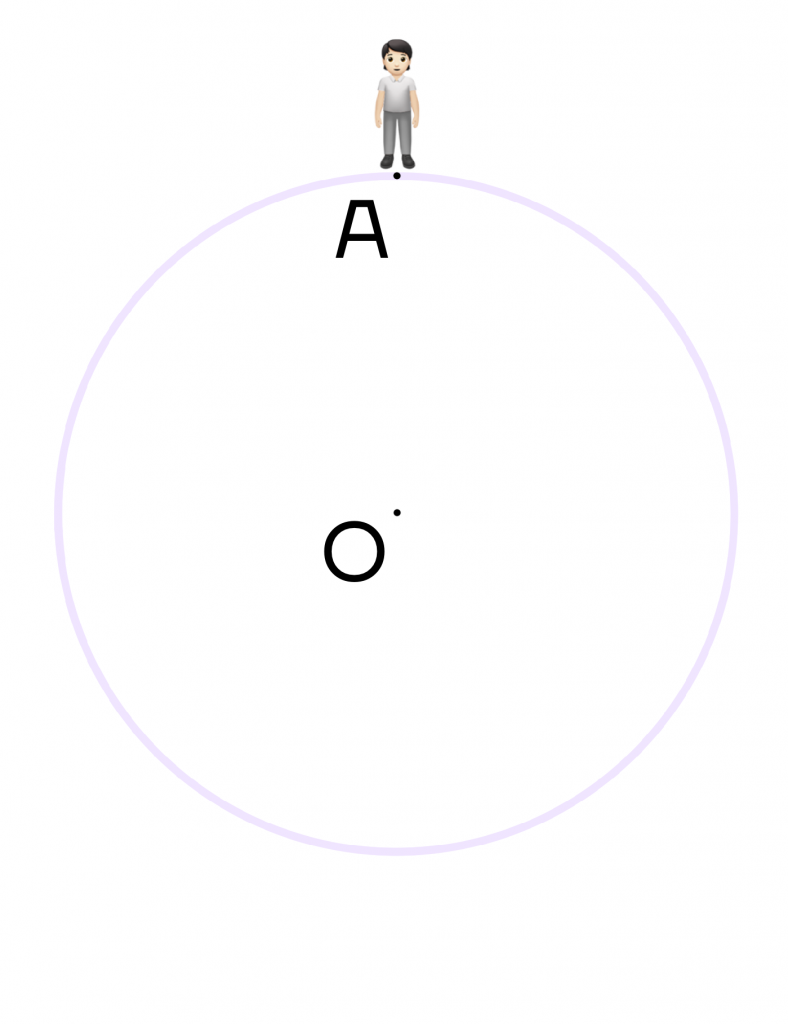
Поскольку человеку нужно пройти полуокружность, то она ограничивается диаметром. Достроим диаметр АВ, тогда наш человек окажется в точке В, то есть на противоположной стороне окружности. 

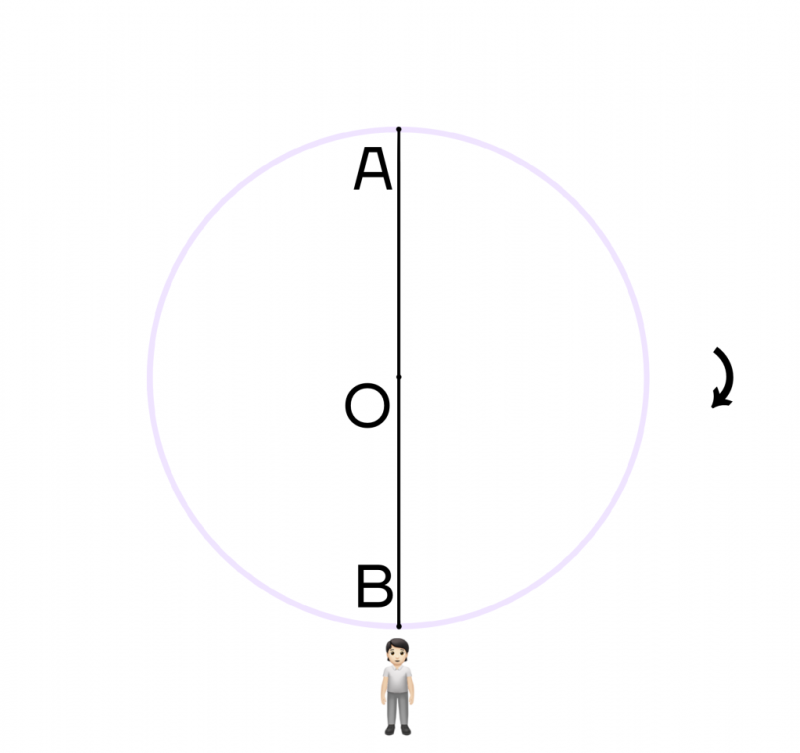
А если он дважды пройдет полуокружность, то снова окажется в точке А, то есть пройдет дугу в 2 * 180 = 360 градусов.

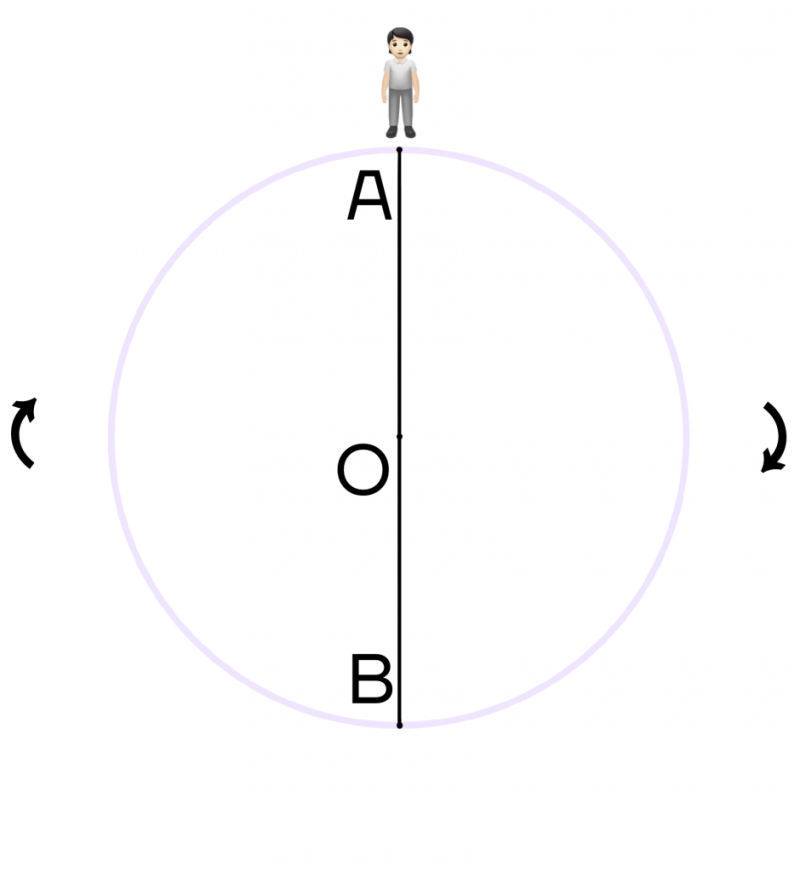
Поэтому если человек будет находиться в точке О и захочет повернуться на 180 градусов, то вместо точки А он будет смотреть на точку В. При повороте на 360 градусов, человек снова будет смотреть на точку А. 

Почему если мы хотим что-то сильно поменять, то лучше разворачивать жизнь на 180 градусов, а не на 360? При повороте на 180 градусов, мы смотрим на что-то с совершенно противоположной стороны. А вот если повернуться на 360 градусов, то мы будем смотреть на ту же точку, на которую смотрели изначально.

Сопряженные знаки диаметра и радиуса

В математике и физике у размерностей диаметра и радиуса есть сопряженные знаки, которые используются для их обозначения.

Диаметр обозначается символом d, а радиус обозначается символом r. Они являются основными размерностями для окружности и используются в различных формулах и уравнениях.

Знаки диаметра и радиуса в примерах

Ниже приведены некоторые примеры использования знаков диаметра и радиуса:

1. Диаметр окружности равен удвоенному радиусу: d = 2r
2. Площадь окружности можно выразить через радиус: S = πr^2
3. Длина окружности зависит от диаметра: L = πd

Таблица сопряженных знаков диаметра и радиуса

Описание	Диаметр	Радиус
Обозначение	d	r
Формула	d = 2r	r = d/2

Таким образом, знаки диаметра и радиуса являются основными символами и размерностями, которые используются для обозначения размеров окружности и связанных с ней величин в математике и физике.

Как начертить радиус на чертеже

Чтобы начертить радиус на листе необходимо воспользоваться таким инструментом как циркуль. С помощью линейки циркулем отмеряют радиус, размер которого известен заранее. Устанавливают острие циркуля в центр будущей окружности и проводят сектор, часть дуги или окружность целиком в зависимости от условий задачи. Обратным действием можно найти радиус, зная где находится центр окружности. Определить диаметр можно, зная радиус круга, для этого нужно его значение увеличить в два раза. Также, зная длину контура окружности, можно вычислить радиус или диаметр через число Пи.

При построении радиуса на компьютере воспользуемся соответствующим инструментом на панели, обычно можно начертить окружность по заданному центру и значению, начертить сектор или дугу ограничив ее на плоскости. Вводя нужные значения и указав точку на плоскости, программа сама построит окружность по радиусу. Чтобы соединить отрезки с помощью радиуса используется инструмент «Сопряжение». Необходимо выбрать отрезки, а программа сама подберет нужный радиус. Эта функция очень удобна, когда необходимо соединить два элемента, располагающихся под углом, к примеру стены дома на плане или полку и стенку двутавра на чертеже.

Радиусы можно начертить в любой программе векторной графики, начиная от Корел Дро, заканчивая Автокадом, Ревитом, Компасом и Архикадом. Линейный размер наносится после того, как сам элемент вычерчен, через инструмент «Размеры», расположенный в основном меню. Через свойства можно изменить высоту текста, тип оформления концов отрезков, толщину и прочее.

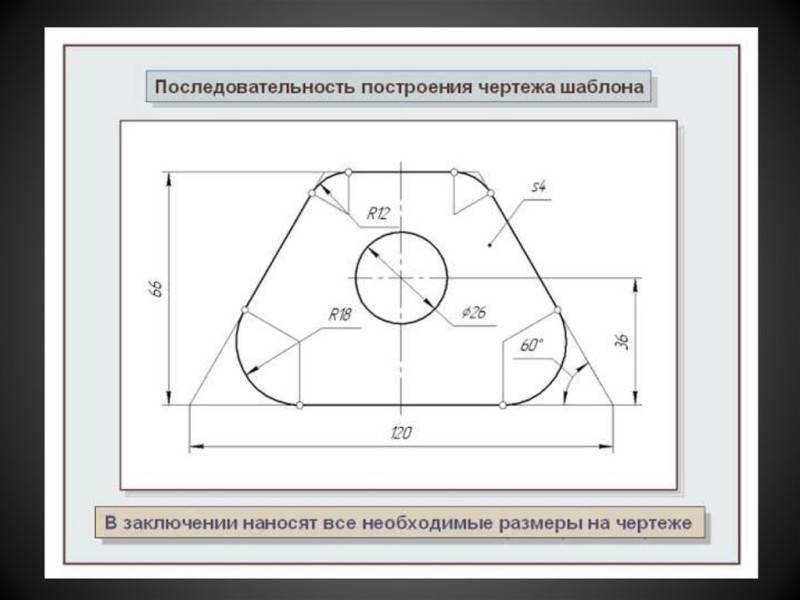Рисунок 3. Как начертить радиус на чертеже

Радиусы и диаметры на чертеже по ГОСТу

Традиционно, в пояснительных записках и на чертежах используется условное обозначение радиуса латинской буквой R. После этого символа идет размерное число.

Отрезок начинается от центра окружности, на конце отрезка рисуется стрелка, направленная к самой окружности.

Бывают случаи, когда значение радиуса велико и поэтому линию приближают к дуге и показывают с изломом под 90 градусов.

Также зачастую исполнителю нет необходимости показывать центр окружности, особенно если размер очень большой и составляет несколько метров, поэтому сам отрезок не доводят до центра.

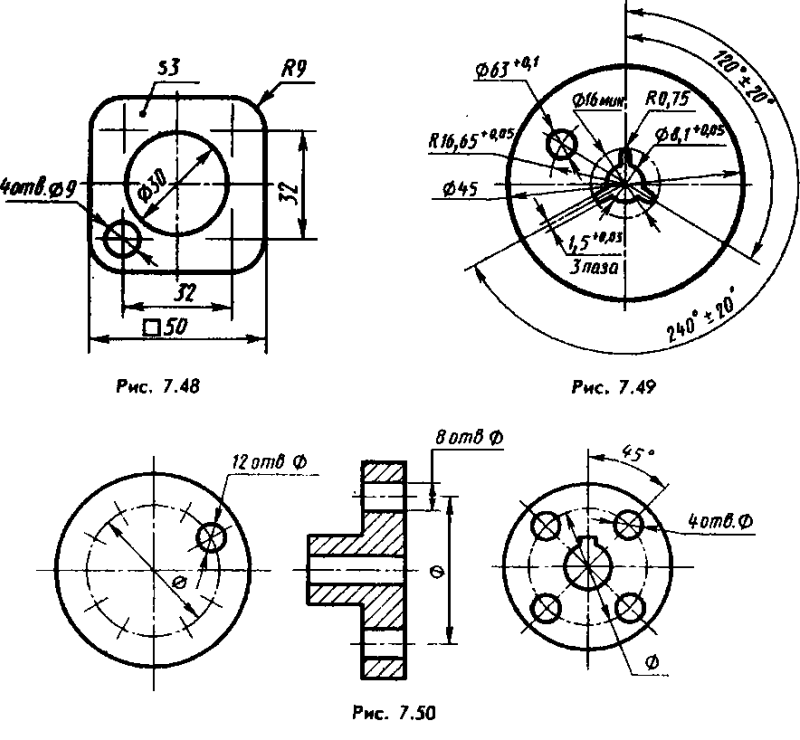Рисунок 2. Радиусы и диаметры на чертеже по ГОСТу

Диаметр и радиус: основные различия

Диаметр окружности — это отрезок, проходящий через ее центр и соединяющий любые две точки на окружности. Длина диаметра равна удвоенной длине радиуса.

Радиус окружности — это отрезок, соединяющий центр окружности с любой точкой на ее окружности. Радиус является половиной длины диаметра и обозначается символом «r».

• Диаметр определяет самую большую возможную длину отрезка на окружности, и он всегда проходит через центр окружности.
• Радиус, в свою очередь, определяет расстояние от центра окружности до любой точки на окружности.
• Диаметр и радиус являются взаимно связанными величинами и не могут существовать независимо друг от друга.
• Диаметр и радиус используются для вычисления других характеристик окружности, таких как площадь и длина окружности.

Понимание различий между диаметром и радиусом позволяет более точно описывать и анализировать геометрические свойства окружностей и применять их в различных областях, таких как физика, инженерия и геометрия.

Применение радиуса и диаметра

Радиус – это расстояние от центра окружности (или сферы) до любой ее точки. Обозначается символом r.

Диаметр – это отрезок, проходящий через центр окружности (или сферы), и связывающий две противоположные точки на ее границе. Диаметр равен удвоенному значению радиуса. Обозначается символом d.

Радиус и диаметр находят широкое применение в различных областях:

• Геометрия: радиус и диаметр используются для расчетов и построений окружностей, а также для определения различных свойств и параметров фигур.
• Физика: радиус часто используется для измерения размеров частиц и атомов, а диаметр – для определения межчастичных расстояний и характеристик объектов.
• Инженерия: радиус и диаметр применяются для расчета размеров и формы деталей, а также для оценки прочности и устойчивости конструкций.
• Медицина: радиус и диаметр используются для измерения размеров органов и структур внутри организма, а также для определения диагностических параметров.
• Компьютерная графика: радиус и диаметр применяются для построения и отображения геометрических объектов, моделей и анимаций.

Знание радиуса и диаметра является важным при решении различных задач и проблем, связанных с геометрией и математикой, а также во многих других научных и технических областях.

Взаимное отношение хорд и их расстояний от центров

Изобразим окружность и ее элементы, согласно теореме:

Заметим, что радиус, обозначенный, как OC, расположен перпендикулярно к хорде AB, как показано на рисунке:

.

Попробуем доказать следующее:

.

Проведем прямую через точки А и В, которая соединит их с центральной точкой О. Заметим, что наклонные OA и OB равны и удалены от перпендикулярной прямой ОС. В результате:

AD = DB.

Предположим, что перпендикулярная прямая CD выходит из середины AB. В таком случае, точка C равноудалена относительно концов перпендикуляра. Из этого следует равенство хорд AC и CB. Таким образом:

.

Получаем, что перпендикуляр OC делит на две равные части дугу AB, что и требовалось доказать.

Начнем доказательство данного утверждения с того, что центральная точка равноудалена от концов хорды. В таком случае, она будет расположена на перпендикуляре, который восстановлен из середины хорды, что и требовалось доказать.

Перенесем данные на рисунок:

Запишем равенство двух хорд AB и CD:

AB = CD

Представим доказательство того, что данные хорды расположены на одинаковом расстоянии от центральной точки:

OE = OF

Если соединить между собой точки A и C, а также центральную точку O, получим пару треугольников AEO и COF, которые равны и являются прямоугольными. Объясним это равенством радиусов:

OA = OC.

Заметим также, что половины одинаковых хорд будут равны друг другу:

AE = CF.

В результате получим доказательство теоремы:

OE = = OF.

Воспользуемся предыдущим рисунком. Запишем, что хорды AB и CDравноудалены от центра:

OE = OF.

Попробуем подтвердить справедливость следующего равенства:

AB = CD.

Рассмотрим пару прямоугольных треугольников AEO и COF. Данные треугольники равны, исходя из равенства гипотенуз и катетов. Согласно условию:

OE = OF

Равенство радиусов:

OA = OC.

В результате получим, что:

AE = CF

Таким образом, теорема доказана:

AB = CD

Заметим, что хорда AB больше по сравнению с хордой AC:

AB > AC

Требуется доказать следующее:

OD < OE

Заметим, что OD расположен перпендикулярно относительно AB. Линия OF является наклонной. В таком случае:

OD < OF

Запишем, что:

OF < OE

В результате теорема доказана:

OD < OE

Выводы

Круг – плоская, двухмерная фигура. Шар – объемное трехмерное геометрическое тело. Тем не менее, они имеют массу сходств (наличие ограничивающей поверхности, диметра и радиуса, наполненность структуры в отличие от той же окружности, возможност вычислить площадь).

Чем же отличается круг от шара? Круг плоский, шар же имеет объем. Именно объемность шара позволяет ему делиться на сечения, которые по своей сути являются кругами. Круг, напротив, делится на сектора.

Публикации по теме:

Детско-родительский игровой сеанс «Круг» для детей ОВЗ Игровое занятие КРУГ для детей ОВЗ Тема «Осень. Природные явления» Цели и задачи занятия КРУГ Главная цель занятия КРУГ – дать каждому ребенку.

Конкурс профессионального мастерства «Солнечный круг» (фотоотчет) С 12 по 26 октября 2015 года в нашем детском саду проходил конкурс профессионального мастерства «Воспитатель года». Цель конкурса: выявление.

Конспект НОД по ФЭМП «Знакомьтесь: круг» Конспект НОД по ФЭМП во второй младшей группе «Знакомьтесь- круг» Цель: развитие познавательных интересов детей Задачи: Познакомить.

НОД по математике «Круг и квадрат» (младшая группа) Тема: «Круг и квадрат» (младшая группа) Образовательная область: познание Цель: Продолжать учить находить один и много предметов в специально.

Поделки в технике «объемный квиллинг» Здравствуйте, коллеги! Недавно открыла для себя технику объемного квиллинга. Искусство, которое на русском языке называют «бумагокручением»,.

Проект по математическому развитию «Круг, квадрат и треугольник-фигуры важные, фигуры нужные» Номинация проекта – «Дошкольный возраст» Вид проекта: долгосрочный, фронтальный. Участники проекта: подгруппа детей средней группы, воспитатель.

«Снежинка 3-D». Объемный модуль для украшения интерьера Приближаются Новогодние праздники и перед нами, как воспитателями опять стоит вопрос «Чем же удивить детей и взрослых?». Просторы Интернета.

Совместная образовательная деятельность по ФЭМП «Круг и квадрат» Совместная образовательная деятельность взрослого и детей ФЭМП «Круг и квадрат». Цель: закреплять умение различать и называть круг и квадрат.

Весенний объемный тюльпан на открытке в подарок маме Не за горами прекрасный весенний праздник 8 Марта. И уже сейчас многие педагоги задумались над тем, что бы смастерить с детьми мамам в.

На уроках геометрии в школе все мы изучали свойства различных фигур и линий. Каждая из них имеет свои особенности, а порой некоторые из них взаимосвязаны друг с другом. Взять для примера хотя бы круг и окружность – между ними есть определенная связующая линия. Только вот какая? Давайте вместе разберемся в этом вопросе.Окружность
представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности. Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность. Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится. По этой причине имеется четкое понятие, что окружность делит всю плоскость на две части – внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, поскольку плоскость в общем понимании не имеет границ.Круг
является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность. Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.
Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии. Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга. Иными словами, круг представляет собой не только окружность, которая является его границей, но также и то бесконечное число точек, находящихся внутри этой окружности.