Разница между площадью и периметром

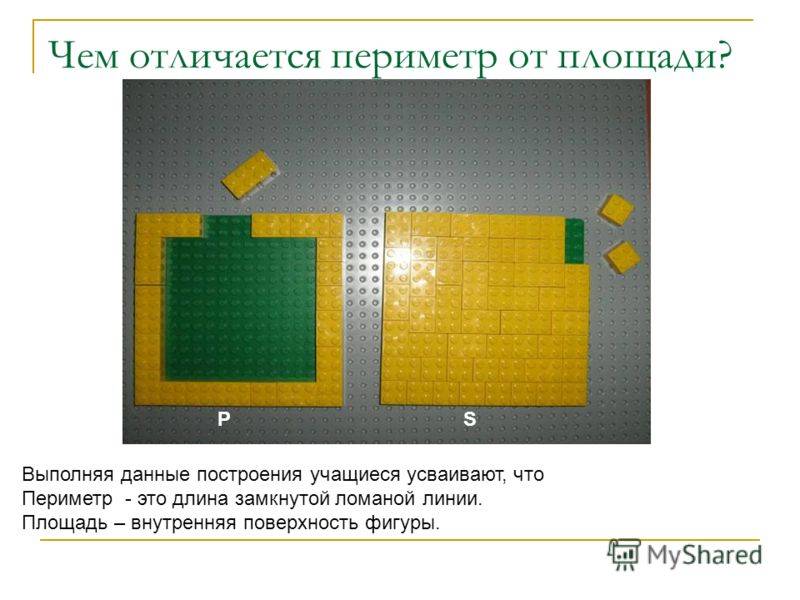
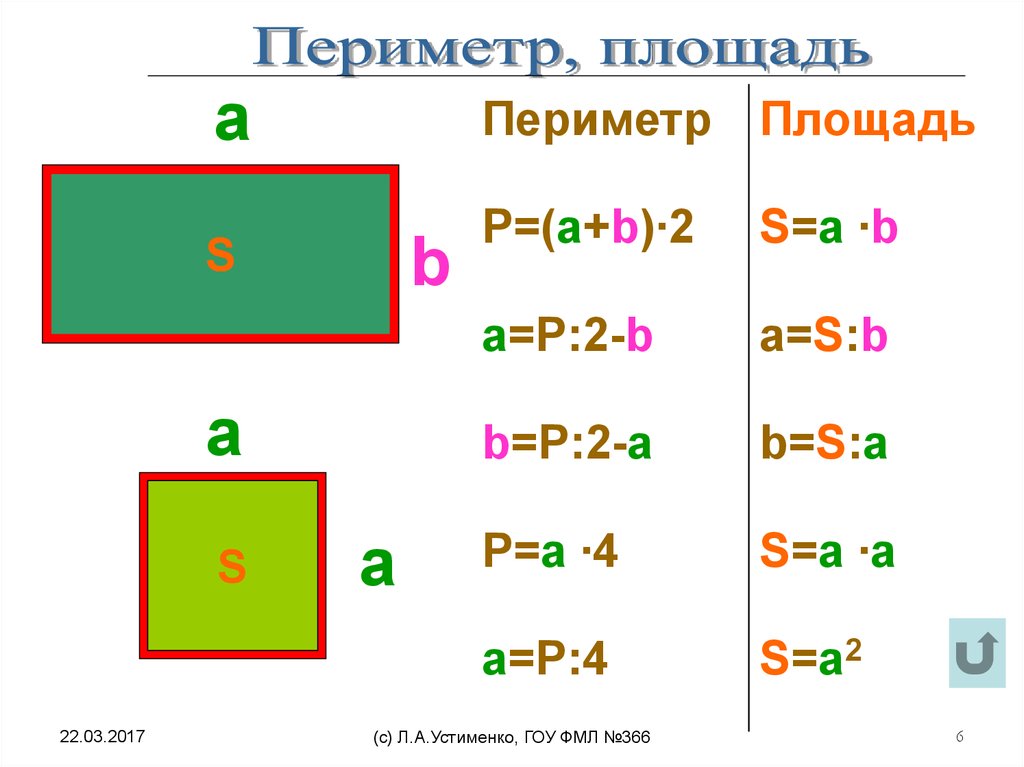
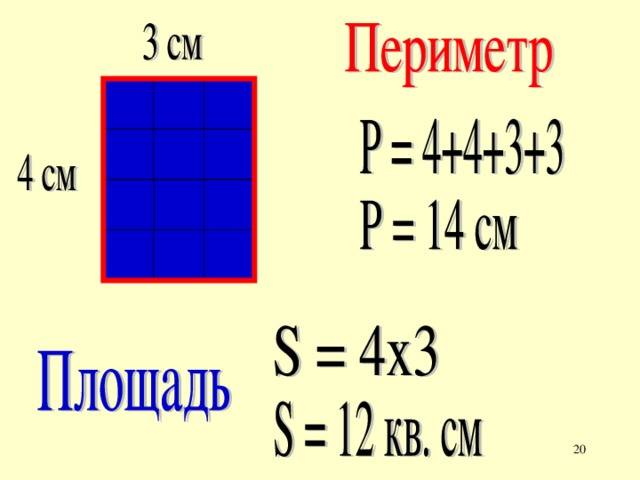
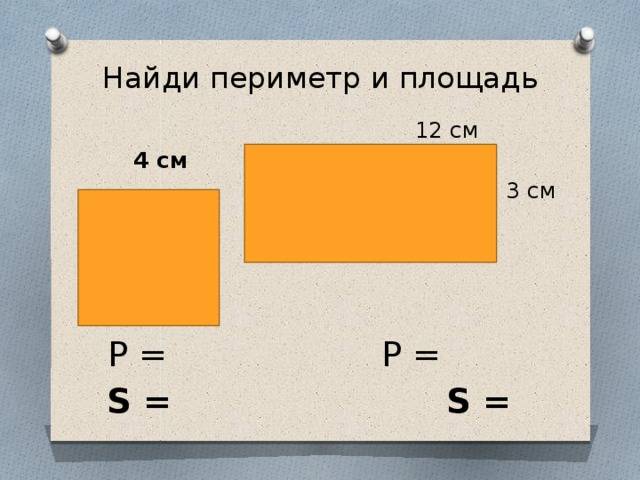
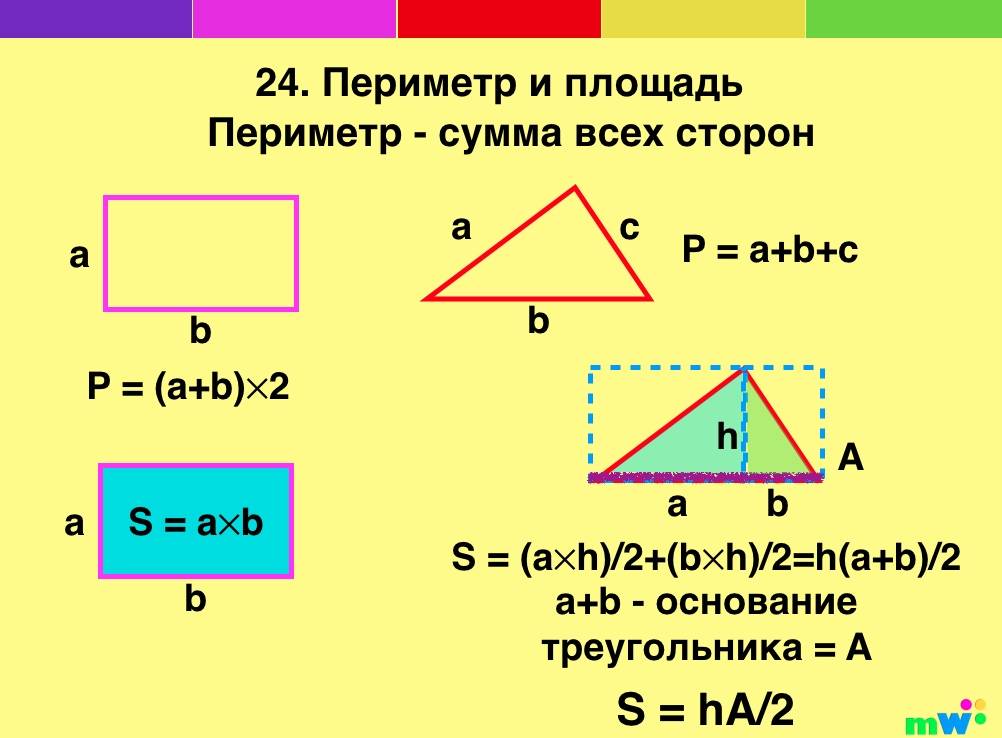
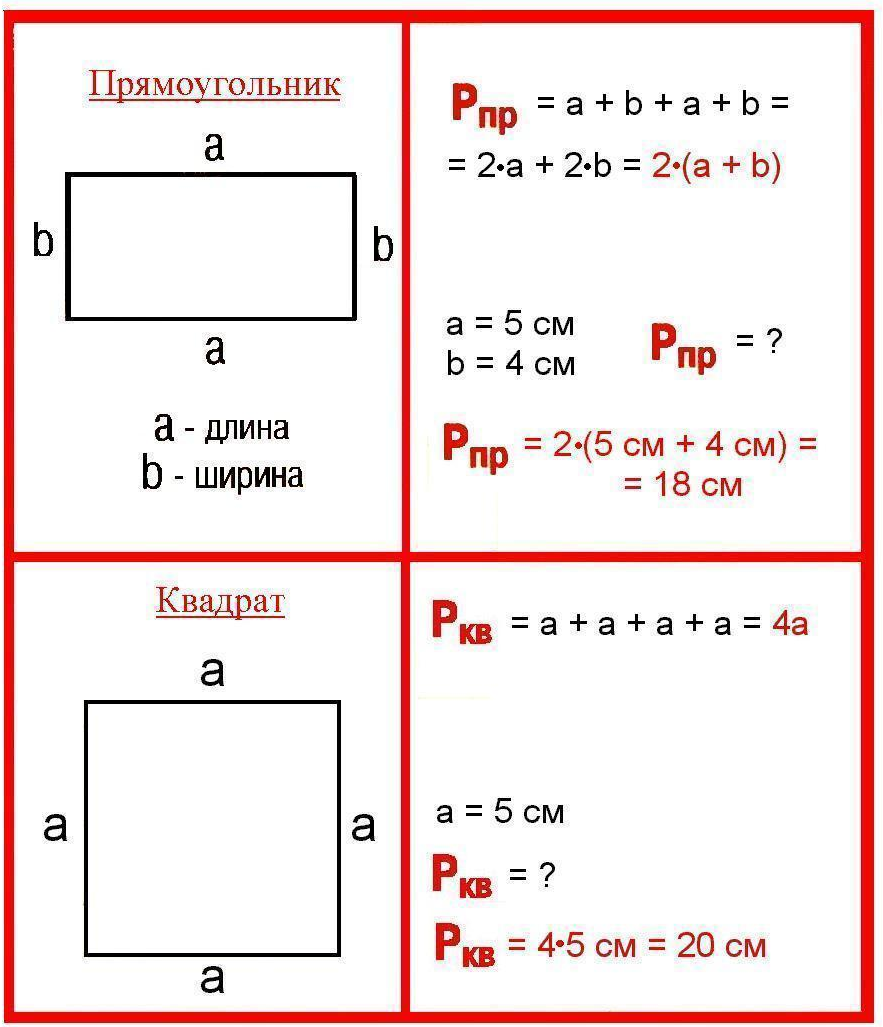
Содержание: Площадь по периметру

1. Сравнительная таблица
2. Определение
3. Ключевые отличия
4. Формулы
5. Вывод

Сравнительная таблица

Основа для сравнения	Площадь	периметр
Смысл	Площадь описывается как измерение поверхности объекта.	Периметр относится к контуру, который окружает замкнутую фигуру.
Представляет	Пространство, занимаемое фигурой.	Обод или граница фигуры.
измерение	Квадратные единицы	Линейные единицы
Размеры участвуют	Два	Один
пример	Пространство в саду.	Длина забора, необходимого для ограждения сада.

Определение площади

В математике площадь плоской поверхности определяется как количество пространства, покрытого ею. Это физическая величина, которая указывает количество квадратных единиц, занимаемых двумерным объектом. Он используется, чтобы знать, сколько места занимает плоская поверхность. Он измеряется в квадратных единицах, то есть в квадратных метрах, квадратных милях, квадратных дюймах и т. Д..

Термин «область» имеет конечное число практического использования, например, в строительных проектах, сельском хозяйстве, архитектуре и так далее. Чтобы измерить площадь плоской поверхности, нужно посчитать количество квадратов, покрытых формой.

Например: Предположим, вам нужно выложить пол комнаты, количество плиток, необходимых для покрытия всей комнаты, будет его площадью..

Определение периметра

Периметр определяется как мера длины границы, которая окружает замкнутую геометрическую фигуру. Термин «периметр» происходит от греческого слова «Peri» и «метр», что означает вокруг и мера. В геометрии это подразумевает непрерывную линию, образующую путь за пределами двумерной формы.

Проще говоря, периметр – это не что иное, как длина контура фигуры. Чтобы узнать периметр конкретного объекта, вы можете просто прибавить длину сторон, чтобы получить его периметр. Периметр круга обычно известен как его окружность.

Например: а. Предположим, вы оберните строку вокруг квадрата, длина строки будет его периметром.б. Вы гуляете за пределами сада, пройденное расстояние будет периметром сада.

Что такое периметр?

Периметром называют суммарную длину всех сторон геометрической фигуры. Для его обозначения используется буква латинского алфавита «Р». Проще говоря, чтобы найти периметр, необходимо измерить длины всех сторон геометрической фигуры и сложить полученные значения. Длина вычисляется обычным измерительным прибором, таким как линейка, рулетка, сантиметровая лента и прочее.

Единицей измерения соответственно являются сантиметры, метры, миллиметры и другие меры длины. Длина стороны многоугольника вычисляется путем прикладывания измерительного прибора от одной вершины к другой. Начало шкалы деления прибора должно совпадать с одной из вершин. Второе числовое значение, на которое попадает другая вершина и является длиной стороны многоугольника. Таким же образом необходимо измерить все длины сторон фигуры и полученные значения сложить. Единицей измерения периметра является та же самая единица, которая используется для измерения стороны фигуры.

Прямоугольником следует называть геометрическую фигуру, которая состоит из четырех сторон разной длины и три угла у которой прямые. При построении такой фигуры на плоскости получается так, что стороны у нее будут попарно равны, но не равны все между собой. Что такое периметр прямоугольника? Это также суммарная длина всех длин фигуры. Но так как у прямоугольника по две стороны имеют одинаковое значение, то в вычислении периметра можно дважды сложить длины двух смежных сторон. Единицей измерения периметра прямоугольника также являются общепринятые единицы измерения.

Треугольником следует называть геометрическую фигуру, имеющую три угла (как разного значения, так и одинакового) и состоящую из отрезков, образованных от точек пересечения лучей, образующих углы. Треугольник имеет три стороны и три угла. В нем могут быть из трех равны две стороны. Такой треугольник следует считать равнобедренным. Бывают такие фигуры, в которых равны все три стороны между собой. Принято такие треугольники называть равносторонними.

Что такое периметр треугольника? Его вычисление можно провести по аналогии с периметром четырехугольника. Равен периметр треугольника суммарной длине длин его сторон. Вычисление периметра треугольника, в котором две стороны равны – равнобедренного – упрощается умножением одной длины равных сторон на два. К полученному значению необходимо прибавить значение длины третьей стороны. Вычисление периметра треугольника с равными сторонами можно свести к простому вычислению произведения одной длины стороны треугольника на три.

Таблица квадратов

В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.

Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.

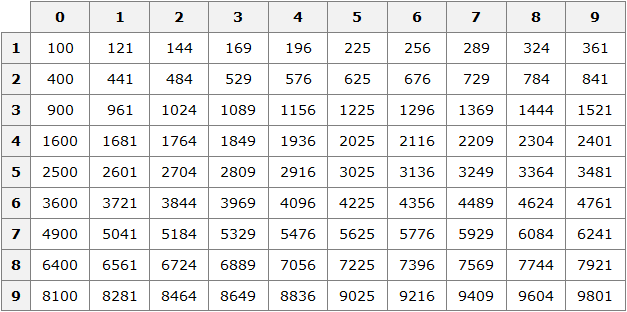
Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.

Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.

Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576

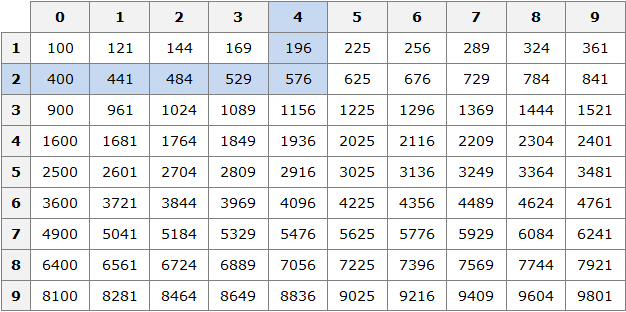
242 = 576

Использование в реальной жизни

1. Планирование строительства: периметр и площадь помогают инженерам и архитекторам правильно оценить размеры здания, посчитать необходимое количество строительных материалов и оценить стоимость проекта.

2. Построение забора: расчет периметра помогает определить длину ограждения, а расчет площади позволяет определить необходимое количество материала для его строительства.

3. Садоводство: площадь участка может помочь определить количество посадочных материалов (например, цветов или деревьев), а периметр может помочь определить размер ограждения.

4. Торговля: знание понятий периметра и площади может помочь оценить размеры товара и определить необходимое количество упаковок для его упаковки и доставки.

• 5. География: использование площади и периметра помогает изучать географические области, такие как размеры стран, объемы озер и площадь пустынь.
• 6. Искусство и дизайн: периметр и площадь могут использоваться в дизайне интерьеров и создании произведений искусства для достижения гармонии и баланса.
• 7. Спорт: понятия периметра и площади могут быть использованы для расчета размеров спортивных площадок и соревновательных площадей.

Это только несколько примеров, где знание периметра и площади может быть применено. В реальной жизни эти концепции имеют широкое применение и могут быть полезны в различных сферах деятельности.

Задания для самостоятельного решения

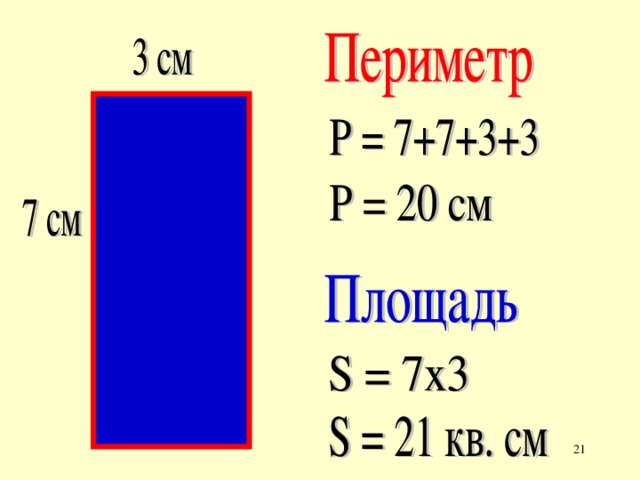
Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.

Решение

P = 2(a + b)

a = 6, b = 2P = 2(6 + 2) = 12 + 4 = 16 см

Ответ: периметр прямоугольника равен 16 см.

Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.

Решение

S = aba = 6, b = 2S = 6 × 2 = 12 см2

Ответ: площадь равна 12 см2.

Задача 3. Площадь прямоугольника составляет 12 см2. Длина составляет 6 см. Найдите ширину прямоугольника.

Решение

S = abS = 12, a = 6, b = x12 = 6 × xx = 2

Ответ: ширина прямоугольника составляет 2 см.

Задача 4. Вычислите площадь квадрата со стороной 8 см

Решение

S = a2a = 8S = 82 = 64 см2Ответ: площадь квадрата со стороной 8 см равна 64 см2

Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.

Решение

V = abca = 6, b = 4, c = 3V = 6 × 4 × 3 = 72 см3.

Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3

Задача 6. Объем прямоугольного параллелепипеда составляет 200 см3. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см

Решение

V = abcV = 200, a = 10, b = 5, c = x200 = 10 × 5 × x200 = 50xx = 4

Ответ: высота прямоугольного параллелепипеда равна 4 см.

Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га

Решение

Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.

Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.

Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза

4 × 3 = 12 га

Ответ: пшеницей засеяно 12 га.

Задача 8. Длина зернохранилища 42 м, ширина составляет длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.

Решение

a — длинаb — ширинаc — высота

a = 42 мb = мc = 42 × 0,1 = 4,2 м

Определим объем зернохранилища:

V = abc = 42 × 30 × 4,2 = 5292 м3

Определите сколько тонн зерна вмещает зернохранилище:

5292 × 740 = 3916080 кг

Переведём килограммы в тонны:

Ответ: зернохранилище вмещает 3916,08 тонн зерна.

Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.

Решение

Определим сколько литров в минуту вливается через вторую трубу:

25 л/мин × 0,75 = 18,75 л/мин

Определим сколько литров в минуту вливается в бассейн через обе трубы:

25 л/мин + 18,75 л/мин = 43,75 л/мин

Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин

43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л

1 л = 1 дм3

35 525 л = 35 525 дм3

Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:

35 525 дм3 : 1000 дм3 = 35,525 м3

Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:

V = 35,525a = 5.8b = 3.5c = x

35,525 = 5,8 × 3,5 × x35,525 = 20,3 × xx = 1,75 м

с = 1,75

Ответ: высота (глубина) бассейна составляет 1,75 м.

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Основные различия между площадью и периметром

Существенные различия между площадью и периметром подробно представлены в следующих пунктах:

Площадь описывается как измерение поверхности объекта. Периметр относится к контуру, который окружает замкнутую фигуру. .Площадь представляет собой пространство, занимаемое объектом. наоборот, периметр указывает на внешний край или границу формы. Измерение площади выполняется в квадратных единицах, то есть в квадратных километрах, квадратных футах, квадратных дюймах и т. Д. С другой стороны, периметр формы измеряется в линейных единицах, то есть в километрах, дюймах, футах и ​​т. Д.. Поскольку периметр измеряется в линейных единицах, он измеряет только одно измерение, то есть длину объекта

Принимая во внимание, что в случае площади используются два измерения, то есть длина и ширина объекта

Формулы

объект	Площадь	периметр	переменная
Площадь	а ^ 2	4а	где, а = длина стороны
Прямоугольник	л × б	2 (л + б)	где l = длинаб = ширина
Круг	πr ^ 2	2πr = πd	где r = радиус
Треугольник	1/2 чч	а + B + C	где b = основаниеh = высотаa, b, c = длина сторон
Ромб	(PQ) / 2	4а	где а = сторонар и q – диагонали
Параллелограмм	ЬН	2 (а + б)	где b = основаниеh = высотасторона =
трапеция	½ (a + b) × ч	A + B + C + D	где а = базаб = базаh = высотас = сторонад = сторона

Вывод

Изучив вышеприведенные пункты, становится ясно, что эти два математических понятия различны, но вы можете использовать одно, чтобы выяснить другое. В то время как площадь просто означает «покрытое пространство», то есть внутри объекта, периметр относится к «расстоянию вокруг, то есть контуру фигуры». Более того, фигуры с одинаковым периметром могут иметь разную площадь, а фигуры с одинаковой площадью могут иметь разный периметр.

В каких случаях нужны расчеты?

Расчет квадратных метров обязателен, если в проекте установить подвесные потолки. Для наглядности посмотрим, что нужно для гипсокартонных конструкций. Площадь комнаты рассчитывается, чтобы закупить гипсокартон в нужном количестве, а периметр надо знать для покупки пристенного профиля для установки обрешетки. Гипсокартон и профиля берем с запасом примерно 15-20% на обрезку, ведь не всегда можно изобразить на бумаге точный эскиз расположения на потолке гипсокартона или декоративных панелей.

Для заказа натяжного потолка делать расчет квадратуры комнаты требуется, что запланировать будущие траты и проконтролировать фирму-установщика в правильности их расчетов. Фирма, изготавливающая натяжные потолки обычно указывает цену за квадратный метр и плюсует работу по установке. Зная площадь и стоимость квадрата, можно легко определить конечную цену.

Вычислить площадь требуется даже для банальной покраски пола или потолка, чтобы знать, сколько закупать краски

Важно купить нужное количество краски, иначе если не хватит, а краску в магазине колорировали, то можно не угадать с цветом. Примерный расход краски на метр квадратный поверхности указывается на банке

Пример расчета потребности в краске:

Квадратура пола составляет 30 м2

расход краски согласно данным на упаковке – 0,20 кг/м2

30 х 0,2 = 6 кг

Полагается брать краску свыше расчетного количества на 10%.

Поэтому получаем 6 + 10% = 6,6 кг. Это подойдет ведро 7 кг или приближенная расфасовка в зависимости от вида краски.

Периметр и площадь: как одна территория может иметь больше первого, но меньше второго

Периметр и площадь — это два важных термина в геометрии, которые используются для описания размеров плоских фигур. Периметр — это длина границы фигуры, а площадь — это занимаемая фигурой площадь. Часто бывает так, что территория может иметь больший периметр, но меньшую площадь, и наоборот. В этой статье мы рассмотрим примеры таких случаев и объясним, почему это происходит.

Примеры

Пример № 1: территория с большим периметром, но маленькой площадью

На рисунке выше показана территория с большим периметром, но маленькой площадью. Это нерегулярный многоугольник, состоящий из 8 сторон. Чтобы вычислить его периметр, необходимо сложить длины всех его сторон. В данном случае периметр равен 28. Однако вычислить площадь этой территории гораздо сложнее, чем периметр, потому что она не имеет регулярной формы.

Площадь этой территории можно приблизительно вычислить, разбив ее на меньшие фигуры, такие как треугольники и прямоугольники, и вычислив площадь каждой из них. В этом случае мы можем посчитать площадь этой территории, разбив ее на две части: треугольник и четыре прямоугольника. В этом случае площадь территории будет равна приблизительно 16.

Таким образом, мы видим, что территория может иметь больший периметр, но меньшую площадь.

Пример № 2: территория с маленьким периметром, но большой площадью

На рисунке выше показана территория с маленьким периметром, но большой площадью. Это регулярный многоугольник, состоящий из 12 сторон. Чтобы вычислить его периметр, необходимо сложить длины всех его сторон. В данном случае периметр равен 60.

Площадь этой территории можно вычислить, используя формулу для площади многоугольника, которая зависит от количества сторон и длины каждой из них. В этом случае мы можем посчитать площадь этой территории, используя формулу для площади правильного многоугольника, которая зависит от длины его стороны и количества сторон. В этом случае площадь территории будет равна приблизительно 259.8.

Таким образом, мы видим, что территория может иметь маленький периметр, но большую площадь.

Периметр и площадь — это два важных понятия в геометрии, которые помогают нам определить размеры плоских фигур. Как мы видели на примерах выше, территория может иметь больший периметр, но меньшую площадь, и наоборот. Это происходит из-за того, что периметр зависит только от длины границы фигуры, а площадь зависит от размеров ее внутренней площади

Поэтому важно понимать разницу между этими двумя понятиями и уметь применять их в решении геометрических задач

Что такое площадь?

В области геометрии площадь относится к пространству, которое покрыто или занято какой-либо плоской формой или объектом. Слово «площадь» происходит от латинского слова «площадь», что означает любой свободный участок земли.

Площадь также означает определенное количество пространства, которое можно удерживать в закрытых границах. Обычно площадь определяется для двухмерных фигур, таких как квадрат и прямоугольник. При этом есть не только двухмерные, но и трехмерные фигуры, площадь которых необходимо выяснить.

Площадь этих трехмерных фигур называется площадью поверхности. Многие фигуры не так просты, как квадрат, прямоугольник или треугольник, в этих случаях площадь этих составных фигур определяется сложением площадей простых фигур, образующих эти составные.

Стандартная единица площади в Международной системе единиц – квадратные метры, записываемые как м2, где m – длина одной стороны объекта. Области простых фигур, таких как круг, квадрат или треугольник, можно найти с помощью хорошо известных общих формул.

В то время как для многоугольников площадь можно определить, разделив их на соответствующие треугольники, а затем добавив площади всех из них. Алгебраически. Площадь считается квадратом соответствующей единицы длины и, следовательно, может быть в квадратных метрах (м2), квадратные сантиметры (см2), квадратные миллиметры (мм2), квадратных километров (км2), квадратные ярды (yd2) или даже квадратных миль (мм2).

Вот некоторые из основных формул, используемых для определения площади:

1. Площадь: а 2
2. Прямоугольник: ab
3. Параллелограмм: bh
4. Трапеция: h / 2 (b₁ + b₂)
5. Круг: πr²
6. Треугольник: ½ bh

В реальной жизни площадь можно рассчитать, чтобы узнать, сколько ковра нужно использовать для покрытия пола, или даже определить, сколько площади нужно покрасить на навесной стене.

Практическое применение площади и периметра

Область применения	Описание
Строительство	При проектировании зданий и сооружений необходимо учитывать периметр и площадь, чтобы определить необходимое количество материалов, например, для строительства ограждений, пола или крыши. Знание площади поможет определить площадь здания и выбрать оптимальную площадь участка.
Ландшафтный дизайн	При оформлении садов, парков и других ландшафтных объектов площадь и периметр используются для определения площади газонов, клумб, определения формы и размеров альпийской горки, зоны отдыха или огорода.
Дизайн интерьера	Площадь помещений помогает спланировать размещение мебели, выбрать оптимальные размеры и форму комнаты, рассчитать количество материала для пола или обоев. Периметр помогает определить длину обоев, плинтусов, мебели и других элементов интерьера.
Инженерные расчеты	В строительстве и инженерных отраслях площадь и периметр применяются при проектировании дорог, тротуаров, трубопроводов, проводов, площадок. Они помогают определить объемы необходимых материалов и вычислить нагрузки на конструкции.
Торговля и розничная торговля	Площадь помещений, витрин и торговой площади имеет ценность в коммерческом плане. Знание площади и периметра помогает определить стоимость аренды и пространства для размещения товаров или рекламных материалов.
Сельское хозяйство	При размещении полей и огородов площадь и периметр используются для расчета необходимого количества семян, удобрений, агрегатов и прогнозирования урожайности хозяйства.

Все эти примеры демонстрируют практическую значимость понятий площади и периметра. Они помогают определить размеры объектов, рассчитать требуемые ресурсы, спланировать пространство и сделать более обоснованные решения.

Площадь против периметра — разница и сравнение

В геометрии площадь — это двумерное пространство или область, занимаемая замкнутой фигурой, а периметр — это расстояние вокруг замкнутой фигуры, то есть длина границы. Например, площадь может быть использована для расчета размера ковра, чтобы покрыть весь пол комнаты. Периметр может быть использован для расчета длины забора, необходимого для окружения двора или сада. Две фигуры могут иметь одинаковый периметр, но разные области или могут иметь одинаковую площадь, но разные периметры.

Сравнительная таблица

Площадь	периметр
Определение	Пространство или область занята замкнутой фигурой.	Расстояние вокруг закрытой фигуры.
измерение	Квадратная единица. (Кв) Измеряет два измерения, например, 24 дюйма или 24 дюйма в квадрате	Линейный блок Измеряет одно измерение, например, 24 дюйма или 24 дюйма
использование	Например, чтобы ковер на всю комнату	Например поставить забор вокруг сада
Площадь	s², где s — длина одной стороны квадрата.	4s, где s — длина одной стороны квадрата.
Прямоугольник	lw, где l и w — длина и ширина прямоугольника.	2l + 2w, где l и w — длина и ширина прямоугольника.
Треугольник	Площадь корень (s * (sa) (sb) (sc)), где s — половина периметра, a, b и c — длины сторон. ИЛИ ½ * ab * sin (C), где a и b — любые две стороны, а C — угол между ними. ИЛИ ½ * bh, где b — основание, а h — высота	a + b + c, где a, b и c — длины сторон треугольника.
Ромб	Произведение диагоналей / 2	4 * л
трапеция	(А + б) / 2	Сумма всех сторон
Параллелограмм	Длина (л) * высота (ч)	2 * (длина (л) + ширина (б))
Круг	πr², где r — радиус круга.	2πr, где r — радиус

• 1 Измерение и Единицы
• 2 формулы для расчета площади и периметра
• 3 Нерегулярных Объекта
• 4 Ссылки

Площадь каждого рисунка — область красного цвета. Периметр — это черная линия, которая образует границу.

Измерения и Единицы

Площадь представляет собой двумерную область; Таким образом, единица измерения площади — «квадратные единицы». например, 24 дюйма в квадрате или 20 сантиметров в квадрате. Это написано как 20 см 2 .

Мы используем линейные единицы измерения при измерении периметра. Линейные единицы измеряют одно измерение, длину.

Формулы для расчета площади и периметра

Шпаргалка математических формул для расчета площади и периметра для различных геометрических фигур, включая круг, квадрат, треугольник, прямоугольник, равносторонние многоугольники, правильные многоугольники и общие многоугольники.

Нерегулярные объекты

Неправильная форма имеет стороны разной длины. Вычисление площади на этих фигурах включает в себя разбиение фигуры на общие фигуры, такие как квадраты, прямоугольники, треугольники и круги. Это потому, что все эти фигуры имеют заданные формулы для расчета их площади. Возможность видеть фигуры внутри фигуры является ключом к вычислению площади неправильных фигур. После нахождения области каждой фигуры добавьте их, чтобы получить общую площадь. В случае периметра нерегулярного объекта просто измерьте длину каждой стороны и сложите их.

Площадь и Ромб

Квадрат против Ромба В геометрии вы, возможно, узнали о квадратах и ​​ромбе. Это две формы, которые имеют своеобразные сходства, потому что они попадают под одно и то же семейство параллелограммов или четырехугольников. Но прежде чем различать два, лучше всего знать, что такое параллелограмм. Параллельнограмма

Площадь и площадь поверхности

Область против поверхности. Математика имеет способы заставить нас думать, переосмысливать и делать это снова и снова. Как будто математика не слишком запутывает, вызванная ее формулами, операциями и выводами — люди могут также путаться с определениями, особенно с аналогичными терминами. Большинство из нас знают, что геометрия — это

Объем и площадь

Объем против области Обычные люди часто слышат объем и площадь терминов во многих настройках. Пусть это будет дома, в школе или в сообществе, эти слова почти всегда широко используются. Однако в техническом смысле люди часто путают эти термины и добавляют к путанице, каждое определение этого термина иногда может

Свойства прямоугольника

Рассмотрим чем отличается прямоугольник от других фигур.

1. В прямоугольнике противоположные стороны равны.

2. Уровни между собой и имеют 90 градусов все углы прямоугольника.

3. Диагонали прямоугольника равны и в точке пересечения делятся пополам.

4. Диагонали треугольника делят его на два одинаковых треугольника.

Таким образом, если в параллелограмме все углы ровны или один прямой, или одинаковые диагонали то это прямоугольник. Что касается четырехугольников, то среди них прямоугольниками будут только те, у которых все углы равны или хотя бы три прямые. Биссектриса угла прямоугольника отсекает от него равнобедренный треугольник.

Основными геометрическими характеристиками прямоугольника является периметр и площадь.

Обозначения

Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу

S = a2

где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.

Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см2. Это обозначение заменяет словосочетание «квадратный сантиметр».

Например, вычислим площадь квадрат со стороной 2 см.

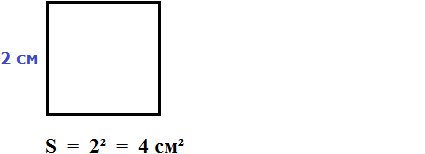
Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:

Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м2. Это обозначение заменяет словосочетание «квадратный метр».

Вычислим площадь квадрата со стороной 3 метра

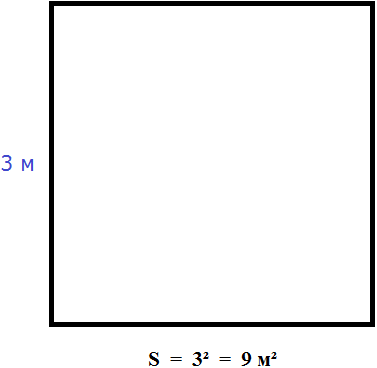
Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:

Аналогичные обозначения используются при вычислении площади прямоугольника. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:

S = a × b

Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см2, м2, км2. Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.

Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см

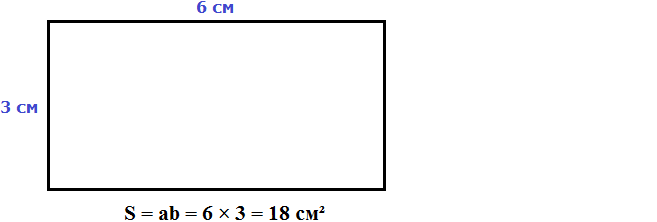
Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:

В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).

Что такое периметр и площадь

Периметр – это геометрический термин, который часто встречается в задачах. Чтобы понять, что такое периметр, следует нарисовать произвольный многоугольник и вооружиться линейкой. В переводе с греческого языка этот термин обозначает «измеряю вокруг».

Периметр обозначается латинской буквой P. Его можно измерить в сантиметрах, миллиметрах, метрах или дециметрах. Чтобы узнать периметр, следует измерить длину всех сторон многоугольника. Полученные значения нужно сложить. Итоговая сумма и станет ответом на вопрос: «Чему равен периметр многоугольника».

Периметр – это длина линий, которые ограничивают замкнутую фигуру (квадрат, прямоугольник, треугольник и др.).

Например, перед вами многоугольник со сторонами 10, 12, 13 и 11 см. Складываем вышеназванные числа (10+12+13+11) и получаем сумму 46. Это и есть периметр многоугольника.

Для удобства вычисления периметра в геометрии существует ряд формул. Каждая формула соответствует определенной фигуре.

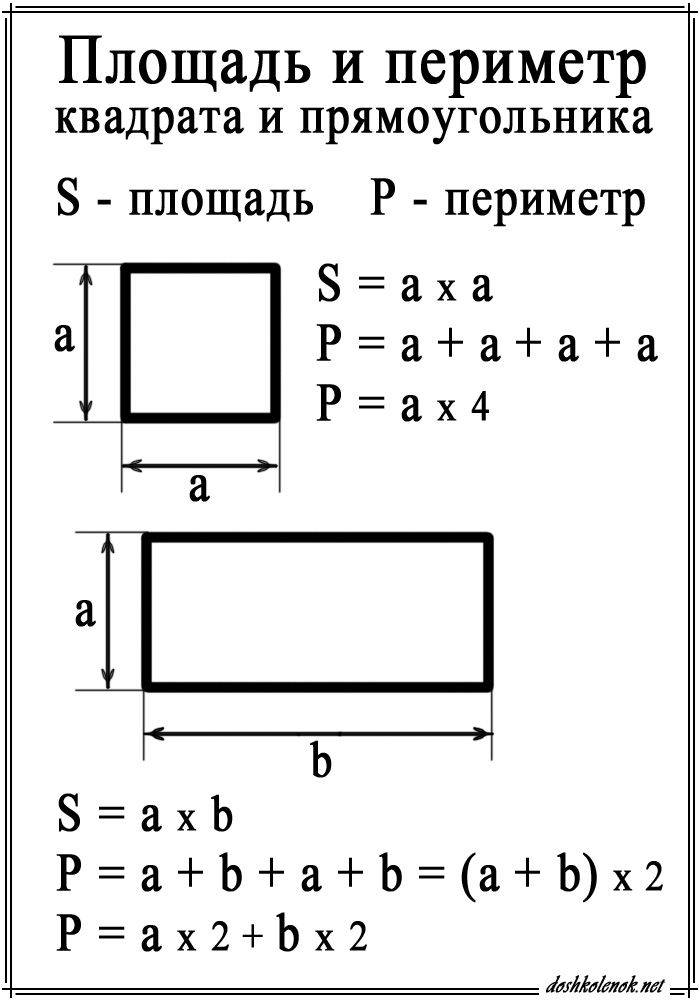
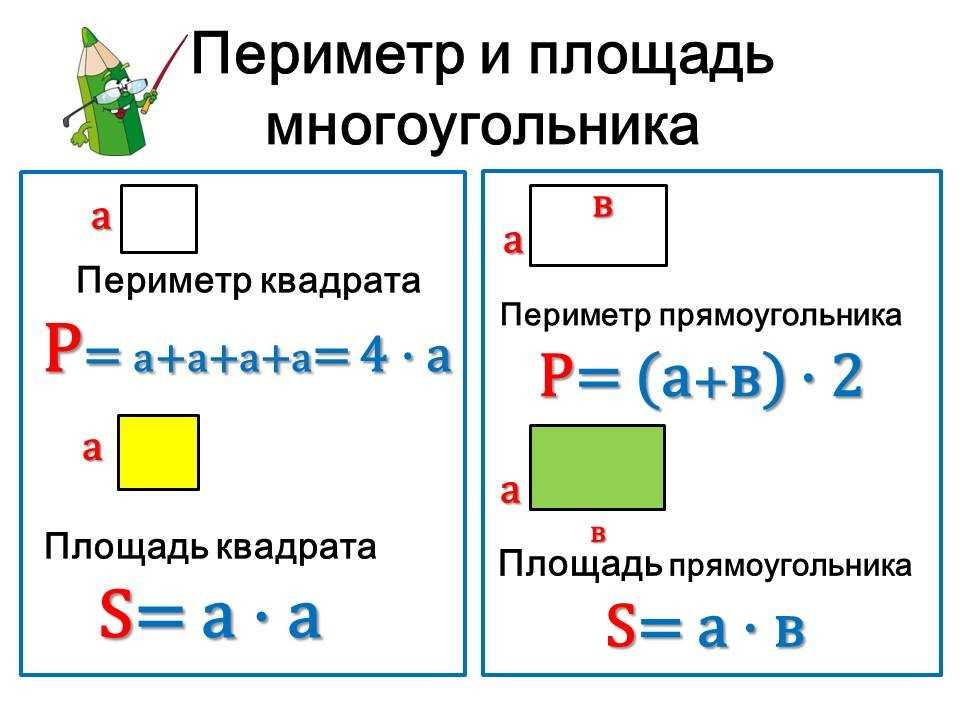
Периметр и площадь квадрата

Это сумма его четырех сторон. Как мы знаем, все стороны квадрата имеют равный размер. Поэтому мы можем узнать периметр квадрата, умножив длину его стороны на четыре:

• P= a*4
• P= a+a+a+a

Например, перед нами квадрат со стороной 10 см:

• P= 10*4
• P=40

Ответ: 40 см

• P= 10+10+10+10
• P=40

Ответ: 40 см

Чтобы разобраться, что такое периметр и площадь, следует уяснить, что периметр вычисляет длину контура фигуры, а площадь – размер всей ее поверхности.

Чтобы узнать площадь квадрата, необходимо воспользоваться простой формулой:

• S= a*a
• S=a2

S – это площадь, а – сторона квадрата.

Например, в задаче указано, что длина стороны квадрата составляет 10см.

• S=10*10
• S= 100см2

Ответ: 100см2

Периметр и площадь прямоугольника

Стороны прямоугольника, находящиеся друг напротив друга и имеющие одинаковую длину, называются противолежащими. Это длина и ширина, они условно обозначаются латинскими буквами a и b. Формула для вычисления периметра прямоугольника выглядит так:

P= (a+b)*2

Используя эту формулу, мы сначала находим сумму ширины и длины, а затем умножаем ее на два. Например, перед нами прямоугольник, имеющий длину 6 см и ширину 2 см:

• P= (6+2) * 2
• P= 16

Ответ: 16 см

Чтобы узнать площадь прямоугольника, следует длину умножить на ширину. Формула выглядит так:

S= a*b

Например, в условиях задачи сказано, что прямоугольник имеет длину 5 см и ширину 2см. Меняем буквы a и b на указанные числа:

1. S= 5*2
2. S=10см2

Ответ: 10 см2

Периметр круга (длина окружности)

Каждый круг имеет центр. Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.

Чтобы найти периметр круга, следует вычислить длину его окружности. Существует формула для нахождения длины окружности:

• L = 2πr
• L= 2πd

L – длина окружности

π – это число «пи», математическая константа. Она равна отношению длины окружности к длине ее диаметра. Древнее название числа «пи» – лудольфово число. Это число иррационально, его десятичное представление после точки никогда не заканчивается.

π = 3.141 592 653 589 793 238 462 643 383 279 502

Для удобства вычислений обычно используют значение 3.14

R – это радиус окружности

D – Диаметр окружности

Итак, чтобы определить периметр круга, надо найти произведение радиуса и 2π. Если в задаче указан диаметр, то

Например, перед нами круг с радиусом 3 см. Найдем его периметр:

• L= 2*3,14*3
• L=6π
• L=6*3.14
• L = 18.84 см
• Pк= 18,84 см

Ответ: 18.84 см

Отличие периметра от площади

Площадь – это размер поверхности фигуры, а периметр – это сумма ее границ. Площадь всегда измеряется в квадратных единицах (см2, м2, мм2). Периметр измеряется в единицах длины – в сантиметрах, миллиметрах, метрах, дециметрах.

Что такое площадь?

В области геометрии площадь относится к пространству, которое покрыто или занято какой-либо плоской формой или объектом. Слово «площадь» происходит от латинского слова «площадь», что означает любой свободный участок земли.

Площадь также означает определенное количество пространства, которое можно удерживать в закрытых границах. Обычно площадь определяется для двухмерных фигур, таких как квадрат и прямоугольник. При этом есть не только двухмерные, но и трехмерные фигуры, площадь которых необходимо выяснить.

Площадь этих трехмерных фигур называется площадью поверхности. Многие фигуры не так просты, как квадрат, прямоугольник или треугольник, в этих случаях площадь этих составных фигур определяется сложением площадей простых фигур, образующих эти составные.

Стандартная единица площади в Международной системе единиц – квадратные метры, записываемые как м2, где m – длина одной стороны объекта. Области простых фигур, таких как круг, квадрат или треугольник, можно найти с помощью хорошо известных общих формул.

В то время как для многоугольников площадь можно определить, разделив их на соответствующие треугольники, а затем добавив площади всех из них. Алгебраически. Площадь считается квадратом соответствующей единицы длины и, следовательно, может быть в квадратных метрах (м2), квадратные сантиметры (см2), квадратные миллиметры (мм2), квадратных километров (км2), квадратные ярды (yd2) или даже квадратных миль (мм2).

Вот некоторые из основных формул, используемых для определения площади:

В реальной жизни площадь можно рассчитать, чтобы узнать, сколько ковра нужно использовать для покрытия пола, или даже определить, сколько площади нужно нарисовать на ненесущей стене.

Многоугольник

Правильный полигон – это выпуклая фигура на плоскости, которая имеет равные стороны и равные углы. В зависимости от количества сторон многоугольники имеют собственные названия:

• – пентагон;
• – гексагон;
• восемь – октагон;
• двенадцать – додекагон.

И так далее. Геометры шутят, что круг – это многоугольник с бесконечным количеством углов. Наш калькулятор запрограммирован на определение периметров и площадей только правильных многоугольников. Он использует общие формулы для всех правильных полигонов. Для вычисления периметра используется формула:

где n – количество сторон многоугольника, a – длина стороны.

Для определения площади используется выражение:

S = n/4 × a 2 × ctg(pi/n).

Подставляя соответствующее n, мы можем подобрать формулу для любого правильного многоугольника, к которым также относятся равносторонний треугольник и квадрат.

Многоугольники имеют большое распространение в реальной жизни. Так форму пятиугольника имеет здание министерства обороны США – Пентагон, гексагона – пчелиные соты или кристаллы снежинки, октагона – дорожные знаки. Кроме того, многие простейшие, например радиолярии, имеют форму правильных полигонов.

В заключение

Не стоит скрупулезно обмерять и высчитывать все значения. В любом случае будет погрешность около 5%, но сколь либо серьезно это значение не влияет на расчеты

Можно не брать во внимание небольшие скругления углов. Если надо рассчитать площадь стен для закупки отделочных материалов, то действуем по первому примеру с правильным прямоугольником, вычитая площадь окон и дверей

В наших домах стандартная высота потолков может разниться в каждом из углов, поэтому берем большее значение с учетом обрезки. Пусть лучше будет небольшой запас, чем потом думать, как выйти из ситуации. Удачи вам в ремонте!

Пери́метр (др. -греч. περίμετρον – окружность, др. -греч. περιμετρέο – измеряю вокруг) – общая длина границы фигуры (чаще всего на плоскости). Имеет ту же размерность величин, что и длина. Иногда периметром называют границу геометрической фигуры.

Пло́щадь – численная характеристика двумерной (плоской или искривлённой) геометрической фигуры , неформально говоря, показывающая размер этой фигуры. Исторически вычисление площади называлось квадратурой. Фигура, имеющая площадь, называется квадрируемой. Конкретное значение площади для простых фигур однозначно вытекает из предъявляемых к этому понятию практически важных требований (см. ниже). Фигуры с одинаковой площадью называются равновеликими.

Периметр фигуры обладает только одним параметром – протяжённостью, или длиной, выраженной в единицах длины: метр, ярд, аршин, локоть. Или производных от них: километр, сантиметр, дециметр.

Площадь фигуры обладает двумя параметрами – например, длиной и шириной, или радиусом и коэффициентом Пи, в зависимости от формы. Величина площади выражается в единицах в квадрате: квадратных метрах, гектарах, квадратных милях