Чем отличается луч от прямой

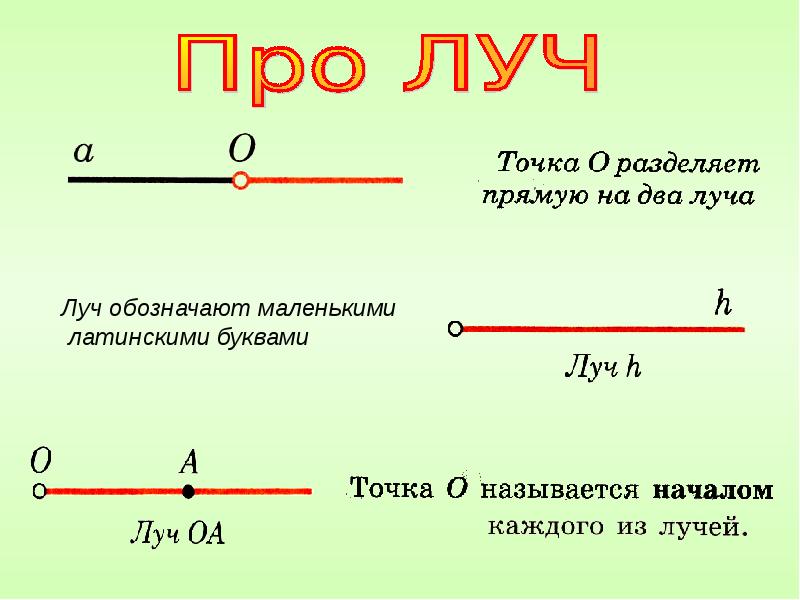
Как обозначаются лучи

Продолжим вспоминать, что представляет собой луч и как его обозначить.

Вариантов обозначения несколько:

Начертим в тетрадке прямую, обозначим точку начала луча. И присвоим ей имя. Например, пусть это будет луч «С». Первая точка – это начало луча, второй точки, как вы уже вспомнили, не существует. Это классическая схема обозначения лучей.
Второй вариант поинтереснее: луч можно обозначить несколькими буквами. Например, на одном луче может быть 2 буквы. Первая – это начало луча, пусть это будет буква А, а вторая может располагаться с определенным шагом. Допустим, на отрезке длиной 10 см начало луча обозначено буквой А, а на расстоянии 4 см от начала луча имеется вторая точка, точка В. Тогда луч нужно обозначить, как луч «АВ». Чтобы было понятнее, читать можно так: вторая точка В – это точка, через которую проходит луч.
Лучи еще можно обозначить и третьим способом, когда начальная точка будет находиться не в начале луча, а с небольшим отступлением. Например, чертим прямую длиной 10 см, отступаем от левого края 1 см, ставим точку – это будет начало луча. Обозначаем, например, буквой О. Посередине луча точку не ставим, но обозначаем эту часть луча буквой К. В данном случае буква О, будет началом этого луча, он исходит из этой точки. Читается луч так: «ОК», он является полупрямым.

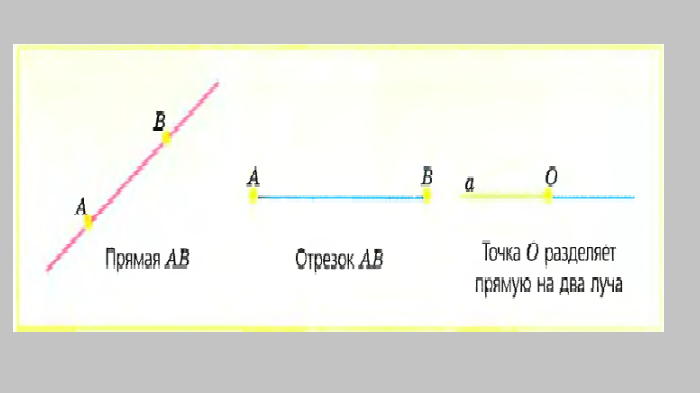
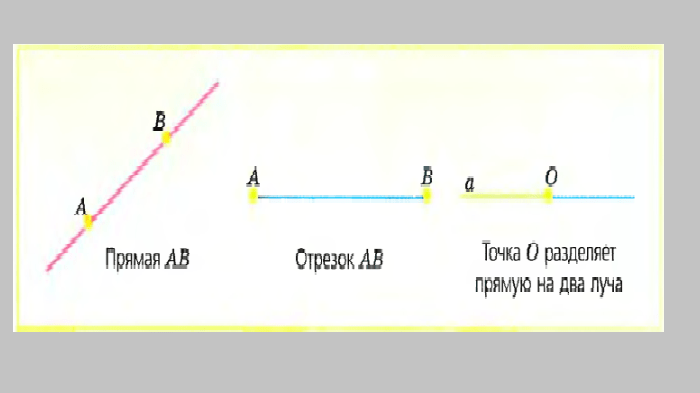
Луч как граница

Луч – это одна из геометрических фигур в математике, которая выглядит как бесконечная прямая линия с точкой начала, называемой началом луча.

Луч может служить границей для областей на плоскости. Например, если мы хотим отделить часть плоскости слева от начала координат, мы можем провести луч, и все, что находится справа от этого луча, будет отнесено к одной области, а все, что находится слева от луча – к другой.

Более того, луч может служить границей для множеств точек на плоскости. Например, если мы хотим отделить все точки, лежащие в верхней полуплоскости, мы можем провести луч начинающийся в начале координат, и все точки, находящиеся выше этого луча, будут принадлежать этому множеству, а все точки ниже луча – другому.

Когда использовать прямую луч и отрезок?

Отрезок — это часть прямой между двумя точками. Он имеет начало и конец, т.е. конечные точки. Отрезок обладает определенной длиной, которая вычисляется как расстояние между его конечными точками. Отрезок может быть использован, когда необходимо задать конкретное расстояние между точками или обозначить границу между двумя объектами.

Прямая же является бесконечной линией, не имеющей начала и конца. Она продолжается в бесконечность в обоих направлениях

Прямая используется, когда не требуется указывать конкретные границы и точки, а важно описать направление или общее расположение объектов

Луч — это часть прямой, имеющая начало, но не имеющая конца. Она распространяется от начальной точки в определенном направлении. Луч используется, когда необходимо указать направление или показать, что объект расположен в определенной части пространства.

Таким образом, использование отрезка, прямой или луча зависит от задачи, которую необходимо решить в геометрии. Отрезок используется для определения конкретного расстояния или границы, прямая — для указания направления или общего расположения, а луч — для показа направления или местоположения в пространстве.

Применение прямого луча

Расстояние: Прямой луч может быть использован для измерения расстояния между двумя точками на прямой. Для этого необходимо отложить на луче от точки измерения нужное расстояние и удалиться в противоположном направлении до встречи с прямой или другим объектом.
Направление: Прямой луч указывает на направление движения или расположения объекта. Например, при ориентировании на карте можно использовать прямой луч для указания вектора движения от одной точки к другой.
Отрезать: Прямой луч может быть использован для отрезания или разделения пространства на две части. Например, чтобы разделить плоскость на два полутора покрытых прямолинейными фигурами, можно провести прямой луч, который будет служить границей разделения.

В целом, применение прямого луча в геометрии позволяет решать множество задач, связанных с измерением расстояний, определением направления и разделением пространства. Этот геометрический объект играет важную роль в понимании и визуализации различных феноменов в геометрии и других областях науки.

Применение отрезка

В геометрии, отрезок используется для определения расстояния между двумя точками. Он является более конкретным понятием, чем прямая или луч, потому что имеет фиксированную длину. Расстояние между двумя точками на плоскости может быть выражено как длина отрезка, соединяющего эти точки.

Отрезок также является важным понятием в физике. Например, вектор скорости может быть представлен в виде отрезка, указывающего направление и величину движения тела. Отрезок также используется в описании других векторных величин, таких как сила, импульс и момент силы.

В отличие от луча, отрезок имеет конечную длину и не простирается до бесконечности. Он имеет точно определенные начало и конец, и может быть визуализирован как отрезок на плоскости или в пространстве.

Отрезок также может быть использован для определения направления в пространстве. Его направление определяется вектором, который начинается в начале отрезка и указывает к его концу. Вектор отрезка позволяет определить перемещение и изменение позиции объекта в пространстве.

Прямая

Прямая может быть задана различными способами, такими как уравнение вида y = kx + b или вектором, направленным вдоль линии. Она не имеет ни начала, ни конца, и бесконечно простирается в обе стороны.

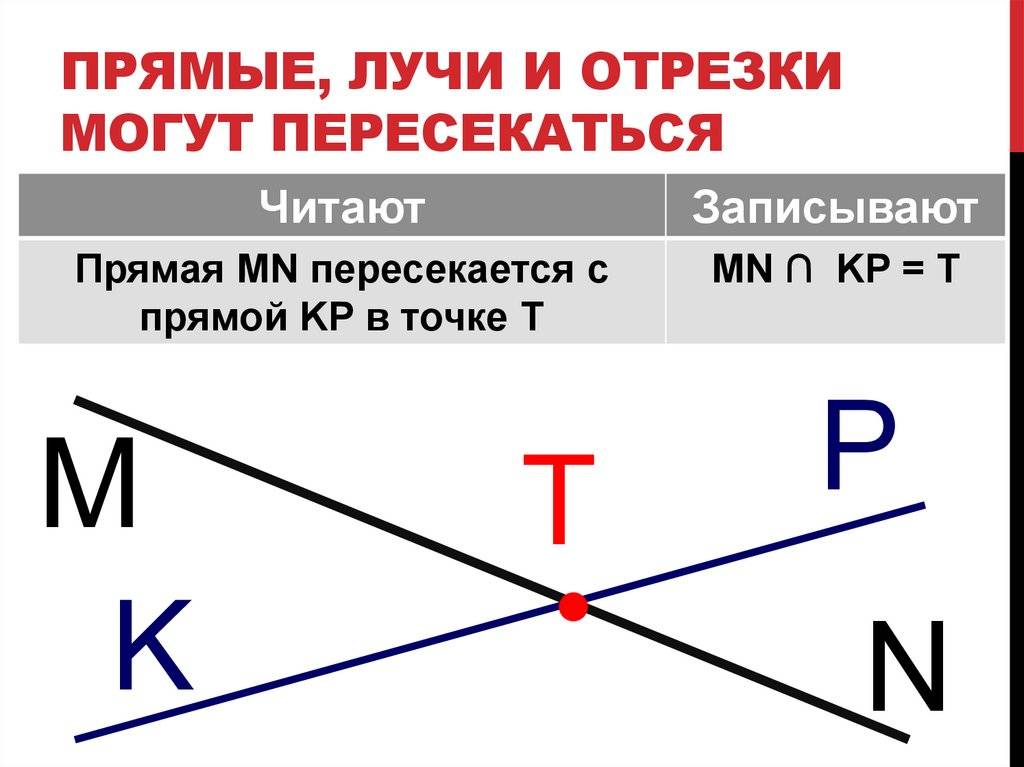
Прямая может пересекаться с другими геометрическими объектами, такими как отрезки, углы или окружности. Она может также быть параллельна другой прямой, иметь общую точку или вступать в пересечение с другими линиями.

В геометрии, прямая используется для построения и изучения различных фигур и форм, а также для решения уравнений и задач в алгебре. Математические законы и теоремы о прямой позволяют нам лучше понять и описать окружающий нас мир.

Прямая является одним из основных строительных блоков геометрии и науки. Она находит применение не только в математике, но и во многих других областях, таких как физика, инженерия и компьютерная графика. Понимание и использоание прямых помогает нам решать практические задачи и находить рациональные решения в различных ситуациях.

Определение прямой

Геометрическое понятие.
Отрезок, содержащийся на плоскости, исключая его начало и конец.
Линия, у которой все точки лежат на одной плоскости и простираются в бесконечность.

Прямая является одной из основных геометрических фигур и часто используется для описания и анализа различных объектов в математике и физике. Прямая может быть определена как набор точек, которые обладают одинаковым направлением и не имеют изгибов или изломов.

Прямая также может быть определена с помощью алгебраических уравнений или геометрических построений. В алгебраической форме прямая может быть описана уравнением вида y = mx + b, где m — коэффициент наклона, а b — свободный член. В геометрическом построении прямая может быть определена как наименьшая длина соединяющая две точки или как кратчайший путь между двумя точками.

Прямая имеет множество свойств и характеристик, таких как наклон, параллельность, перпендикулярность, отношение расстояний и др. Эти свойства широко применяются в различных областях науки и инженерии.

Характеристики прямой

Ниже перечислены основные характеристики прямой:

Наклон: Прямая может быть вертикальной, горизонтальной или наклонной. Вертикальная прямая идет вверх или вниз, горизонтальная прямая идет слева направо, а наклонная прямая идет под углом к вертикали или горизонтали.
Угол наклона: Если прямая наклонная, можно измерить угол наклона относительно горизонтали или вертикали. Угол наклона может быть положительным (прямая идет вверх) или отрицательным (прямая идет вниз).
Уравнение: Каждая прямая может быть описана уравнением. Уравнение прямой выражает связь между координатами точек, лежащих на этой прямой.
Точка пересечения: Две прямые могут пересекаться в одной точке. Эта точка называется точкой пересечения и является решением системы уравнений прямых.
Расстояние: Для прямой можно посчитать расстояние между точками, или от точки до прямой. Расстояние между точками на прямой определяется как абсолютная величина разности их координат.

Какие кривые линии существуют

В геометрии существует множество различных кривых линий, каждая из которых обладает своими уникальными свойствами и характеристиками. Некоторые из наиболее распространенных типов кривых линий включают:

1. Прямая: прямая линия, которая не имеет ни начала, ни конца. Прямая может быть описана как наименее изогнутая линия между двумя точками.

2. Окружность: кривая линия, которая состоит из всех точек, находящихся на одинаковом расстоянии от центра. Окружность имеет радиус, который определяет ее размер, и может быть описана с помощью центра и радиуса.

3. Эллипс: кривая линия, которая похожа на окружность, но имеет два фокуса. Эллипс может быть описан с помощью центра, большей полуоси и меньшей полуоси.

4. Парабола: кривая линия, которая представляет собой симметричное относительно прямой графическое представление квадратичной функции. Парабола имеет одну вершину и две ветви, которые расходятся.

5. Гипербола: кривая линия, которая имеет два фокуса и две ветви. Гипербола состоит из всех точек, для которых разность расстояния до одного фокуса и расстояния до другого фокуса постоянна.

Это только некоторые из различных кривых линий, которые существуют в геометрии. Изучение этих кривых линий помогает понять различные аспекты геометрии и их применение в реальном мире.

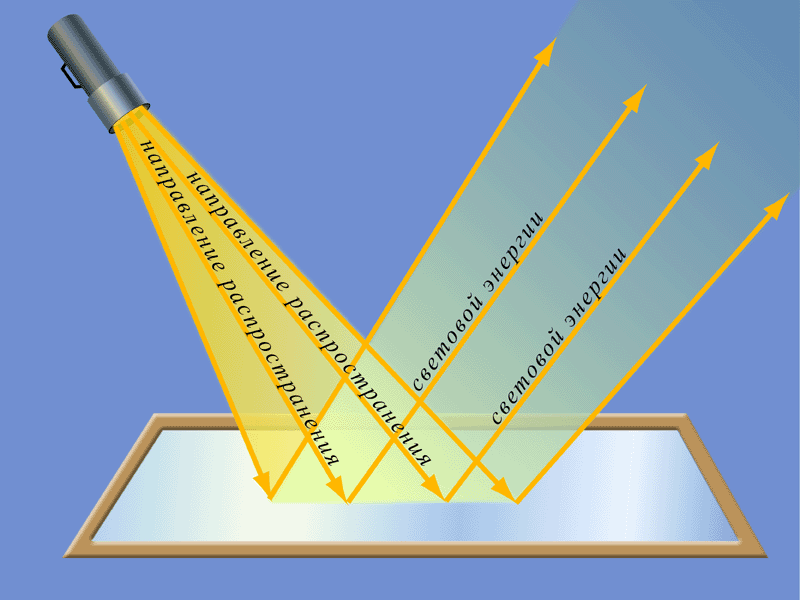
Световой луч

Геометрическая оптика рассматривает понятие светового луча довольно схожим образом. Здесь он тоже будет являться линией, однако она будет использоваться световой энергией. Иначе говоря, световой луч – это небольшой пучок света
.

Как и понятие прямой в геометрии, так и понятие луча в оптике является довольно базовым явлением. Однако, в отличие от геометрического луча, световой не имеет какого-то четкого направления, так как происходит дифракция. Однако, если свет очень большой, то расходимостью принято пренебрегать. В этом случае можно выделить четкое направление.

Эти яхты являются одноместными и используются для гонок. Часто их применяют в качестве обучающего снаряда для детей, однако на нем проводятся и соревнования.

Существуют и другие значения:

Этим словом называются три российских спутника-ретранслятора.
В Удмуртии и Предуралье выходит журнал с таким названием.
Лучом назвали и объединение атомной промышленности.
С таким названием есть часовой завод и обувная фабрика в Минске.
Луч – это псевдоним чувашского писателя, официальное имя которого Григорий Васильевич Васильев.

Все мы когда-то изучали в школе геометрию, но далеко не каждый из нас вспомнит, что представляет собой отрезок. А уж тем более мало кто сможет объяснить понятие лучей, и как они обозначаются. Давайте постараемся в этой статье напомнить себе данные определения и рассмотрим их в математике. Также определим, что такое луч, и чем он отличается от светового. Если вникнуть, то понять будет несложно.

Общая характеристика кривых линий

Одной из основных характеристик кривых линий является их наклон или угол наклона. Наклон определяет, как кривая меняет направление движения в разных ее точках. Если наклон постоянен, то кривая называется прямой. Если наклон меняется, то кривая называется кривой.

Кривые линии также могут быть открытыми или замкнутыми. Открытые кривые линии имеют начальную и конечную точки, между которыми они простираются. Примерами открытых кривых линий являются прямая и ломаная. Замкнутые кривые линии не имеют начальной и конечной точек и образуют замкнутую фигуру. Примерами замкнутых кривых линий являются окружность и эллипс.

Контурная линия — это линия, которая объединяет точки на плоскости. Она может быть прямой, окружностью, эллипсом или другой кривой фигурой. Контурные линии часто используются для описания форм и контуров объектов.

Все кривые линии имеют свои уникальные свойства и характеристики, которые определяют их форму и поведение. Изучение этих свойств и характеристик позволяет лучше понять и описать кривые линии и использовать их в различных областях, таких как геометрия, физика, инженерия и искусство.

Тип кривой	Характеристики
Прямая	Наклон не меняется
Ломаная	Составлена из отрезков прямых линий
Окружность	Все точки равноудалены от центра
Эллипс	Составлен из двух фокусов и плоской кривой линии

Многоугольник — это замкнутая ломанная линия

Стороны многоугольника (помогут запомнить выражения: “пойти на все четыре стороны”, “бежать в сторону дома”, “с какой стороны стола сядешь?”) — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.

Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.

Обозначается многоугольник перечислением всех его вершин.

сторона EF и сторона FA являются смежными

Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599

Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т.д.

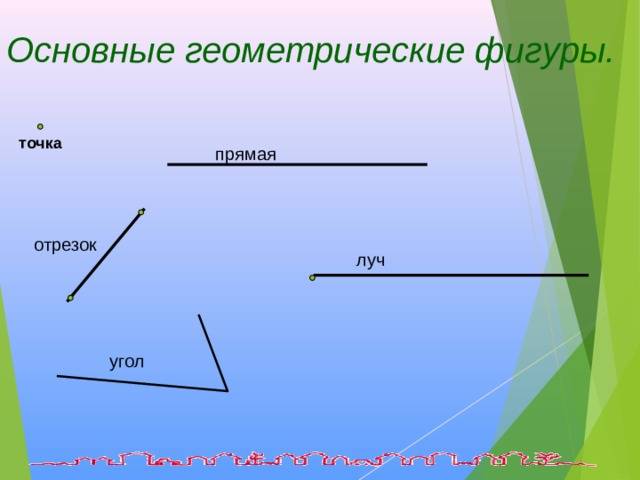
Точка и прямая являются основными геометрическими фигурами на плоскости.

Древнегреческий учёный Евклид говорил: «точка» – это то, что не имеет частей». Слово «точка» в переводе с латинского языка означает результат мгновенного касания, укол. Точка является основой для построения любой геометрической фигуры.

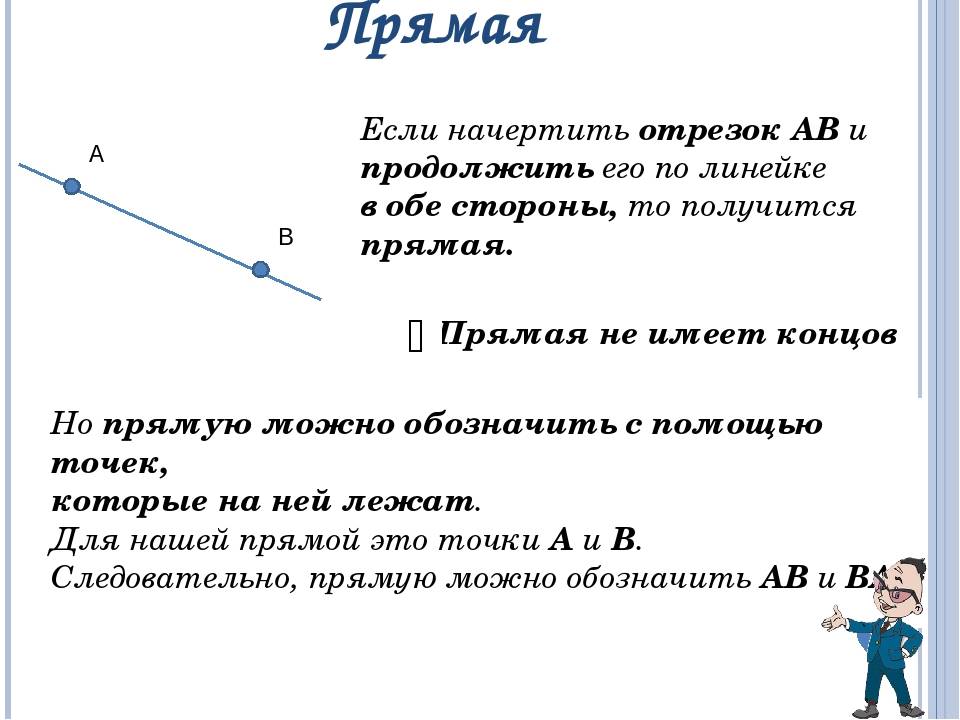
Прямая линия или просто прямая – это линия, вдоль которой расстояние между двумя точками является кратчайшим. Прямая линия бесконечна, и изобразить всю прямую и измерить её невозможно.

Точки обозначают заглавными латинскими буквами А, В, С, D, Е и др., а прямые теми же буквами, но строчными а, b, c, d, e и др. Прямую можно обозначить и двумя буквами, соответствующими точкам, лежащим на ней. Например, прямую a можно обозначить АВ.

Можно сказать, что точки АВ лежат на прямой а или принадлежат прямой а. А можно сказать, что прямая а проходит через точки А и В.

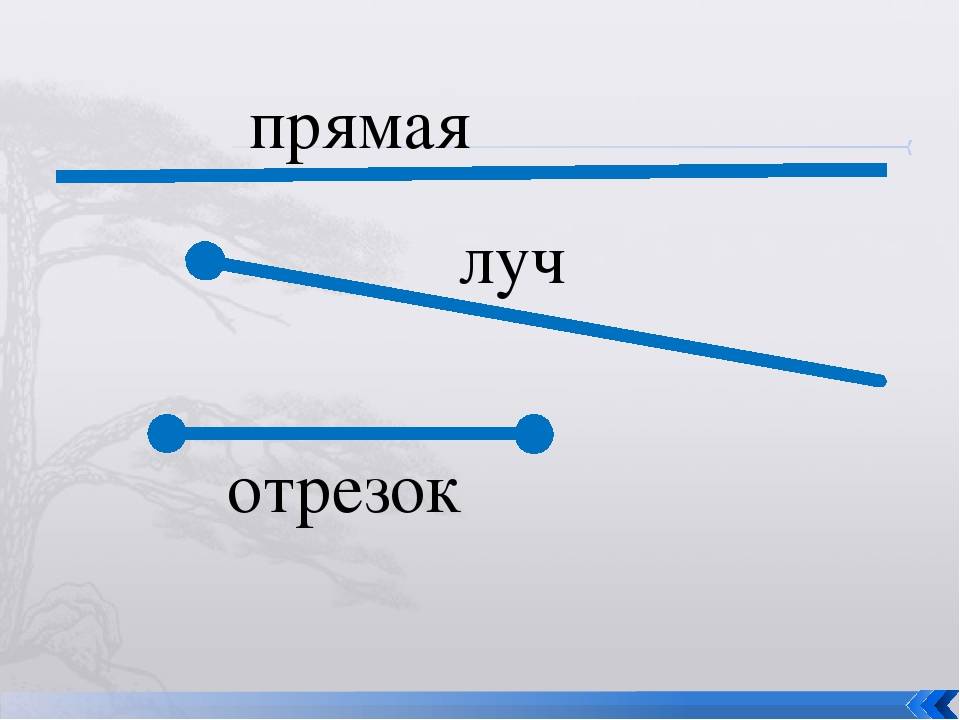
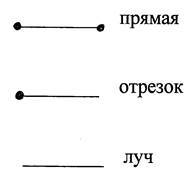
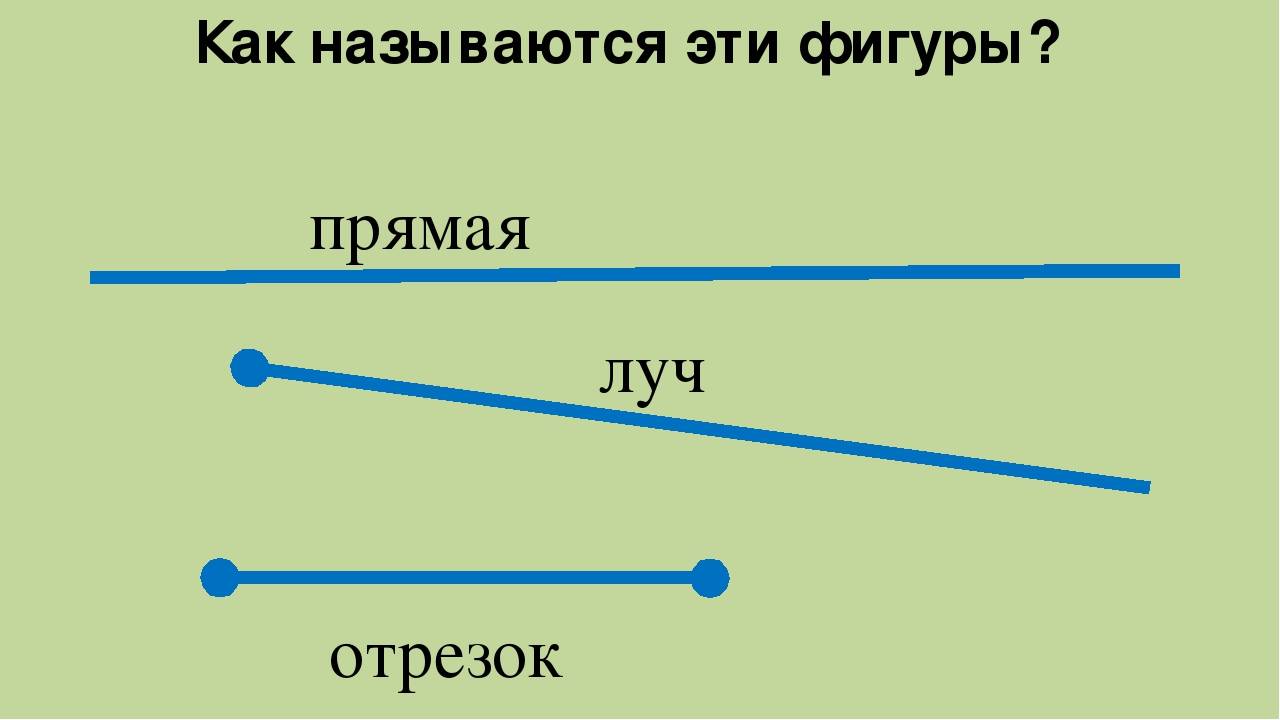
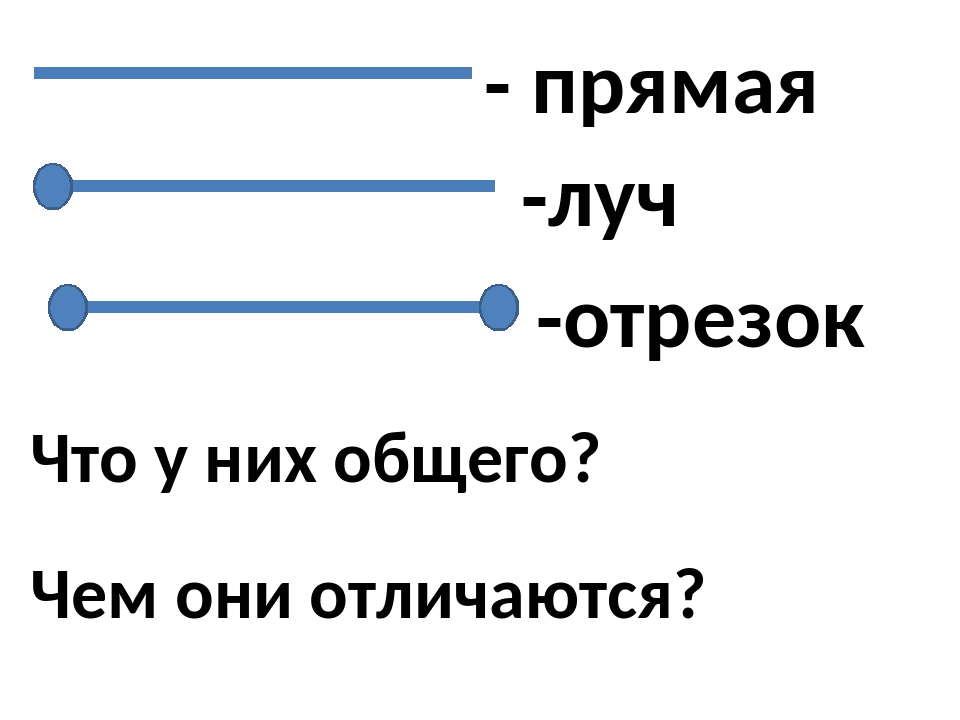
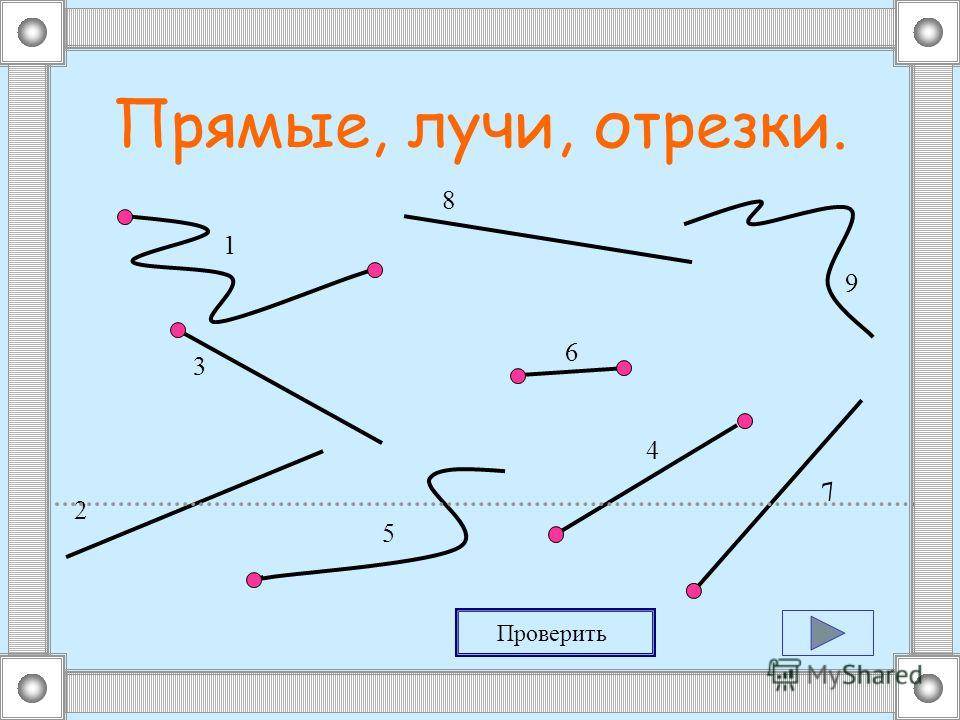
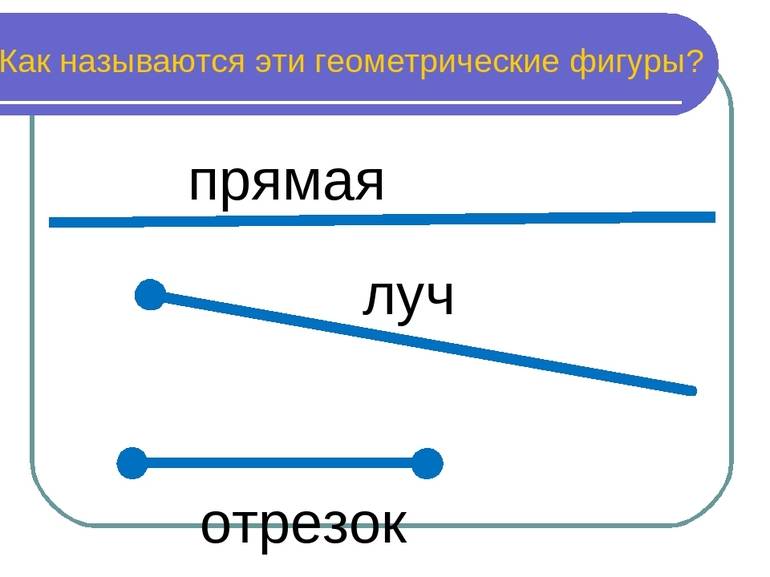
Простейшие геометрические фигуры на плоскости – это отрезок, луч, ломаная линия.

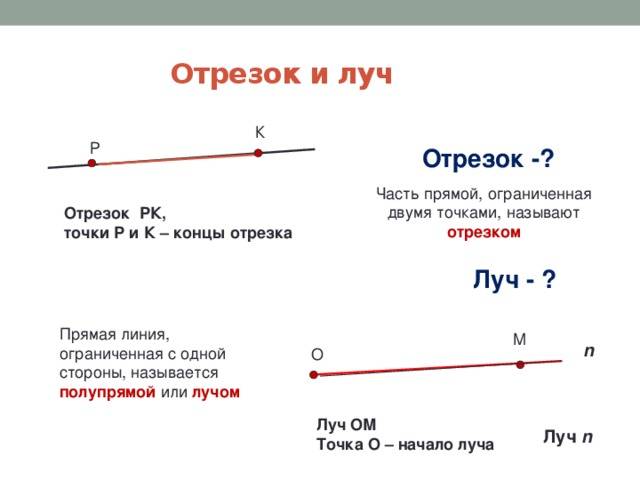
Отрезок – это часть прямой, которая состоит из всех точек этой прямой, ограниченных двумя выбранными точками. Эти точки – концы отрезка. Отрезок обозначается указанием его концов.

Луч или полупрямая – это часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной её точки. Эта точка называется начальной точкой полупрямой или началом луча. Луч имеет точку начала, но не имеет конца.

Полупрямые или лучи обозначаются двумя строчными латинскими буквами: начальной и любой другой буквой, соответствующей точке, принадлежащей полупрямой. При этом начальная точка ставится на первом месте.

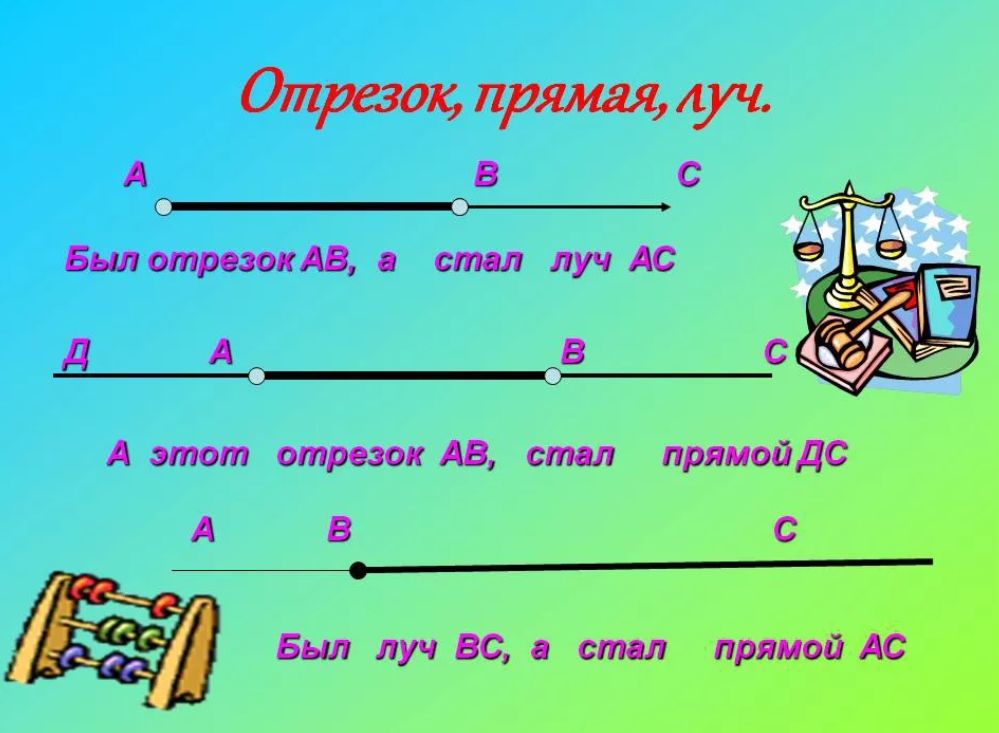
Получается, что прямая бесконечна: у неё нет ни начала, ни конца; у луча есть только начало, но нет конца, а отрезок имеет начало и конец. Поэтому только отрезок мы можем измерить.

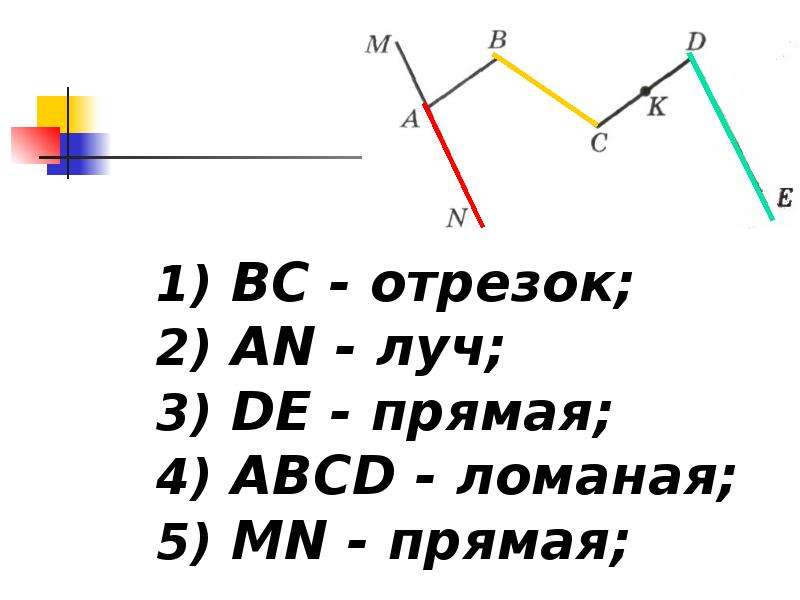
Несколько отрезков, которые последовательно соединены между собой так, что имеющие одну общуюточкуотрезки (соседние) располагаются не на одной прямой, представляют собой ломаную линию.

Ломаная линия может быть замкнутой и незамкнутой. Если конец последнего отрезка совпадает с началом первого, перед нами замкнутая ломаная линия, если же нет – незамкнутая.

сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Наряду с такими понятиями как точка, отрезок, прямая, в геометрии существует и еще одно понятие. Оно имеет название луч. Луч – это часть прямой, ограниченная с одной стороны точкой, а с другой стороны – бесконечная, т.е. ни чем не ограниченная.

Можно провести аналогию с природой. Например, луч света, который мы можем направить с земли в космос. С одной стороны он ограничен, а с другой стороны – нет. Каждый луч имеет одну крайнюю точку, в которой он начинается. Она называется началом луча
.

Если взять произвольную прямую a
, и отметим на ней некоторую точку О
, то эта точка разобьет нашу прямую на две части. Каждая из которых будем лучом. Точка О будет принадлежать каждому из этих лучей. Точка О будет в данном случае началом этих двух лучей.

Луч обычно обозначают одной латинской буквой. На рисунке ниже представлен луч k
.

Также можно обозначать луч двумя большими латинским буквами. При этом первая из них – это точка, в которой лежит начало луча. Вторая – это точка которая принадлежит лучу или другими словами – через которую луч проходит.

На рисунке представлен луч ОС.

Еще одним способом обозначения луча, является указание начальной точки луча и прямой, которой этот луч принадлежит. Например, на рисунке ниже представлен луч Оk.

Иногда говорят, что луч исходит из точки О. Это значит, что точка О является началом луча. Лучи еще иногда называют полупрямыми
.

Как определить направление луча

Луч — это прямая, исходящая из определенной точки и не имеющая начала и конца. В математике луч используется для указания направления, перемещения и расположения объектов относительно друг друга.

Направление луча можно определить по двум основным признакам — начальной точке и углу. Начальная точка указывает на место, где луч начинается, а угол показывает направление, в котором он движется.

Если луч начинается от точки А и направлен вверх, то его направление будет указано как «вверх». Если же луч начинается от точки А и направлен вниз, то его направление будет указано как «вниз». Аналогично, если луч начинается от точки А и направлен влево или вправо, то его направление будет соответственно «влево» или «вправо».

Изучение направления луча помогает ребенку развивать навыки ориентирования в пространстве и улучшать геометрическую интуицию. Эти навыки помогают ребенку в будущем решать более сложные задачи в области математики и физики.

Сочетания лучей и отрезков

В математике есть возможность комбинировать лучи и отрезки, чтобы создавать более сложные геометрические фигуры.

Луч – это бесконечная прямая, которая имеет начальную точку и простирается в бесконечность в определенном направлении. Отрезок – это часть прямой между двумя точками.

Одно из самых простых сочетаний лучей и отрезков – лучевой отрезок. Лучевой отрезок создается путем рисования отрезка на луче, начиная с его начальной точки и заканчивая в любой другой точке луча.

Сочетание луча и отрезка может быть полезно при решении геометрических задач, таких как определение длины отрезка на луче или нахождение точек пересечения двух лучей или отрезков.

Луч	Отрезок	Лучевой отрезок

Например, если мы имеем луч AB и отрезок CD, то мы можем построить лучевой отрезок AC, начинающийся в точке A и проходящий через точку C на луче AB.

Сочетание лучей и отрезков – это один из способов расширить понимание геометрических фигур и решить сложные задачи, которые требуют комбинации различных элементов.

Определение отрезка

Отрезок не имеет длины, а только конечную протяженность. Он изображается на графике в виде сегмента прямой, заключенного между двумя точками. В обозначениях отрезка используют две буквы с чертой сверху, например AB – обозначение отрезка с концами в точках A и B.

Длина отрезка вычисляется с помощью формулы длины отрезка AB = √((x2 — x1)² + (y2 — y1)²), где (x1, y1) и (x2, y2) – координаты точек A и B соответственно.

Пример	Описание
AB	Отрезок с концами в точках A и B
BC	Отрезок с концами в точках B и C
CD	Отрезок с концами в точках C и D

Отрезок отличается от прямого луча тем, что прямой луч имеет только одну точку начала и бесконечно продолжается в одном направлении, в то время как отрезок имеет две конечные точки и имеет ограниченную протяженность.

Как определить отрезок?

Чтобы определить отрезок, нужно:

Найти координаты начальной точки отрезка. Начальная точка обозначается как A(x1, y1).
Найти координаты конечной точки отрезка. Конечная точка обозначается как B(x2, y2).
Составить уравнения прямых, проходящих через начальную и конечную точки отрезка. Уравнения прямых имеют вид y = kx + b, где k — угловой коэффициент, b — свободный член.
Решить систему уравнений для нахождения коэффициентов k и b.
Подставить найденные значения углового коэффициента и свободного члена в уравнение и проверить, что оно соответствует координатам начальной и конечной точек отрезка.

Пример:

Для отрезка AB с начальной точкой A(1, 2) и конечной точкой B(4, 6):

Начальная точка A(x1, y1) = A(1, 2).
Конечная точка B(x2, y2) = B(4, 6).
Уравнение прямой, проходящей через точки A и B: y = kx + b.
Составляем систему уравнений: система уравнений для прямой, проходящей через точки A и B:
- Уравнение для точки A: 2 = k * 1 + b.
- Уравнение для точки B: 6 = k * 4 + b.
Решаем систему уравнений: решение системы уравнений дает значения углового коэффициента k = 4/3 и свободного члена b = -2/3.
Проверяем решение, подставляя найденные значения в уравнение и проверяя, что оно соответствует точкам A и B:
- Уравнение для точки A: 2 = (4/3) * 1 — 2/3.
- Уравнение для точки B: 6 = (4/3) * 4 — 2/3.

Таким образом, отрезок AB имеет уравнение прямой y = (4/3)x — 2/3.

Примеры отрезков

1. На фотографии изображен отрезок, соединяющий две разные точки A и B на побережье. Этот отрезок может быть использован для измерения расстояния между этими двумя точками или для обозначения направления.

2. В математике отрезки также могут быть представлены на координатной плоскости. Например, отрезок AB имеет начальную точку A (2, 3) и конечную точку B (5, 7). Этот отрезок может быть использован для определения угла наклона или для нахождения евклидова расстояния между точками A и B.

3. В геометрии отрезки могут быть использованы для построения треугольника или других многоугольников. Например, отрезки BC, CD и DA могут быть использованы для построения треугольника ABC.

4. В инженерии и строительстве отрезки часто используются для обозначения размеров и расстояний. Например, отрезок ACO может обозначать длину балки или отрезок DC может обозначать ширину дверного проема.

Все эти примеры показывают, что отрезки — это полезные инструменты, которые используются в различных областях знаний для измерения, обозначения и построения. Они имеют начальную и конечную точки, которые определяют их длину и форму.

Математика – это просто!

ПЛОСКИЕ ФИГУРЫ: · Отрезок, луч, прямая
· Угол
· Разновидности углов
· Признаки параллельности
МНОГОУГОЛЬНИКИ: · Виды треугольников
· Биссектриса и высота
· Признаки равенства треугольников
· Равнобедренные треугольники
· Площадь треугольника
· Теорема Пифагора
· Теорема синусов
· Теорема косинусов
· Подобные треугольники
· Параллелограмм
· Ромб, квадрат
· Трапеция
ОКРУЖНОСТЬ и КРУГ: · Что такое окружность
· Что такое круг
· Касательная к окружности
· Вписанная окружность
· Описанная окружность
ВЕКТОРЫ: · Что такое вектор
· Сложение и вычитание векторов
· Умножение вектора на число
· Координаторы вектора
· Угол между векторами
· Скалярное произведение векторов
НАТУРАЛЬНЫЕ ЧИСЛА
ДРОБИ
УРАВНЕНИЯ и ТОЖДЕСТВА
ОДНОЧЛЕНЫ и МНОГОЧЛЕНЫ
ФУНКЦИИ
ТРИГОНОМЕТРИЯ
ВЫСШАЯ МАТЕМАТИКА

Определение понятий луч и прямая

Луч – это линия, образованная точкой (началом луча) и бесконечно продолжающаяся в одном направлении. Точка, из которой луч начинается, называется началом луча, а направление, в котором луч продолжается, называется направлением луча. Луч не имеет конечной длины и может быть направлен вправо, влево, вверх или вниз.

Прямая – это линия, которая не имеет начала и конца, и бесконечно продолжается в обоих направлениях. Прямая имеет постоянное направление и не имеет изгибов, она простирается до бесконечности. Прямая может быть вертикальной (параллельной оси OY), горизонтальной (параллельной оси OX) или наклонной (не параллельной ни OX, ни OY).

Основная разница между лучом и прямой заключается в том, что луч имеет начало и продолжается в одном направлении, в то время как прямая не имеет начала и конца и продолжается в обоих направлениях. Кроме того, луч можно ограничить, указав конечную точку на нем, в то время как прямая не имеет конечной точки.

Понятие	Особенности
Луч	— Имеет начало и продолжается в одном направлении— Может быть ограничен конечной точкой
Прямая	— Не имеет начала и конца, продолжается в обоих направлениях— Не имеет изгибов

Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°

Длинный отрезок «поломали» на несколько коротких

Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.

Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.

Обозначается ломанная перечислением всех её вершин.

звено CD и звено DE являются смежными

Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305

Задача: какая ломанная длиннее
, а у какой больше вершин
? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.

Сравнение

Из определений видно, что кардинальное отличие луча от прямой заключается в том, ограниченны ли они в пространстве. Так, луч обязательно имеет начало и продолжается только с одной стороны. У прямой, в свою очередь, нет предела ни с того, ни с другого края. В связи с этим начертить можно лишь ее часть, что, впрочем, относится и к лучу.

Если взять на прямой произвольную точку, то отходящая от нее бесконечная линия будет являться лучом. В этом смысле луч можно назвать частью прямой. Справедливо и то, что избранная точка будет служить в качестве исходной сразу для двух противоположно направленных лучей.

Сравнивая луч и прямую, следует сказать о способах их обозначения. Каждый из геометрических объектов может называться латинской строчной буквой: луч a (с, d, t) или прямая b (a, h, c). Также в том и другом случае используется обозначение двумя заглавными буквами: луч NK или прямая OD.

Однако в последнем пункте имеются отличия. Буквы в названии прямой, помечающие точки, через которые она проведена, при чтении и записи можно менять местами. Между тем относительно луча первым указывается строго его начало, а затем точка, расположенная на определенном расстоянии от исходной.

Кроме того, луч имеет собственный вариант обозначения. В этом случае после заглавного символа, называющего начальную точку, с помощью строчной буквы указывается прямая, на которой расположен луч. Таким образом, обозначение Bo трактуется так: луч с началом в точке B принадлежит прямой o.

В чем разница между лучом и прямой, кроме сказанного? В том, что лучи могут образовывать угол. Для этого они должны исходить из одной точки. Прямые углов не образуют.

Где используют луч

Луч используется в геометрии и физике.

В геометрии, луч — это одно из основных понятий, чтобы описать линию, проходящую через две точки. Луч — это часть прямой, которая имеет начальную точку и продолжается в бесконечность. Луч используется для описания простых геометрических фигур, таких как треугольник, прямоугольник, круг и другие.

В физике, луч используется для описания пути света и других электромагнитных волн. Луч света — это кусок пути, пройденный светом в определенном направлении. Луч используется при изучении оптики и электромагнетизма.

Также луч используется в радиотехнике и телекоммуникациях для описания беспроводных сигналов, передаваемых через пространство.

Принципы классификации

Так как луч является частью прямой, поэтому через любую его точку проводится множество прямых, но только через две несовпадающие проходит одна прямая. Луч можно изобразить в нескольких вариантах: пересечение, скрещивание и параллельность.

Чтобы задать луч на плоскости, используется линейное уравнение. Фигуры называются разными способами и с помощью знаков. Можно провести полупрямую «О». Её начальная точка считается исходной и другой не существует. Другой способ записи — использование нескольких букв в середине либо в иных частях линии. Если в задаче дана прямая, её можно обозначить двумя буквами, размещёнными в разных её частях, к примеру, (АB).

Третий метод обозначения: точка «О» находится с некоторым отступом от начала. Центральную часть можно назвать буквой К. В таком случае весь луч будет называться ОК. Если нужно начертить продолжение к прямой, понадобится отметить на чертеже линию и точку, которая будет считаться производной. С помощью последней фигуры делится первая на 2 линии, которые не пересекаются между собой. Чтобы обозначить продолжение, рисуется линия карандашом.

Она будет иметь общее начало с основополагающей, но не будет совпадать с ней. Из т. О проводится прямая, не располагающаяся на дополняющих, но имеющая с ними одно общее начало. На новом луче отмечается т. В. На продолжении лежит отрезок ОВ.

Неразвернутый угол является случаем луча. Если стороны первой фигуры представлены в виде дополнительных полупрямых одной прямой, тогда угол является развёрнутым. Его значение равняется 180 градусов. Если значение угла иное, тогда он неразвернутый.

В математике фигура представлена в виде линии, у которой нет ничего общего с энергией. Для световых лучей характерно несконцентрированное направление, дефракция (переломанный). Но при сильном потоке света наблюдается их чёткое направление.