Чем дифференциал отличается от производной: примеры, определение и связь

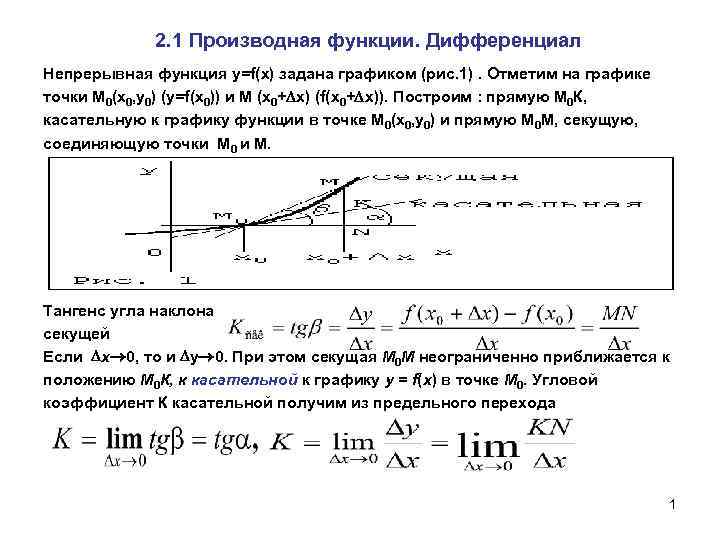
Первый дифференциал функции

Определение первого дифференциала функции

Дифференциал функции в точке: Пусть функция дифференцируема в некоторой точке . Тогда ее приращение в этой точке можно представить в виде суммы линейной функции от приращения ее аргумента и по сравнению с .Дифференциалом функции в точке называется главная линейная часть приращения функции, соответствующая приращению независимой переменной . То есть это приращение функции, в котором опущены слагаемые, содержащие бесконечно малые величины по сравнению с приращением аргумента . Дифференциал обозначается как или , и является функцией двух переменных: и . Он также называется дифференциалом первого порядка или первым дифференциалом.
Дифференциал независимой переменной: – это приращение аргумента функции:. Он является независимой переменной.

С учетом определений, дифференциал функции имеет следующий вид.(1.1) . Его также можно записать в одной из следующих форм.;;.

Поскольку дифференциал функции зависит от двух переменных, то его следовало бы писать так: . Однако, переменную , как правило опускают, и пишут сокращенно . При этом всегда подразумевают ее присутствие. То есть сначала мы вводим новую независимую переменную , являющуюся приращением аргумента функции, а затем, используя две независимые переменные и , определяем дифференциал.

В чем смысл первого дифференциала

Зачем вводят дифференциалы? Не проще ли использовать вместо них приращения независимой переменной и функции? – Дифференциалы вводят для сокращения записей расчетов, в которых используются стремящиеся к нулю приращения. На завершающем этапе таких расчетов выполняют предельный переход, в результате которого все о – малые функции от приращений стремятся к нулю. Поэтому применяют систему записи, в которой эти о – малые исключены с самого начала.

В строгом варианте, нужно выписать точные выражения для приращений, типа. По завершении алгебраических операций, выполнить предельный переход при , . Вместо этого с самого начала оставляют только главные части приращений, которые называются дифференциалами:. В результате получают выражения, линейные по дифференциалам, справедливые для приращений, когда они стремятся к нулю.

Можно сказать и так.Дифференциалы – это приращения, в которых отброшены все функции, о – малые от приращений независимых переменных.Первые дифференциалы – это выражения, в которых оставлены только линейные части приращений. Также говорят, чтоДифференциалы – это бесконечно малые приращения.

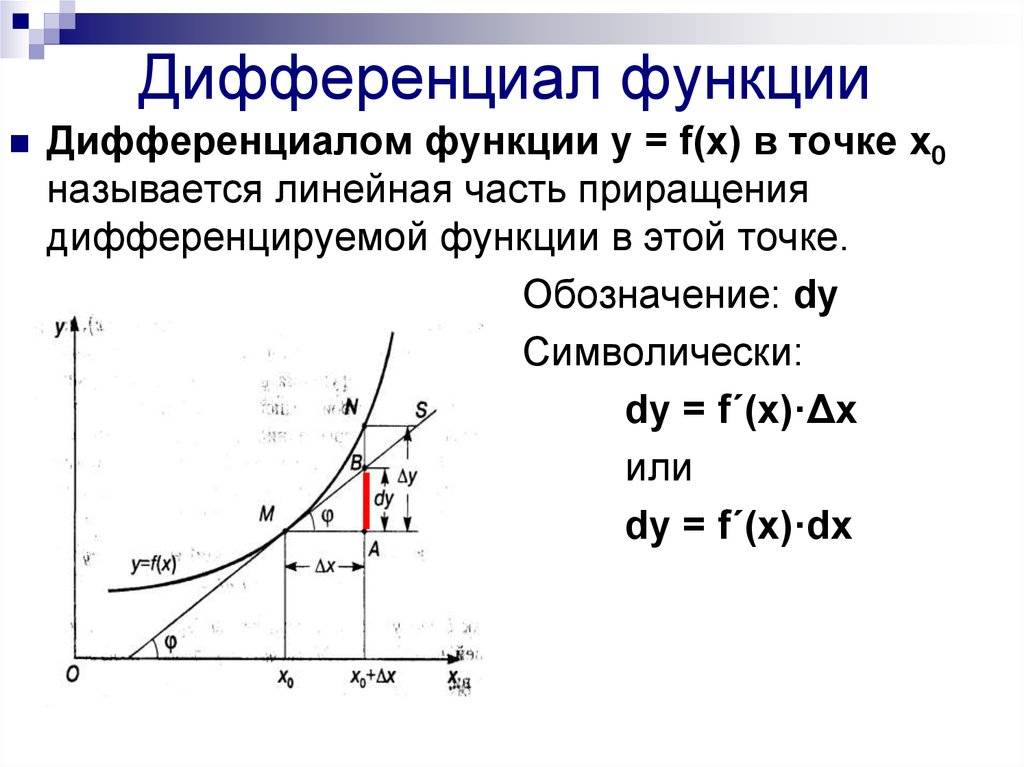
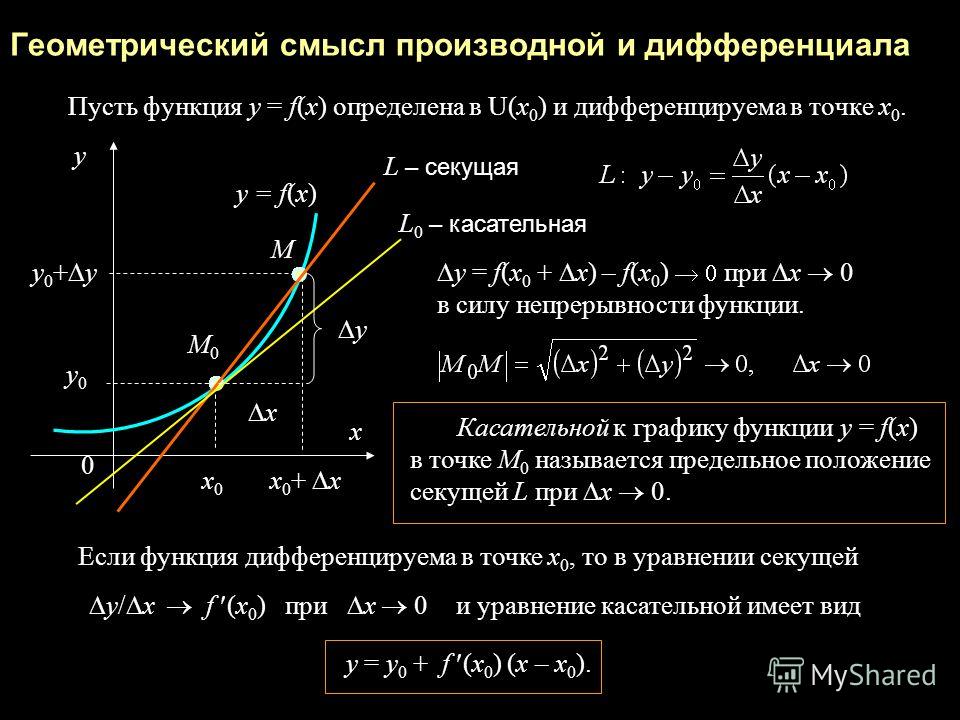
Геометрический смысл дифференциала

Если существует конечная производная функции в точке , то дифференциал функции в точке – это приращение ординаты касательной, проведенной к графику функции в точке , соответствующее приращению аргумента . Дифференциал независимой переменной – это приращение аргумента функции: .
Дифференциал функции в точке x – это приращение ординаты касательной, проведенной к графику в этой точке. Доказательство

На странице «Геометрический смысл производной» мы выяснили, что уравнение касательной к графику функции имеет вид:(1.2) , где .

В точке с абсциссой , ордината касательной равна . Рассмотрим точку , в которой приращение абсциссы равно . Из уравнения находим ординату касательной в этой точке:. Приращение ординаты касательной. Как видно, оно совпадает с дифференциалом функции в точке .

Свойства первого дифференциала

Арифметические свойства дифференциалов

Теорема Пусть функции и дифференцируемы в точке ; – постоянная. Тогда в этой точке(1.3) (дифференциал суммы функций);(1.4) (дифференциал произведения);(1.5) , при (дифференциал частного). Постоянный множитель можно выносить из-под знака дифференциала:(1.6) .

Доказательство следует из определения дифференциала и .;;;.

Инвариантность формы первого дифференциала

Теорема Пусть функцию можно представить как сложную: . При этом функция имеет производную в точке , а функция имеет производную в точке . Тогда дифференциал первого порядка функции, выраженный через переменную имеет ту же форму, что и дифференциал, выраженный через переменную . Эту же формулу можно записать так:.
Доказательство

По , в точке существует производная по . Применим эту теорему и подставим ..

Здесь мы выполнили доказательство, использую характеристики функций . Проделаем тоже самое, использую переменные ..

Можно проделать вывод и просто сделав подстановку .. В известном смысле с первыми производными можно обращаться как с дробями, составленными из дифференциалов.

Примечание. В формуле , является дифференциалом независимой переменной, то есть приращением переменной . В формуле , уже дифференциал зависимой переменной. Он может отличаться от приращения на о – малое по сравнению с при .;.

Дифференциал функции

Если
функция
дифференцируема в точке,то её
приращение можно представить в виде
суммы двух слагаемых

.
Эти слагаемые являются бесконечно
малыми функциями при .

Первое слагаемое
линейно относительно ,второе является
бесконечно малой более высокого порядка,
чем

png» width=»28″>.Действительно,

Таким образом второе слагаемое
при быстрее стремится к нулю и при нахождении
приращения функцииглавную роль играет первое слагаемоеили (так как).
Определение.Главная часть
приращения функции
в точке ,
линейная относительно,называется
дифференциалом функциив этой точке
и обозначается dy или df(x)
. (2)
Таким
образом, можно сделать вывод: дифференциал
независимой переменной совпадает с её
приращением, то есть .
Соотношение
(2) теперь принимает вид
(3)
Замечание.
Формулу (3) для краткости часто записывают
в виде
(4)

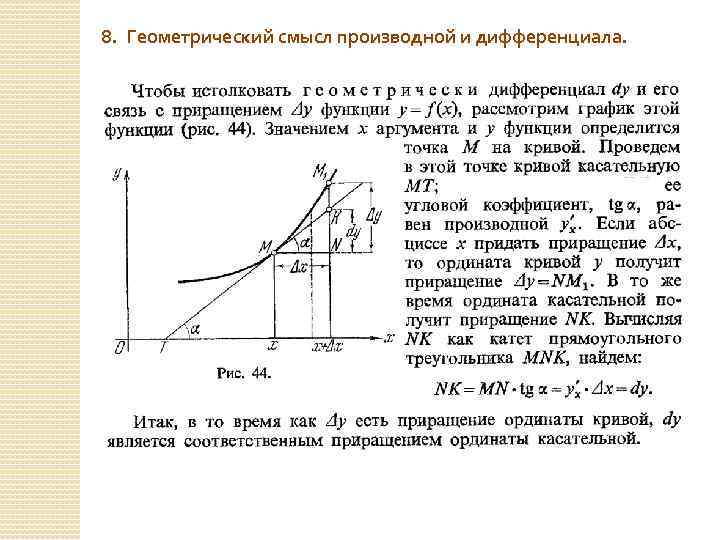
Геометрический смысл дифференциала

Рис.2

Рассмотрим
график дифференцируемой функции .
Точкиипринадлежат графику функции.

В точкеМпроведена
касательная К к графику
функции, угол которой с положительным
направлением оси обозначим через.

Проведем прямыеMN параллельно
оси Ox и параллельно осиOy.
Приращение функции равно длине отрезка
.
Из прямоугольного треугольника

Q4d2/img-yjde73.png» width=»44″>, в котором,
получим

Изложенные выше
рассуждения позволяют сделать вывод:

Дифференциал
функции
в точке изображается приращением ординаты
касательной к графику этой функции в
соответствующей её точке.

Связь дифференциала с производной

Рассмотрим
формулу (4)

Разделим
обе части этого равенства на dx
, тогда

Таким
образом, производная
функции равна отношению её дифференциала
к дифференциалу независимой переменной.
Часто
это отношение рассматривается просто как символ,
обозначающий производную функцииу по аргументу х.
Удобными
обозначениями производной также
являются:
, и так далее.
Употребляются также записи
, ,
особенно
удобные, когда берется производная от
сложного выражения.

2. Дифференциал суммы, произведения и частного

Так
как дифференциал получается из производной
умножением её на дифференциал независимой
переменной, то, зная производные основных
элементарных функций, а также правила
для отыскания производных, можно прийти
к аналогичным правилам для отыскания
дифференциалов.
10.Дифференциал
постоянной равен нулю
.
20.Дифференциал
алгебраической суммы конечного числа
дифференцируемых функций равен
алгебраической сумме дифференциалов
этих функций

30.

Дифференциал
произведения двух дифференцируемых
функций равен сумме произведений первой
функции на дифференциал второй и второй
функции на дифференциал первой

Следствие.Постоянный
множитель можно выносить за знак
дифференциала

Пример.
Найти дифференциал функции .

Решение.Запишем данную
функцию в виде

тогда
получим

4. Функции, заданные параметрически, их дифференцирование

Определение.Функция
png» width=»59″>называется заданной параметрически,
если обе переменныех и у определяются
каждая в отдельности как однозначные
функции от одной и той же вспомогательной
переменной – параметра t
png»>
где t изменяется в пределах .

Замечание.
Параметрическое задание функций широко
применяется в теоретической механике,
где параметр t обозначает
время, а уравнения

png» width=»24″>представляют собой законы изменения
проекций движущейся точкина осии.

Замечание.
Приведем параметрические уравнения
окружности и эллипса.

а)
Окружность с центром в начале координат
и радиусом rимеет
параметрические уравнения:
где .
б)
Запишем параметрические уравнения для
эллипса:

где
.
Исключив
параметр t из
параметрических уравнений рассматриваемых линий, можно прийти к их каноническим
уравнениям.
Теорема.
Если функция у от аргумента х задана
параметрически уравнениями ,
гдеидифференцируемые поt
функции и ,
то
.

Пример.
Найти производную функции у
от х ,
заданной параметрическими уравнениями.

Как найти производную и дифференциал функции

Вычисление производной

Первый способ вычислить производную функции — это просто вычислить ее предел. Если он существует, значит, у вас есть производная, иначе вы знаете, что функция не дифференцируема.

Пример:

В качестве функции возьмем f(x) = x2.

\((f(x+h)-f(x))/h = ((x+h)2 – x2)/h = (x2 + 2xh +h2 – x2)/h = 2x + h\)

Теперь нам нужно взять предел для h, чтобы увидеть 0:

f'(x) = 2x.

Вычисление производной функции может стать намного проще, если использовать некоторые свойства:

Правило суммы: (af(x)+bg(x))’ = af'(x) + bg'(x)

Правило квотирования: (f(x)/g(x))’ = (f'(x)g – f(x)g'(x))/g(x)2

Правило произведения: (f(x)g(x))’ = f'(x)g(x) + f(x)g'(x)

Правило цепочки: f(g(x))’ = f'(g(x))g'(x)

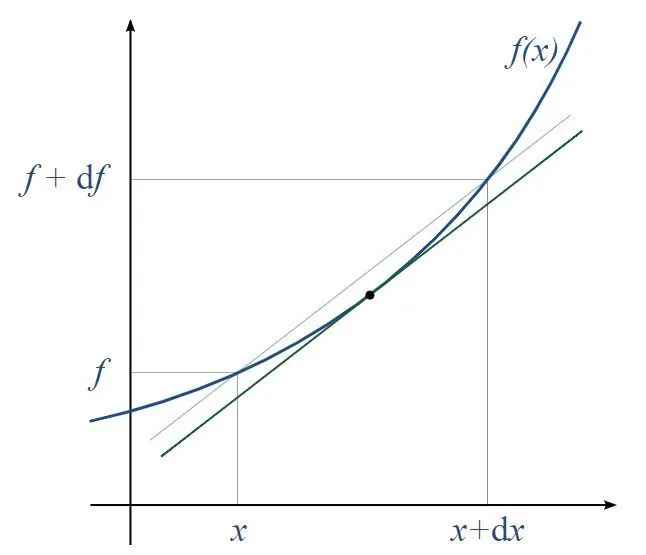
Производная встречается во многих математических задачах. Примером может служить нахождение касательной к линии функции в определенной точке. Чтобы получить наклон этой линии, понадобится производная для нахождения наклона функции в этой точке.

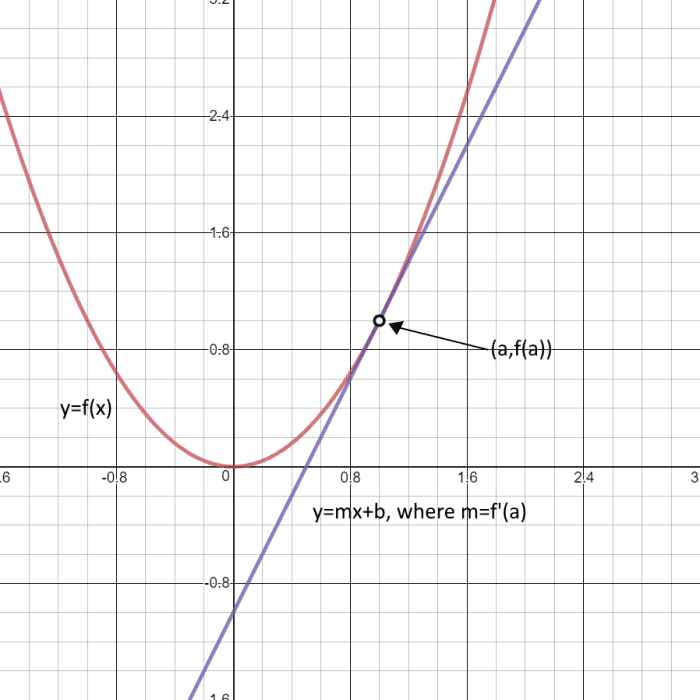
Другое применение — поиск экстремальных значений функции, то есть (локального) минимума или максимума функции. Поскольку в минимуме функция находится в точке минимума, наклон переходит от отрицательного значения к положительному. Поэтому производная равна нулю в минимуме и наоборот: она также равна нулю в максимуме.

Многие физические явления описываются дифференциальными уравнениями. В этих уравнениях есть производные, а иногда и производные более высокого порядка (производные производных). Решение этих уравнений позволяет многое узнать, например, о динамике жидкостей и газов.

Знание следующих правил облегчит расчет производных.

Многочлены

Многочлен — это функция вида a₁ xn + a₂xn-1 + a₃ xn-2 + … + a_nx + a_n+1.

Таким образом, многочлен — это сумма нескольких членов вида axc. Поэтому по правилу суммы, если мы теперь имеем производную каждого члена, мы можем просто сложить их, чтобы получить производную многочлена. Этот случай известен, и мы его получили: d/dx xc = cxc-1

Тогда производная многочлена будет: na₁ xn-1 + (n-1)a₂xn-2 + (n-2)a₃ xn-3 + … + a_n

Экспоненты и логарифмы

Экспоненциальная функция ex обладает тем свойством, что ее производная равна самой функции. Поэтому: d/dx ex = ex

Найти производную других степеней e можно с помощью цепного правила. Например, \(e2x^2\) — это функция вида f(g(x)), где f(x) = ex и g(x) = 2×2. Тогда производная по правилу цепочки становится равной 4x \(e2x^2\).

Если основанием экспоненциальной функции является не e, а другое число a, то производная будет другой.

d/dx ax = ax ln(a), где ln(a) — натуральный логарифм от a.

Производная логарифма 1/x в случае натурального логарифма и 1/(x ln(a)) в случае логарифма с основанием a.

Отрицательные и дробные числа

d/dx xc = cxc-1 выполняется и в том случае, если c — отрицательное число, поэтому, например:

1/x = x-1

d/dx 1/x = -1/x2

Более того, она справедлива и при дробном c. Это позволяет нам вычислять производную, например, квадратного корня:

\(d/dx sqrt(x) = d/dx x1/2 = 1/2 x-1/2 = 1/2sqrt(x)\)

Гониометрические функции

Синус, косинус и тангенс также имеют производную.

d/dx sin(x) = cos(x)

d/dx cos(x) = – sin(x)

d/dx tan(x) = 1 – tan2(x)

d/dx arcsin(x) = 1/sqrt(1-x2)

d/dx arccos(x) = -1/sqrt(1-x2)

d/dx arctan(x) = 1/(1+x2)

Вычисление дифференциала

Предположим, что существует функция f(x) = x2. Наклон этой функции в определенной точке, скажем, 3, можно определить с помощью дифференциального исчисления. Производная этой функции будет f'(x) = 2x. Подставив в это уравнение x = 3, получим f'(x) = 6. Таким образом, наклон касательной линии при x = 3 равен 6.

Различные формулы дифференциального исчисления используются для нахождения производных различных типов функций. Согласно определению, производная функции может быть определена следующим образом:

\(f'(x) = limh→0 f(x+h)-f(x) / h\)
Ниже приведены важные формулы дифференциального исчисления для различных функций:

Элементарные:

d/dx ex = ex
d/dx ax = ax. ln .a , где a > 0, a ≠ 1
d/dx ln x = 1/x, x > 0
d/dx √x = 1/(2 √x)

Гиперболические:

d/dx sinhx = coshx
d/dx coshx = sin hx

d/dx tan hx = sec h2x
d/dx cot hx = -cosec h2x

d/dx sec hx = -sech hx tan hx
d/dx cosec hx = -cosec hx cot hx

Тригонометрические:

d/dx sin x = cos x
d/dx cos x = -sin x
d/dx tan x = sec2 x , x ≠ (2n + 1) π / 2 , n ∈ I
d/dx cot x = – cosec2 x, x ≠ nπ, n ∈ I
d/dx sec x = sec x tan x, x ≠ (2n + 1) π / 2 , n ∈ I
d/dx cosec x = – cosec x cot x, x ≠ nπ, n ∈ I

Правила дифференцирования

1. Производная суммы или разности
2. Производная произведения
2a. Производная выражения, умноженного на постоянный множитель
3. Производная частного
4. Производная сложной функции

Правило 1. Если функции

дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции

причём

т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.

Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны, т.е.

Правило 2. Если функции

дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение

причём

т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.

Следствие 1. Постоянный множитель можно выносить за знак производной:

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.

Например, для трёх множителей:

Правило 3. Если функции

дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём

т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.

Где что искать на других страницах

При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные – в статье “Производная произведения и частного функций”.

Здесь же (далее) – более простые примеры на производную произведения и частного, на которых Вы увереннее освоите алгоритмы вычислений.

Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме
и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она
выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных,
но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.

А если при дифференцировании произведения или частного у вас появилось слагаемое
, в котором – число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).

Другая частая ошибка – механическое решение производной сложной
функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.

По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.

Если Вы ищете решения производных дробей со степенями и корнями,
то есть, когда функция имеет вид вроде , то
следуйте на занятие “Производная суммы дробей со степенями и корнями”.

Если же перед Вами задача вроде ,
то Вам на занятие “Производные простых тригонометрических функций”.

[Математика] Определение дифференциала, разница между дифференциалом и производной

http-equiv=”Content-Type” content=”text/html;charset=UTF-8″>style=”clear:both;”>

В этой статье мы подробно определим дифференциал и объединим понятие производной, чтобы подробно объяснить разницу между ними.

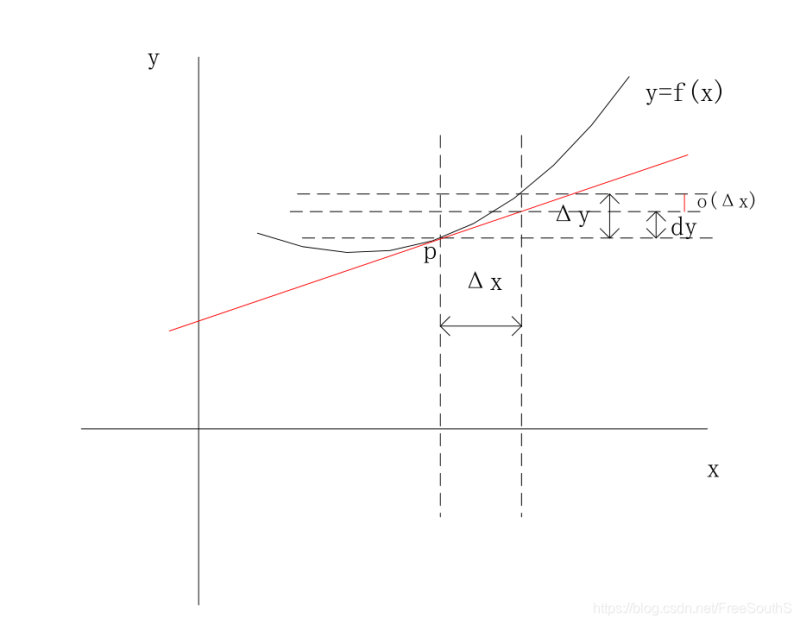
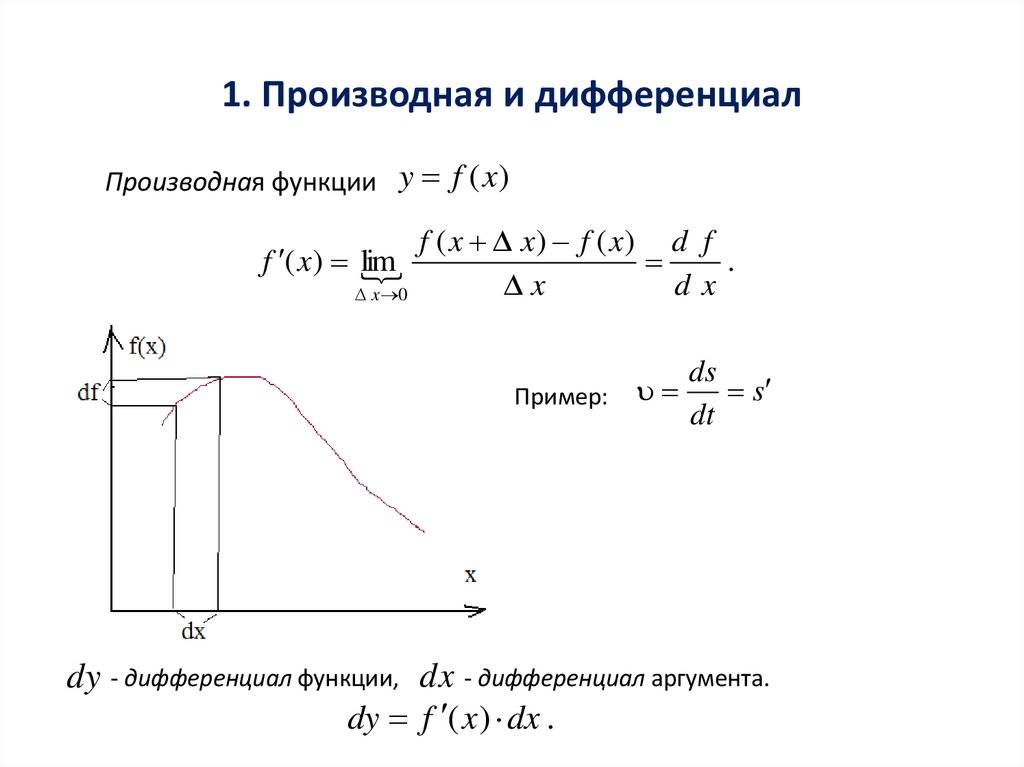
Как показано на рисунке выше, для функции y = f (x) в любой точке p (x, y), если есть приращение в направлении x, То есть приращение по оси y, когдаКогда производная определяется как

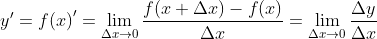
Можно видеть, что производная связана с соотношением между ними, когда изменяется x и изменяется y. Дифференциал определяется как незначительное изменение x, Небольшое изменение направления y, Из формулы производной находим

, Вы можете иметьТогда да，

И наконец:(Формула 1)

среди нихзаБесконечно малое число высокого порядка, то есть когдавПри приближении к 0, тоБыстрее сходятся к 0, поэтому скорость изменения в направлении yВести себя как иЛинейная связь. Ты можешь видетьНаходится ли f (x) вПроизводная при является независимымКогда фиксированное значение (уравнение 1) удовлетворяется, мы называем y = f (x) вГде дифференцируемо, а dy =Называется y = f (x) вДифференциал на месте.

А скорость изменения в направлении x dx =затемЭто основная дифференциальная формула. По сравнению с уравнением 1 мы разные, То есть дифференциал является приближением. ПосмотримПроизводная этой функции:

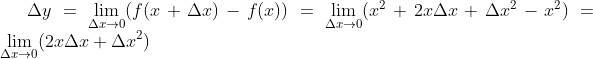
Среди них мы видим, что 2x – производная, аТолькоБесконечно малое число высокого порядка.

Есть пределы, дифференцируемые, и дифференцируемые слева и справа устанавливаются взаимно, поэтому

Это знаменитая дифференциальная формула.

Интеллектуальная рекомендация

Основная элементарная функция Элементарная функцияПоОсновная элементарная функцияФункция получается после конечного числа из четырех операций и составных операций.Основная элементарная функцияИ элемен…

Ссылочный блогhttps://blog.csdn.net/baishuo8/article/details/81408369И знатьhttps://www.zhihu.com/question/36301367 I. Производная производныйНаш самый ранний контактУнарная функцияЭто можно легко наб…

1. Пограничные разницы: Дерево, пусть права границы на пути x-> y добавьте w: d += w, d += w, d -= 2*w; Наконец, найдите f : я использую I как детское дерево, D of of of of. То…

Одна измеренная разница Дифференциальная концепция Для ряда столбцов a_ {i} данные, которые мы должны сохранить, – это «разница между двумя соседними числами». Эта стратегия, порядок p i =…

Из -за приготовления дерева он узнал разницу между деревом. Разница точек: вся точка мощности +1 на пути u-v, затем C ++, C ++, C -, C ]-, может быть многократно много раз после …

Вам также может понравиться

В предыдущем разделе мы изучили «Ортогональную матрицу и матричную QR-декомпозицию», на этот раз мы продолжаем содержание предыдущего раздела, чтобы узнать «производную от вектора&ra…

1. Производная 1.1 Обычно используемые взаимные 1.2 Вывод составных функций 1.2.1 Цепное правило 1.2.2 Производные многомерных функций: частные производные (частный дифференциал) 2. Очки Определенный …

Сегодняшнее главное преимущество состоит в том, что я прекращаю готовить каждый раз, когда получаю вывод функции, но все равно часто использую ее. Что ж, сегодня я наконец-то добился своего главного п…

команда diff ПозвонивdiffКоманда для вычисления символьной производной: Чтобы получить производную более высокого порядка, используйте: Давайте посмотрим на пример и найдем его вторую производную: Мы …

= Представляет назначение == это означает, что он не сравнивает тип данных, только значение var a=’0′; a==0;//true === Хенг и др., Значение левой и правой стороны и тип данных равны ! = Типы данных с …

Основные различия между дифференциалами и производными

Основное различие между дифференциалами и производными заключается в их определениях, которые тем самым влияют на их функциональность в математической сфере. Первый – это подобласть исчисления, которая подразумевает бесконечно малую разницу в некоторой колеблющейся величине. С другой стороны, производные относятся к изменению выходного значения из-за соответствующего изменения входного значения. Это означает скорость этого изменения.
Дифференциальные уравнения содержат производные или функции от производных
Принимая во внимание, что производные просто относятся к мгновенному изменению, которое происходит с изменением независимой переменной, которое вызывает соответствующее изменение значения зависимой переменной.
Функциональная связь между зависимыми и независимыми переменными известна в случае производной и неизвестна в случае дифференциала

Это представляет собой еще одно важное различие между двумя математическими концепциями.
Формулы дифференциального и производного уравнения также существенно различаются
dy / dx = f (x) представляет первую, где y – зависимая, а x – независимая переменная. Производные представлены как d / dx.
Дифференциалы представляют изменение реального значения на линейной карте, а производные представляют такое же изменение на карте уклона

Производные вычисляют наклон функции на графике в любой момент времени.

Дифференциал и производная

Пусть функция f определена в некоторой окрестности точки x . Тогда обозначим \Delta y = f(x + \Delta x) — f(x) .

Очевидно тогда, что \lim\limits_ \Delta y = 0 .

С целью более подробного изучения \Delta y она линеаризуется по x . Отсюда возникает понятие дифференциала.

o(\Delta x) — такая величина, что \frac \to 0 при \Delta x \to 0 . Тогда A(x)\Delta x называют дифференциалом в точке x .

Если функция дифференцируема, то \frac = A(x) + \frac ,

Определение:

f'(x) = \lim\limits_ \frac

Проблему дифференцирования сводят к проблеме существования производных, поэтому для функций одной переменной дифференцируемость равносильна существованию производной ( dy = f'(x)\Delta x ). Однако, это верно только для функций одной переменной.

Легко понять, что если функция дифференцируема, то она непрерывна в этой точке. Однако, обратное может быть неверно. Например, функция y = |x| в точке x = 0 . В этой точке у неё нет производной, значит, она не дифференцируема.

Стандартные арифметические свойства производной

(f + g)’ = f’ + g’
(fg)’ = f’g + g’f
\left(\frac\right)’ = \frac

Докажем, например, второе свойство.

Дифференцируемость сложной функции

Большое значение имеет правило дифференцирование сложной функции.

То, что из дифференцируемости следует непрерывность позволяет доопределить по непрерывности \Delta x = 0 и считать, что o(\Delta x) = \left\ 0 & , \Delta x = 0\\ o(\Delta x) & , \Delta x \ne 0\\ \end\right. . Это мотивировано непрерывностью функции в точке x .

По определению дифференциала \Delta z = g(y_0 + \Delta y) — g(y_0) = g'(y_0)\Delta y + o(\Delta y) и \Delta y = f(x_0 + \Delta x) — f(x_0) = f'(x_0)\Delta x + o(\Delta x)

g определена в окрестности точки y_0 . Так как \Delta y \to 0 при \Delta x \to 0 и y_0 = f(x_0) , то при \Delta x \to 0 , f(x_0 + \Delta x) принадлежит окрестности точки y_0 .

Тогда функция z = g(f(x)) при x = x_0 + \Delta x, \ \Delta x \to 0 корректно определена.

\Delta y = f(x_0 + \Delta x) — f(x_0)

\Delta g = g(f(x_0) + (f(x_0 + \Delta x) — f(x_0))) — g(f(x_0)) = g(f(x_0 + \Delta x)) — g(f(x_0)) = (по определению дифференциала для g(y) ) g'(y_0)(f(x_0 + \Delta x) — f(x_0)) + o(\Delta y) = (по определению дифференциала для f(x) ) g'(y_0)f'(x_0)\Delta x+ g'(y_0) o(\Delta x) + o(\Delta y)

Итого получаем: \Delta g = g'(y_0)f'(x_0)\Delta x + g'(y_0)o(\Delta x) + o(\Delta y)

Устремляя \Delta x \to 0 , получаем dz = g'(y_0)f'(x_0)\Delta x

Для полного счастья осталось доказать, что o(\Delta x) = o(\Delta y) .

По определению o(\Delta y) , получаем: \forall \varepsilon \gt 0 \ \exists \delta \gt 0 : \ |\Delta y| \lt \delta \Rightarrow \left|\frac\right| \leq \varepsilon

Последнее неравенство равносильно следующему: |o(\Delta y)| \leq \varepsilon |\Delta y|

\Delta y = f(x_0 + \Delta x) — f(x_0) = f'(x_0)\Delta x + o(\Delta x) = \Delta x(f'(x_0) + o(1)) , где o(1) = \frac , что стремится к 0 .

Из всего этого следует, что при \Delta x \to 0 , \Delta y \to 0 для имеющегося \delta \gt 0 .

Производные высших порядков

Определение. Второй производной (или производной второго порядка) функции y=f(x) называется производная от ее первой производной.

Обозначение второй производной функции y=f(x):

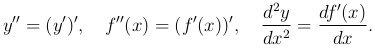
Механический смысл второй производной. Если функция y=f(x) описывает закон движения материальной точки по прямой линии, то вторая производная f″(x) равна ускорению движущейся точки в момент времени x.

Аналогично определяется третья, четвертая производная.

Определение. n-й производной (или производной n-го порядка) функции y=f(x) называется производная от ее n-1-й производной:

y(n)=(y(n-1))′, f(n)(x)=(f(n-1)(x))′.

Обозначения: y″′, yIV, yV и т.д.

Применение в науке и технике

Понятие дифференциала имеет широкое применение в различных областях науки и техники. Оно используется для анализа и описания различных процессов и явлений, а также для построения математических моделей.

Механика

В механике дифференциалы используются для описания движения тел. Они позволяют определить скорость и ускорение объекта в каждый момент времени. При решении задач на механику дифференциалы позволяют получить более точные результаты и учесть изменения параметров системы.

Физика

В физике дифференциалы используются для описания различных законов и закономерностей. Например, в термодинамике они позволяют описать изменение температуры и давления в системе. В оптике дифференциалы используются для описания распространения света и его взаимодействия с материалами.

В области электроники дифференциалы используются для анализа и проектирования различных электрических схем. Они позволяют учесть изменение величин токов и напряжений в каждом элементе схемы и определить их влияние на работу всей системы.

Математика

В математике дифференциалы используются для определения производных функций и решения дифференциальных уравнений. Они являются основным инструментом в исследовании функций и их свойств. Дифференциалы также широко применяются в численных методах решения математических задач и моделирования.

Дифференциалы применяются в физике для описания законов природы и процессов, происходящих в материальных объектах.
В механике дифференциалы используются для анализа движения тел и определения их скорости и ускорения.
В электронике дифференциалы используются для анализа электрических схем и определения их характеристик.
В математике дифференциалы используются для решения дифференциальных уравнений и исследования функций.

Дифференциальные функции. Определение дифференциала.

Определение. Функция у = f(х) называется дифференцированной в точке х, если её приращение Dу в этой точке можно представить в виде
Dу = f’(х)Dх+a(Dх)Dх,
где a (Dх) = 0
Как видно из из определения, необходимым условием дифференцируемости является существование производной. Оказывается что это условие также и достаточно. В самом деле пусть существуют у’ = f’(х)
Положим – f’(х), Dх № 0
0 , Dх = 0
При таком определении a имеет для всех Dх
Dу = f’(х)Dх +a(Dх)Dх .
Остаётся, следовательно, установить непрерывность a(Dх) при Dх = 0, то есть, равенство a (Dх) = a(0) = 0, но, очевидно,
a (Dх) = – f’(х) = f’(х) – f’(х) = 0,
что и требовалось.

Понятие дифференцируемости функции

Пусть функция y=f(x) определена на некотором интервале (a, b), x — некоторое фиксированное значение аргумента из этого интервала, Δx — любое приращение аргумента, такое, что значение аргумента x+Δx ∈ (a, b).

Определение. Функция y=f(x) называется дифференцируемой в данной точке x, если приращение Δy этой функции в точке x, соответствующее приращению аргумента Δx, может быть представимо в виде

Δy = A Δx +αΔx,

где A — некоторое число, не зависящее от Δx, а α — функция аргумента Δx, являющая бесконечно малой при Δx→ 0.

Так как произведение двух бесконечно малых функций αΔx является бесконечно малой более высокого порядка, чем Δx (свойство 3 бесконечно малых функций), то можем записать:

Δy = A Δx +o(Δx).

Теорема. Для того, чтобы функция y=f(x) являлась дифференцируемой в данной точке x, необходимо и достаточно, чтобы она имела в этой точке конечную производную. При этом A=f′(x), то есть

Δy = f′(x) Δx +o(Δx).

Операцию нахождения производной обычно называют дифференцированием.

Теорема. Если функция y=f(x) дифференцируема в данной точке x, то она непрерывна в этой точке.

Замечание. Из непрерывности функции y=f(x) в данной точке x, вообще говоря, не вытекает дифференцируемость функции f(x) в этой точке. Например, функция y=|x| — непрерывна в точке x=0, но не имеет производной.

История развития

История развития дифференциала уходит корнями в XVI век, когда математики начали исследовать и обобщать понятие скорости изменения функции. Одним из первых, кто занимался этой проблемой, был французский математик Рене Декарт.

В XVII веке итальянский ученый Исаак Ньютон и немецкий математик Готфрид Лейбниц независимо друг от друга разработали математическую теорию дифференциала. Они предложили методы нахождения производной функции и основали дифференциальное исчисление.

С течением времени дифференциал и его применение стали все более распространенными. В XIX веке Карл Фридрих Гаусс и Жан-Батист Жельбер разработали понятие дифференциала в более общем виде, добавив его в основы математического анализа.

В XX веке разработка дифференциала и его приложений продолжилась. Вместе с развитием математической физики и общей теории относительности, дифференциал стал неотъемлемой частью современной науки.

Сегодня дифференциал используется во многих областях, таких как физика, экономика, инженерия и информатика. Это мощный инструмент для анализа и моделирования сложных процессов и явлений.