Чем отличается луч от отрезка: сравнение геометрических понятий

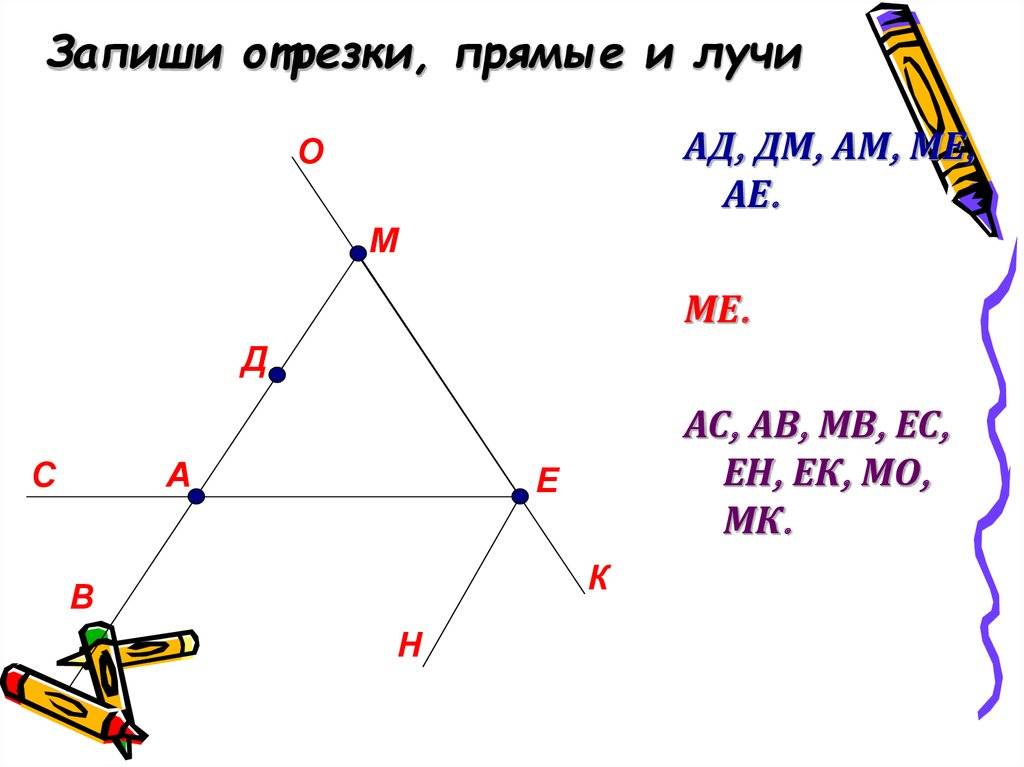
Взаимное расположение лучей

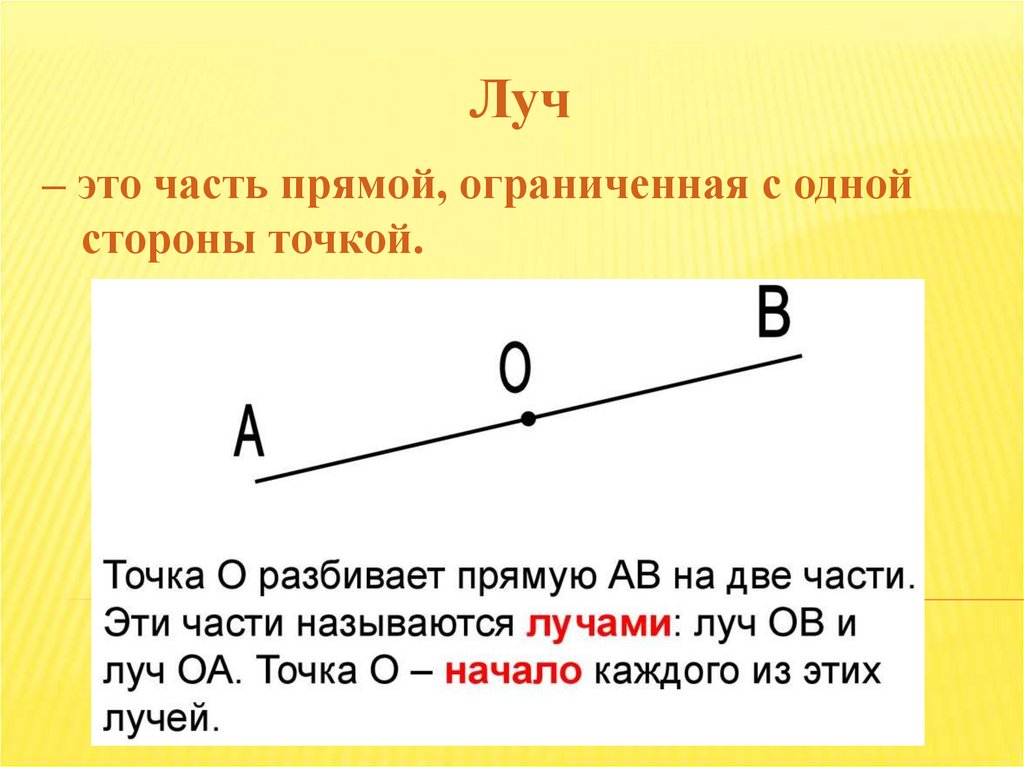
Если поставить точку на прямой, то на ней образуются два таких луча, начало которых находится в одной точке.

На рисунке началом лучей является точка пересечения А.

По обратной схеме лучи делятся на пересекающиеся и непересекающиеся.

Параллельный луч — это фигура, в которой любая точка равноудалена от соответствующей точки другого луча. Параллельные лучи не могут пересекаться.

Дополнительные лучи – это фигуры, которые имеют такие функции, как:

• имеют одинаковое происхождение в одной точке;
• лежит на прямой;
• направлены в разные стороны, то есть угол между ними составляет 180 градусов.

Дополнительные лучи

И все-таки точка делит прямую на два луча — два отдельных друг от друга множества точек. При этом мы, задавая луч в геометрии, как бы делаем упор только на одно из этих возможных множеств

Второе множество точек тоже является важной сопутствующей фигурой и называется дополнительным лучом

Рассмотрим, как дополнительные лучи выглядят на чертеже. Возьмем прямую $a$ и зададим на ней луч $AB$. Чтобы построить к лучу $AB$ дополнительный луч, достаточно отметить точку в противоположном направлении. Итого, луч $AC$ будет являться дополнительным к лучу $AB$. Объединяя оба луча — основной и дополнительный, — мы вновь получаем бесконечную прямую, которой принадлежат лучи.

Нечто вроде формулы: лучи + дополнительные лучи = прямые.

Луч в геометрии — выбор направляющей точки

Отдельно отметим, что выбор направляющей точки, определяющий лучи или дополнительные лучи, может быть произвольным. Добавим на чертеж выше точки $F$ и $G$ и подумаем: в чем отличие между лучами $AB$ и $AF$? Отличаются ли тогда соответствующие дополнительные лучи?

Нет. Выбор направляющей точки условен, поэтому между лучами $AB$ и $AF$ можно установить равенство $AB=AF$. Равные линейные фигуры называются совпадающими.

Важнейшая точка луча  — начальная точка, и если точка начала совпадает для двух лучей, то они представляют собой равные множества точек. Данный вывод распространяется также и на дополнительные лучи.

Дадим определение:

Задача. Дан отрезок $AB$ на прямой $a$. Известно, что точка $C\in{AB}$. Среди лучей $AB$, $AC$, $CA$, $CB$ определите парами совпадающие лучи и дополнительные лучи.

{"questions":,"items":,]},"speech-8":{"type":"speech","text":"Распределите лучи парами. У вас должно получиться две пары — одна дополнительных друг к другу лучей, одна совпадающих."}}}]}

Трудности? Здесь решение!

Скрыть решение

Решение. Из заданных условий видно, что лучи имеют в качестве начальной точки либо точку $A$, либо точку $C$. Рассмотрим вначале лучи $AB$ и $AC$ с общей начальной точкой $A$. Раз $C\in{AB}$, точки $B$ и $C$ лежат по одну сторону от точки $A$. Поэтому делаем вывод, что точки $B$ и $C$ являются направляющими для одного и того же луча. Лучи $AB$ и $AC$ совпадающие.

Теперь рассмотрим пару лучей с начальной точкой $C$ — лучи $CA$ и $CB$. По взаимного расположения точек известно, что из трех точек на прямой одна и только одна лежит между двумя другими.

Точка $C$ принадлежит отрезку $AB$, и, следовательно, точки $A$ и $B$ лежат по разные стороны от точки $C$. Если у лучей $CA$ и $CB$ общая начальная точка, а направляющие располагаются по разные стороны от общей точки, то они будут дополнительными.

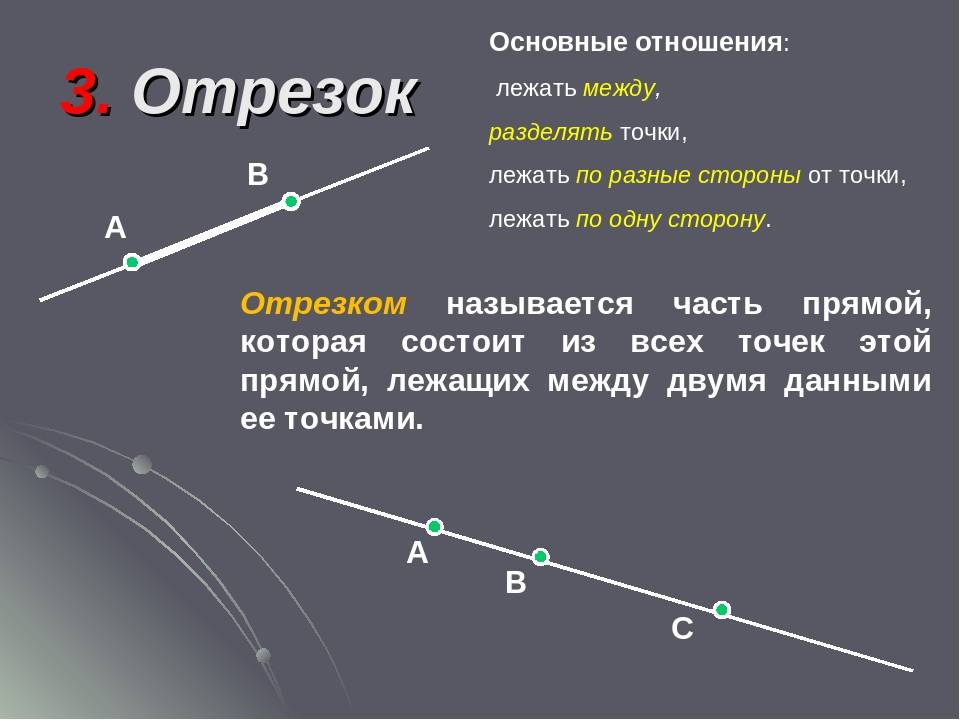
Определение отрезка

Отрезок имеет длину, которая вычисляется как расстояние между его концами. Размер отрезка измеряется с использованием единицы измерения длины, например, сантиметров или метров.

Отрезок может быть горизонтальным, вертикальным или наклонным. Горизонтальный отрезок имеет одинаковые y-координаты для обоих концов, вертикальный отрезок имеет одинаковые x-координаты, а наклонный отрезок имеет разные x- и y-координаты для концов.

Отрезок также может быть выражен в аналитической форме с использованием точек концов. Например, если A и B — концы отрезка, то он может быть обозначен как AB.

Отрезки могут использоваться в различных контекстах, например, в строительстве, инженерии или математике. Они являются важными элементами визуализации и анализа пространственных конструкций и объектов.

Применение

Лучи широко используются для моделирования световых потоков в физике и оптике. Например, они могут быть использованы для описания луча света, который распространяется от источника и падает на поверхность.

Отрезки часто применяются в геодезии, строительстве и дизайне. Например, они могут быть использованы для измерения расстояния между двумя точками на земле или для создания прямоугольной формы при проектировании здания.

Оба понятия также имеют важное значение в математических и графических приложениях. Например, лучи могут быть использованы для моделирования прямых линий на графиках, а отрезки могут быть использованы для создания геометрических фигур или сегментов на прямых линиях

Таким образом, лучи и отрезки имеют широкое применение в различных областях науки и техники, помогая нам моделировать, измерять и создавать геометрические объекты и структуры.

Луч в геометрии: определение

Игрушечный лазер в темноте. Пучок света, проходящий через небольшое отверстие. Или то, как в иллюстрациях к сказкам изображают солнышко. Все эти явления можно описать одним словом — луч.

И вновь различия…

Практика предыдущих уроков показала: сравнения между геометрией и повседневностью стоит проводить осторожно. Мы привычно смотрим на луч как на нечто, что берет начало в некоторой точке и движется в направлении другой точки

Луч в геометрии кое-чем сильно отличается. Прежде всего тем, что понятие луча абстрактно, поскольку его определение как фигуры базируется на прямой.

Давайте разберем, каким образом абстракция в виде прямой переносит ряд своих свойств на луч в геометрии. Рассмотрим еще раз чертеж с прямой $a$ и точкой $A\in{a}$.

Дополнительно отметим точки $B$, $C$ и $D$, все принадлежащие прямой $a$. Точки $B$ и $C$ располагаются по одну сторону от точки $A$, точка $D$ принадлежит другой стороне. Часть прямой, которая разбивается точкой $A$ и состоит из множества точек, включающее в том числе точки $B$ и $C$, — это луч.

Определим луч в геометрии:

Чем отличается луч от прямой?

Полуплоскость есть часть плоскости. Деление плоскости на полуплоскости выполняется прямой. Проведем параллель: луч в геометрии есть часть прямой; деление прямой на лучи выполняется точкой. Чем отличается луч от прямой? Луч в геометрии частично ограничен, если сравнивать его с прямой.

В то время как прямая простирается от бесконечности до бесконечности, луч «стартует» в некоторой точке и простирается до бесконечности.  

Прямая в геометрии	Луч в геометрии	Отрезок в геометрии
Множество точек	Множество точек части прямой	Множество точек прямой, заключенных между двумя точками
Бесконечна	Имеет точку начала и не имеет точки конца	Имеет точку начала и точку конца
Не имеет строгой направленности	Имеет направленность	Не имеет строгой направленности

Прямые, лучи, отрезки: чем в геометрии отличается луч от прямой и отрезка.

{"questions":,"items":}}}]}

Как обозначаются лучи?

Точка, разбивающая прямую на два луча, называется начальной точкой. Ее используют в качестве обозначения луча. К примеру, отметим на прямой $c$ точку $D$. Часть прямой $c$, направленную стрелкой, можно обозначить как луч $D$ — строчной латинской буквой согласно точке, являющейся для луча начальной.  

Когда говорят «луч $D$», какая часть луча имеется в виду — слева от точки или справа?

Вопросом, как обозначаются лучи с учетом направления, нам не пришлось задаваться, ведь мы определили направление с помощью чертежа. Чтобы избежать путаницы в том, как обозначаются лучи, иногда используется две точки: начальная и еще одна точка, направляющая, принадлежащая определяемому лучу.

Рассмотрим следующий пример: дана прямая $a$, точки $A$ и $B$. Так, луч $A$ также можно обозначить как луч $AB$.

Это интересно: как обозначаются лучи не у нас

В зарубежной литературе прямая и производные из нее фигуры задаются на опоре двух точек и специальных над-символов: «—», «$\rightarrow$» и «$\leftrightarrow$». Этот способ удобен тем, что не нужно по тексту доказательства или решения задачи постоянно определять словом, что имеется в виду под условным $AB$ — луч $AB$ или же отрезок $AB$.

{"questions":[{"content":"`image-1` Проверка смекалки. Догадаетесь, где здесь задана прямая, где — луч, а где — отрезок?Отрезок указан под цифрой `fill_choice-6`. Луч указан под цифрой `fill_choice-47`.Прямая указана под цифрой `fill_choice-68`.","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/07/test-question.svg"},"fill_choice-6":{"type":"fill_choice","options":,"answer":2},"fill_choice-47":{"type":"fill_choice","options":,"answer":1},"fill_choice-68":{"type":"fill_choice","options":,"answer":0}},"hints":}]}

Удобно ли? Удобно! Однако пока такой формат нотации не получил широкого распространения в нашей учебной литературе. Знать, по крайней мере, полезно, ибо встретиться подобное может где угодно. В самых неожиданных местах.

Как применять знания о лучах и отрезках в повседневной жизни?

Знание о лучах и отрезках, как об элементах геометрии, может оказаться полезным в повседневной жизни. Например, в архитектуре и строительстве, знание отрезков поможет в расчете длины стены или размеров комнаты. Определять пересечение лучей можно при проектировании систем видеонаблюдения или светофоров на дорогах.

В жизни может возникнуть необходимость сравнить длины нескольких предметов. Здесь помогут знания об отрезках. Также, знание о том, как определять угол между лучами может стать полезным при работе с геодезическими измерениями.

Таким образом, знания о лучах и отрезках не только необходимы для изучения математики, но также могут быть применены в различных сферах жизни, где требуются элементы геометрии.

Что такое отрезок?

Отрезок — это часть прямой, содержащая две точки, называемые концами отрезка. Отрезок обозначается двумя буквами, обозначающими концы отрезка и через дефис. Например, отрезок с концами A и B обозначается как AB.

Какой пример задачи можно решить с помощью отрезков?

Один из примеров задач, которую можно решить с помощью отрезков, это определение расстояния между двумя точками. Для этого нужно провести отрезок между этими двумя точками и затем измерить его длину.

Что такое луч?

Луч — это часть прямой, которая начинается в одной точке и продолжается в бесконечность. Луч обозначается двумя буквами, первая буква обозначает начальную точку, а вторая — любую другую точку луча.

Как различить отрезок и луч?

Отличия между отрезком и лучом в том, что отрезок имеет два конца, а луч имеет только одну начальную точку и продолжается в определенном направлении до бесконечности.

Как определить длину отрезка?

Длину отрезка можно определить с помощью линейки или другого измерительного инструмента. Нужно поместить начало линейки на один конец отрезка и прочертить линию до другого конца отрезка, затем измерить длину этой линии.

Как определить направление луча?

Направление луча определяется второй буквой при обозначении луча. Если вторая буква находится слева от начальной точки, то луч направлен влево, если справа — вправо.

Какую задачу можно решить с помощью луча?

Один из примеров задач, которые можно решить с помощью луча — это определение угла между двумя отрезками. Нужно нарисовать два отрезка, провести луч из одного из их общих концов и измерить угол между лучом и другим отрезком.

Отрезок

Для обозначения отрезка используется две точки с вертикальной чертой между ними, например AB. Порядок записи концов отрезка имеет значение, поэтому AB и BA — разные отрезки.

Длина отрезка может быть вычислена с использованием координат его концов. Для этого можно воспользоваться формулой длины отрезка:

|AB| = √((x₂ — x₁)2 + (y₂ — y₁)2)

где (x₁, y₁) и (x₂, y₂) — координаты концов отрезка AB.

Отрезок может быть горизонтальным, вертикальным или наклонным. Горизонтальный отрезок расположен параллельно оси X и имеет координаты (x₁, y) и (x₂, y), где x₁ ≠ x₂, и y — любое число. Вертикальный отрезок расположен параллельно оси Y и имеет координаты (x, y₁) и (x, y₂), где y₁ ≠ y₂, и x — любое число.

Отрезок является важным понятием в геометрии и находит применение в различных областях, таких как строительство, инженерия, а также в математических и компьютерных науках.

Определение отрезка

Отрезок может быть представлен на плоскости с помощью линейного графика, где точки, соответствующие концам отрезка, обозначены буквами. Например, отрезок АВ обозначает отрезок, заключенный между двуми точками А и В.

Отрезок может быть ограниченным или неограниченным. Ограниченный отрезок имеет конечные концы и заключен между ними, в то время как неограниченный отрезок продолжается бесконечно в обоих направлениях.

Отрезок является важной концепцией в геометрии и находит применение в различных областях, таких как инженерия, физика и компьютерная графика. Понимание определения отрезка и его свойств позволяет решать задачи, связанные с измерением и манипулированием прямых и отрезков

Геометрические свойства отрезка

Основные геометрические свойства отрезка включают:

Длина отрезка	Длина отрезка — это расстояние между его концами. Длину отрезка обозначают символом |AB|, где A и B — концы отрезка.
Середина отрезка	Середина отрезка — это точка, которая делит отрезок пополам. Если отрезок AB, то середину обозначают символом M, и она является точкой, для которой AM = MB.
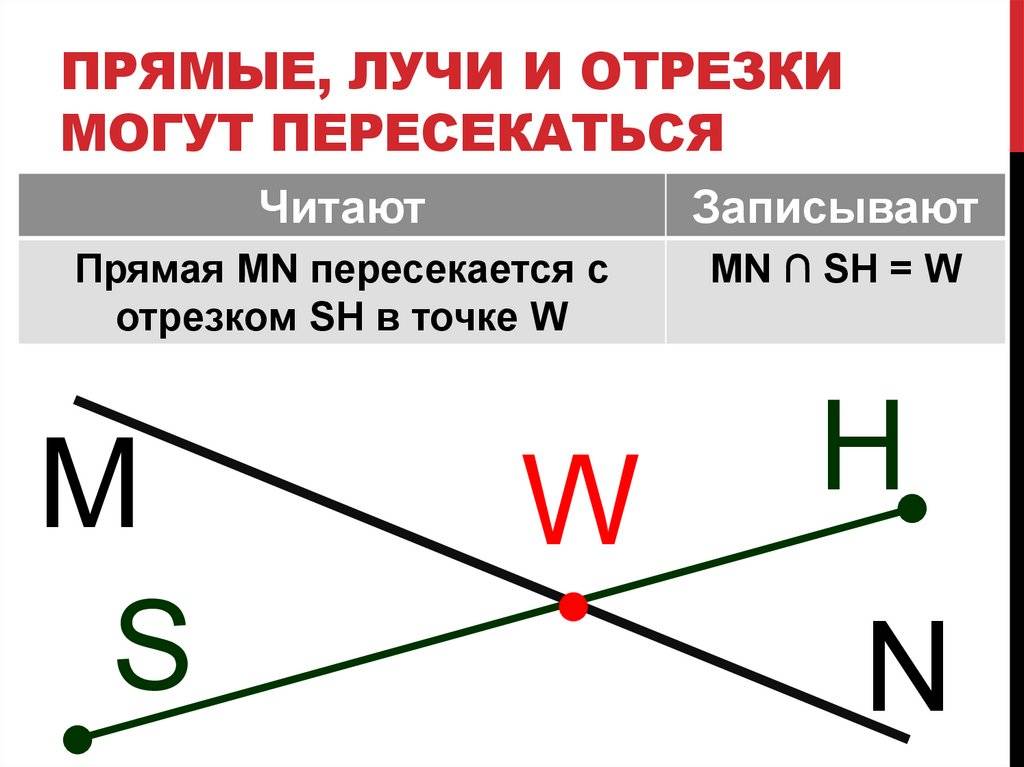
Отрезок и прямая	Отрезок может пересекать прямую в одной или двух точках. Если отрезок AB пересекает прямую в точке C, то его можно записать как AB ∩ l = C, где l — прямая.
Отрезок и окружность	Отрезок может пересекать окружность в одной или двух точках. Если отрезок AB пересекает окружность в точке C, то его можно записать как AB ∩ О = C, где О — окружность.

Знание геометрических свойств отрезка помогает в решении задач по геометрии и позволяет более точно определить пространственное расположение объектов.

Правило встречается в следующих упражнениях

Задание 34, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 54, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 286, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 417, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 814, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1167, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 4, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 10, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 17, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 2, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Принципы классификации

Так как луч является частью прямой, поэтому через любую его точку проводится множество прямых, но только через две несовпадающие проходит одна прямая. Луч можно изобразить в нескольких вариантах: пересечение, скрещивание и параллельность.

Чтобы задать луч на плоскости, используется линейное уравнение. Фигуры называются разными способами и с помощью знаков. Можно провести полупрямую «О». Её начальная точка считается исходной и другой не существует. Другой способ записи — использование нескольких букв в середине либо в иных частях линии. Если в задаче дана прямая, её можно обозначить двумя буквами, размещёнными в разных её частях, к примеру, (АB).

Третий метод обозначения: точка «О» находится с некоторым отступом от начала. Центральную часть можно назвать буквой К. В таком случае весь луч будет называться ОК. Если нужно начертить продолжение к прямой, понадобится отметить на чертеже линию и точку, которая будет считаться производной. С помощью последней фигуры делится первая на 2 линии, которые не пересекаются между собой. Чтобы обозначить продолжение, рисуется линия карандашом.

Она будет иметь общее начало с основополагающей, но не будет совпадать с ней. Из т. О проводится прямая, не располагающаяся на дополняющих, но имеющая с ними одно общее начало. На новом луче отмечается т. В. На продолжении лежит отрезок ОВ.

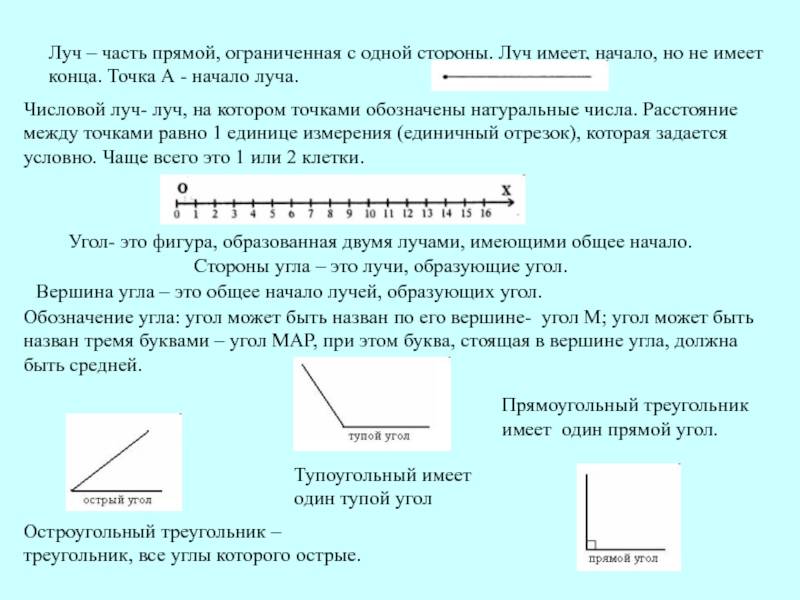
Неразвернутый угол является случаем луча. Если стороны первой фигуры представлены в виде дополнительных полупрямых одной прямой, тогда угол является развёрнутым. Его значение равняется 180 градусов. Если значение угла иное, тогда он неразвернутый.

Следует отличать геометрические лучи от световых.

В математике фигура представлена в виде линии, у которой нет ничего общего с энергией. Для световых лучей характерно несконцентрированное направление, дефракция (переломанный). Но при сильном потоке света наблюдается их чёткое направление.

Аксиомы и доказательства

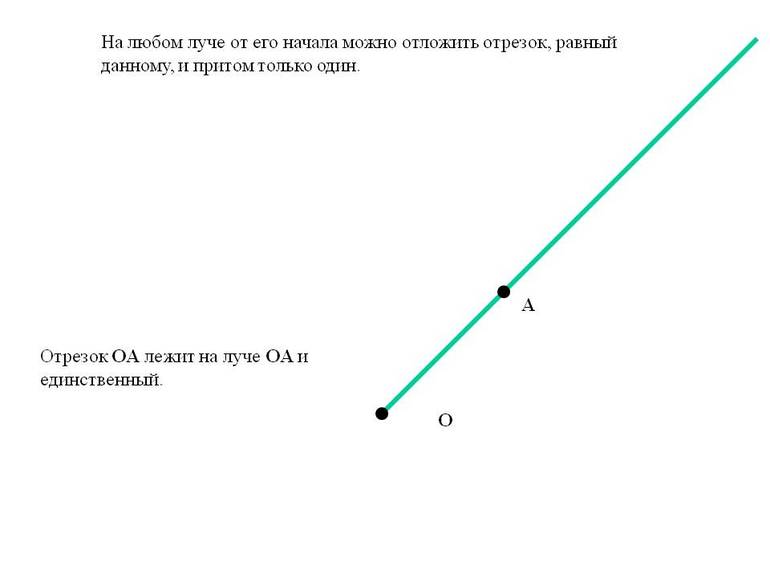
Свойства лучей определяются аксиомами. Положение 1: на любом луче от начала можно отложить отрезок определённой длины, и только один.

Доказательство: если на линии от начала А отложить 2 равных отрезка АВ и АС, тогда точки С и В совпадут. В и А не лежат на прямой, а находятся с одной стороны от неё. Если отрезок АВ не пересекает эту прямую, тогда множество точек, лежащих с единой стороны от прямой, называется полуплоскостью. При доказательстве положения 1 следует ориентироваться на определение луча.

Аксиома: прямая разделяет плоскость на 2 полуплоскости. Следствие: если D и С находятся в различных полуплоскостях от прямой а, тогда отрезок DC пересекает а. Из этого вытекает теорема: A, B, O, C расположены на прямой а таким образом, что А и В находятся с одной стороны от т. О, т. С и В — с одной стороны от О. При этом А и С размещены с одной стороны от О.

Доказательство: нужно провести через О прямую b, которая отлична от а. Она будет разбивать плоскость на 2 полуплоскости. На одной из них находится т. В. Так как отрезки BC и AB не пересекают прямую b, поэтому точки А и С находятся в одной полуплоскости с В. Отрезок АС не пересекает b. На нём не находится т. О. От неё по одну сторону размещены т. А и С.

Предположение: если O, A, B, C принадлежат прямой а, при этом А находится между В и О, тогда А лежит между О и С. По одну сторону от О находятся три точки А, B и C.

Доказательство: так как по условию т. А находится между О и В, поэтому А и В лежат по одну сторону от О. По второму условию В и С лежат по эту же сторону от О. Исходя из теоремы 1, А, В и С лежат по одну сторону от т. О.

Теорема: если O, A, B, C принадлежат одной линии а, т. А лежит между В и О, а т. В между О и С, тогда В находится между А и С.

Доказательство: выдвигается предположение, что из условия теоремы заключение не следует. Точка В не находится между А и С. По свойству взаиморасположения A, B, C, точки А и С лежат по одну сторону от В. По предположению следует, что они лежат по одну сторону от О, либо A, C, O лежат по одну сторону от B. Это противоречит условию: О и С находятся по разные стороны от В, либо А и С размещены по иную сторону от В, в отличие от т. О.

Подобное противоречит условию принадлежности А отрезку ОВ. Такое противоречие показывает, что предположение о т. В, не лежащей между А и С, неверное. Следовательно, точка В находится между А и С, что доказывает теорему. При решении геометрических задач, связанных с плоскостью и фигурами на ней, учитываются основные теоремы, доказанные учеными за всю историю математики.

Как решать задачи на определение угла между лучами?

Перед тем как решить задачу на определение угла между лучами, нужно понимать, что такое угол и как его измеряют. Угол — это фигура, которая образуется двумя лучами и точкой пересечения этих лучей, которая называется вершиной угла. Угол измеряется в градусах.

Чтобы решить задачу на определение угла между лучами, нужно знать, как найти этот угол. Для этого нужно найти точку пересечения двух лучей, а затем измерить угол между ними. Если точка пересечения лучей отсутствует, нужно найти угол между параллельными лучами.

Часто в задачах на определение угла между лучами нужно использовать знания о дополнительных и смежных углах. Дополнительные углы — это два угла, сумма которых равна 180 градусов. Смежные углы — это два угла, которые имеют общую сторону и сумма которых равна 180 градусов.

При решении задач на определение угла между лучами нужно быть внимательным и пользоваться формулами для вычисления углов. Не забывайте проверять свои ответы и пересчитывать их при необходимости.

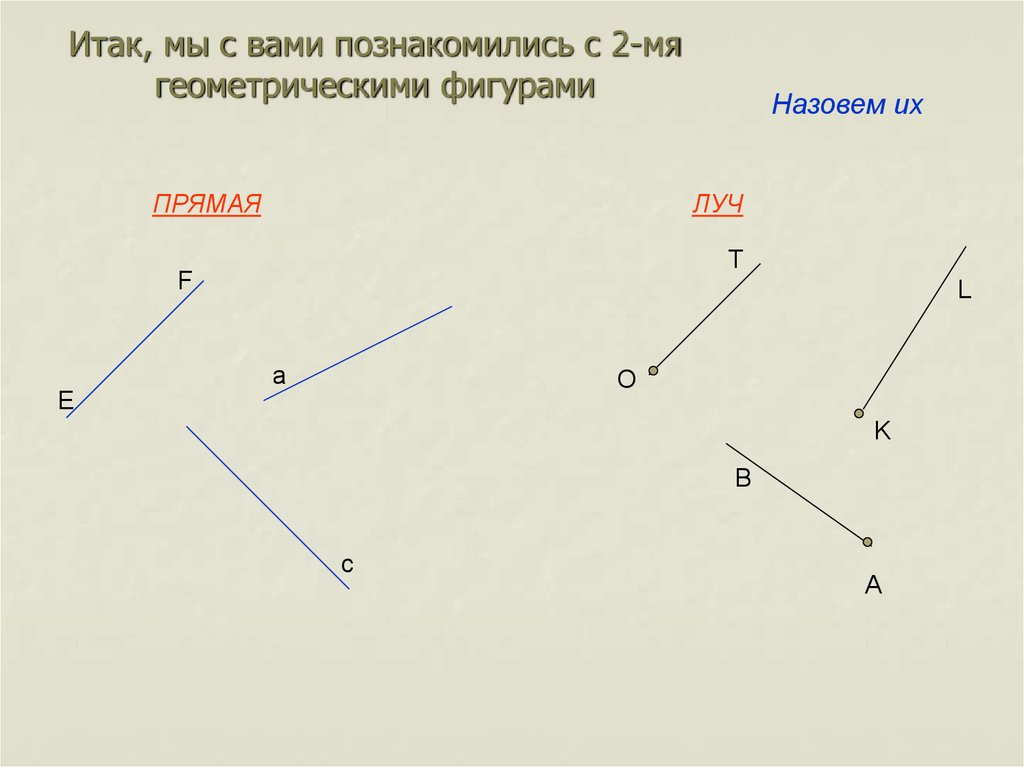
Луч — геометрическая фигура

Построим прямую АВ

(прямая обозначена двумя большими латинскими буквами, например, А и В)

Отметим на прямой АВ точку О

Точка О разбивает прямую АВ на две части (влево от точки О и вправо от точки О)

Части, на которые точка О разбивает прямую АВ, выделены цветом

Каждая из этих частей называется лучом, а точка О является началом одного и другого луча

Назовем получившиеся лучи:

Луч ОА, точка О — начало луча ОА; конца у луча ОА нет

Луч ОВ, точка О — начало луча ОВ; конца у луча ОВ нет

Луч является геометрической фигурой

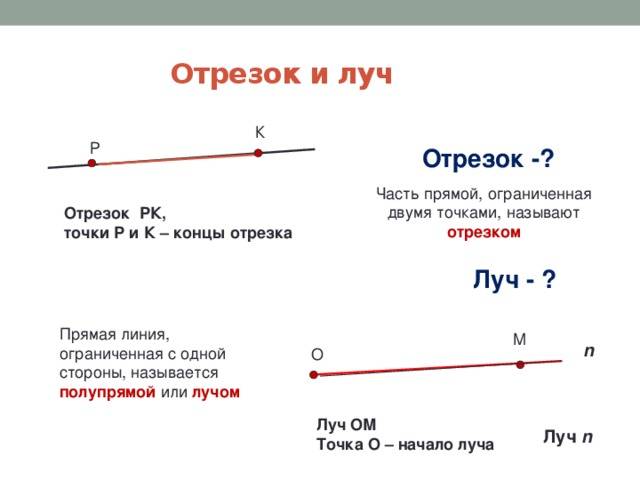
Луч — это часть прямой, ограниченная с одной стороны

Луч имеет начало, но не имеет конца

Другой способ обозначений

(прямая обозначена малой латинской буквой, например, m)

Точка О разбивает прямую m на два луча

Чтобы лучи обозначить, отметим на прямой m дополнительно произвольным образом две точки — А и В

Луч ОА, точка О — начало луча ОА; конца у луча ОА нет; точка А принадлежит лучу ОА;

Луч ОВ, точка О — начало луча ОВ; конца у луча ОВ нет; точка В принадлежит лучу ОВ;

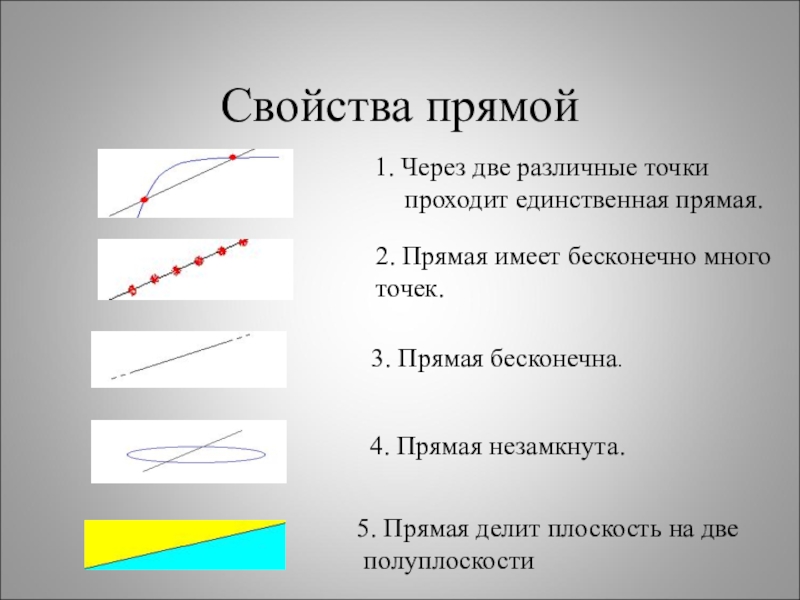
Свойства прямой

Прямая обладает несколькими важными свойствами:

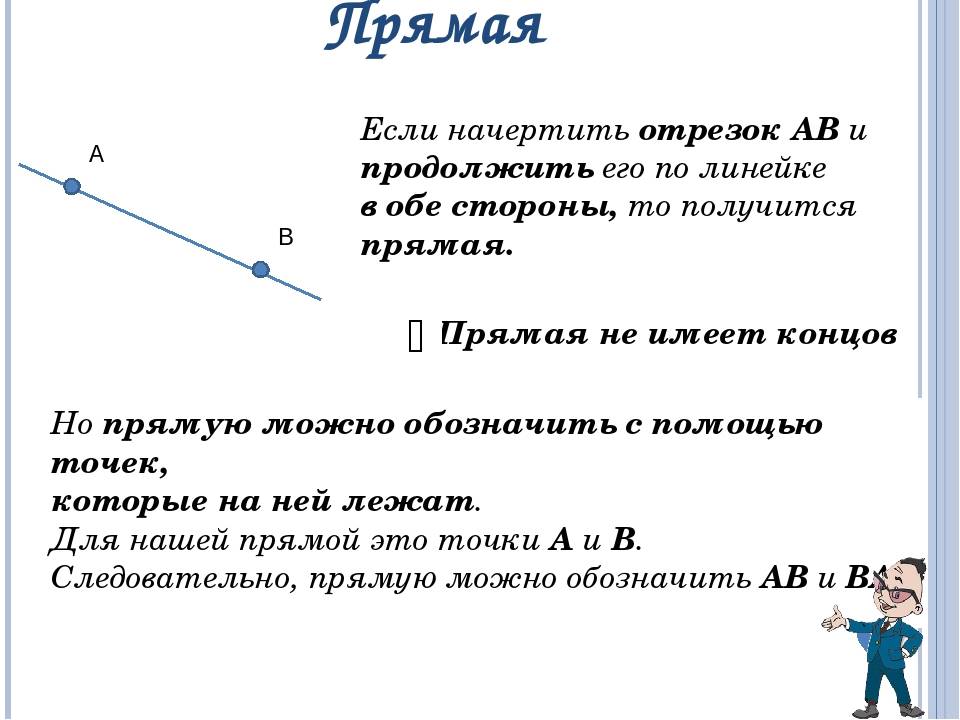
1. Прямая имеет бесконечную длину: Прямая не имеет начала и конца, она расширяется в обе стороны до бесконечности. При рисовании прямой на бумаге мы обозначаем только ее конечный участок.

2. Прямая состоит из бесконечного количества точек: Каждая точка на прямой обладает своими координатами. Все эти точки лежат на одной прямой линии и упорядочены в соответствии с выбранными измерениями.

3. Любые две точки на прямой определяют ее: Для определения прямой достаточно знать координаты любых двух ее точек. Весьма интересно, что если известны две точки на прямой, то на ней уже можно построить точно одну прямую, которая проходит через эти точки.

4. Прямая не имеет ширины: Прямая — это нулевая размерность, она не имеет ширины и представляет собой одномерный объект. Это делает прямую различной от отрезка, который имеет конечную длину.

Эти свойства прямой помогают в изучении ее геометрических особенностей и используются в различных областях науки и техники.

Луч может быть описан именем его начальной точки и направлением, в котором он стремится.

Свойства луча

У луча есть несколько важных свойств:

1. Начальная точка: каждый луч имеет начальную точку, от которой он начинается и которая определяет его положение на прямой.
2. Направление: луч расширяется только в одном направлении и продолжается бесконечно в этом направлении.
3. Бесконечность: луч не имеет конца, он продолжается бесконечно в одном направлении.
4. Множество точек: луч состоит из бесконечного количества точек, которые находятся с одной стороны от начальной точки и продолжаются в направлении луча.
5. Угол: луч можно использовать для определения углов в геометрии.

Свойства луча делают его полезным в различных математических и геометрических задачах. Лучи используются для строительства углов, измерения и определения положения объектов на плоскости.

Определение отрезка

Отрезок обозначается двумя точками, между которыми находится соответствующий отрезок прямой. Например, если на прямой AB находится точка C, то отрезок AC обозначается как AC или CA, в зависимости от порядка записи точек.

Отрезок отличается от прямой и луча тем, что у него есть начальная и конечная точка, в то время как прямая бесконечна в обе стороны, а луч имеет только одну начальную точку и протяженность в одну сторону.

Свойства отрезка:

• Длина отрезка: длина отрезка — это расстояние между его начальной и конечной точкой. Она может быть вычислена с использованием формулы расстояния между двумя точками в декартовой системе координат.
• Симметричность: отрезок является симметричным относительно середины. Это означает, что если точка D является серединой отрезка AC, то отрезок AD имеет ту же длину и направление, что и отрезок DC.
• Сумма длин: сумма длин двух отрезков равна длине нового отрезка, который можно получить путем соединения конечной точки одного отрезка с начальной точкой другого.

Отрезки широко используются в геометрии и других областях математики для изучения и анализа положения объектов и их взаимосвязи.

Когда использовать прямую луч и отрезок?

Отрезок — это часть прямой между двумя точками. Он имеет начало и конец, т.е. конечные точки. Отрезок обладает определенной длиной, которая вычисляется как расстояние между его конечными точками. Отрезок может быть использован, когда необходимо задать конкретное расстояние между точками или обозначить границу между двумя объектами.

Прямая же является бесконечной линией, не имеющей начала и конца. Она продолжается в бесконечность в обоих направлениях

Прямая используется, когда не требуется указывать конкретные границы и точки, а важно описать направление или общее расположение объектов

Луч — это часть прямой, имеющая начало, но не имеющая конца. Она распространяется от начальной точки в определенном направлении. Луч используется, когда необходимо указать направление или показать, что объект расположен в определенной части пространства.

Таким образом, использование отрезка, прямой или луча зависит от задачи, которую необходимо решить в геометрии. Отрезок используется для определения конкретного расстояния или границы, прямая — для указания направления или общего расположения, а луч — для показа направления или местоположения в пространстве.

Применение прямого луча

• Расстояние: Прямой луч может быть использован для измерения расстояния между двумя точками на прямой. Для этого необходимо отложить на луче от точки измерения нужное расстояние и удалиться в противоположном направлении до встречи с прямой или другим объектом.
• Направление: Прямой луч указывает на направление движения или расположения объекта. Например, при ориентировании на карте можно использовать прямой луч для указания вектора движения от одной точки к другой.
• Отрезать: Прямой луч может быть использован для отрезания или разделения пространства на две части. Например, чтобы разделить плоскость на два полутора покрытых прямолинейными фигурами, можно провести прямой луч, который будет служить границей разделения.

В целом, применение прямого луча в геометрии позволяет решать множество задач, связанных с измерением расстояний, определением направления и разделением пространства. Этот геометрический объект играет важную роль в понимании и визуализации различных феноменов в геометрии и других областях науки.

Применение отрезка

В геометрии, отрезок используется для определения расстояния между двумя точками. Он является более конкретным понятием, чем прямая или луч, потому что имеет фиксированную длину. Расстояние между двумя точками на плоскости может быть выражено как длина отрезка, соединяющего эти точки.

Отрезок также является важным понятием в физике. Например, вектор скорости может быть представлен в виде отрезка, указывающего направление и величину движения тела. Отрезок также используется в описании других векторных величин, таких как сила, импульс и момент силы.

В отличие от луча, отрезок имеет конечную длину и не простирается до бесконечности. Он имеет точно определенные начало и конец, и может быть визуализирован как отрезок на плоскости или в пространстве.

Отрезок также может быть использован для определения направления в пространстве. Его направление определяется вектором, который начинается в начале отрезка и указывает к его концу. Вектор отрезка позволяет определить перемещение и изменение позиции объекта в пространстве.

«Начальные геометрические понятия»

Ключевые слова конспекта: начальные геометрические понятия, математические утверждения в геометрии, аксиома, определение, теорема, доказательство, точка, прямая, линия, плоскость, луч, отрезок, длина отрезка, измерение отрезков, единицы длины, расстояние между двумя точками.

Математические утверждения в геометрии

Аксиома – это утверждение, принимающееся как истинное без доказательства. Слово «аксиома» происходит от греческого слова «аксиос» и означает «утверждение, не вызывающее сомнений».

Определение – четкое формулирование того или иного математического понятия.

Теорема – математическое утверждение, истинность которого устанавливают путем доказательства.

Признак – утверждение,которое позволяет доказать, что данная фигура является фигурой, которая имеет данные качества или связана необходимыми отношениями.

Доказательство – размышление, в ходе которого устанавливается истинность или ложность утверждения.

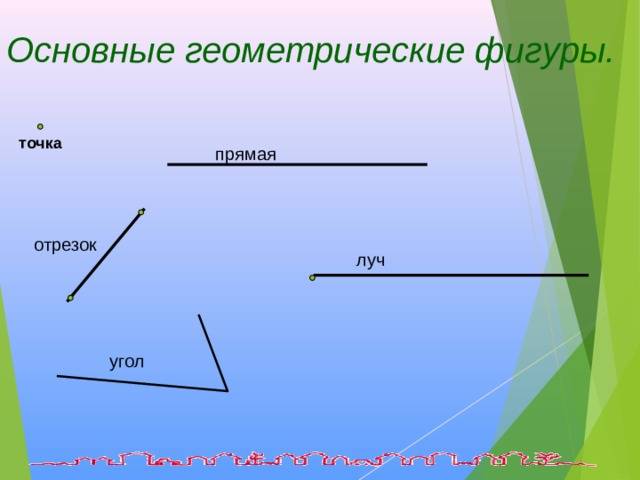
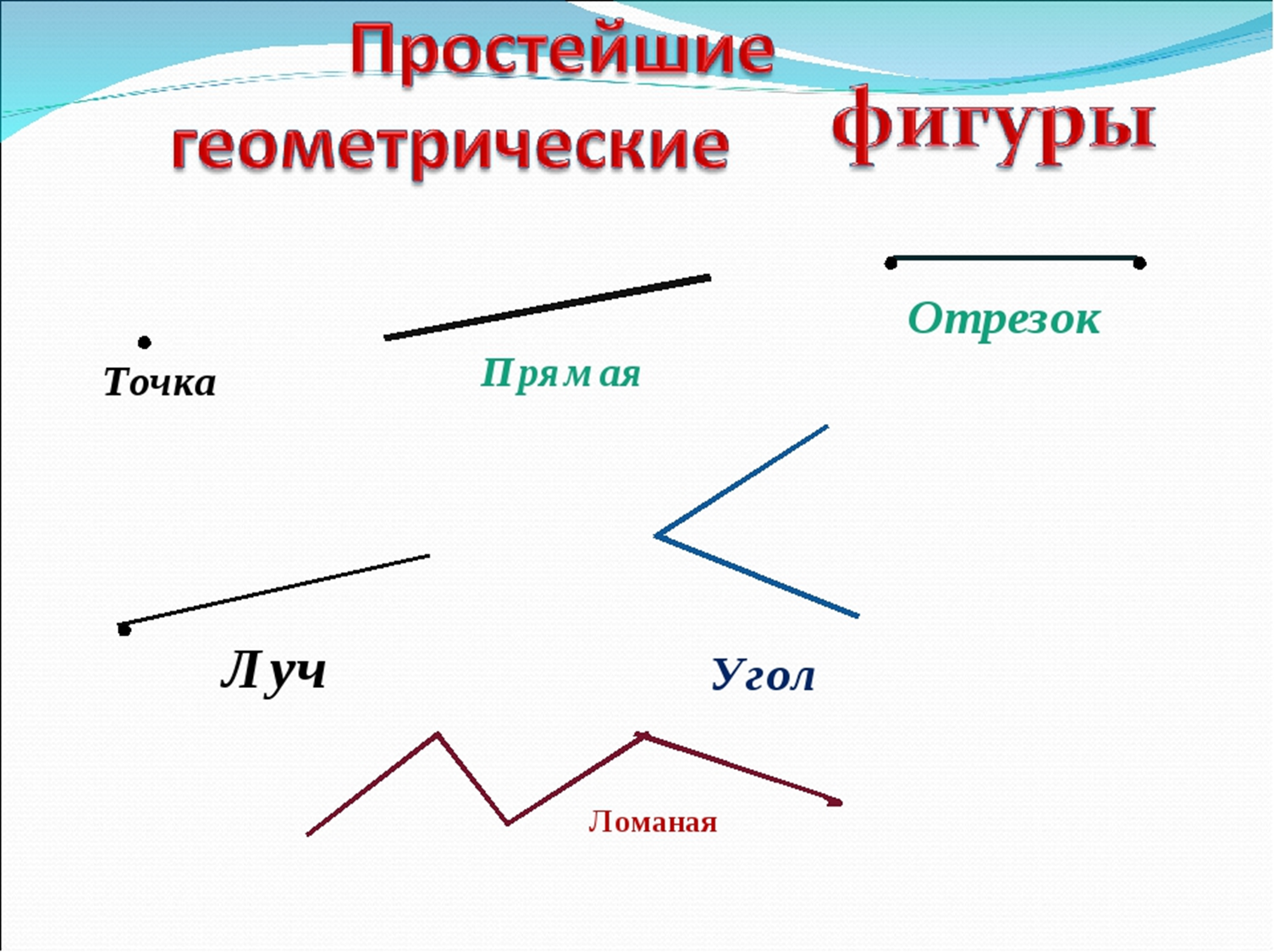
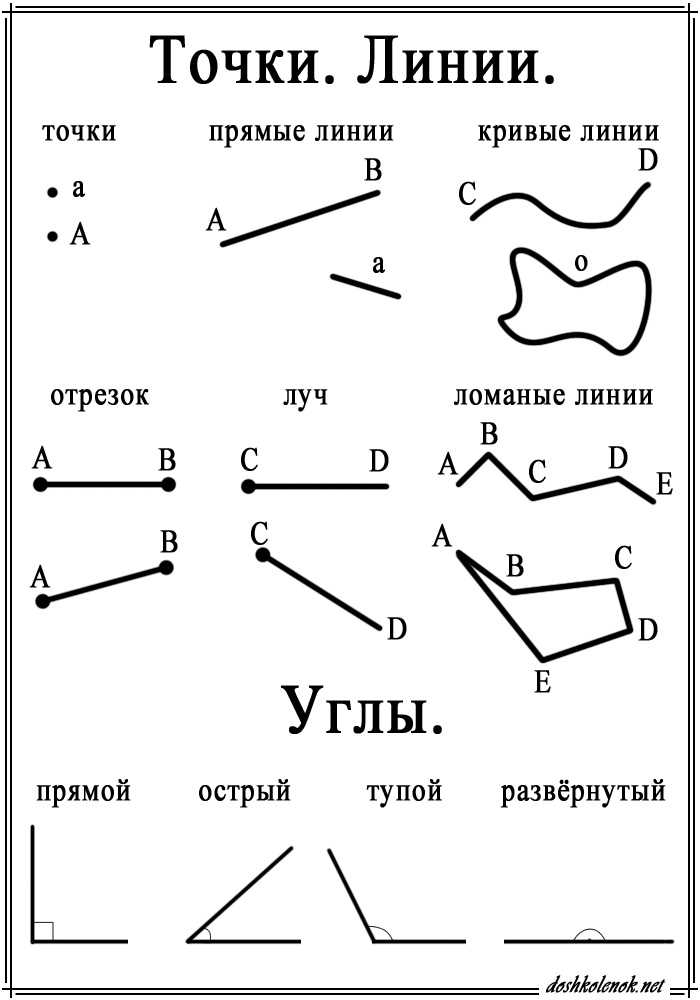
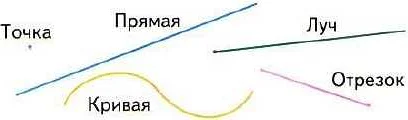
Простейшие геометрические фигуры

Точка — понятие, не имеющее значения. Представление о точке дает след на листе бумаги, сделанный хорошо заостренным карандашом. Слово «точка» является переводом латинского слова «pungo», что означает «тыкаю», «дотрагиваюсь». Обозначают точки большими латинскими буквами: А, В, С.

Прямая — понятие, не имеющее значения. Представление о прямой дают: туго натянутая нитка; луч света, проходящий сквозь узкое отверстие. Обозначают прямые латинскими буквами: а, b, … или двумя большими латинскими буквами: АС, ВС, … Прямая бесконечна.

Слово «линия» происходит от латинского слова «tinea», что значит «лён», «льняная нить», иногда это слово понимают как «прямая линия», и отсюда происходит слово «линейка».

Плоскость — понятие, не имеющее значения. Представление о плоскости дают: поверхность стола, оконного стекла, поверхность озера в тихую погоду и т.п. Плоскость предcтавляют неограниченной, идеально ровной и гладкой. Обозначают плоскости маленькими греческими буквами:  α, β, …

Луч (полупрямая) — часть прямой, состоящая из всех точек этой прямой, которая лежит по одну сторону от данной на ней точки (начало луча).

Отрезок и его длина

Отрезок — часть прямой, ограниченная двумя точками, включая эти точки. Равные отрезки — отрезки,которые совпадают при наложении. Середина отрезка — точка, которая делит отрезок пополам.

Расстояние между двумя точками

Расстояние между разными точками — длина отрезка с концами в данных точках. Расстояние между точками, которые совпадают, равно .

Для любых точек А и В расстояние от А до В равно расстоянию от В до А. Для любых трех точек расстояние между двумя из них не больше суммы двух других расстояний.

Это конспект по теме «Начальные геометрические понятия». Выберите дальнейшие действия:

• Перейти к следующему конспекту: Аксиомы планиметрии
• Вернуться к Списку конспектов по геометрии