Чем отличаются позиционные системы счисления от непозиционных?

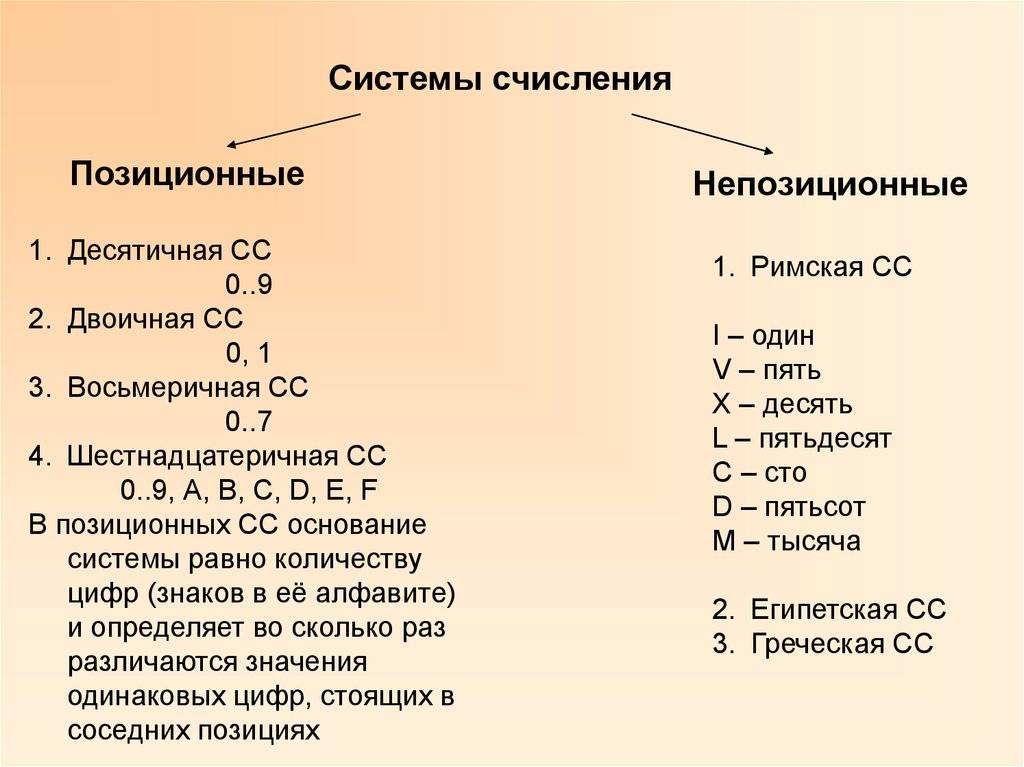
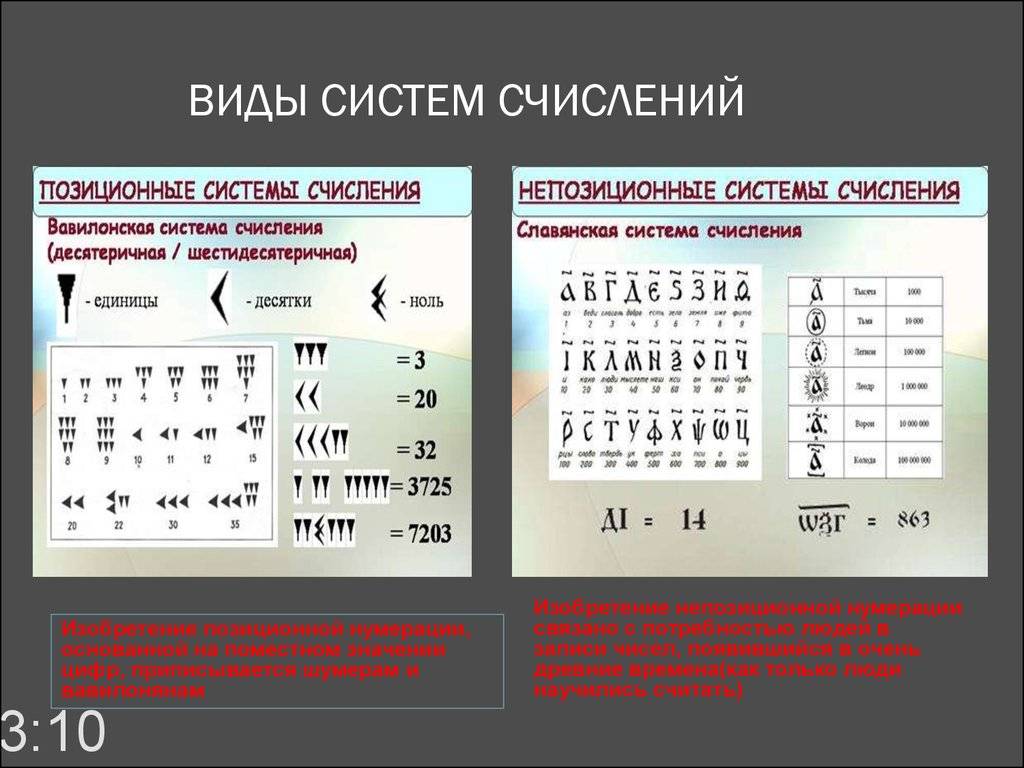
Введение

На заре зарождения человеческого общества понятия счёта практически не существовало. Люди могли отличить два предмета от трёх, но всё что было больше этого скрывалось за термином «много». Как правило, при подсчёте чего-либо количество предметов соотносилось с количеством пальцев на конечностях.

Постепенный прогресс нашего общества сделал счёт насущной потребностью. Сначала изображение натуральных чисел сводилось к написанию чёрточек, но впоследствии для этих целей начали применяться буквенные обозначения и символы. Жители древнего Новгорода применяли славянский алфавит, для написания чисел над славянскими буквами ставили знак ~ (титло).

Получи помощь с рефератом от ИИ-шки

ИИ ответит за 2 минуты

В Древнем Риме зародилась методика, которая известна и сегодня как римская система нумерации. В ней числовые значения представляются буквами латинского алфавита. Сегодня её используют для нумерации глав в книгах и тому подобного. Вот список римских цифр: I = 1; V = 5; X = 10; L = 50; С = 100; D = 500; M = 1000. В римской системе нумерации прослеживаются отголоски пятеричной системы счисления. Арифметические операции над большими числами в римской системе достаточно трудоёмки, но она применялась в Италии вплоть до тринадцатого века, а в некоторых европейских государствах аж до шестнадцатого века.

Славяне для обозначения чисел применяли весь алфавит, но с незначительными отклонениями от порядка следования букв в алфавите. Разные буквы обозначали разное число единиц, десятков и сотен. Такая система имела две существенные проблемы, которые и вызвали отказ от неё. Это слишком большое количество разных знаков, в частности для отображения большого числа, и, что ещё хуже, очень было неудобно выполнять арифметические операции.

Наиболее совершенной и доступной стала общеизвестная сегодня десятичная система счисления, которая зародилась в Индии, усовершенствована арабами и уже потом появилась в европейских странах. В качестве основания десятичной системы выбрано число десять. Конечно, существуют системы счисления, имеющие различные основания. Жители древнего Вавилона применяли шестидесятеричную систему счисления. Её отголоски видны и в наше время, поскольку мы и сегодня считаем, что в часе 60 минут, а в минуте 60 секунд. В древние времена люди так же пользовались двенадцатеричной системой. Сегодня от неё осталась широко известная «дюжина», то есть число двенадцать. Ещё существует обычай подсчитывать количество некоторых предметов не числом десятков, а числом дюжин, к примеру, это столовые приборы.

Таблица соответствия чисел систем счисления

система» data-order=»Двоичный система» стиль = «минимальная ширина: 24,6711%»; ширина:24,6711%;»>Двоичный система	система» data-order=»восьмеричный система» стиль = «минимальная ширина: 24,1776%»; ширина:24,1776%;»>восьмеричная система	система» data-order=»Десятичный система» стиль = «минимальная ширина: 22,2039%; ширина:22,2039%;»>Десятичный система	система» data-order=»Шестнадцатеричный система» стиль = «минимальная ширина: 28,9474%»; ширина:28,9474%;»>Шестнадцатеричный система
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	1
11	1011	1. 3	Б
12	1100	14	С
1. 3	1101	15	Д
14	1110	16	Е
15	1111	17	Ф
16	10 000	20	10
17	10001	21	11
18	10010	22	12
19	10011	23	1. 3
20	10100	24	14
21	10101	25	15
22	10110	26	16
23	10111	27	17
24	11000	30	18
25	11001	31	19
26	11010	32	1А
27	11011	33	1Б
28	11100	34	1С
29	11101	35	1D
30	11110	36	1Э
31	11111	37	1эт
32	100 000	40	20

О преобразованиях

Работая с любой систе мой счисления, нужно понимать, как переводить число из одного «варианта» в другой. Эти навыки пригодятся каждому, кто планирует углубляться в IT.

В десятичную

Первый вариант – это любую «систему» привести к «десятичному виду». Тому, что привычен каждому пользователю.

Пусть будет дано число a₁a₂a₃, где основание – это b. Тогда нужно каждый разряд умножить на bn. N выступит номером разряда. Формула перевода окажется: (a₁a₂a₃)_b=(a₁*b2+a₂*b1+a₃*b)₁₀.

Из десятичной

Из десятичной системы счисления можно преобразовать число в любую другую. Здесь стоит разделить процесс на формирование дробной и целой частей. Иначе добиться желаемого результата не получится.

В случае с целой частью действовать необходимо так:

1. Последовательно выполняется деление целой части на основание новой системы. Делается это до тех пор, пока число не станет нулем.
2. Полученные остатки – это цифры искомого компонента.
3. Запись осуществляется с последнего остатка до первого.

Дробная часть преобразуется так:

1. Соответствующий элемент умножается на основание системы, в которую осуществляется перевод.
2. Целая часть отделяется.
3. Умножить дробную часть на основание новой. Делать это до тех пор, пока она не будет равна 0.
4. Записать полученный результат умножения. Делается это в порядке, соответствующем получению.

Пример – 1510 при переводе в восьмеричную систему счисления – это 17₈. Получилось как: 15/8 = 1, остаток – 7, а также 1/8 = 0, остаток 1.

Из двоичной в восьмеричную и шестнадцатеричную

Для того, чтобы перевести 1 a (число) из двоичной в 8-ю систему, нужно:

1. Разбить его на группы по 3 компонента справа-налево.
2. Недостающие разряды дополнить ведущими нулями.
3. Преобразовать каждую группу при помощи умножения разряда на 2n.

Аналогично действовать нужно с шестнадцатеричной системой, но делить компонент необходимо на группы по 4 элемента.

Из 8-ой и 16-ой в 2-ю

В случае с восьмеричной системой – каждый разряд числа преобразуется в 3-х разрядное двоичное путем деления на 2. Недостающие крайние разряды – это нули.

Шестнадцатеричная система предусматривает преобразование каждого разряда в двоичное 4-х компонентное. Сопровождается делением на 2. Недостающие крайние разряды – это нули.

Примеры использования и значимость

Исторические примеры позиционных и непозиционных систем

Изучение исторических примеров позиционных систем например, Архимедова или Вавилонская, показывает, как при их помощи древние цивилизации достигали значительного прогресса в астрономии и математике. С другой стороны, римские цифры, представляющие собой классический пример непозиционной системы, до сих пор используются для некоторых традиционных целей, таких как часы.

Влияние на современную науку и технологии

Понимание и применение позиционных систем сыграли решающую роль в развитии таких областей, как компьютерная инженерия и цифровая связь. Непозиционные системы оказали влияние в области криптографии, где они используются для создания разнообразных шифров и кодов.

Основные позиционные СС, правила перевода

Двоичная система счисления

Систему, на которой основывается работа компьютеров, придумал гениальный немецкий ученый Г.В. Лейбниц (еще до 19 века!). Он придумал и описал СС, в которой все вычисления проводятся при помощи двух простейших символов – 0 и 1.

Компьютер, как механическое устройство, получает команды в виде двоичной кодировки. Он не в силах понять сложные задания, человеческую речь, музыку или тысячи оттенков, а переводя/кодируя всю необходимую информацию при помощи 0 и 1 (сеть, отсутствие сети), можно передать ему любые команды или информацию. Естественно, такие задания выглядят как огромные массивы двух знаков.

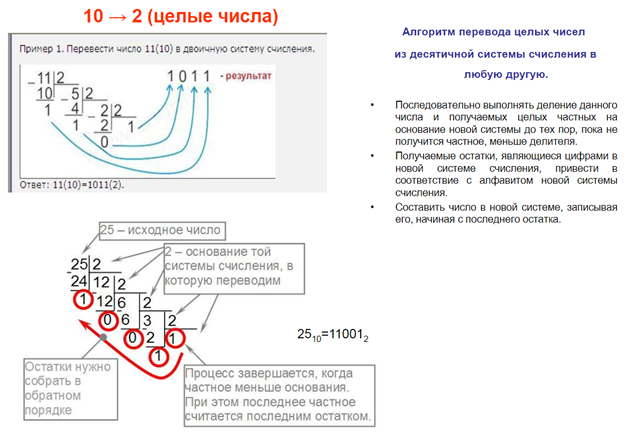
Алгоритм перевода чисел из десятичной в двоичную систему:

1. Деление на основу СС до тех пор, пока не останется в остатке значение меньше значения основы.
2. Записать остатки, от последнего к первому.
3. Первый ноль можно не писать.

111 0100 1100₂ 

Этот порядок действия позволят переводить в любую позиционную СС. В данном случае, основа – 2, остаток < или равен =.

Обратный алгоритм перевода из двоичной в десятичную систему счисления:

Записать число развернуто, то есть, сколько сотен, десятков и единиц в нем, но учитывая основу – 2

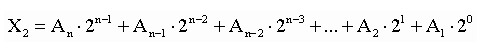
Объяснение. Развернутая форма записи 579: 5*102+7*101+9*10= 579₁₀.

Обычно мы пользуемся свернутой формой записи чисел, то есть без разбивки на разряды и умножения на основу.

1. Умножить и суммировать полученные значения.

А чтобы было легче, пользуются готовой таблицей степеней 2.

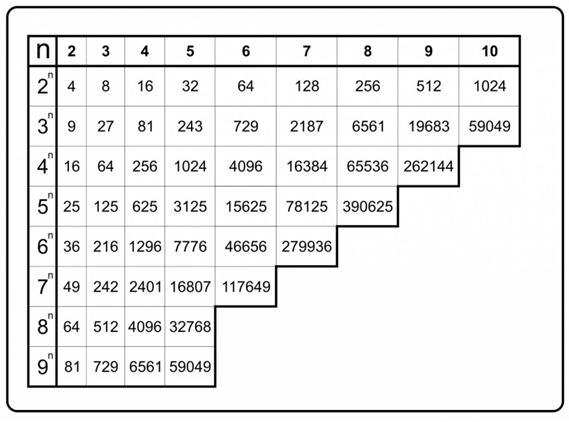
Альтернативный способ преобразования для гуманитариев

Для начала нужно написать степени двойки, начиная с самой большой:

Далее нужно отнимать от числа максимальную степень двойки и напротив нее ставить 1, если есть в исходном варианте или 0, если его нет. Перевод числа 579

Обратно еще проще. Подсчитать количество знаков – это будет степень 2 в степени -1. И так далее. А проще при помощи той же таблицы:

Если же оно на 1 больше, то число будет начинаться и заканчиваться на 1, а внутри – сплошные 0.

Восьмеричная СС

Основой такой системы является 8, а числа восьмеричной системы 0-7. Данная система счисления является позиционной и целочисленной. Применяется в сферах, связанных с цифровыми технологиями, особенно в Linux-программном обеспечении (права доступа, исполнения).

Пример: Перевести 579₈ из десятичной в восьмеричную систему счисления:

Обратный перевод из восьмеричной СС в десятичную:

1103₈ = 1∙83+1∙82+0∙81+3∙8 = 512+64+0+3 = 579₁₀

Таблица степеней

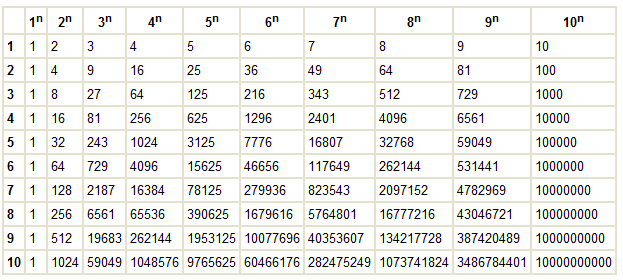
Альтернативный вариант таблицы степеней 

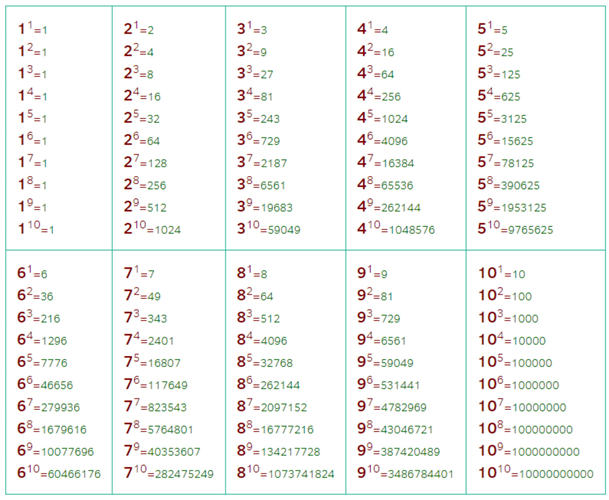
Восьмеричная и шестнадцатеричная системы счислений

Компьютерам очень удобно оперировать двоичными числами, но люди не привыкли работать с большим количеством цифр. Например, чтобы представить в двоичном виде число 1234 потребуется больше 10 двоичных цифр (10011010010). Поэтому были придуманы восьмеричная и шестнадцатеричная системы счислений. Они удобны как и десятичные числа тем, что для представления числа требуется меньшее количество разрядов. А по сравнению с десятичными числами, перевод в двоичное представление очень простой. Это как будто мы двоичное число разбили на группы по три или четыре разряда и каждой двоичной комбинации придумали значок. Вот таблица для восьмеричных цифр:

Двоичная комбинация	Значок
000
001	1
010	2
011	3
100	4
101	5
110	6
111	7

А вот таблица для шестнадцатеричных цифр:

Двоичная комбинация	Значок
0000
0001	1
0010	2
0011	3
0100	4
0101	5
0110	6
0111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

Перевод произвести очень просто, посмотрим на примере числа 010011010010.

Разбиваем его на группы по три цифры: 010 011 010 010. И по таблице переводим: 23228{\displaystyle 2322_{8}}.

Чтобы перевести число в шестнадцатеричное представление разбиваем двоичное число на группы по четыре цифры: 0100 1101 0010. И по таблице переводим: 4D216{\displaystyle 4D2_{16}}. С помощью калькулятора Windows мы можем убедиться, что всё проделано верно.

В программистских кругах шестнадцатеричные числа принято предварять значком 0x (например, 0x4D2), такое написание пошло от языка программирования C, либо значком $ (например, $4D2), такая нотация произошла от языка программирования Pascal. Иногда в литературе используют буквы «h» (от англ. hexadecimal) и «b» (от англ. binary) для обозначения соответственно шестнадцатеричных и двоичных чисел (например, FFh или 1011b).

Достоинства позиционной системы

Простое выполнение подсчета

У всех позиционных систем одни и те же алгоритмы выполнения арифметических действий. Также в позиционных системах удобно работать с дробями и отрицательными числами, которые зачастую просто невозможно представить в непозиционных системах.

Главные свойства позиционных систем:

• основание всегда записывается внутри системы как 10 (утверждение неприменимо к унарной системе счисления);
• числа можно сравнивать поразрядно, дополнив ведущими нулями до равной длины;
• сложение и вычитание можно выполнять, зная только таблицу сложения однозначных чисел.

Малое количество символов в записи

Позиционные системы используют только десять арабских цифр. Системы с основанием больше десяти добавляют к цифрам 26 латинских букв. В некоторых системах используют круглые и квадратные скобки.

Чем больше основание системы счисления, тем меньшее количество цифр понадобится для записи числа. Числа, состоящие из трех разрядов в десятичной системе, могут иметь всего два разряда в шестнадцатеричной.

Определение

Система счисления – это специальная система записи для выражения чисел. Математическое представление чисел заданного набора с использованием цифр и иных символов согласованным образом.

Совокупность правил записи чисел через символьно-цифирные конечные наборы. Одна и та же последовательность может быть представлена разными числами в различных системах «записи». Пример – 11 в десятичной системе, три – в двоичной, два – в унарной.

Значения и их особенности

Значение – это число, которое представляет та или иная цифра. Не все рассматриваемые компоненты могут работать со всеми числами, используемыми сегодня. Примеры – римские «значения». У них нет нуля.

Рассматриваемым компонент:

• представляет полезный набор чисел (примеры – целые, рациональные);
• дает уникальное представление каждому имеющемуся элементу;
• отражает алгебраические или арифметические структуры.

Без систем невозможна работа с компьютерами. Именно поэтому соответствующее направление требует отдельного внимания.

Непозиционные СС, их особенности

Первоначально древние люди ставили отметки (черточки-зарубки, точки), чтобы обозначить количество того или иного предмета. Отклики этого подхода все еще встречаются (полоски у военных, счетные палочки).

Постепенно от единиц они переходили к группам предметов по 3, 5, 10 единиц. Постепенно такие группы стали обозначаться определенными символами, что позволило сократить размер записи.

Римская СС

В ней определенным цифрам отвечают латинские буквы. Их сумма и будет числом.

Основные рекомендации при пользовании римскими цифрами:

1. Символы следует писать по убыванию слева направо.
2. Нежелательно записывать подряд более 3 одинаковых знаков.
3. Положение цифры обозначает, какой ее вклад – отрицательный, если она стоит слева от большего числа, положительный – справа.

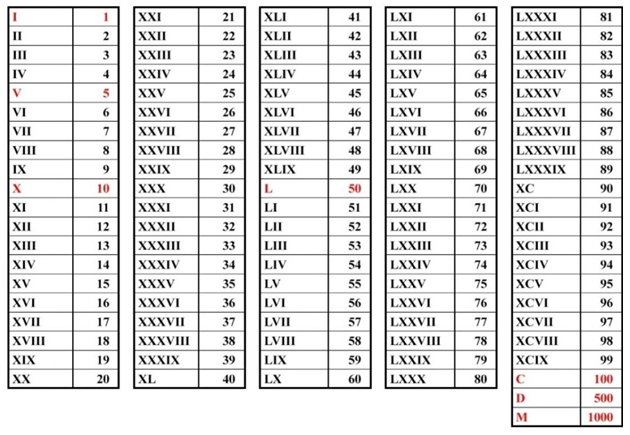Таблица римских цифр 

Недостаток этой СС в том, что для больших чисел недоступны операции сложения или другие, ещё она сложная и громоздкая. Зато римские цифры отлично вписались там, где нужна нумерация и эстетика: циферблаты, номера глав, списки, серии документов.

Двоичная

Двоичную систему счисления в основном используют устройства и компьютеры. Такое решение пришло из-за того, что 10-я требовала раньше огромных затрат. Это сказывалось на стоимости ЭВМ.

Пришлось создавать «урезанную» версию. Основание здесь – 2. Для записи используются символы:

• 0;
• 1.

Каждый разряд имеет только одно соответствующее значение. Пример 101. Это – десятичное 5. Для того, чтобы осуществить перевод из двоичной в 10-ю, требуется умножить цифру 2-го числа на 2. Возвести «двойку» в степень, равную разряду. Так 101₂ будет:

• 1*22;
• 0*21;
• 1*2.

Получится: 4+0+1=5₁₀.

Для работы с кодами ЭВМ хранит для каждой отдельной цифры триггер. Это – электронная схема, принимающая два состояния. Одно – соответствует «нулю», другое – «единице».

Для того, чтобы запомнить отдельное число, применяется регистр – группа триггеров, количество которых соответствует количество разрядов в двоичном числе. А их совокупность – это оперативная память. Число, которое содержится в регистре, носит название машинного слова. Для получения доступа их нумеруют. Номер – адрес ячейки.

Классификация позиционных систем

Двоичные

Определение

Двоичная система —  система счисления, в которой в качестве базовых чисел выбираются степени числа два.

Чтобы не путать их с числами, записанными в десятичной системе счисления, справа внизу указывают основание системы счисления. Обычно число при этом заключают в скобки.

Двоичную систему использовали задолго до возникновения информационных технологий. Во втором тысячелетии до нашей эры народы Южной Америки кодировали двоичной системой свои записи, в том числе и не числовые. Узелок и ровный участок нити чередовались друг с другом.

В современной двоичной системе, на основе которой был создан телеграф, а позже — реле и переключатели, единица обозначает наличие сигнала, ноль — его отсутствие. Цифровые электронные схемы работают по тому же принципу. Также на нем основаны сигнальные системы, использующиеся до сих пор, например, азбука Морзе.

Восьмеричные

Когда-то два индейских племени решили, что им удобно при счете смотреть на восемь промежутков между пальцами, а не на сами пальцы. Восьмеричная система счисления отразилась в их языках, в которых только восемь слов, обозначающих цифры.
В двадцатом веке, когда для написания программ требовалось зашифровывать все больше информации в двоичной системе и упростить вычисления для людей, придумали альтернативную систему, которая позволила сократить количество цифр в коде. Число восемь — это два в кубе, поэтому перевести записи из двоичной системы в восьмеричную и обратно проще, чем в десятичную.

Десятичные

Элементы числовой базы, или ключевые числа, в десятичной системе счисления представляют собой степени десяти: 10 = 10^1, 100 = 10^2, 1000 = 10^3.
В системе всего десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Число 10 — основание системы счисления. Цифры от 0 до 9 представляют собой коэффициенты разложения числа по степеням десяти.

Родиной десятичной системы счисления считается Индия, хотя еще в вавилонской цивилизации с ее шестидесятеричной системой использовались закодированные десятичные цифры, а инки в своей узелковой письменности кодировали информацию десятью цветами. Но именно в Индии начали строго соблюдать порядок разрядов числа при записи и ставить ноль, чтобы избежать путаницы. Примерно в середине VIII века эту систему стали использовать другие страны. В Европе она распространилась к XVI веку и была названа «арабской».

Шестнадцатеричные

Шестнадцатеричные системы, как и восьмеричные, появились для упрощения взаимодействия с компьютером. Кроме арабских цифр, в них используются еще и латинские буквы от А до F. В разных языках программирования для записи чисел в шестнадцатеричной системе разные правила, называемые синтаксисом.

Пятеричная

Система, связанная с количеством пальцев на одной руке, использовалась в Китае и у некоторых племен Африки. В китайском языке у иероглифов, обозначающих цифры от шести до девяти, был один и тот же знак в начале — сокращенное обозначение цифры пять. Для записи чисел в этой системе используются цифры 0, 1, 2, 3, 4.

Двенадцатеричная

Если большим пальцем руки сосчитать число фаланг на других пальцах этой руки, получится двенадцать. Группы по двенадцать предметов называли во многих европейских языках словами, схожими с русским словом «дюжина»: duodezim на латыни, douzaine на французском, dozzina на итальянском, dozen на английском. Римляне пользовались двенадцатеричными дробями, \frac1{12} они называли унцией.

В Европе счет дюжинами долгое время, вплоть до XVIII века, сохранялся наравне с десятеричной системой. Дюжина дюжин составляла гросс (от немецкого слова «большой»), дюжина гроссов — массу. Признаки влияния числа 12 заметны в англо-американской системе линейных мер, в которой 1 фут равен 12 дюймам, 1 дюйм — 12 линиям, 1 линия — 6 точкам.

Шестидесятеричная

Первой позиционной системой счисления считается шестидесятеричная система в Древнем Вавилоне. Ее основание до сих пор применяют для измерения времени. Система счисления времени — смешанная, но для перевода минут в секунды или часы потребуется именно шестидесятеричная система.

Для измерения углов и записи координат (широты, долготы) тоже используют эту систему, так как изначально астрономические координаты записывали в шестидесятеричных дробях. По аналогии с часом градус делят на шестьдесят минут, минуту — на шестьдесят секунд.

Двадцатеричная

Двадцатеричную систему называют вигезимальной. Эта система, как и десятеричная, связана с количеством пальцев, поэтому многие народы изобрели ее независимо друг от друга. Основание 20 сохранилось в лингвистической структуре их языков, именно на нем основана система счета в разговорной речи. Например, во французском языке «восемьдесят» состоит из слов «четыре» и «двадцать».

Таблицы истинности

При помощи тех же нулей и единиц создаются таблицы истинности логических выражений, в которых описаны всевозможные варианты.

Основные логические операции

Например, конъюнкция является одной из логических операций. Она является истиной только в том случае, если два высказывания имеют истинные значения.

Логические переменные таблицы истинности обозначают p и q, а их значения выражают при помощи 0 и 1, где 0 – ложь, 1 – истина:

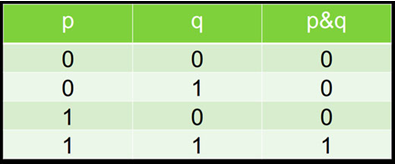
Фрагмент таблицы истинности для конъюнкции.

Так выражаются условия для всех логических операций.

Применяются таблицы истинности еще с начала 20 века в алгебре, логике, программировании.

Римская система счисления

Описание

Римская система счисления относится к непозиционным. Она известна всему миру и широко применяется до сих пор. Это связано не с какими-то особыми достоинствами, а скорее с политическим и культурным влиянием Древнего Рима на европейскую цивилизацию.
Сейчас римская система используется в русском языке для обозначения:

• веков;
• месяцев (при этом день и год пишут арабскими цифрами);
• валентности химических элементов;
• порядковых номеров монархов;
• номеров корпусов Вооруженных сил;
• групп крови;
• номеров томов многотомных книг, иногда номеров глав или параграфов;
• важных событий (XX съезд КПСС, II Мировая война, ХХ Олимпиада).

В других странах свои особенности употребления римских цифр: в Европе ими часто записывают номер года, в Латвии — день недели.
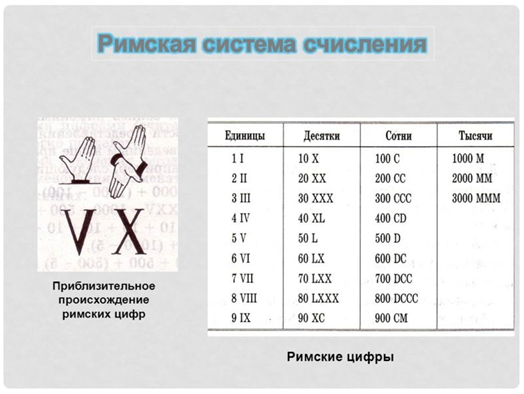
Считается, что в основу римских цифр легли жесты:

• I — единица, один палец;
• V — пять, ладонь;
• Х — десять, две скрещенные ладони.

100 и 1000 обозначаются буквами C и М — первыми буквами соответствующих латинских слов.

Основные характеристики

Для записи чисел используют семь букв латинского алфавита:

• I — 1;
• V — 5;
• X — 10;
• L — 50;
• C — 100;
• D — 500;
• M — 1000.

Сначала записываются тысячи, потом сотни, потом десятки и единицы. Ноль в системе отсутствует, но раньше вместо него использовали букву N. От позиционных систем римская отличается использованием принципов сложения и вычитания. Когда большая цифра стоит перед меньшей, они складываются. Когда меньшая стоит перед большей — вычитаются.

Позиционные и непозиционные системы счисления

Системой счисления называется совокупность приемов и правил представления чисел с помощью цифровых знаков.

Непозиционной называется такая система счисления, в которой значение любой цифры не зависит от положения (позиции) в ряду цифр, изображающих это число.

Например, в числе ХХХ, записанном в римской системе счисления, каждый разряд означает 10 единиц.

Задача 1. Записать числа в римской нумерации: а) 193; б) 564; в) 2708.

Позиционной называется такая система счисления, в которой значение любой цифры зависит от ее положения (позиции) в ряду цифр, изображающих это число.

Например, цифра 3 в числе 723, записанном в десятичной системе счисления, означает три единицы, а в числе 325 – три сотни. К позиционным СС можно отнести шестидесятиричную вавилонскую и десятичную системы счисления.

Под основанием системы счисления понимается определенное постоянное для данной системы счисления отношение единиц соседних разрядов.

Основанием системы счисления может быть любое натуральное число большее 1.

Система счисления с основанием равным 1 называется унарной.

Для записи чисел в позиционной системе счисления используются цифры, количество которых соответствует основанию системы.

Десятичная система счисления, запись чисел в ней

В практике установилась десятичная система счисления. Как известно, в десятичной СС для записи чисел используются 10 знаков (цифр): 1,2,3,4,5,6,7,8,9,0. Из них образуются конечные последовательности, которые являются краткими записями чисел. Например, последовательность 3745 является краткой записью числа

Определение 4.Десятичной записью натурального числа xназывается его представление в виде:

где коэффициенты a_n, a_n-1, …, a₁, a принимают значения 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и

Сумму

Так как понятие числа и его записи нетождественны, то существование и единственность десятичной записи натуральной записи надо доказывать.

Теорема 1. Любое натуральное число х можно представить в виде:

где коэффициенты a_n, a_n-1, …, a₁, a принимают значения 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

и такая запись единственная.

Десятичная запись числа позволяет просто решать вопрос о том, какое из них меньше.

Теорема 2. Пусть х и у – натуральные числа, запись которых дана в десятичной системе счисления:

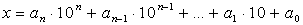
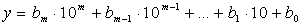
Тогда число х меньше числа у, если выполнено одно из условий:

Три первых разряда в записи числа соединяют одну группу и называют первым классом, или классом единиц. В первый класс входят единицы, десятки и сотни.

Четвертый, пятый и шестой разряды в записи числа образуют второй класс – класс тысяч. Затем следует третий класс – класс миллионов, состоящий тоже из трех разрядов: седьмого, восьмого и девятого, т.е. из единиц миллионов, десятков миллионов и сотен миллионов.

Последующие три разряда также образуют новый класс и т.д. выделение классов единиц, тысяч, миллионов и т.д. создает удобства для записи и прочтения чисел.

В десятичной СС всем числам можно дать название (имя). это достигается следующим образом: имеются названия первых 10 чисел, затем из них в соответствии с определением десятичной записи и путем прибавления еще немногих слов образуются названия последующих чисел. Так числа второго десятка, представляемые в виде

Может быть естественнее было бы говорить «два и десять», но наши предки предпочли говорить «два на десять», что и сохранилось в речи.

Таким образом, чтобы назвать все натуральные числа в пределах миллиарда, потребовалось только 16 различных слов: один, два, три, четыре, пять, шесть, семь, восемь, девять, десять, сорок, девяносто, сто, тысяча, миллион, миллиард. Остальные названия чисел (в пределах миллиарда) образуются из основных.

Что представляет собой позиционная система счисления?

Рассматриваемая система счисления характеризуется тем, что цифры в ней в зависимости от своей позиции относительно начала числа (при его прочтении слева направо) будут иметь разную силу. Чем правее расположена цифра — тем она слабее. Например, в числе 143 самая сильная цифра — 1, поскольку обозначает сотню, далее по силе — 4, поскольку она обозначает десяток, третья по силе цифра — 3, так как она соответствует единичному числу.

Систем счисления, считающихся позиционными, в мире используется довольно много. В числе самых распространенных — двоичная (применяется в программировании), десятичная (более всего распространена в повседневной жизни), восьмеричная и шестнадцатеричная (в основном они применяются в инженерном деле).

Что представляет собой непозиционная система счисления?

Соответствующая система счисления характеризуется тем, что цифры в ней не всегда делятся по силе в зависимости от позиции относительно начала числа. Разность в их силе, в принципе, возможна, но не всегда является правилом.

Например, римское число XX (двадцать) состоит из двух одинаковых по силе цифр X, каждая из которых обозначает десять. В свою очередь, в числе XV (пятнадцать) первая цифра сильнее, поскольку соответствует десятичному основанию, а вторая — единичному числу пять.

Кроме того, в непозиционной системе счисления, в которой используются римские цифры, число, расположенное левее, может быть более слабым. Например, римская цифра IV, то есть 4, состоит из более слабой, расположенной левее I(единицы) и более сильной, расположенной правее V (пять). Цифра 4 образуется, таким образом, посредством вычитания более слабой цифры из более сильной.