Основные отличия между медианой и биссектрисой: почему их путают

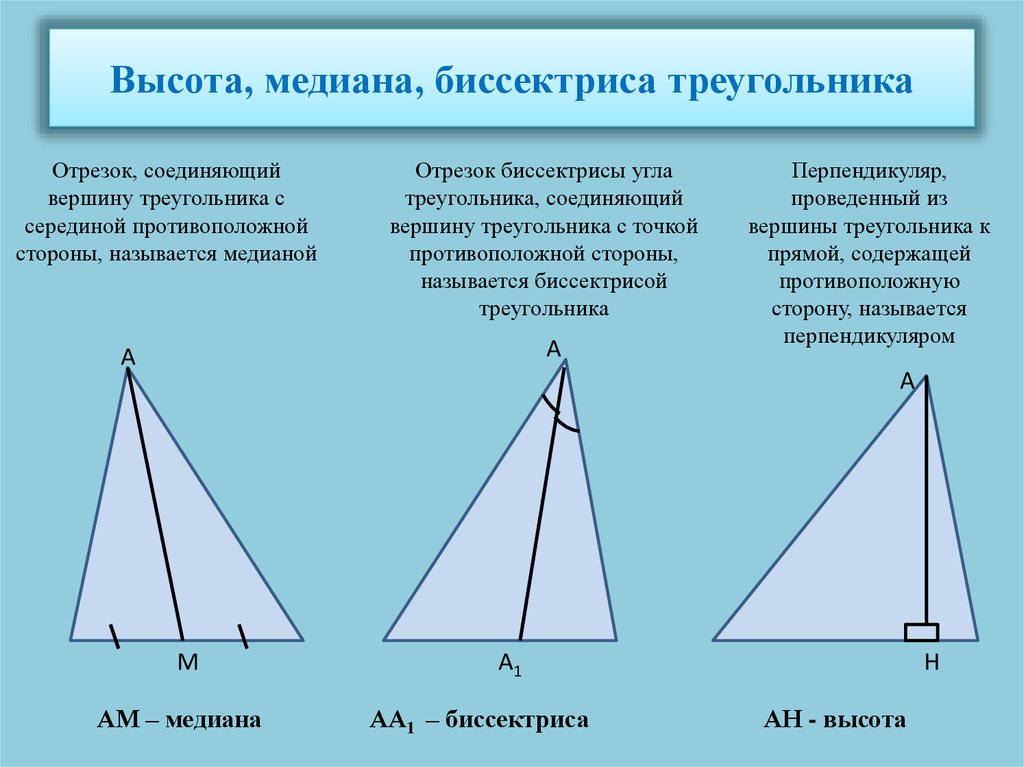
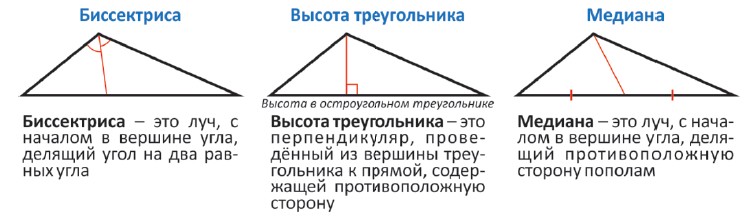
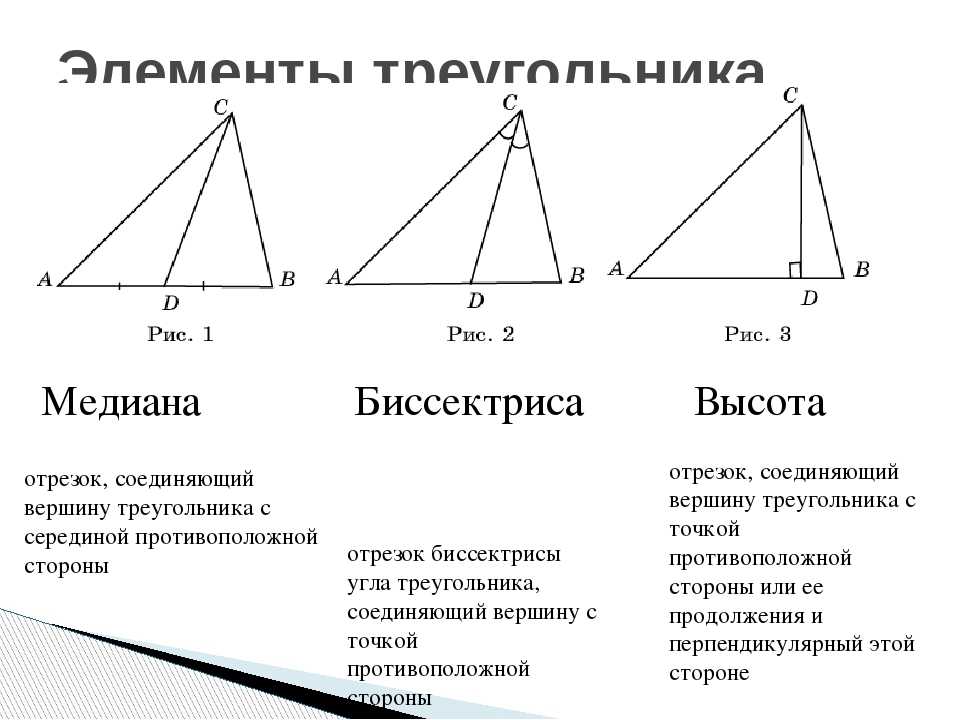
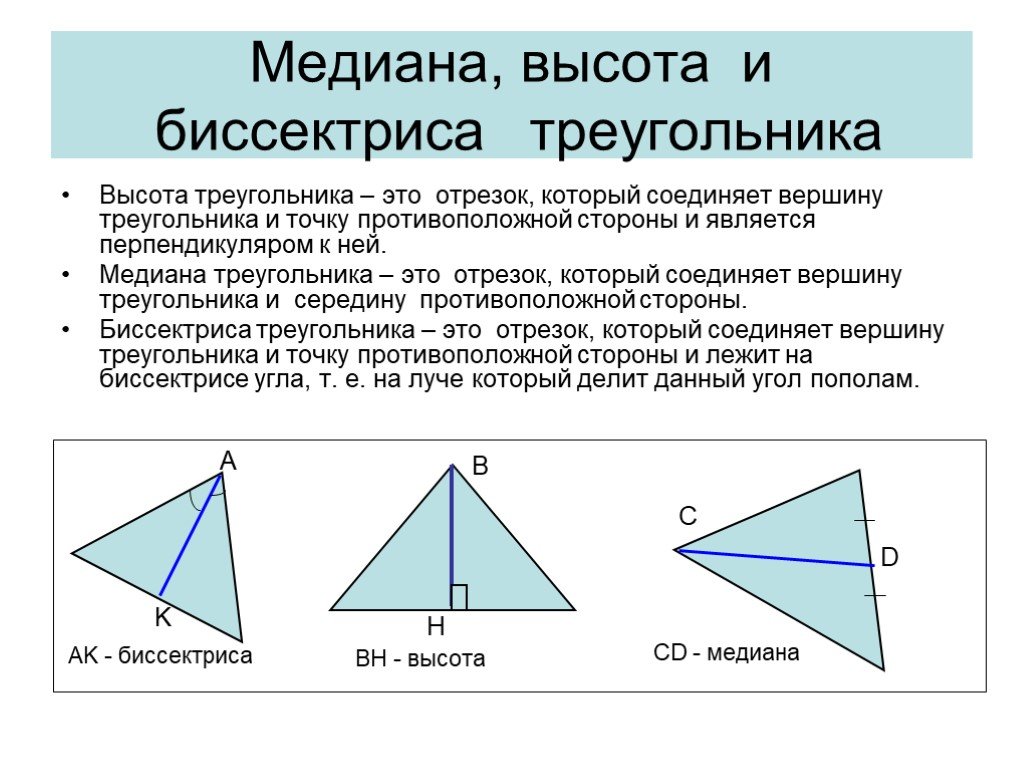
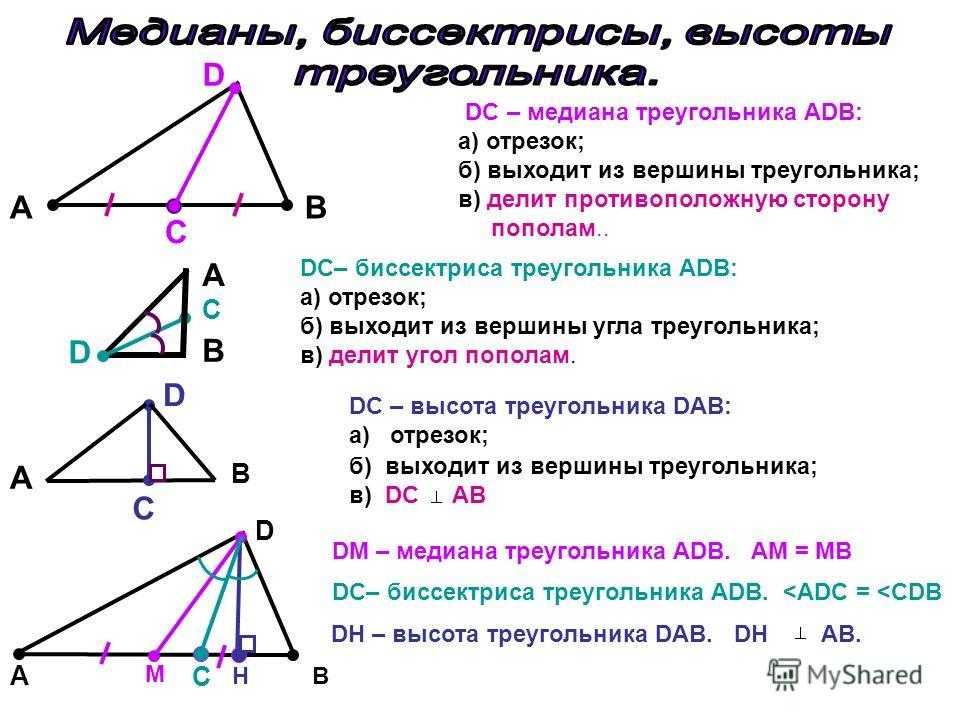
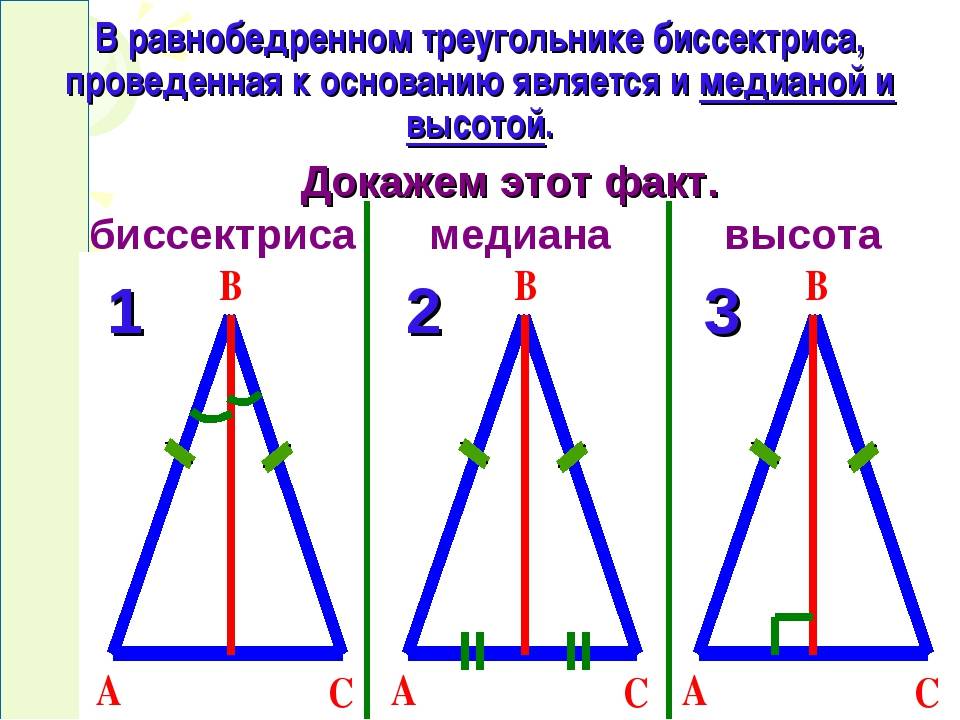
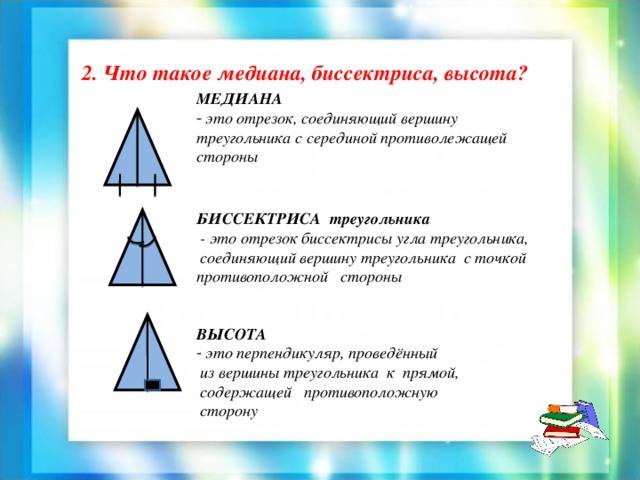
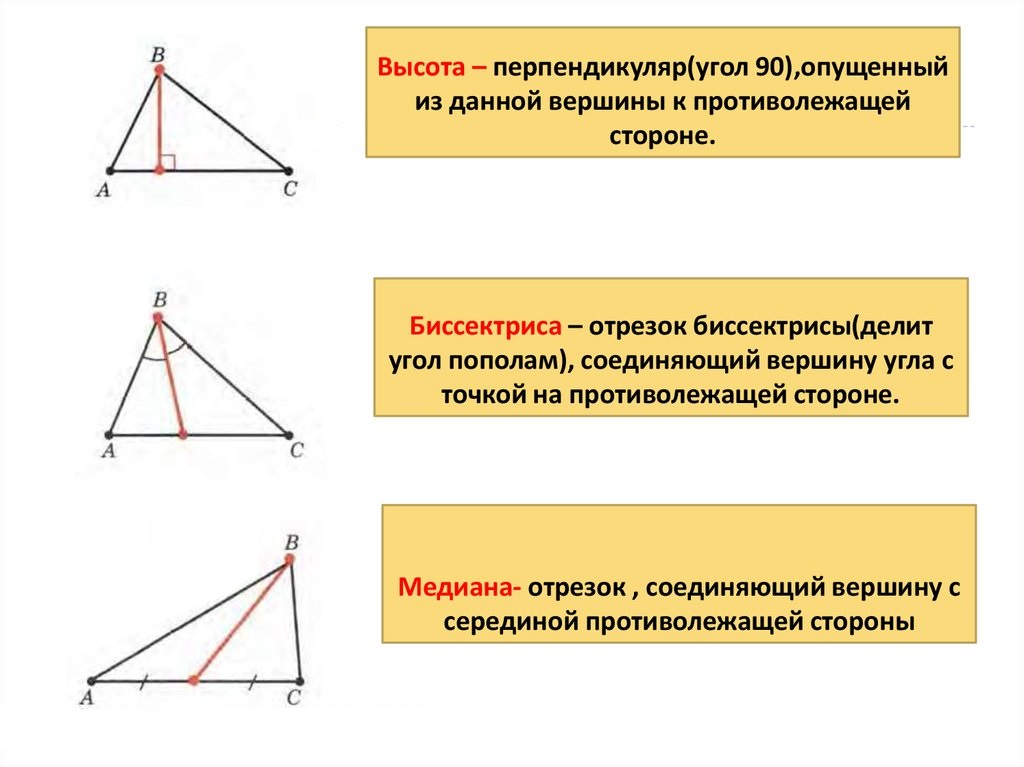
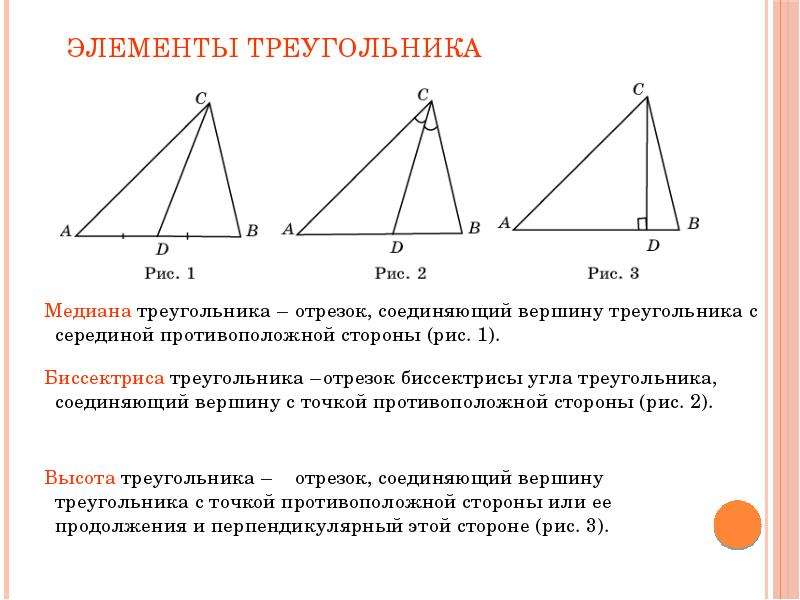
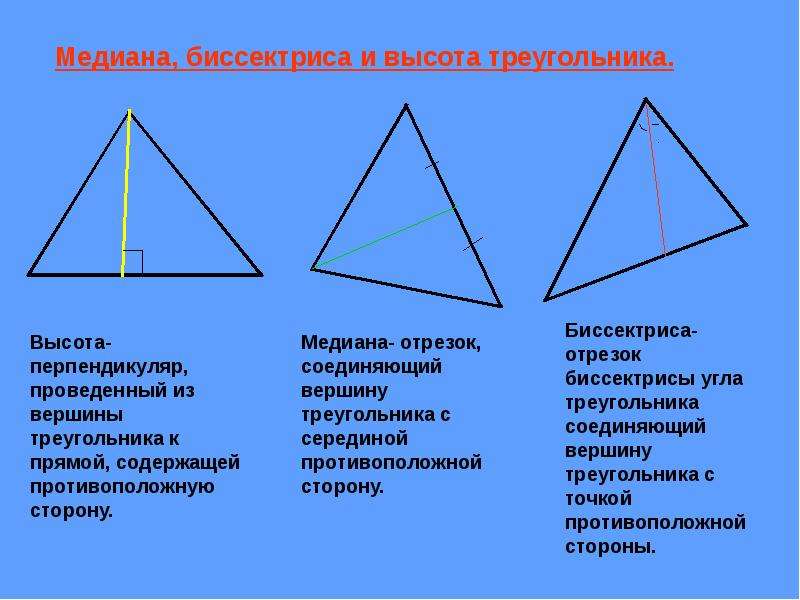
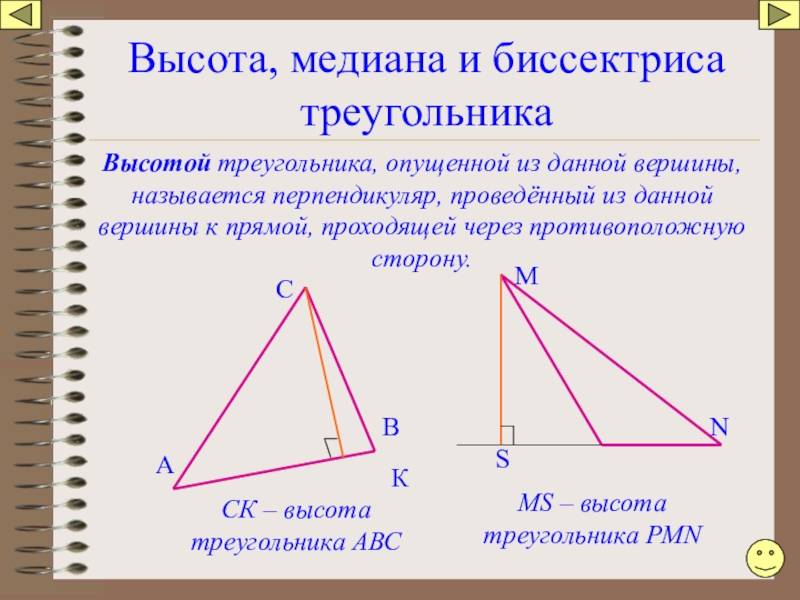
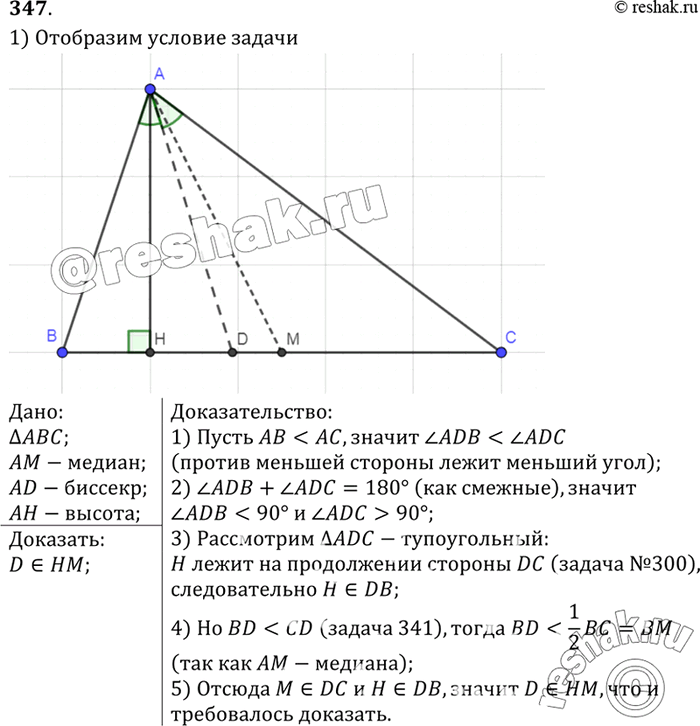
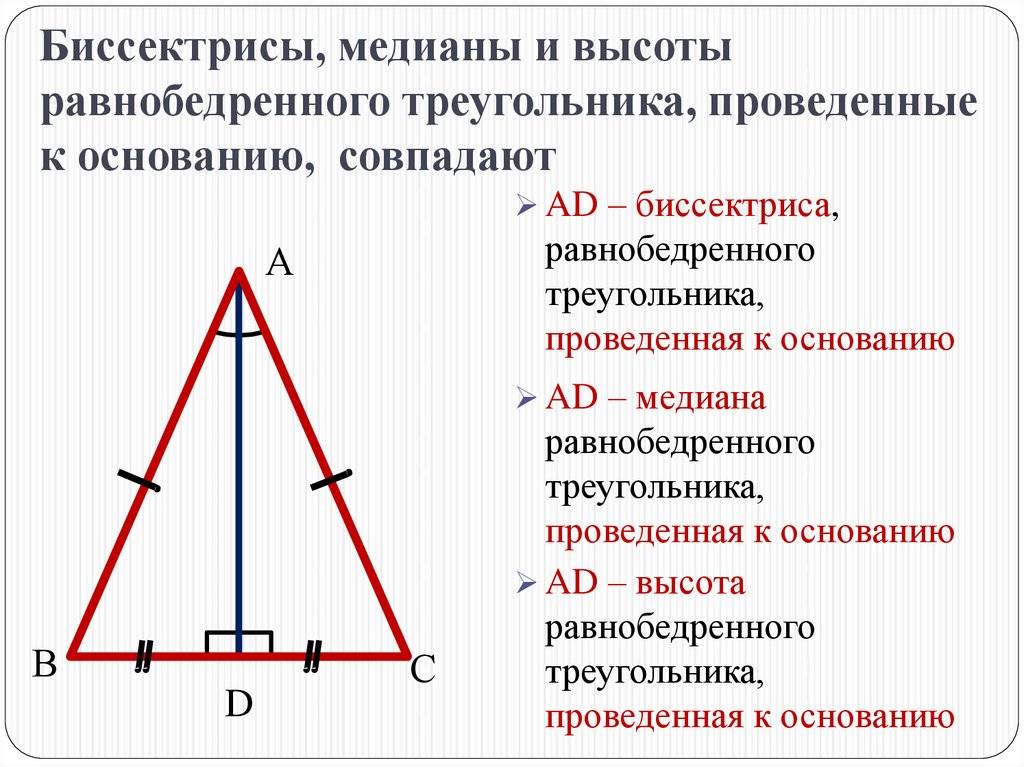
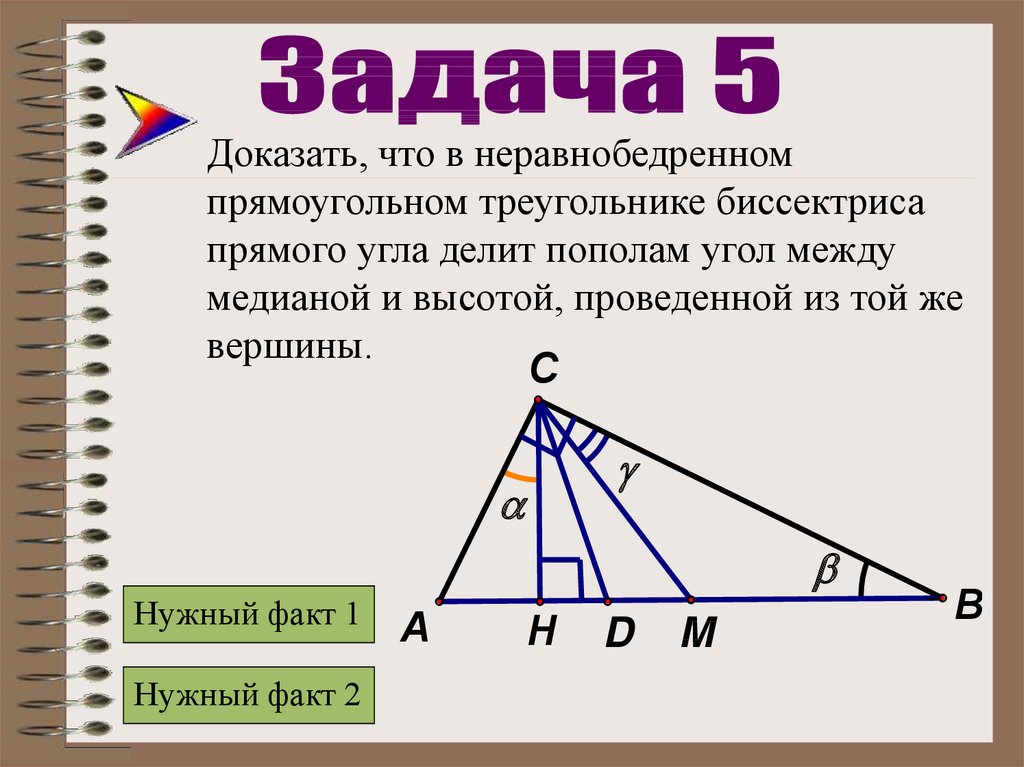
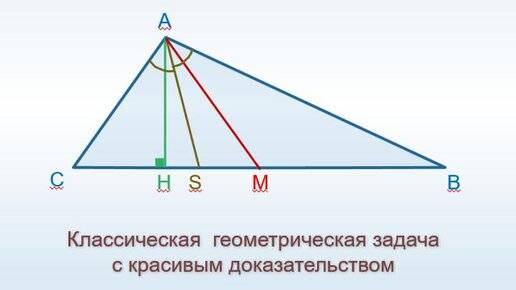
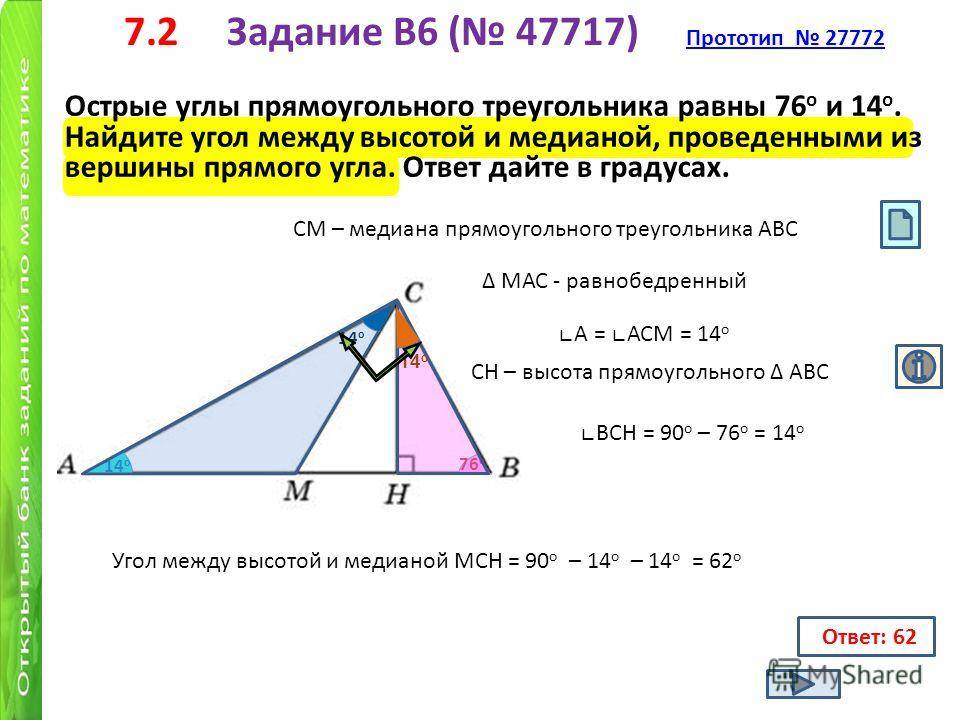
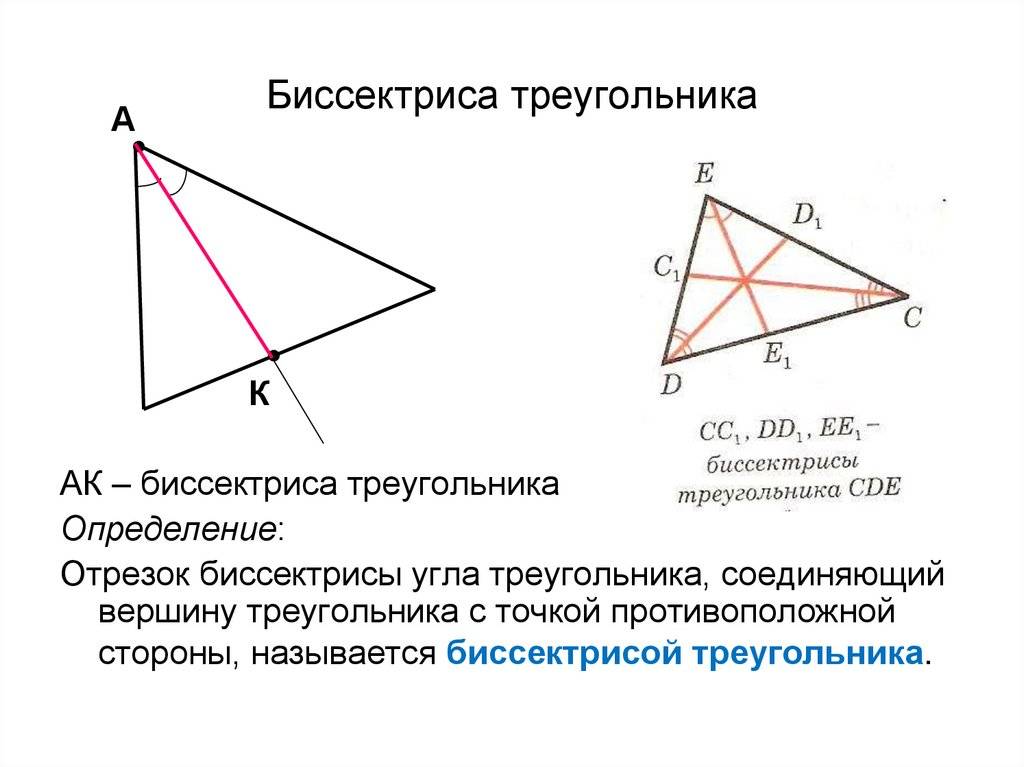
Свойства биссектрисы треугольника

1. Каждая точка этой линии равноудалена от сторон угла. Часто эту характеристику выбирают в качестве определения, поскольку верно и обратное утверждение для любого произвольного треугольника. Это позволяет находить и радиус вписанной окружности.

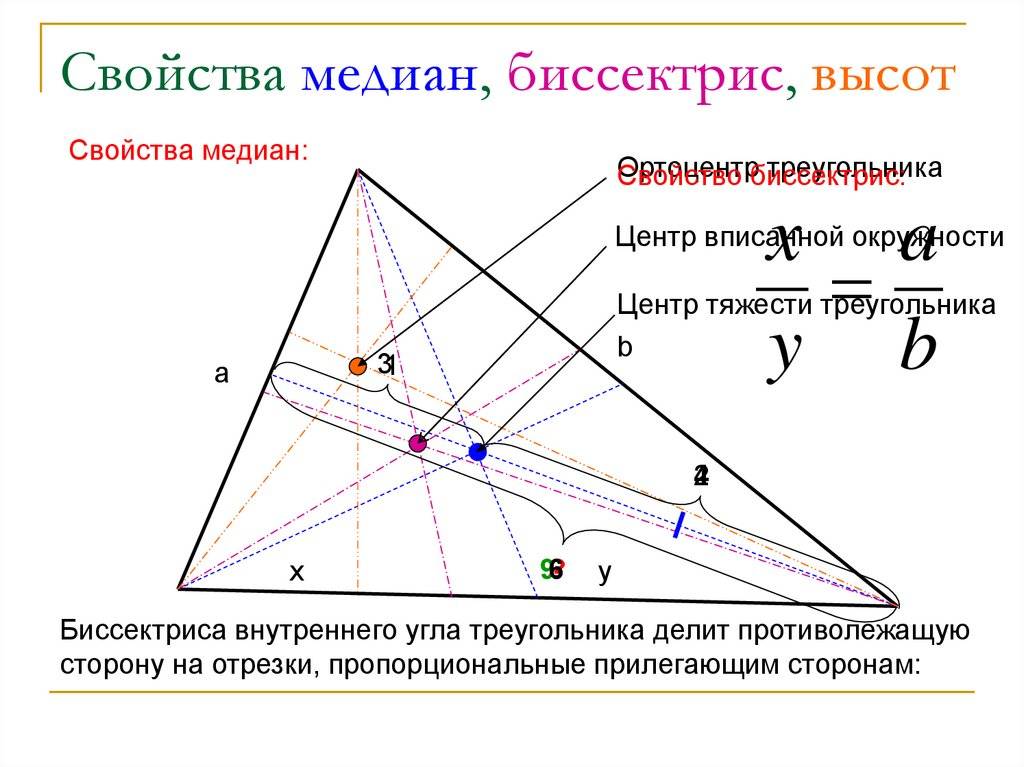
2. Все внутренние отрезки, делящие углы пополам, пересекаются в одной точке, которая является центром окружности, вписанной в фигуру, т. е. точка пересечения находится на равных расстояниях от сторон.

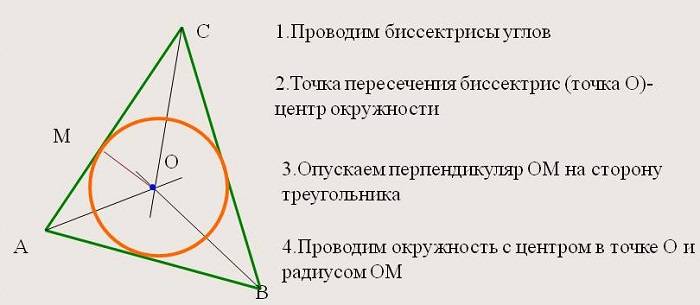
Данное свойство позволяет решать целый класс разнообразных задач, выводить формулы для радиусов вписанных окружностей правильных многоугольников.

Благодаря этому утверждению, легко доказывается следующее правило:

Площадь описанного многоугольника равна:

S = p∗r

где p – полупериметр, а r – радиус вписанной окружности.

Это позволяет находить решение не только планиметрических, но и стереометрических задач.

Важную роль играют внешние биссектрисы треугольника. Вместе с внутренними они образуют прямые углы;

3. Сумма величин двух прилежащих сторон, делённая на длину противолежащей стороны, задаёт отношение частей биссектрисы (считая от вершины), полученных точкой пересечения всех трёх соответствующих линий.

Некоторые виды геометрических фигур, в силу своих особенностей, порождают особые примечательные характеристики;

4. В равнобедренном треугольнике биссектриса, проведённая к основанию, одновременно является медианой и высотой. Две другие – равны между собой.

В этом случае основание параллельно внешней биссектрисе.

Обратное положение также имеет место. Если прямая проведена параллельно основанию равнобедренного треугольника через некоторую вершину, то внешняя биссектриса при этой вершине является частью этой линии;

Для равностороннего многоугольника важной характеристикой считается равенство всех биссектрис;. 6

У правильного треугольника все внешние биссектрисы параллельны сторонам;

6. У правильного треугольника все внешние биссектрисы параллельны сторонам;

7. Выделяют несколько особенностей, среди которых есть следующая теорема:

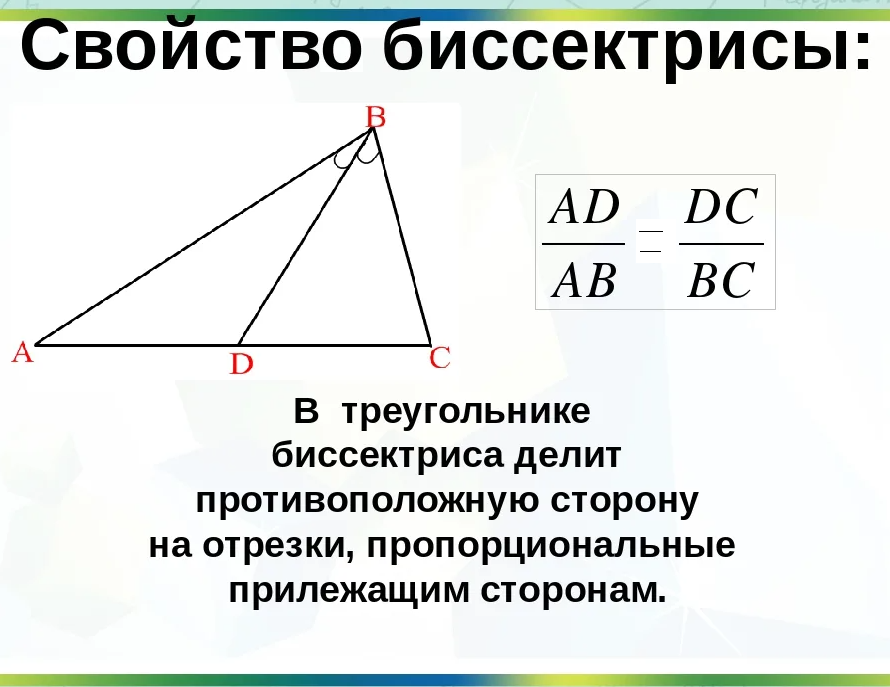
«Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам».

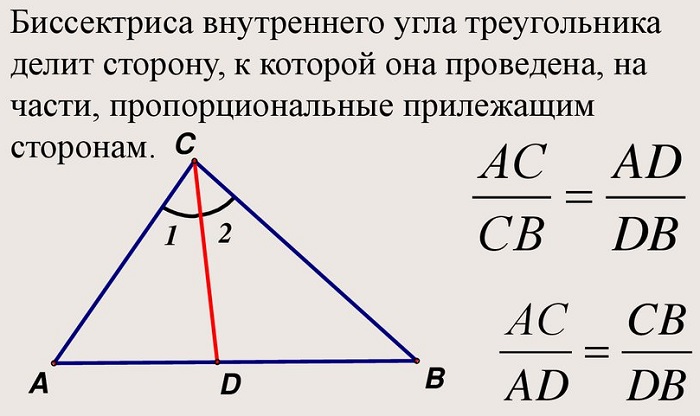
Обратное утверждение («Прямая делит сторону на отрезки, пропорциональные двум другим сторонам») выражает признаки того, что рассматриваемая линия является внутренней биссектрисой;

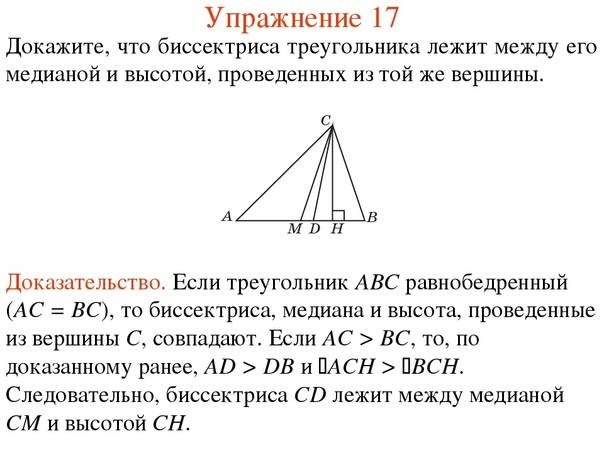
8. Разносторонний треугольник позволяет определить взаимное расположение его высоты, медианы и биссектрисы, проведённых из одной точки. В частности, медиана и высота располагаются по разные стороны от третьей линии.

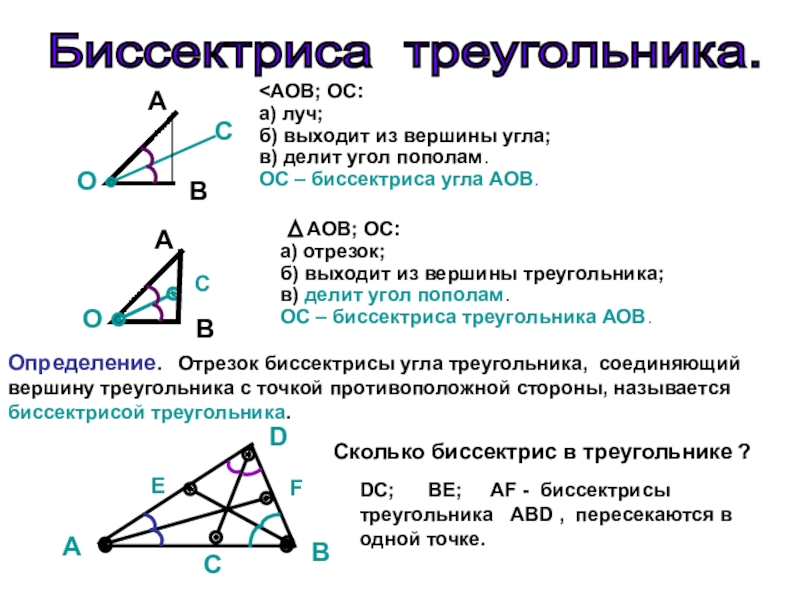
Биссектриса: понятие и особенности

Основные особенности биссектрисы:

1. Биссектриса является внутренним перпендикуляром к стороне угла, который она делит.

2. Биссектриса равноудалена от сторон угла.

3. Если биссектрисы двух углов пересекаются, то точка пересечения лежит на вписанной окружности, вписанной в данный угол.

Применение биссектрисы:

1. Биссектриса используется при построении треугольников и многоугольников.

2. Биссектриса является важным элементом для проведения перпендикуляра к линии.

3. Биссектриса может использоваться для нахождения середины отрезка, деления отрезка на определенные части и других геометрических задач.

Биссектриса является одним из важных элементов геометрии, который широко применяется в различных областях, таких как строительство, дизайн, картография и другие.

Биссектриса и ее свойства

Свойства биссектрисы в треугольнике:

Свойство	Описание
1.	Биссектриса делит противоположную сторону треугольника на отрезки, пропорциональные прилегающим сторонам.
2.	Биссектриса перпендикулярна медиане, проведенной из точки пересечения биссектрисы со стороной треугольника.
3.	Биссектриса равноудалена от двух сторон треугольника.
4.	Сумма длин двух сегментов, на которые биссектриса делит противоположную сторону, равна длине биссектрисы.

Знание свойств биссектрисы позволяет решать разнообразные задачи по нахождению размеров и отношений сторон и углов в треугольнике. Биссектриса является важным элементом треугольника и находит свое применение в геометрических вычислениях и построениях.

Теорема о длине высоты треугольника

Для нахождения длины высоты треугольника можно расписать его площадь двумя способами. Во-первых, используя формулу Герона, во-вторых, как половину произведения высоты на основание, к которому проведена данная высота.

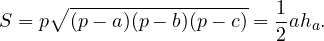
здесь — полупериметр треугольника.

Из сравнения данных формул находим:

Отметим, что это лишь один из способов нахождения длины высоты треугольника по его сторонам, который удобен далеко не всегда. Существует огромное множество альтернативных способов, с которыми читатель может ознакомиться в предыдущих уроках.

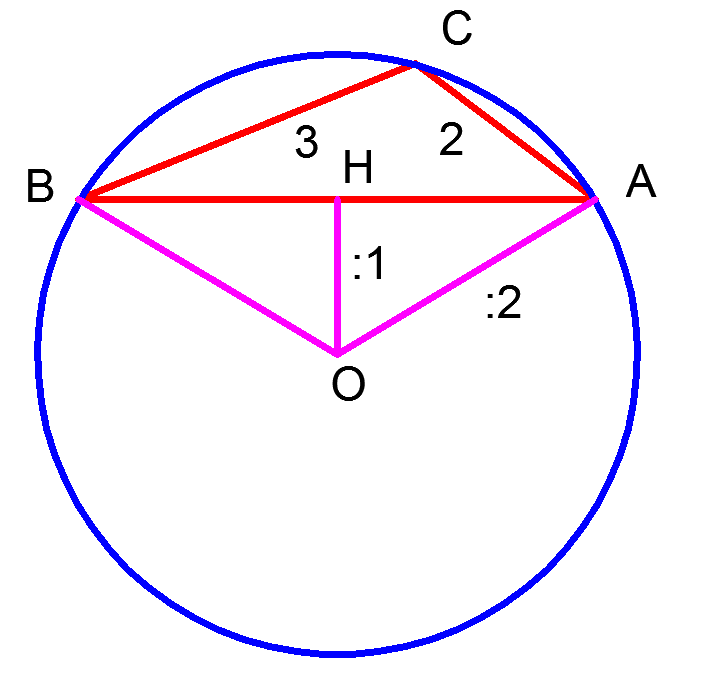
Пример 1. Известно, что расстояние от центра описанной окружности до стороны AB треугольника ABC равняется половине радиуса этой окружности. Найдите высоту треугольника ABC, опущенную на сторону AB, если она (высота) меньше а две другие стороны равны 2 и 3.

Решение. Треугольник BOA на рисунке является равнобедренным, поэтому ∠ OAH = ∠ OBH = 30° (катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы). Тогда ∠ BOA и соответствующая дуга окружности, на которую он опирается, равны по 120°. Тогда дуга, на которую опирается ∠ BCA, равна 240°, а значит сам угол ∠ BCA = 120°.

Площадь треугольника ABC находим по формуле: Длину стороны AB находим по теореме косинусов для треугольника ABC, она равна . С другой стороны, площадь треугольника есть половина произведения высоты на основание, к которому данная высота проведена. Отсюда выражаем требуемую длину высоты что меньше Случай с остроугольным треугольником ABC не подходит. Проверьте самостоятельно.

Задача для самостоятельного решения №1. В остроугольном треугольнике ABC BC = a, AC = b, ∠ ACB равен α. Найти высоту CD и ∠ ABC.

Показать ответ
Ответ:

Высота треугольника

Пусть нам дан треугольник $\bigtriangleup{ABC},$ где из вершины $C$ к противолежащей стороне $AB$ опущен отрезок $CD$, образующий при этом перпендикуляр к стороне $AB$. Тогда отрезок $CD$ будет являться высотой треугольника $\bigtriangleup{ABC}$. Аналогичный перпендикуляр можно опустить как из вершины $A$, так и из вершины $B$.

Получается, что:

В остроугольном треугольнике — где углы имеют значение $<90^{\circ}$ — чертеж высот не вызывает сложности: они всегда будут пересекаться внутри треугольника. Однако если треугольник тупоугольный — один из углов имеет значение $>90^{\circ},$ — провести высоту будет уже не так интуитивно просто.

Осмотрите треугольник $\bigtriangleup{PMK}$ выше, с тупым углом $\angle{M}$.

Нам необходимо провести высоту из вершины $K$ к стороне $PM$. Подумайте, как будет располагаться отрезок, выполните чертеж и сравните свои предположения со скрытым чертежом.

Пересечение высот: как найти высоту треугольника

Выходит, что в остроугольном треугольнике высоты пересекаются в точке, расположенной строго внутри треугольника — никаких дополнительных построений не требуется.

Высоты в тупоугольном треугольнике пересекаются в точке, расположенной вне треугольника, — чтобы найти высоту треугольника, необходимо достраивать продолжение сторон

Так, в случае с нашим тупоугольным треугольником, высоты пересекаются в точке $O$ — внимание на чертеж выше

{"questions":[{"content":"`image-1` Помимо остроугольного и тупоугольного треугольника, существует треугольник прямоугольный — частный случай, когда один из углов прямой, то есть равняется $90^{\\circ}$. Что это за треугольник и какими свойствами он обладает, подробнее мы разберем далее в курсе геометрии. Пока что давайте просто поразмышляем: а где же будут <b>пересекаться высоты</b> в прямоугольном треугольнике?  `choice-11`","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/02/test-right.svg","width":"500"},"choice-11":{"type":"choice","options":,"explanations":["","","","Это очень логично! <br /><br />В треугольнике $\\bigtriangleup{ABC}$ сторона $AB$ является высотой к стороне $BC$, и наоборот, ведь $\\angle{B}$ — прямой. Высота к стороне $AC$ будет выходить из вершины $B$. Так что точка пересечения высот в прямоугольном треугольнике, получается, располагается в точке $B$ — в вершине прямого угла."],"answer":}}}]}

Применение медианы и биссектрисы в разных областях

Медиана — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Применение медианы в разных областях достаточно широко. Например, в математике медиана используется для нахождения медианного значения данных, что позволяет получить более репрезентативную информацию о выборке. В географии медианы применяются для определения точки равновесия распределения населения. Также медиану можно использовать в медицине для определения наиболее характерных показателей здоровья в группе пациентов.

Биссектриса — это линия, делящая угол на две равные части. Биссектриса также имеет различные применения в разных областях. В архитектуре она используется для создания симметричных и гармоничных конструкций. В физике биссектриса может быть использована для нахождения угла падения и отражения светового луча. В образовании биссектриса помогает учащимся лучше понять свойства углов и треугольников.

Таким образом, медиана и биссектриса являются важными концепциями геометрии, которые находят применение в разных областях. Они отличаются друг от друга по своему назначению и способам использования, но играют важную роль в решении различных задач.

География

Медиана — это линия, проведенная из вершины треугольника к середине противоположной стороны. Медиана делит сторону треугольника на две равные части и проходит через центр масс треугольника. Медианы используются в географии для определения центра масс географических объектов, исследования плотности населения и других параметров.

Биссектриса — это линия, которая делит угол на две равные части. В географии биссектрисы используются, например, для определения середины границы между двумя государствами или провинциями.

Отличие медианы от биссектрисы заключается в том, что медиана делит сторону треугольника, а биссектриса делит угол. Применение медианы и биссектрисы зависит от конкретной задачи в географии, но оба понятия помогают ученым и исследователям анализировать и описывать различные аспекты нашей планеты и ее географических объектов.

Архитектура

Различие между медианой и биссектрисами заключается в их направлении и функциях. Медиана направлена от вершины к середине противоположной стороны и используется для распределения и равномерного расположения элементов. Биссектрисы направлены от угла треугольника к противоположной стороне и служат для создания симметричных и сбалансированных форм.

В архитектуре медианы и биссектрисы применяются для создания гармоничного и пропорционального дизайна. Они помогают уравновесить элементы по горизонтали и вертикали, создать симметрию и достичь эстетического баланса. Эти линии помогают архитекторам создавать привлекательные и удобные пространства, которые приятно воспринимать как визуально, так и функционально.

Медицина

Медиана — это статистический показатель, который используется для нахождения среднего значения в наборе данных. В медицине медиана может быть использована для определения среднего значения какой-либо характеристики у большой группы пациентов.

Однако, медицина отличается от медианы не только в использовании статистических показателей. Медицина — это комплекс научных, профессиональных и практических знаний, которые направлены на сохранение и восстановление здоровья людей.

Основными целями медицины являются предотвращение, диагностика и лечение заболеваний, а также поддержание и улучшение общего физического и психического состояния человека.

Медицина включает в себя различные специальности, такие как терапия, педиатрия, хирургия, неврология, гинекология и другие. Каждая специальность имеет свои особенности и применяет свои методы для диагностики и лечения пациентов.

Все врачи и медицинский персонал, работающие в области медицины, должны иметь высокую квалификацию и навыки, чтобы предоставлять качественную медицинскую помощь своим пациентам.

Вместе с тем, медицина постоянно развивается и совершенствуется. Врачи и ученые работают над разработкой новых методов диагностики и лечения, а также над открытием новых лекарственных препаратов.

Отличие медицины от медианы заключается не только в применении определенных показателей и методов. Медицина — это сложная и важная область, которая направлена на сохранение и повышение здоровья человека.

Медицина играет огромную роль в нашей жизни и оказывает влияние на все сферы общества. Благодаря медицине люди имеют возможность лечиться и продолжать вести полноценный и здоровый образ жизни.

Биссектриса

Биссектрисой называют луч, исходящий из любого угла к противоположной стороне. В отличие от медианы, он делит угол на две равные половины, а не сторону, поэтому точки пересечения обеих линий с общей гранью могут быть разными.

Начертить биссектрису не сложно, достаточно выполнить три простые действия:

Провести луч из любой точки (А, В, С) фигуры так, чтобы он разделил угол пополам
Зафиксировать точку на противолежащей стороне фигуры
Соединить общей линией отрезок между точками входа и выхода

В качестве примера рассмотрим рисунок ниже:

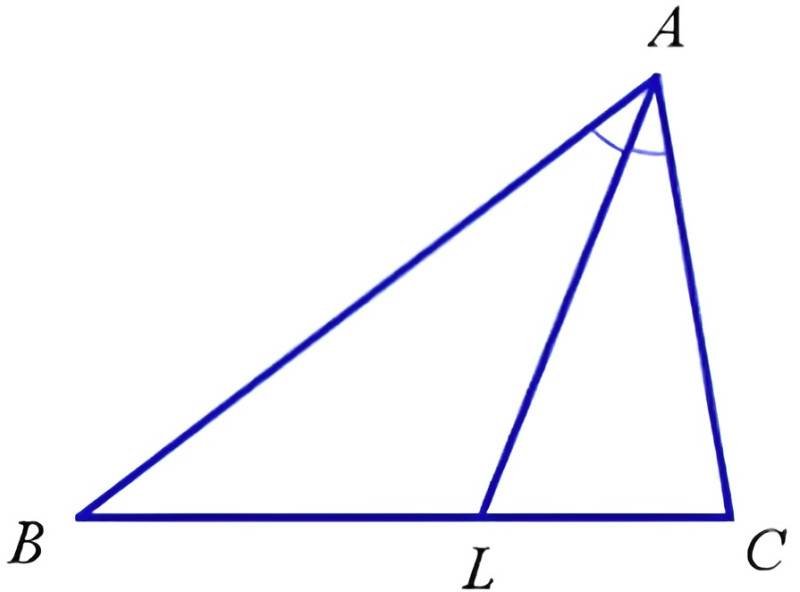
В нашем случае у треугольника АВС из вершины А проходит линия, разделяющая угол пополам. Место пересечения с гранью фигуры обозначено буквой L, соответственно, линия AL будет биссектрисой.

Равнобедренный треугольник и медиана

Равнобедренным треугольником называют фигуру, у которой есть две одинаковые по размеру стороны. Такие грани называются боковыми, а нижняя — это основание. Как выглядит такая фигура, можно увидеть на рисунке ниже:

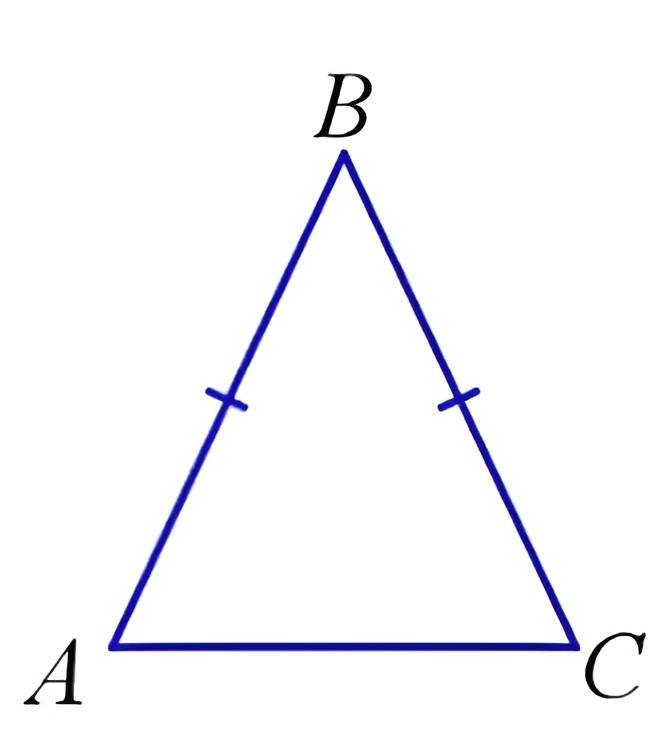
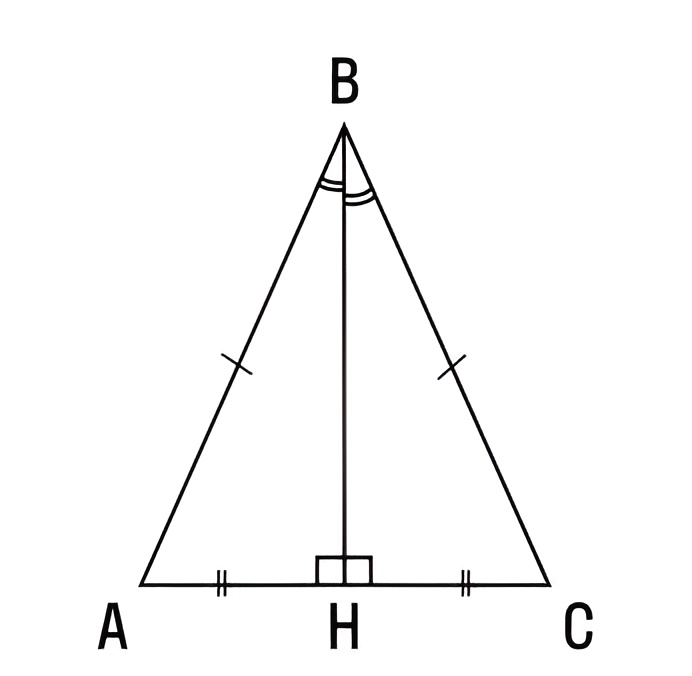
Как это доказать, рассмотрим на простом примере. Первое, что нам понадобится, — это доказательство того, что фигуры АВН и СВН симметричны.

Для этого представим, что ВН будет биссектрисой. Учитывая, что речь идет о равнобедренном треугольнике, грани АВ и ВС равны по своей длине.

Угол А равен углу С, как и оба угла при общей вершине В (свойство биссектрисы). При этом ВН — это общая грань, значит, треугольники АВН и СВН одинаковы.

Отрезки АН и СН также равны, поэтому ВН — это медиана. При одинаковых значениях углов у точек А и С сумма двух углов по обе стороны от точки Н будет равна 180 градусов. Значит, каждый угол равен 90 градусов, что доказывает, что ВН — это высота.

Итог: любой луч, который можно провести из верхней точки треугольника перпендикулярно основанию, будет совмещать в себе высоту, медиану и биссектрису.

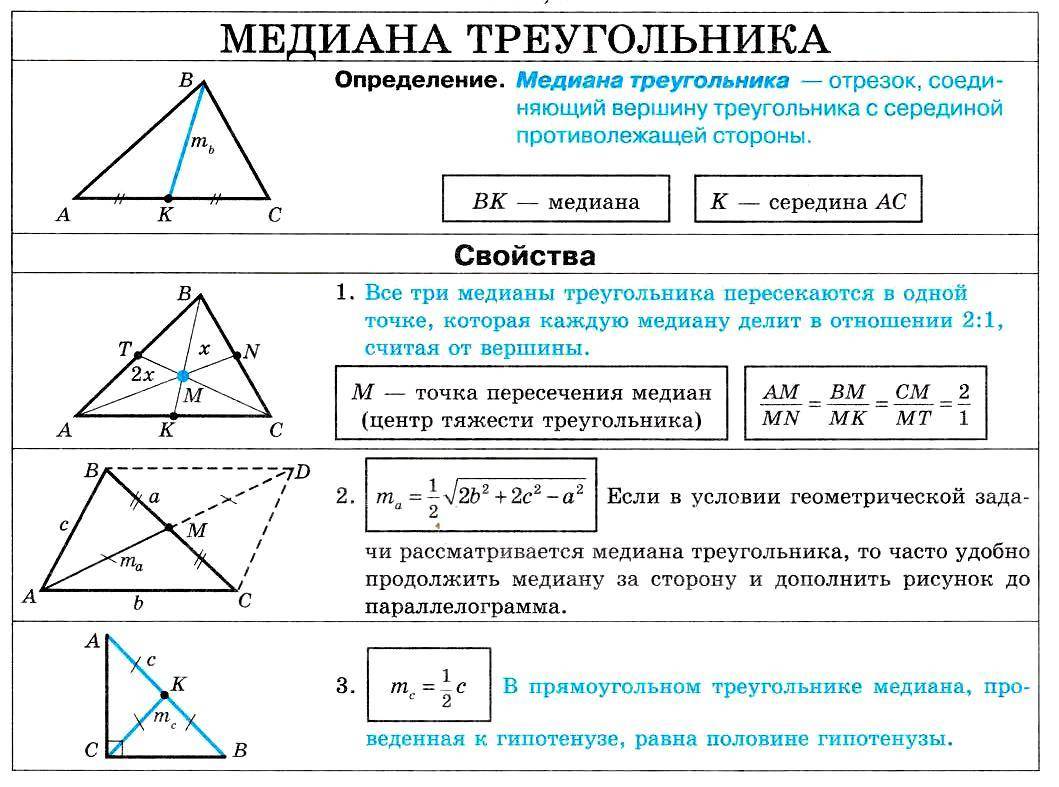
Теорема о длине медианы треугольника

Медиана треугольника определяется через три его стороны по формуле:

где a, b, c — стороны треугольника, m_a — медиана, проведенная к a. С доказательством этого утверждения интересующийся читатель может ознакомиться в видеоуроке.

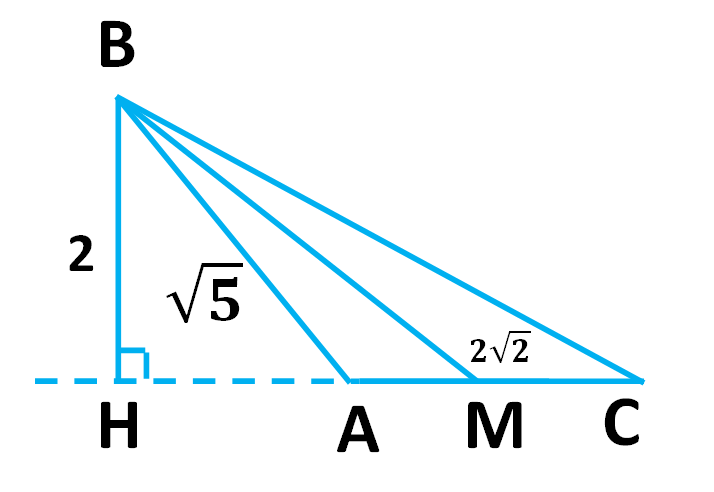
Пример 2. В треугольнике ABC со стороной AB = из вершины B к стороне AC проведены медиана BM = и высота BH = 2. Найдите сторону BC, если известно, что ∠ B + ∠ C < 90°.

Решение. Из анализа условия задачи делаем вывод, что ∠ A — тупой. Действительно, ведь сумма всех углов в треугольнике равна 180°. Находим по теореме Пифагора длину HA = 1. Далее по теореме Пифагора находим длину HM = 2. Следовательно, AM = HM — HA = 1. При этом AM = MC = 1 (т. к. BM — медиана). Итак, HC = HA + AM + MC = 3. Следовательно, по теореме Пифагора BC = . Прямой подстановкой убеждаемся в справедливости ранее полученной формулы для длины медианы треугольника.

Задача для самостоятельного решения №2. В треугольнике ABC медианы, проведенные к сторонам AC и BC, пересекаются под прямым углом. Известно, что AC = b, BC = a. Найдите длину стороны AB.

Показать ответ
Ответ:

Задачи

Все эти свойства несложно запомнить, они легко закрепляются на практике. Для большего понимания темы, решим несколько задач:

Рис. 2. Рисунок к задаче.

Для того, чтобы найти значение медианы, нам необходимо найти гипотенузу, так как медиана, проведенная к гипотенузе равна ее половине. Гипотенузу находим через теорему Пифагора: $$a^2+b^2=c^2$$

$$c=\sqrt{a^2+b^2}=\sqrt{9+16}=\sqrt{25}=5$$

Найдем значение медианы: $$m={c\over2}={5\over2}=2,5$$ – получившееся число и есть значение медианы.

Значения медиан в треугольнике не равны. Поэтому нужно обязательно представлять, какую именно величину необходимо найти.

Рис. 3. Рисунок к задаче.

Чтобы решить эту задачу нужно воспользоваться одной из трех формул для нахождения медианы по сторонам треугольника:

$$m^2 ={1\over2}*(b^2+c^2-a^2)$$

Как видно, главное здесь запомнить коэффициент при скобках и знаки у значения сторон. Знаки запомнить проще всего – вычитается всегда сторона, к которой опущена медиана. В нашем случае это a, но может быть любая другая.

Подставим значения в формулу и найдем величину медианы: $$m=\sqrt{{1\over2}*(b^2+c^2-a^2)}$$

$$m=\sqrt{{1\over2}*(49+81-64)}=\sqrt{33}$$ – оставим результат в виде корня.

Медианы, разбивают треугольник на шесть равновеликих. Значит, площади малых треугольников будут равны между собой. Достаточно найти площадь большего и поделить ее на 6.

Дана медиана, проведенная к основанию, в равнобедренном треугольнике она является биссектрисой и высотой. Значит, в треугольнике известны основание и высота. Можно найти площадь.

$$S={1\over2}*6*8=24$$

Площадь каждого из малых треугольников: $${24\over6}=4$$

Что мы узнали?

Мы узнали, что такое медиана. Определили свойства медианы, и нашли решение типовых задач. Поговорили о базовых ошибках и разобрались как просто и быстро запомнить формулу нахождения медианы через стороны треугольника.

/10
Вопрос 1 из 10
Медиана это
- Отрезок, соединяющий высоту с серединой противоположной стороны
- Сторона треугольника
- Перпендикуляр, опущенный из вершины на противоположную сторону
- То же ,что и серединный перпендикуляр

Окружность, вписанная в треугольник

Окружность, касающаяся всех трех сторон треугольника, называется вписанной окружностью. Только одна окружность может быть вписана в любой треугольник.

Центром пересечения биссектрис, как мы знаем, является инцентром. Инцентром еще называют центром вписанной окружности. Если от инцентрома до любого основания измерить расстояние по перпендикуляру, то мы получим радиус вписанной окружности.

Для того, чтобы вписать окружность в треугольник тебе, понадобится циркуль. Выставь циркуль в инцентром и установи радиус равный расстоянию до любого основанию по перпендикуляру. Круговым движением нарисуй окружность.

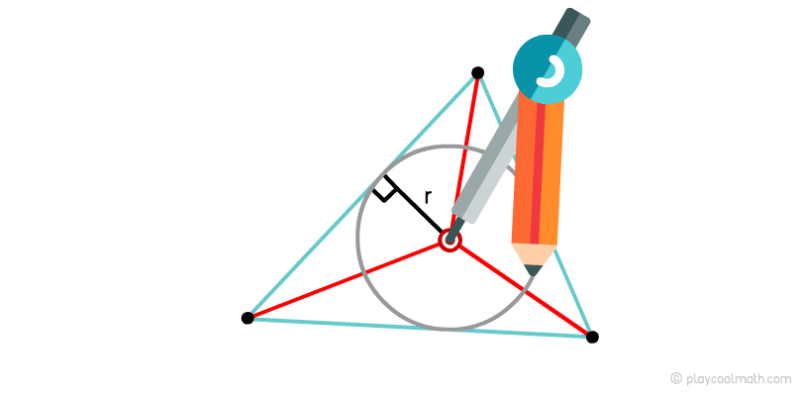
Биссектриса треугольника

Биссектриса или биссéктор треугольника – это отрезок, соединяющий вершину угла треугольника с основания вершины и делящий этот угол пополам.

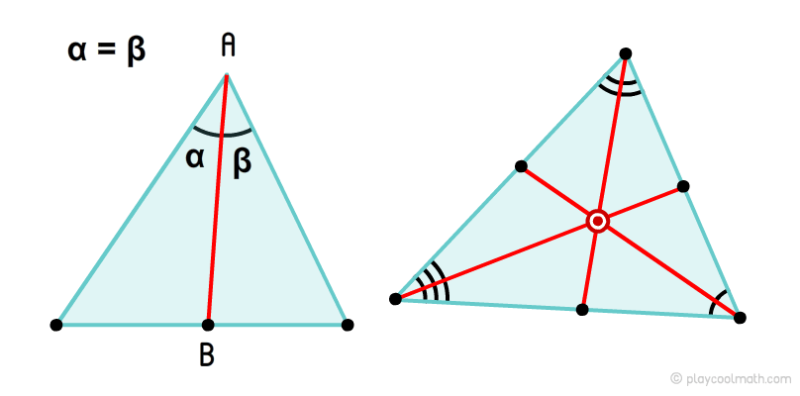
Точка, образованная пересечением биссектрис называется инцентромом.

Для того чтобы измерить угол треугольника и разбить его пополам, тебе понадобится специальная линейка – транспортир. У этой линейки есть шкала, показывающая угловую меру в градусах от центральной точки линейки.

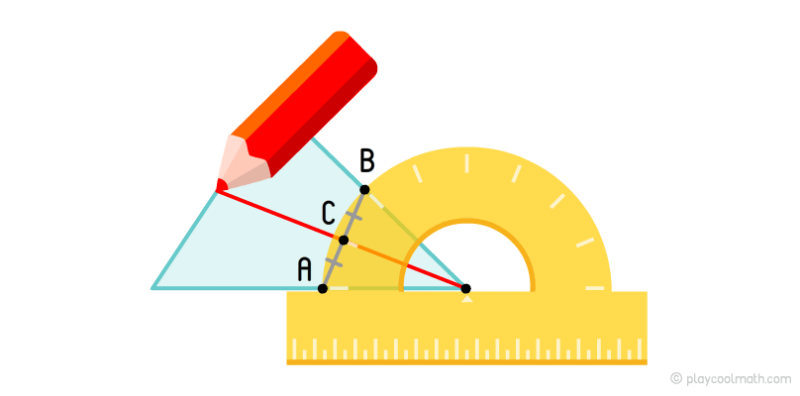
Сопоставь центральную точку линейки с вершиной так, чтобы одна сторона треугольника совпадала с основанием линейки. Найди, на какую цифру, на шкале линейки, указывает вторая сторона вершины, если ее продлить в длину. Поставь точки у значения 0 и там, где мы измерили. Обознач эти точки как A и B.

Проведи отрезок через эти точки. Визуально или с помощью линейки найди середину этого отрезка и обозначь ее как точку C. На линии, проходящей из вершины к точке C, будет лежать наша биссектриса. Повтори все действия для каждой вершины треугольника.

Медиана в алгебре и геометрии

Термин медиана используется не только в геометрии, но и в алгебре. Если с геометрией все наглядно и понятно, то в алгебре это название обозначает середину числового ряда. В качестве примера можно привести простую последовательность: 1, 3, 5, 7, 9. В этом случае число 5 будет медианой.

Алгебраическое понятие широко используется в статистике, позволяя более точно определить середину числового ряда. Среди практического применения — методы анализа различных показатели (уровень доходов определенной группы лиц, какой размер одежды или обуви чаще всего продается в магазине за конкретный период).

Где находят практическое применение этих понятий?

Понятия медианы, биссектрисы и высоты находят широкое применение в геометрических расчетах и конструкциях, а также в решении задач реальной жизни.

Медиана применяется, например, при расчете статистических данных. В статистике медиана используется для оценки центральной тенденции выборки. Она позволяет определить такое значение, при котором половина значений выборки будет больше, а половина — меньше. Это помогает сглаживать экстремальные значения и получать более объективное представление о данных.

Биссектриса находит свое применение в различных областях, включая геодезию и картографию. В геодезии она используется для измерения углов между направлениями. Например, при построении треугольников на карте, биссектриса позволяет определить угол между сторонами треугольника. Это полезно при проведении геодезических съемок и составлении карт.

Высота также находит применение в геометрических расчетах, в частности, при определении площадей фигур. Например, при измерении площади треугольника высота является одним из ключевых параметров. Она перпендикулярна основанию треугольника и позволяет разделить его на два прямоугольных треугольника, для которых можно легко найти площади и затем сложить их.

Медиана	Биссектриса	Высота
Определение центральной тенденции в статистике	Измерение углов в геодезии	Расчет площади фигур
Сглаживание экстремальных значений	Построение треугольников на карте
		Разделение треугольника на два прямоугольных треугольника

Архив записей

Архив записейВыберите месяц Ноябрь 2022 (1) Сентябрь 2022 (1) Январь 2022 (2) Сентябрь 2021 (1) Июль 2021 (1) Июнь 2021 (2) Май 2021 (1) Апрель 2021 (1) Март 2021 (1) Сентябрь 2020 (1) Август 2020 (2) Июль 2020 (2) Июнь 2020 (2) Декабрь 2019 (3) Ноябрь 2019 (4) Октябрь 2019 (3) Сентябрь 2019 (2) Май 2019 (1) Октябрь 2018 (1) Июнь 2018 (1) Апрель 2018 (1) Январь 2018 (1) Ноябрь 2017 (1) Октябрь 2017 (1) Сентябрь 2017 (2) Август 2017 (4) Июль 2017 (5) Июнь 2017 (4) Май 2017 (5) Апрель 2017 (2) Март 2017 (1) Февраль 2017 (1) Январь 2017 (3) Декабрь 2016 (1) Ноябрь 2016 (2) Октябрь 2016 (3) Сентябрь 2016 (4) Август 2016 (6) Июль 2016 (9) Июнь 2016 (4) Май 2016 (5) Апрель 2016 (6) Март 2016 (5) Февраль 2016 (8) Январь 2016 (8) Декабрь 2015 (9) Ноябрь 2015 (4) Июль 2015 (1) Март 2015 (1) Февраль 2015 (1) Январь 2015 (1) Июль 2014 (1) Июль 2013 (1) Март 2013 (2) Декабрь 2012 (1) Ноябрь 2012 (1) Сентябрь 2012 (3) Август 2012 (4) Июль 2012 (4) Июнь 2012 (4) Май 2012 (4) Апрель 2012 (5) Март 2012 (7) Февраль 2012 (8) Январь 2012 (7) Декабрь 2011 (5) Ноябрь 2011 (1)

Задача

Дано: треугольник АВС разделен на два треугольника АВМ и АСМ медианой АМ. Площадь АВС равна 80 см, площадь АВМ равна 48 см, площадь АСМ равна 66 см.

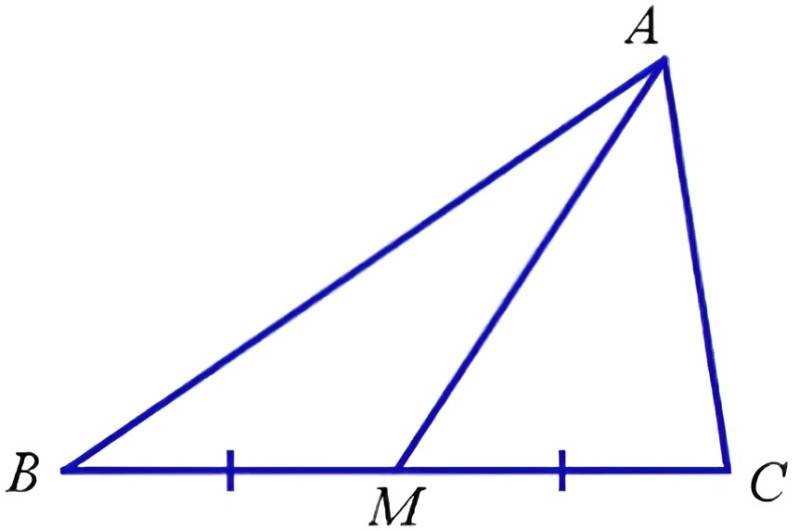
Решение:

Медиана АМ является общей стороной для малых фигур и входит в периметр основного треугольника АВС. Для составления математического уравнения обозначим медиану как Х. Теперь запишем периметры обоих малых фигур как сумму всех сторон:

Для треугольника АВМ формула периметра выглядит так: АВ + ВМ + Х = 48 см

Для треугольника АСМ получаем аналогичную формулу: АС + СМ + Х = 66 см

Составляем два уравнения с одной неизвестной (Х).

Для этого складываем обе стороны и получаем: АВ + АС + ВМ + СМ + 2Х = 114

Отрезки ВМ и СМ равны, так как АМ — это медиана. При этом они в сумме составляют сторону большого треугольника ВС.

С учетом новых данных уравнение приобретает следующий вид: АС + АВ + ВС + 2Х = 114, где АС + АВ + ВС — это площадь большого треугольника. По условию задачи она равна 80 см.

Теперь уравнение имеет такой вид: 80 + 2Х = 114

Решение очень простое: 2Х = 114 – 80, 2Х = 35, Х = 17

Пример задач

Пример 1

Пусть дан треугольник $ABC$. Доказать, что если в нем $BD$ будет и высотой и медианой, то $AB=BC$.

Доказательство

Изобразим рисунок по условию задачи (рис. 5).

Так как $BD$ является медианой, то по определению 4 будет верно равенство
$AD=DC$

Так как $BD$ является высотой, то по определению 6 будет верно равенство
$∠ADB=∠BDC=90^0$

У треугольников $ADB$ и $BDC$ сторона $BD$ будет общей, следовательно, по всему сказанному выше эти треугольники равняются по первому признаку. Но тогда и стороны $AB$ и $BC$ равны.

Пример 2

Пусть нам даны равные треугольники $ABC$ и $A’B’C’$. В них проведены высоты $BH$ и $B’H’$, соответственно. Доказать, что эти высоты в треугольниках будут равны между собой.

Доказательство.

Изобразим рисунок по условию задачи (рис. 6).

Так как данные треугольники равны, то будет верно равенство
$∠A=∠A’$

Так как $BH$ и $B’H’$ являются высотами, то по определению 6 будет верно равенство
$∠AHB=∠A’H’B’=90^0$

Из треугольника $ABC$, имеем

$∠ABH=180^0-90^0-∠A=90^0-∠A$

Из треугольника $A’B’C’$ и равенства углов $∠A$ и $∠A’$, получим

$∠A’B’H’=180^0-90^0-∠A’=90^0-∠A’=90^0-∠A=∠ABH$

По всему сказанному выше, треугольники $AHB$ и $A’B’H’$ равняются по первому признаку. Но тогда и стороны $BH$ и $B’H’$ равны.

Классификация треугольников по сторонам

Равносторонний треугольник

Равносторонний треугольник или правильный треугольник – это треугольник, у которого все стороны равны. У равностороннего треугольника все углы равны 60°.

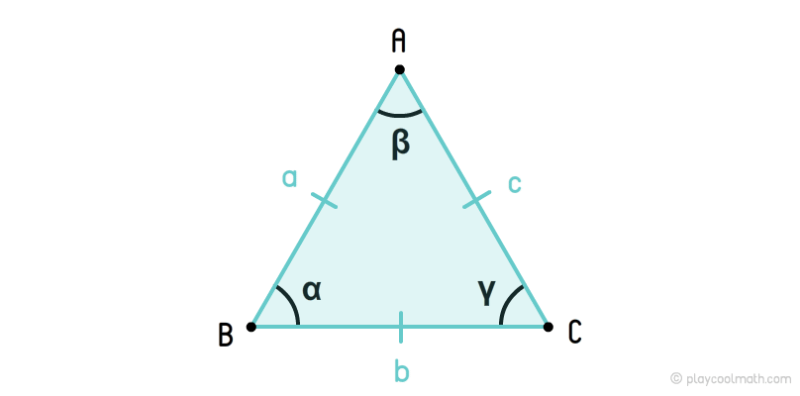
На рисунке мы обозначили стороны как a, b, c, где a = b = c. Углы обозначили как α, β, γ, где α = β = γ = 60°. Одинаковые стороны помечаются одинаковым количеством черточек. Мы пометили стороны a, b, c одной чертой. Одинаковые углы помечаются одинаковым количеством дуг. На рисунке мы все углы пометили одной дугой.

Неравносторонний треугольник

Неравносторонний треугольник – это треугольник, у которого все стороны не равны. У неравностороннего треугольника углы тоже не равны.

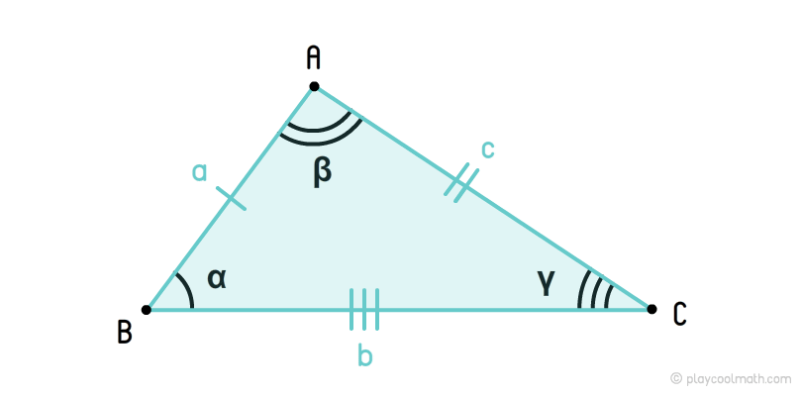
На рисунке мы обозначили стороны a, b, c, где a ≠ b ≠ c. Углы обозначили как α, β, γ, где α ≠ β ≠ γ. Мы пометили стороны a, b, c разным количеством черточек, указав что все стороны имеют разную длину. Все углы пометили разным количеством дуг, указав, что все углы имеют разные угловые меры.

Равнобедренный треугольник

Равнобедренный треугольник – это треугольник, у которого две стороны равны. Эти стороны называются боковыми или бедрами, а третья сторона называется основанием.

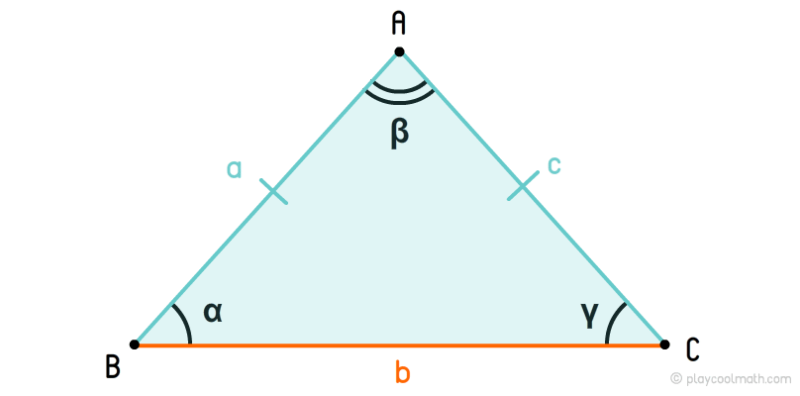
На рисунке мы обозначили боковые стороны как a, c, где a = c, а основание b, где b ≠ a и b ≠ c. У равнобедренного треугольника углы у основания равны α = γ.

Применение медианы и биссектрисы

Медиана

Медиана треугольника является линией, проходящей через один из вершин треугольника и середину противоположной стороны. В каждом треугольнике есть три медианы. Медианы пересекаются в точке, называемой центром масс или центроидом треугольника.

Медиана имеет несколько применений. Одно из них — вычисление центра масс. Центр масс является точкой баланса треугольника и может использоваться в инженерии и архитектуре для определения распределения веса или равновесия системы. Медианы также используются для решения задач о треугольниках, например, для нахождения площади треугольника или построения высот.

Биссектриса

Биссектриса треугольника является линией, проходящей через одну из вершин треугольника и делящей противоположный угол пополам. В каждом треугольнике есть три биссектрисы. Биссектрисы пересекаются в точке, называемой центром вписанной окружности треугольника.

Биссектрисы имеют различные применения. В геометрии они могут использоваться для нахождения точек пересечения с вписанными окружностями или решения задач о вписанных углах. Они также могут быть полезны при нахождении центра окружности, описанной вокруг треугольника. Вначале биссектрисы изучают в геометрии, а затем и в аналитической геометрии, где они используются для решения уравнений и систем уравнений.

Различия между медианой и биссектрисой

Медиана — это линия, которая соединяет вершину треугольника с серединой противоположной стороны. В отличие от биссектрисы, медиана делит сторону треугольника на две равные части. Точка пересечения медиан называется центроидой.

Биссектриса разделяет угол треугольника на две равные части. Она проходит через вершину угла и делит противолежащую сторону на две равные части. Биссектриса часто используется для нахождения точным серединным углов, например, при построении равнобедренных треугольников.

Таким образом, медиана и биссектриса отличаются своими характеристиками и применением в геометрии. Медиана делит сторону треугольника на две равные части и позволяет определить центроиду, а биссектриса делит угол на две равные части и используется при построении равнобедренных треугольников.

Линейные характеристики

Медиана — это отрезок, соединяющий вершину треугольника со средней точкой противолежащей стороны. Она делит каждую из сторон пополам и пересекается с другими медианами в одной точке, называемой центром тяжести.
Биссектриса — это отрезок, исходящий из вершины треугольника и разделяющий противолежащий угол на два равных угла. Она пересекается с другими биссектрисами в одной точке, называемой центром вписанной окружности.

Одним из применений медианы является нахождение центра тяжести треугольника, который является точкой пересечения медиан и таким образом делит их в отношении 2:1. Эта точка имеет свойство, что сумма квадратов расстояний от нее до вершин треугольника минимальна.

Биссектриса в свою очередь используется для нахождения центра вписанной окружности треугольника. Вписанная окружность касается сторон треугольника в точках, где биссектрисы пересекаются с ними. Центр вписанной окружности является точкой пересечения биссектрис и имеет свойство, что от него до сторон треугольника равны расстояния.

Применение в геометрии

Одно из основных применений медианы — нахождение центра тяжести треугольника. Центр тяжести — точка, в которой пересекаются все три медианы треугольника. Она имеет большое значение при решении различных задач в геометрии и механике.

Биссектриса же часто используется для построения различных фигур и решения задач. Она помогает делить углы на равные части и находить точку пересечения углов.

Таким образом, медиана и биссектриса имеют свои отличия, но их применение в геометрии широко используется для решения задач, построения фигур и нахождения важных точек треугольника.