Что изучает статистика?

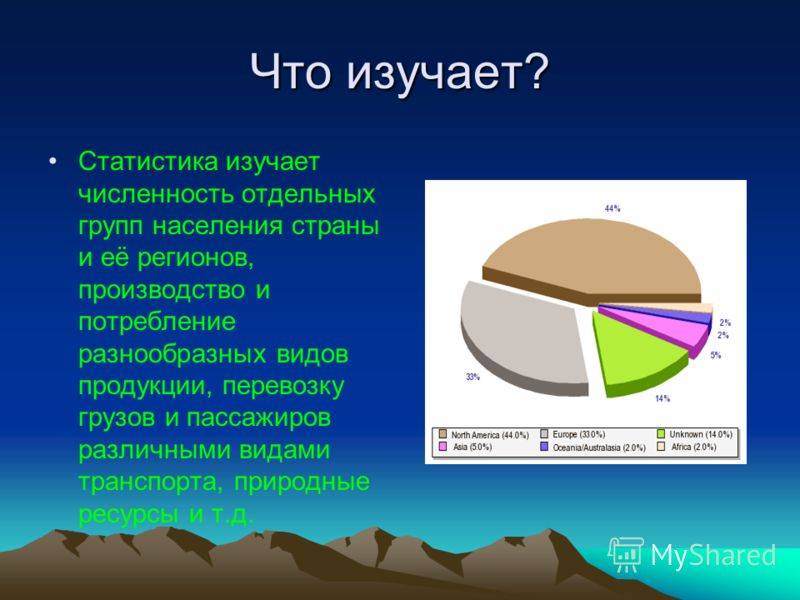
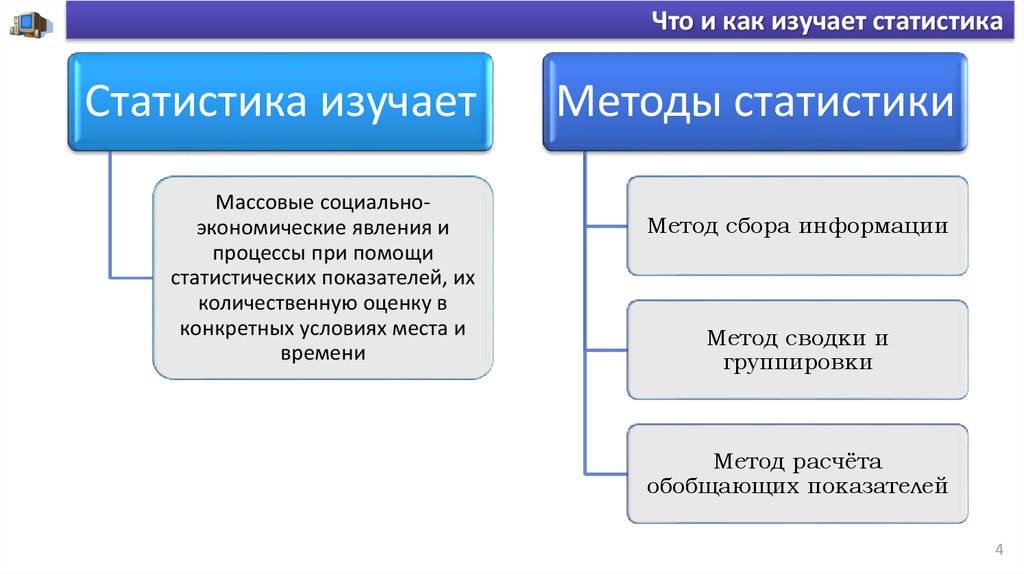
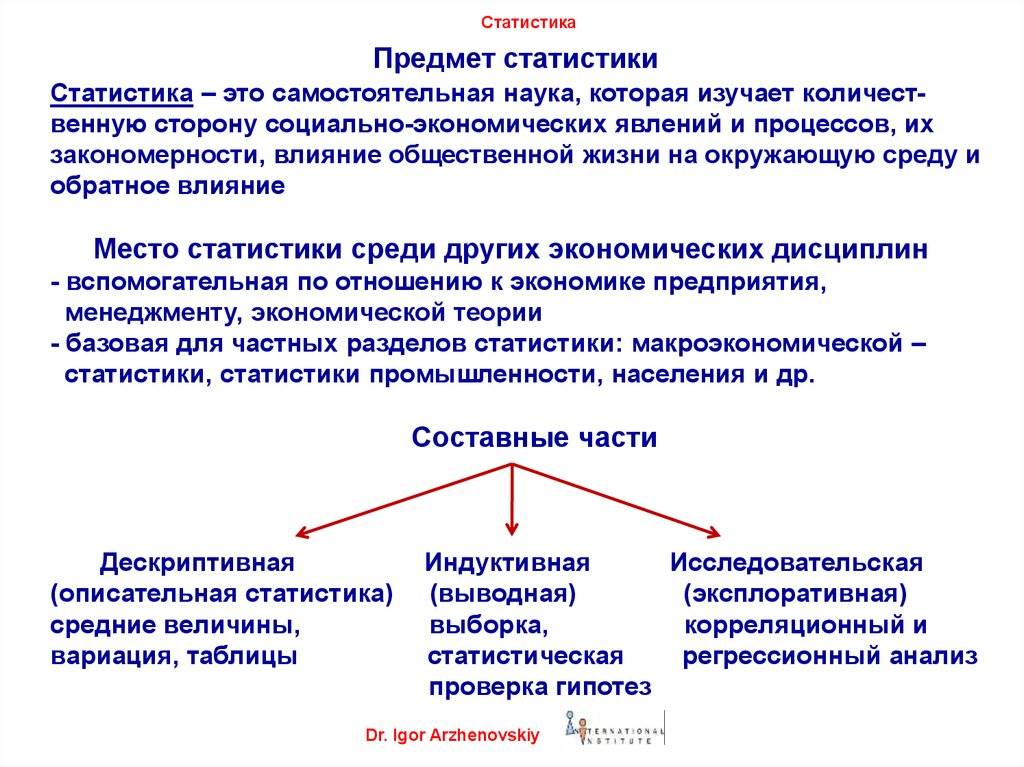
Сущность понятия «статистика» и ее экономическая сущность

Статистика — это научная дисциплина, занимающаяся исследованием социальных процессов, раскрытием их сути и роли, а также, закономерностей их протекания и взаимосвязей.

В настоящее время термин «статистика» употребляется в различных значениях. Она рассматривается в качестве научной отрасли, ориентированной на формирование системы знаний в разных областях социальной жизнедеятельности, а также, является инструментом государственного регулирования и контроля социально-экономической сферы.

Ведущими трактовками понятия «статистика», выступающими отражением ее экономической сущности, являются следующие:

1. Статистика— это сфера практической деятельности людей, связанная с процессами сбора, анализа, обработки, накопления информационных данных и их представлением в динамике. Таким образом, происходит формирование картины развития системы образования, сферы культуры, различных макроэкономических показателей и микроэкономической среды в разрезе государств и регионов, формируется представление о сфере культуры и иных социально-значимых аспектах.
2. Статистика — это наука, которая занимается разработкой технических положений и методов, используемых статистической практикой. Здесь, реализуется утверждение связи научной области статистики с ее практическим назначением. Статистика не рассматривается только в качестве научной основы. Она не только формирует теоретические аспекты процессов проведения статистических исследований, но и реализует использование норм и правил, принципов реализации статистической деятельности и обеспечивает обратную связь – на основании показателей статистической практики вносятся коррективы в положения статистической науки.
3. Статистика – это результаты статистической работы отдельных хозяйствующих субъектов, организаций специального назначения, органов государственной власти, представленные в форме статистических показателей, отчетных данных, отражающих реализацию различных процессов, сфер и направлений.

Статья: Статистика

Найди решение своей задачи среди 1 000 000 ответов

Таким образом, проведенное исследование понятия «статистика» и его экономической сущности позволяет сделать вывод о том, что статистика является инструментом познания. Благодаря данной науке открываются возможности проведения исследований в различных областях, сферах и направлениях деятельности.

Специфическими аспектами статистики выступают:

• количественное представление статистической информации разного рода;
• проведение анализа собранных и обработанных числовых данных и формулирование на его основе выводов;
• отражение текущего состояния отдельных процессов, объектов, явлений при определенных условиях их протекания и иных показателей развития.

Применение статистики в различных областях

Статистика является важным инструментом во многих областях науки, бизнеса и повседневной жизни. Она позволяет нам собирать, анализировать и интерпретировать данные, чтобы делать информированные решения и выводы. Рассмотрим некоторые области, в которых статистика широко применяется:

Медицина и здравоохранение

Статистика играет важную роль в медицине и здравоохранении. Она помогает в оценке эффективности лекарств и лечебных методов, анализе заболеваемости и смертности, прогнозировании распространения эпидемий и пандемий, а также в планировании и оценке эффективности программ общественного здравоохранения.

Экономика и финансы

Статистика является неотъемлемой частью экономики и финансов. Она используется для анализа рынков, прогнозирования экономического роста, оценки финансовой устойчивости компаний, моделирования финансовых рисков и принятия инвестиционных решений.

Социология и психология

Статистика играет важную роль в социологии и психологии. Она помогает в изучении социальных и психологических явлений, определении тенденций и паттернов поведения, анализе общественного мнения и предпочтений, а также в проведении социологических и психологических исследований.

Образование

Статистика применяется в образовании для анализа успеваемости студентов, оценки эффективности образовательных программ, определения причин неуспеваемости и разработки методов улучшения образовательного процесса.

Маркетинг и реклама

Статистика используется в маркетинге и рекламе для анализа рынка, изучения потребительского поведения, определения целевой аудитории, оценки эффективности рекламных кампаний и принятия маркетинговых решений.

Государственное управление

Статистика играет важную роль в государственном управлении. Она используется для анализа социально-экономического развития, оценки эффективности государственных программ, прогнозирования демографических изменений и разработки политики.

Это лишь некоторые области, в которых статистика применяется. Она является универсальным инструментом, который помогает нам понять и объяснить мир вокруг нас, принимать обоснованные решения и делать выводы на основе фактов и данных.

↑яРПСЙРСПЮ ЯРЮРХЯРХЙХ

б ОПНЖЕЯЯЕ ПЮГБХРХЪ ЯРЮРХЯРХЙХ ЙЮЙ МЮСЙХ БНГМХЙКХ ЯКЕДСЧЫХЕ ЯЮЛНЯРНЪРЕКЭМШЕ МЮСВМШЕ ДХЯЖХОКХМШ:

• НРПЮЯКЕБШЕ ЯРЮРХЯРХЙХ, Б ПЮЛЙЮУ ЙНРНПШУ ХГСВЮЕРЯЪ ЯСЫМНЯРЭ ЩЙНМНЛХВЕЯЙХУ ОНЙЮГЮРЕКЕИ, ХЯОНКЭГСЕЛШУ ДКЪ УЮПЮЙРЕПХЯРХЙХ ЯННРБЕРЯРБСЧЫЕИ НРПЮЯКХ ЩЙНМНЛХЙХ, Х ПЮГПЮАЮРШБЮЕРЯЪ ЛЕРНДНКНЦХЪ ХУ ХЯВХЯКЕМХЪ (ЯРЮРХЯРХЙЮ ОПНЛШЬКЕММНЯРХ, ЯЕКЭЯЙНЦН УНГЪИЯРБЮ, РПЮМЯОНПРЮ);
• ЩЙНМНЛХВЕЯЙЮЪ ЯРЮРХЯРХЙЮ, Б ЙНРНПНИ ПЮЯЙПШБЮЕРЯЪ  ЯСЫМНЯРЭ Х ЛЕРНДНКНЦХЪ ХЯВХЯКЕМХЪ ОНЙЮГЮРЕКЕИ, ХЯОНКЭГСЕЛШУ ОПХ ЯРЮРХЯРХВЕЯЙНЛ ХГСВЕМХХ ЩЙНМНЛХЙХ Б ЖЕКНЛ. щЙНМНЛХВЕЯЙЮЪ ЯРЮРХЯРХЙЮ РЕЯМН ЯБЪГЮМЮ ЯН ЯРЮРХЯРХЙНИ НРДЕКЭМШУ НРПЮЯКЕИ, МЮ ЙНРНПСЧ БНГКНФЕМЮ ГЮДЮВЮ ОНДПНАМНЦН НОХЯЮМХЪ Х ЮМЮКХГЮ ТСМЙЖХНМХПНБЮМХЪ ЯННРБЕРЯРБСЧЫХУ НРПЮЯКЕИ. цПЮМХЖЮ ЛЕФДС ЩЙНМНЛХВЕЯЙНИ ЯРЮРХЯРХЙНИ Х НРПЮЯКЕБШЛХ ЯРЮРХЯРХЙЮЛХ МНЯХР Б ГМЮВХРЕКЭМНИ ЛЕПЕ СЯКНБМШИ УЮПЮЙРЕП. щЙНМНЛХВЕЯЙЮЪ ЯРЮРХЯРХЙЮ ХЯОНКЭГСЕР ДЮММШЕ НРПЮЯКЕБШУ ЯРЮРХЯРХЙ ДКЪ ОНКСВЕМХЪ НАНАЫЮЧЫХУ ОНЙЮГЮРЕКЕИ. нЯМНБМШЕ НОПЕДЕКЕМХЪ Х ЙКЮЯЯХТХЙЮЖХХ ЩЙНМНЛХВЕЯЙНИ ЯРЮРХЯРХЙХ Х НРПЮЯКЕБШУ ЯРЮРХЯРХЙ ВЕРЙН ЯНЦКЮЯНБЮМШ ДПСЦ Я ДПСЦНЛ. пЮГПЮАЮРШБЮЪ ЛЕРНДШ ХЯВХЯКЕМХЪ РЕУ ХКХ ХМШУ ОНЙЮГЮРЕКЕИ, ЩЙНМНЛХВЕЯЙЮЪ ЯРЮРХЯРХЙЮ НОХПЮЕРЯЪ МЮ ХМЯРПСЛЕМРЮПХИ РЕНПХХ ЯРЮРХЯРХЙХ;
• НАЫЮЪ РЕНПХЪ ЯРЮРХЯРХЙХ (ХКХ РЕНПХЪ ЯРЮРХЯРХЙХ), ЙНРНПЮЪ ПЮГПЮАЮРШБЮЕР ЯРЮРХЯРХВЕЯЙСЧ ЛЕРНДНКНЦХЧ, ЯРЮРХЯРХВЕЯЙХЕ ЛЕРНДШ, ХЯОНКЭГСЕЛШУ ЙЮЙ Б НРПЮЯКЕБШУ ЯРЮРХЯРХЙЮУ, РЮЙ Х Б ЩЙНМНЛХВЕЯЙНИ ЯРЮРХЯРХЙЕ;
• ЛЮРЕЛЮРХВЕЯЙЮЪ ЯРЮРХЯРХЙЮ,  Р.Е. МЮСЙЮ, ПЮГПЮАЮРШБЮЧЫЮЪ ЯОЕЖХЮКЭМШИ ЛЮРЕЛЮРХВЕЯЙХИ ЮООЮПЮР ДКЪ ЯХЯРЕЛЮРХГЮЖХХ Х ХЯОНКЭГНБЮМХЪ ЯРЮРХЯРХВЕЯЙХУ ДЮММШУ Я ЖЕКЭЧ ОНКСВЕМХЪ МЮСВМШУ Х ОПЮЙРХВЕЯЙХУ БШБНДНБ. дЮММШИ ПЮГДЕК ЯРЮРХЯРХЙХ МЕПЮГПШБМН ЯБЪГЮМ Я ЛЮРЕЛЮРХЙНИ. нМ ЬХПНЙН НОХПЮЕРЯЪ МЮ РЕНПХЧ БЕПНЪРМНЯРЕИ Х ДПСЦХЕ ПЮГДЕКШ ЛЮРЕЛЮРХЙХ

Для чего используется математическая статистика

• Для правильного сбора и обработки статистических данных.
• Для описания больших массивов данных, которые выражают какие-либо явления: от результатов физического эксперимента до соцопроса или информации о посещениях сайта.
• Для представления данных в форме графиков или таблиц.
• Для прогнозирования и проверки гипотез — предположений, которые можно подтвердить или опровергнуть с помощью статистических данных.
• Для избавления от ошибок, которые могут быть связаны с неправильным сбором, обработкой или интерпретацией сведений.
• Для расчета возможных отклонений результата от истины.

Расчет общей дисперсии

x	f	xf	x2	x2f
10	50	50	100	500
11	150	165	121	1815
13	50	65	169	845
15	50	75	225	1125
18	70	126	324	2268
20	30	60	400	1200
	40	541		7753

2. Расчет
дисперсии по первой группе

x	f	xf	x2	x2f
10	50	50	100	500
11	150	165	121	1815
13	50	65	169	845
	25	280		3160

3. Расчетдисперсии по второй группе

x	f	xf	x2	x2f
15	50	75	225	1125
18	70	126	324	2268
20	30	60	400	1200
	15	261		4593

4. Расчет
межгрупповой дисперсии

11,2	25	-2,325	5,405	135,140
17,4	15	3,875	15,015	225,234
	40			360,375

5. Расчет
средней из индивидуальных дисперсий

Эмпирическое корреляционное
отношение (ЭКО)

На основании правила сложения дисперсий вычисляется
эмпирическое корреляционное отношение (ЭКО), которое равно квадратному корню из
отношения межгрупповой дисперсии к общей:

Такой порядок вычисления обусловлен
разложением общей вариации на вариацию, зависящую от фактора, положенного в
основу группировки (в нашем примере – повышение и неповышение квалификации),
которая численно равна межгрупповой дисперсии, и общую вариацию.

Межгрупповая дисперсия составляет часть общей
дисперсии и складывается под влиянием только одного группировочного фактора.
Именно поэтому подкоренное выражение показывает долю вариации за счет
группировочного признака.

ЭКО изменяется в переделах от нуля до единицы. Чем
ближе его значение к единице, тем большая доля вариации падает на
группировочный признак.

В нашем случае

Некоторые математические свойства
дисперсий

(1)При вычитании из всех
значений признака некоторой постоянной величины дисперсия не изменится.

(2)При сокращении всех
значенийна постоянный
множительдисперсия уменьшится
враз.

(3)Средний квадрат отклонений
значений признакаот постоянной
произвольной величиныбольше дисперсии
признакана квадрат разности между
средней арифметическойи постоянной
величиной.

На основании
свойств дисперсии ее можно подсчитать способом отсчета от условного нуля и способом
моментов.

Интервал
90-100	95	2	190	-30	-3	-6	9	18
100-110	105	6	630	-20	-2	-12	4	24
110-120	115	8	920	-10	-1	-8	1	8
120-130	125	18	2 250
130-140	135	5	675	10	1	5	1	5
140-150	145	4	580	20	2	8	4	16
150-160	155	3	465	30	3	9	9	27
160-170	165	2	330	40	4	8	16	32
170-180	175	2	350	50	5	10	25	50
		50	6 390			14		180

Понятие индексов

В статистике под индексом понимается относительная
величина (показатель), выражающая изменение сложного экономического явления во
времени, в пространстве или по сравнению с планом. В связи с этим различают
динамические, территориальные индексы, а также индексы выполнения плана.

Многие
общественные явления состоят из непосредственно несопоставимых явлений, поэтому
основной вопрос – это вопрос сопоставимости сравниваемых явлений.

К какому бы
экономическому явлению ни относились индексы, чтобы рассчитать их, необходимо
сравнивать различные уровни, которые относятся либо к различным периодам
времени, либо к плановому заданию, либо к различным территориям. В связи с этим
различают базисный период (период, к
которому относится величина, подвергаемая сравнению) и отчетный период (период, к которому относится сравниваемая
величина)

При исчислении важно правильно выбрать период, принимаемый за базу
сравнения

Индексы могут
относиться либо к отдельным элементам сложного экономического явления, либо ко
всему явлению в целом.

Индивидуальные индексы

Показатели,
характеризующие изменение более или менее однородных объектов, входящих в состав
сложного явления, называются индивидуальными
индексами – i_x.

p – цена q – количество t – время T – численность f – з/п F – фонд з/п S – посевная площадь y – урожайность z – себестоимость

Индекс получает
название по названию индексируемой величины.

В большинстве случаев в числителе стоит текущий уровень, а в
знаменателе – базисный уровень. Исключением является индекс покупательной способности рубля.

Индексы измеряются либо в
виде процентов (%), либо в виде коэффициентов.

Сводные индексы

Сложные
явления, для которых рассчитывается сводный индекс, отличаются той
особенностью, что элементы, их составляющие, неоднородны и, как правило,
несоизмеримы друг с другом. Поэтому сопоставление простых сумм этих элементов
невозможно. Сопоставимость может быть достигнута различными способами:

(1)сложные явления могут быть
разбиты на такие простые элементы, которые в известной степени являются
однородными;

(2)сравнение по стоимости, без
разбиения на отдельные элементы.

Цель теории индексов –
изучение способов получения относительных величин, используемых для расчета общего
изменения ряда разнородных явлений.

Товар	Базисный	Отчетный
1
2
. . .
n

↑мЕПЮГПЕЬЕММШЕ ОПНАКЕЛШ Х ОПХНПХРЕРМШЕ МЮОПЮБКЕМХЪ

й ВХЯКС МЕПЮГПЕЬЕММШУ ОПНАКЕЛ  Х ОПХНПХРЕРМШУ МЮОПЮБКЕМХИ ЯРЮРХЯРХВЕЯЙНИ МЮСЙХ НРМНЯЪРЯЪ:

1. яНБЕПЬЕМЯРБНБЮМХЕ ЛЕФДСМЮПНДМШУ ЯРЮРХЯРХВЕЯЙХУ ЯРЮМДЮПРНБ Х ЙКЮЯЯХТХЙЮЖХИ, Х НАЕЯОЕВЕМХЕ ЯНОНЯРЮБХЛНЯРХ МЮЖХНМЮКЭМШУ ЯРЮМДЮПРНБ Я ЛЕФДСМЮПНДМШЛХ. пЮГПЮАНРЙЮ ЙКЮЯЯХТХЙЮРНПНБ ХМБЕЯРХЖХНММШУ, ОПНЛЕФСРНВМШУ Х ОНРПЕАХРЕКЭЯЙХУ РНБЮПНБ; СЯКСЦ БН БМЕЬМЕЩЙНМНЛХВЕЯЙНИ ДЕЪРЕКЭМНЯРХ; МЕОПНХГБЕДЕММШУ ЮЙРХБНБ;ТХМЮМЯНБШУ ЮЙРХБНБ; ЖЕММНЯРЕИ.

2. пЮГБХРХЕ ЯХЯРЕЛШ ЛЮЙПНЩЙНМНЛХВЕЯЙХУ ОНЙЮГЮРЕКЕИ, БЙКЧВЮЧЫЕИ ОНБШЬЕМХЕ ЙЮВЕЯРБЮ ПЮЯВЕРНБ ОНЙЮГЮРЕКЕИ ямя Б ЯННРБЕРЯРБХЕ Я ЛЕРНДНКНЦХВЕЯЙХЛХ ОПХМЖХОЮЛХ ямя ннм 2008.

3. пЮГПЮАНРЙЮ ОНЙЮГЮРЕКЕИ ямя ОН ХМЯРХРСЖХНМЮКЭМШЛ ЯЕЙРНПЮЛ ЩЙНМНЛХЙХ.

4. яНБЕПЬЕМЯРБНБЮМХЕ ЛЕРНДНКНЦХХ ЯРЮРХЯРХВЕЯЙНИ НЖЕМЙХ НАЗЕЛНБ ЯЙПШРНИ, МЕТНПЛЮКЭМНИ Х МЕГЮЙНММНИ ЩЙНМНЛХВЕЯЙНИ ДЕЪРЕКЭМНЯРХ Я ЖЕКЭЧ ЕЦН НРПЮФЕМХЪ Б ямя.

5. лЕРНДНКНЦХЪ ПЮЯВЕРЮ ДХМЮЛХЙХ ОНЙЮГЮРЕКЕИ ямя.

6. хЯОНКЭГНБЮМХЕ ДЮММШУ МЮЖХНМЮКЭМШУ ЯВЕРНБ ДКЪ ЩЙНМНЛХВЕЯЙНЦН ЮМЮКХГЮ, ПЮГПЮАНРЙХ ЩЙНМНЛХВЕЯЙНИ ОНКХРХЙХ Х ОПНЦМНГНБ ЯНЖХЮКЭМН-ЩЙНМНЛХВЕЯЙНЦН ПЮГБХРХЪ ЯРПЮМШ МЮ ДНКЦНЯПНВМШИ, ЯПЕДМЕЯПНВМШИ Х ЙПЮРЙНЯПНВМШИ ОЕПХНДШ. 

7. йНМЖЕОЖХЪ ХГЛЕПЕМХЪ ХМБЕЯРХЖХИ, ЯННРБЕРЯРБСЧЫЮЪ ЛЕРНДНКНЦХВЕЯЙХЛ РПЕАНБЮМХЪЛ ямя Х НАКЕЦВЮЧЫЮЪ ОПНБЕДЕМХЕ ЛЕФДСМЮПНДМШУ ЯНОНЯРЮБКЕМХИ.

8. яРЮРХЯРХВЕЯЙНЕ МЮАКЧДЕМХЕ ГЮ ДБХФЕМХЕЛ ЖЕММШУ АСЛЮЦ ДКЪ НАЕЯОЕВЕМХЪ ОНРПЕАМНЯРЕИ ЯХЯРЕЛШ МЮЖХНМЮКЭМШУ ЯВЕРНБ.

9. пЮГПЮАНРЙЮ ЯХЯРЕЛШ ЯРЮРХЯРХВЕЯЙХУ ОНЙЮГЮРЕКЕИ ДКЪ НАЕЯОЕВЕМХЪ ЙНЛОКЕЙЯМНИ ХМТНПЛЮЖХХ НА СПНБМЕ, ЙЮВЕЯРБЕ Х СЯКНБХЪУ ФХГМХ МЮЯЕКЕМХЪ, НЖЕМЙЕ ЕЦН ЯНЖХЮКЭМНИ ГЮЫХРШ Б ЯННРБЕРЯРБХХ Я ЖЕКЪЛХ, ОНЯРЮБКЕММШЛХ Б дЕЙКЮПЮЖХХ РШЯЪВЕКЕРХЪ ннм, ЙНРНПЮЪ ЪБКЪЕРЯЪ НДМХЛ ХГ НЯМНБМШУ ЙПХРЕПХЕБ ПЮГБХРХЪ ЯНЖХЮКЭМНИ ЯРЮРХЯРХЙХ.

10.  пЮЯВЕР ХМДЕЙЯЮ ЯРНХЛНЯРХ ФХГМХ.

11. лЕРНДШ Х ЛНДЕКХ ЯЕГНММНЦН ЯЦКЮФХБЮМХЪ БПЕЛЕММШУ ПЪДНБ ДЕКНБНИ ЮЙРХБМНЯРХ НПЦЮМХГЮЖХИ.

12. яХЯРЕЛЮ ЯРЮРХЯРХВЕЯЙХУ ОНЙЮГЮРЕКЕИ Х ЛЕРНДНКНЦХЪ ХУ ТНПЛХПНБЮМХЪ ОН НРДЕКЭМШЛ МЮОПЮБКЕМХЪЛ ОПХПНДННУПЮММНИ ДЕЪРЕКЭМНЯРХ, БЙКЧВЮЪ ЯХЯРЕЛС ЮЦПНЩЙНКНЦХВЕЯЙХУ ОНЙЮГЮРЕКЕИ.

13. лЕРНДШ ПЕРПНЯОЕЙРХБМНИ ЙНППЕЙРХПНБЙХ ДХМЮЛХВЕЯЙХУ ПЪДНБ ЩЙНМНЛХВЕЯЙХУ ОНЙЮГЮРЕКЕИ.

14. яНБЕПЬЕМЯРБНБЮМХЕ ЛЕРНДНКНЦХХ ТНПЛХПНБЮМХЪ Х НЖЕМЙХ БШАНПЙХ УНГЪИЯРБСЧЫХУ ЯСАЗЕЙРНБ ОПХ ОПНБЕДЕМХХ ЯРЮРХЯРХВЕЯЙХУ МЮАКЧДЕМХИ ГЮ ПЮГКХВМШЛХ ЮЯОЕЙРЮЛХ ХУ ЩЙНМНЛХВЕЯЙНИ ДЕЪРЕКЭМНЯРХ.

15. лЕРНДНКНЦХЪ ПЮЯВЕРЮ ХМДЕЙЯЮ ОПНЛШЬКЕММНЦН ОПНХГБНДЯРБЮ, БЙКЧВЮЪ ЯЕГНММСЧ ЙНППЕЙРХПНБЙС ДХМЮЛХВЕЯЙХУ  ПЪДНБ.   

16. нПЦЮМХГЮЖХЪ Х БЕДЕМХЕ ЛНМХРНПХМЦЮ ОНЙЮГЮРЕКЕИ ДЕЪРЕКЭМНЯРХ ЯСАЗЕЙРНБ АЧДФЕРМНЦН ОКЮМХПНБЮМХЪ.

17. пЮГПЮАНРЙЮ ЛЕРНДНКНЦХХ НЖЕМЙХ НАЗЕЛЮ Х ЯРПСЙРСПШ ЯНБНЙСОМШУ ГЮРПЮР МЮ НАПЮГНБЮМХЕ ГЮ ЯВЕР БЯЕУ ХЯРНВМХЙНБ ТХМЮМЯХПНБЮМХЪ, БЙКЧВЮЪ МЕМЮАКЧДЮЕЛШЕ ТХМЮМЯНБШЕ ОНРНЙХ.

18. тНПЛХПНБЮМХЕ ЙЮВЕЯРБЕММН МНБНИ ЯРЮРХЯРХВЕЯЙНИ ХМТНПЛЮЖХХ, НАЕЯОЕВХБЮЧЫЕИ ЛНМХРНПХМЦ МЮСВМНЦН ОНРЕМЖХЮКЮ ЯРПЮМШ Х ЕЦН ХЯОНКЭГНБЮМХЪ Я ЩРНИ ЖЕКЭЧ МЕНАУНДХЛН ПЮГПЮАНРЮРЭ ЛЕРНДНКНЦХЧ Х ЯРЮРХЯРХВЕЯЙХИ ХМЯРПСЛЕМРЮПХИ ЙНЛОКЕЙЯМНИ ЯРЮРХЯРХВЕЯЙНИ НЖЕМЙХ ПЕГСКЭРЮРНБ ДЕЪРЕКЭМНЯРХ МЮСВМШУ НПЦЮМХГЮЖХИ.

19. пЮГПЮАНРЙЮ ЯОЕЖХЮКХГХПНБЮММШУ ОПНЦПЮЛЛ ХГЛЕПЕМХЪ ОПНЖЕЯЯНБ ЦКНАЮКХГЮЖХХ МЮСВМШУ ХЯЯКЕДНБЮМХИ Х ПЮГПЮАНРНЙ.

20. тНПЛХПНБЮМХЕ ЯХЯРЕЛШ ОНЙЮГЮРЕКЕИ ХММНБЮЖХНММНИ ДЕЪРЕКЭМНЯРХ УНГЪИЯРБСЧЫХУ ЯСАЗЕЙРНБ, ПЮГПЮАНРЙЮ ЛЕРНДНКНЦХХ ХЯВХЯКЕМХЪ ЮЦПЕЦЮРМНЦН ХМДХЙЮРНПЮ ПЕГСКЭРЮРХБМНЯРХ ХММНБЮЖХНММНИ ДЕЪРЕКЭМНЯРХ.

21. пЮГПЮАНРЙЮ ЛЕРНДНКНЦХВЕЯЙХУ ОНДУНДНБ Й ЯРЮРХЯРХВЕЯЙНЛС ЮМЮКХГС ХММНБЮЖХНММШУ ЙКЮЯРЕПНБ, БЙКЧВЮЪ ЮМЮКХГ ХУ ПЮГБХРХЪ (Б ВЮЯРМНЯРХ, НЯНАШУ ЩЙНМНЛХВЕЯЙХУ ГНМ Х МЮСЙНЦПЮДНБ), БШЪБКЕМХЕ РЕППХРНПХИ, НАКЮДЮЧЫХУ МЮСВМН-РЕУМХВЕЯЙХЛ Х ХММНБЮЖХНММШЛ ОНРЕМЖХЮКНЛ БШУНДЮ МЮ ЛХПНБШЕ ПШМЙХ МЮСЙНЕЛЙНИ ОПНДСЙЖХХ.

22. яНГДЮМХЕ ЛЕРНДНКНЦХВЕЯЙНИ НЯМНБШ ДКЪ НПЦЮМХГЮЖХХ ЯРЮРХЯРХВЕЯЙНЦН МЮАКЧДЕМХЪ ГЮ КНЦХЯРХВЕЯЙХЛХ ЖЕМРПЮЛХ Х НОЕПЮРНПЮЛХ.

23. яНБЕПЬЕМЯРБНБЮМХЕ ЛЕРНДНКНЦХХ ПЮЯВЕРЮ ЯБНДМНЦН ХМДЕЙЯЮ ОНРПЕАХРЕКЭЯЙХУ ЖЕМ.

24. пЮЯВЕР ОНЙЮГЮРЕКЕИ АЮГНБНИ ХМТКЪЖХХ.

25. пЮГПЮАНРЙЮ ЯХЯРЕЛШ ОНЙЮГЮРЕКЕИ Х ЛЕРНДНКНЦХХ ЯРЮРХЯРХВЕЯЙНЦН МЮАКЧДЕМХЪ ДКЪ ТНПЛХПНБЮМХЪ НТХЖХЮКЭМНИ ЯРЮРХЯРХВЕЯЙНИ ХМТНПЛЮЖХХ НА НАЗЕЛЮУ ЩКЕЙРПНММНИ РНПЦНБКХ.

Основные понятия и термины в статистике

Популяция

Популяция в статистике — это полный набор всех элементов, о которых мы хотим собрать информацию. Например, если мы исследуем рост студентов в университете, то популяцией будет являться весь студенческий корпус.

Выборка

Выборка — это подмножество элементов из популяции, которое мы выбираем для исследования. Выборка должна быть представительной, то есть отражать характеристики популяции. Например, если мы выбираем случайную группу студентов из университета, то это будет наша выборка.

Параметр

Параметр — это числовая характеристика популяции. Например, средний рост всех студентов в университете или процент студентов, которые занимаются спортом. Параметры обычно обозначаются греческими буквами, такими как μ (мю) для среднего значения или π (пи) для процента.

Переменная

Переменная — это характеристика, которую мы измеряем у каждого элемента выборки. Например, рост студентов или количество часов, которые они уделяют учебе. Переменные могут быть количественными (например, рост в сантиметрах) или качественными (например, пол или цвет волос).

Распределение

Распределение — это способ представления данных о переменной. Распределение может быть симметричным или асимметричным, иметь пик или быть равномерным. Например, распределение роста студентов может быть нормальным, симметричным и иметь пик вокруг среднего значения.

Среднее значение

Среднее значение — это сумма всех значений переменной, деленная на количество значений. Среднее значение является одной из основных мер центральной тенденции и обозначается как X̄ (читается «икс черта»). Например, среднее значение роста студентов может быть 170 см.

Дисперсия и стандартное отклонение

Дисперсия и стандартное отклонение — это меры разброса данных вокруг среднего значения. Дисперсия — это среднее значение квадратов отклонений от среднего значения, а стандартное отклонение — это квадратный корень из дисперсии. Они обозначаются как σ (сигма) для популяции и S (эс) для выборки.

Корреляция

Корреляция — это мера степени связи между двумя переменными. Корреляция может быть положительной (когда значения двух переменных изменяются в одном направлении), отрицательной (когда значения двух переменных изменяются в противоположных направлениях) или нулевой (когда нет связи между переменными).

Гипотеза и статистическая значимость

Гипотеза — это предположение о свойствах популяции, которое мы хотим проверить на основе выборки. Статистическая значимость — это вероятность того, что различия между выборками являются реальными и не случайными. Для проверки гипотезы используются статистические тесты.

Это лишь некоторые из основных понятий и терминов в статистике. Понимание этих терминов поможет вам лучше понять и анализировать данные, проводить исследования и делать обоснованные выводы.

Что такое статистика?

С другой стороны, статистика (не путать со статистикой (ами)) — это свойство выборки. Как указано в предыдущем примере, вместо работы с полной совокупностью мы работаем с выборками, поэтому числовое значение называется статистикой выборки.

Надеюсь, теперь у вас есть приличное представление о том, что такое совокупность, выборка, статистика и параметры. Давайте взглянем на другое понятие, с которым мы все слишком хорошо знакомы: «Данные».

Данные, как следует из этого термина, представляют собой фактическую информацию. То есть, это передает нам сообщение. Однако его можно разделить на две категории:

1. Количественные данные.
2. Качественные данные.

С какими понятиями работает статистика

Генеральная совокупность 

Совокупность всех потенциально возможных вариантов, которые можно получить при одинаковых условиях. Измерить генеральную совокупность нельзя, ее размер стремится к бесконечности. Но математическая статистика использует методы, которые помогают понять, как описать ее, — для этого используется выборка.

Выборка

Данные, которые получены при наблюдениях. Размер выборки конечен и ограничен критериями — методами отбора. Таким образом выбирают множество вариантов из генеральной совокупности, по которым в теории можно сделать вывод о целом. Например, если генеральная совокупность — мнение абсолютно всех людей по вопросу, то выборка — результаты опроса по нему.

Репрезентативность

Понятие, которое говорит, насколько показательна выборка, реалистично ли в ней распределены варианты. Выборка считается репрезентативной, если в ней учтено множество параметров и она достоверно отражает генеральную совокупность.

Например, если в выборку попали только пожилые люди, то она не будет репрезентативной для оценки всех возрастных групп. А если изучалась старшая возрастная группа, то генеральной совокупностью будут все пожилые. В этом случае выборка может оказаться репрезентативной.

Репрезентативность обычно получают с помощью рандомизации — объекты или людей для исследования отбирают из генеральной совокупности случайным образом. Так в выборке получится множество разнообразных вариантов. Если же это невозможно, к репрезентативности стараются приблизиться другими способами.

Станьте дата-сайентистом и решайте амбициозные задачи с помощью нейросетей

Подробнее

Распределение

Показатель часто описывают через математические формулы. Он показывает частоту, с которой в выборке встречаются разные варианты. В результате можно сделать вывод о том, каких вариантов данных больше, каких меньше — что больше или меньше распространено внутри выборки. Если она репрезентативная, это поможет сделать выводы и о генеральной совокупности.

Визуализация

Чтобы результаты воспринимались легче, их визуализируют. Обычно строят гистограммы распределения — диаграммы со столбцами, размер которых различается в зависимости от значения. Но применяют и другие виды визуализации: точечные графики, круговые диаграммы и так далее.

Числовые характеристики 

Распределения обычно недостаточно, чтобы сделать подробные выводы. Поэтому у вариантов внутри выборки есть ряд характеристик, которые нужны для большей наглядности. Это, например:

Среднее арифметическое

— усредненное значение среди всех показателей.

Медиана

— значение, которое находится посередине распределения, то есть фактическое среднее.

Мода

— значение, которое встречается в выборке чаще всего.

Размах

— разница между минимальным и максимальным значением.

Дисперсия

— отклонение значений от среднего арифметического.

Коэффициент вариации

— значение, которое показывает рассеяние результатов в процентах.

Погрешность

Данные не могут быть стопроцентно точными, поэтому в математической статистике учитывается погрешность — это отклонение имеющихся результатов от объективно реальных. Она помогает понять, насколько точен анализ.

Что такое Качественные данные?

Это виды данных, которые представляют категории или группы данных. Они также известны как категориальные данные. Обычно они записываются в виде текста. Это могут быть характеристики, имена или что угодно еще.

Распространенным примером является имя человека, породы собак и так далее. Однако есть некоторые данные, которые кажутся числовыми, но кодируются как категориальные.

Например, предположим, вы захотели сгруппировать определенную группу людей по их возрасту и обнаружили, что самый низкий и самый высокий возраст — 10 и 60 лет соответственно. Затем вы разделили возраст на 5 категорий (10-20, 21-30, 31-40, 41-50, 51-60) и присвоил числовые значения каждой из этих категорий, где 1 представляет 10-20, 2 представляет 21-30 и так далее.

В этой ситуации числовые значения будут обрабатываться как категориальные данные, а не количественные. По мере развития вашей карьеры в области обработки данных вы научитесь работать с категориальными данными.

Теперь вы знаете категории данных. Количественные и качественные данные могут обрабатываться в статистике с использованием этих уровней измерения. Данные в статистике могут быть классифицированы на 4 уровня измерения, которые являются:

1. Номинальные данные шкалы
2. Данные порядковой шкалы
3. Данные интервальной шкалы
4. Данные шкалы коэффициентов

Качественные данные могут быть измерены с помощью:

Данные номинальной шкалы: Это тип категориальных данных, которые не имеют упорядоченного смысла. То есть они не могут быть упорядочены.

Каждый фрагмент данных представляет собой отдельную единицу. Примером таких категориальных данных является цвет. Не очень идеально ставить синий цвет выше желтого. При работе с номинальными данными каждая точка данных должна обрабатываться как отдельная единица.

Данные порядковой шкалы: Данные порядковой шкалы состоят из упорядоченных категориальных данных. Когда данные ранжируются, в них возникает ощущение порядка. Примером этого являются такие ответы на опрос, как «отлично», «хорошо», «удовлетворительно» и «неудовлетворительно». Имеет смысл ставить превосходство выше добра.

Количественные данные могут быть измерены с помощью:

Данные интервальной шкалы: Это числовые данные с упорядочением, которые могут быть измерены (например, найти разницу между данными). Показания на температурной шкале являются примером интервальных данных.

Например, вы можете измерить разницу между 4 и 10 градусами Цельсия, а 10 градусов — это больше, чем 4 градуса. Однако для данных интервальной шкалы существуют два исключения:

1. У него нет начальной точки (то есть он не начинается с нуля, и у вас может быть значение температуры ниже нуля).
2. Вы не можете вычислить их соотношение: например, нет никакой логики утверждать, что 4 раза по 20 градусов Цельсия равны 80 градусам Цельсия.

Данные шкалы отношения: Это числовые данные, которые обладают свойствами данных интервальной шкалы (то есть их можно упорядочивать и измерять), но также устраняют исключение данных интервальной шкалы (у них есть отправная точка, а также вы можете найти соотношение между ними).

Примером может служить оценка в 20, 68, 90 или 80 баллов. Мы можем упорядочить его, измерить и найти соотношение между значениями. Имеет смысл сказать, что оценка 80 в 4 раза лучше, чем оценка 20.

Теперь, когда мы рассмотрели основы данных, давайте посмотрим, как первая категория статистики (описательная статистика) может быть применена к данным.

Как указывалось ранее, описательная статистика требует суммирования данных либо в числовом, либо в графическом виде. Давайте взглянем на некоторые из наиболее типичных числовых и графических сводок, с которыми вы столкнетесь при регулярной работе с данными.

Ошибки и искажения в статистике

В статистике существуют различные ошибки и искажения, которые могут возникнуть при сборе, обработке и анализе данных. Понимание этих ошибок и искажений является важным для получения точных и надежных результатов.

Ошибки выборки

Ошибки выборки возникают, когда выборка, используемая для анализа, не является представительной для всей генеральной совокупности. Это может произойти, если выборка слишком мала или неслучайна. Например, если проводится опрос среди студентов университета, но не учитываются студенты других университетов, результаты могут быть искажены и не могут быть обобщены на всю популяцию студентов.

Систематические ошибки

Систематические ошибки возникают, когда существует постоянное искажение в сборе или обработке данных. Например, если при проведении опроса используется неправильный метод измерения или если данные собираются только из определенной группы людей, это может привести к систематической ошибке и искажению результатов.

Случайные ошибки

Случайные ошибки возникают из-за случайных факторов, которые могут влиять на результаты. Например, при измерении физической величины могут возникнуть случайные ошибки из-за неточности приборов или неправильного измерения. Эти ошибки могут быть минимизированы путем повторных измерений и усреднения результатов.

Искажение выборки

Искажение выборки возникает, когда некоторые группы или категории в выборке представлены неравномерно или недостаточно. Например, если при проведении опроса большинство респондентов являются молодыми людьми, это может привести к искажению результатов и невозможности обобщения на всю популяцию.

Искажение ответов

Искажение ответов возникает, когда респонденты предоставляют неправдивую или неполную информацию. Это может быть вызвано различными факторами, такими как социальное желание быть положительно оцененным или страх перед негативными последствиями. Искажение ответов может привести к неправильным выводам и искажению результатов исследования.

Важно учитывать эти ошибки и искажения при работе с данными и применении статистических методов. Это поможет получить более точные и надежные результаты и избежать неправильных выводов

Что такое точечный график?

Мы можем представить корреляцию между количественными переменными в графической сводке, используя график, называемый точечной диаграммой.

Точечный график выглядит следующим образом:

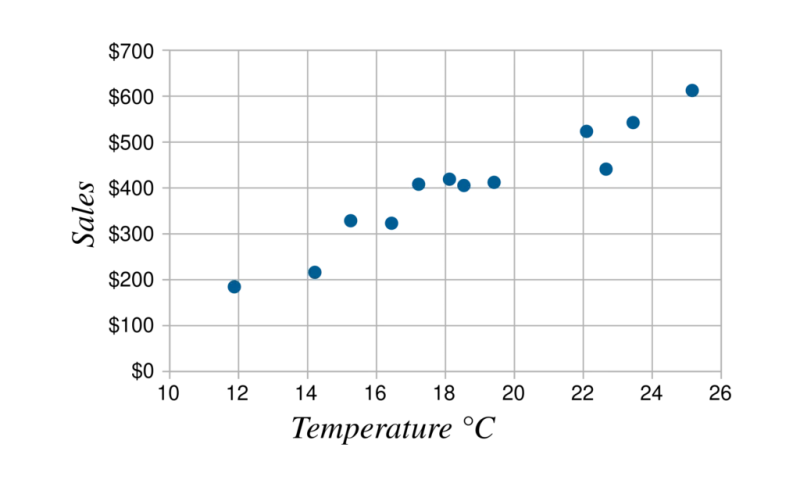Точечные (XY) графики (mathsisfun.com )

Подробнее о точечных графиках вы можете прочитать здесь.

Заключение и изучение большего

В этом руководстве мы изучили некоторые фундаментальные концепции статистики, которые помогут вам более эффективно работать с вашими данными.

Но обучение на этом не заканчивается – есть несколько фундаментальных тем, с которыми вы должны быть знакомы. Поскольку это только начало, вы можете углубиться, обратившись к онлайн-ресурсам или учебникам.

Что такое Boxplot?

Еще одной отличной визуализацией, которая поможет вам визуализировать распределение ваших данных, является boxplot.

Блок-схема, например, позволяет вам визуально наблюдать, есть ли какие-либо отклонения в вашей коллекции данных. Он включает такие термины, как минимум, 25-й процентиль, 50-й процентиль, 75-й процентиль и максимум. Коробочный график выглядит следующим образом:

Изображение Ибрагима Огунбийи

Итак, давайте рассмотрим то, что мы имеем на приведенной выше диаграмме:

Минимум: Минимальное значение не подразумевает наименьшее значение в нашем наборе данных. Он рассчитывается по этой формуле ( Q1 -1,5*IQR), где:

• Q1 – подразумевает 25 — й процентиль
• IQR – подразумевает межквартильный диапазон (который представляет собой разницу между 75-м процентилем и 25-м процентилем).

При минимальном значении это может помочь нам обнаружить точки данных, которые также намного ниже других наблюдаемых значений.

Например, предполагая, что наши точки данных распределены следующим образом . Мы можем видеть, что значение 10 также является выбросом, потому что это меньшее значение, которое намного ниже других наблюдений.

25-й процентиль — это значение, которое говорит нам, что 25% наших точек данных ниже этого значения и 75% наших точек данных выше этого значения. 25-й процентиль также известен как первый квартиль.

50-й процентиль — это значение, которое указывает, что 50% наших точек данных ниже этого значения, а остальные 50% выше этого значения. Он также известен как второй квартиль.

75-й процентиль — это значение, которое говорит нам, что 75 процентов наших данных находятся ниже этого значения, а оставшиеся 25 процентов — выше него. Он также известен как третий квартиль.

Максимум: Также, как и минимум, максимум не подразумевает наибольшее значение в наборе данных. Он рассчитывается по формуле (Q3 + 1,5*IQR), где:

• Q3 – подразумевает 75 — й процентиль
• IQR подразумевает межквартильный диапазон (который представляет собой разницу между 75-м процентилем и 25-м процентилем).

С помощью maximum также это может помочь нам обнаружить точки данных, которые также намного превышают другие наблюдаемые значения.

Например, предполагая, что наши точки данных распределены следующим образом . Мы можем видеть, что значение 645 также является выбросом, потому что это более высокое значение, которое намного превосходит другие наблюдения.

Мы видели несколько графических сводок того, с чем нам придется иметь дело ежедневно. Давайте посмотрим на заключительную тему, которую мы обсудим в этой статье: