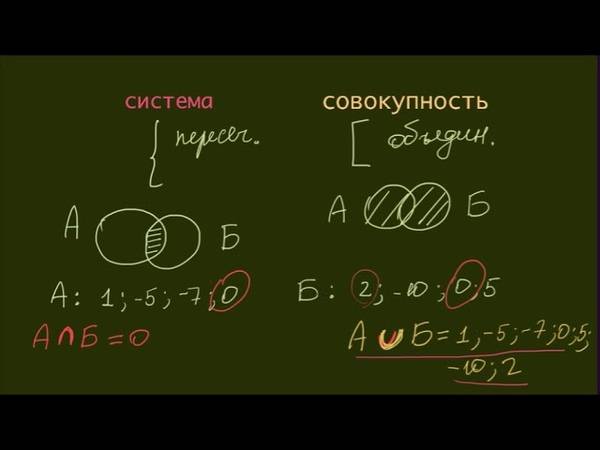Чем система отличается от совокупности в математике

Отличие системы от совокупности

Совокупность в математике представляет собой набор отдельных объектов или элементов, которые могут быть какими угодно. Они могут иметь различные характеристики и не обязательно связаны между собой никакими отношениями или правилами. Примером совокупности может служить множество натуральных чисел от 1 до 10.

В отличие от этого, система в математике представляет собой набор элементов, которые связаны между собой определенными отношениями или правилами. Эти отношения и правила определяют внутреннюю структуру системы и определяют, как элементы взаимодействуют друг с другом. Примером системы может служить множество натуральных чисел вместе с операциями сложения и умножения, которые определены для этих чисел.

Совокупность может быть неупорядоченной и не иметь специальной структуры или связей между элементами. В отличие от этого, система обладает внутренней организацией и может быть упорядоченной или иметь определенную структуру.

Кроме того, система может иметь свойства эмерджентности, когда она представляет собой целое, которое больше суммы его частей. Появление новых свойств или характеристик внутри системы происходит благодаря взаимодействию ее элементов и правилам, которые ее определяют. Совокупность не обладает подобными свойствами эмерджентности.

Таким образом, основное отличие системы от совокупности в математике заключается в том, что система представляет собой организованное и упорядоченное целое, где элементы связаны между собой определенными отношениями или правилами, в то время как совокупность — это неупорядоченный набор элементов без внутренней структуры или связей.

В чем разница

Несмотря на сходства, присутствуют и различия. И главное в том, что совокупность в узком, точном смысле никогда не имеет упорядоченности, а система – имеет всегда. Например, песчинки в пустыне, если рассматривать их сами по себе, представляют собой совокупность. Но сама пустыня – это система, в которой песок – один из элементов и находится во взаимосвязи со всеми остальными элементами.

Система может состоять из разнородных объектов. И единственным, что иногда объединяет по смыслу ее элименты, может быть факт того, что это все части одной системы. Примером этого служит системный блок персонального компьютера.

Если не брать в расчет, что все это комплектующие ПК, результат наукоемких отраслей электроники, выполнены часто из схожих материалов, а сравнить их исключительно по функционалу, получится: Каждый элемент выполняет свою специфическую задачу и принцип его работы (в большинстве случаев) принципиально отличается от других. Пример, конечно, не идеален. Ведь все компоненты компьютера работают за счет потока электронов. Но в природе почти нет идеальных примеров, только относительные. По крайней мере, ясна суть.

Есть еще одно различие между совокупностью и системой. Если совокупность существует в узком смысле и широком, соответственно как неупорядоченное скопление и любое скопление, то с термином «система» такого нет. Это всегда в первую очередь упорядоченное скопление, иными словами – модель.

Если подытожить, разница между совокупностью и системой такова:

Система всегда упорядочена, совокупность – не всегда.
Система может состоять из ничем не схожих объектов.
Понятие «система» более конкретное и узкое.

В математике: чтобы решить совокупность, требуется объединить результаты каждого решения. Чтобы решить систему, требуется произвести пересечение результатов решений. Иногда удобнее одно, иногда другое. Но при работе с большими данными, пожалуй, лучше подойдет система. Быстрее и эффективнее.

В заключение, стоит отметить, что совокупность и система во многом схожи. Но и отличия принципиальные. Вот почему это два качественно разных понятия и явления. И если их путать, это приведет к неверным выводам и в математике, и в философии, и в бытовых вопросах.

Различия между системой и совокупностью

Первое отличие между системой и совокупностью заключается в их структуре и связях. Система представляет собой единство компонентов, взаимодействующих между собой. У системы есть определенные функции и цели, которые она выполняет благодаря установленным взаимосвязям и взаимодействию ее элементов. В то время как совокупность — это просто совокупность отдельных элементов или объектов, не имеющих между собой организационной структуры.

Второе отличие заключается в функциях, которые выполняют система и совокупность. Система имеет свои функции, которые специфичны и определяются ее целями и спецификой компонентов. Функции системы направлены на достижение определенных результатов и решение заданных задач. В то время как совокупность не имеет своих функций, она представляет собой лишь совмещение различных объектов, без единой организации и направления.

Третье отличие связано с организацией и структурой. Система характеризуется своими компонентами, их взаимосвязью и единством. Компоненты системы взаимодействуют друг с другом в определенном порядке и определенные функции выполняются благодаря этой организации. В то время как совокупность не имеет организованной структуры и взаимосвязи между ее элементами.

Четвертое отличие заключается в концепции комплекса. Система представляет собой комплексное образование, где каждый компонент несет свою роль в достижении общей глобальной цели. В случае с совокупностью, элементы могут быть независимыми и не связанными между собой. Они не образуют единого комплекса и могут существовать самостоятельно.

В итоге, система и совокупность — это разные концепции, которые характеризуют объекты и явления по-разному. Система имеет структуру, связь, взаимодействие и компоненты, выполняющие определенные функции в рамках организации. Совокупность же представляет собой просто совокупность отдельных объектов или элементов, без единой структуры и связей между ними.

Основные отличия в структуре

Компоненты системы связаны между собой определенными отношениями, обеспечивая ее функционирование. В отличие от системы, совокупность представляет собой простое объединение отдельных элементов без необходимой организации и взаимосвязи.

Структура системы имеет важное значение, поскольку определяет ее способность выполнять свои функции. В системе все компоненты взаимосвязаны и взаимодействуют друг с другом, обеспечивая ее работу в целом. Совокупность же представляет собой простое собрание элементов, не связанных между собой

Каждый элемент совокупности функционирует независимо и не влияет на другие элементы

Совокупность же представляет собой простое собрание элементов, не связанных между собой. Каждый элемент совокупности функционирует независимо и не влияет на другие элементы.

Различия взаимодействия элементов

Система представляет собой организованную структуру, где элементы взаимосвязаны и взаимодействуют друг с другом в целях достижения определенной цели. Эти элементы образуют единый комплекс, функционируя во взаимодействии и взаимозависимости друг от друга. Отличительной особенностью системы является то, что изменение или удаление одного из элементов может повлиять на функционирование всего комплекса.

Совокупность, в свою очередь, представляет собой простую сумму элементов, которые могут находиться во взаимодействии друг с другом, но не образуют единой структуры или комплекса. Они существуют независимо друг от друга и функционируют индивидуально, выполняя свои специфические функции.

Таким образом, основное различие между системой и совокупностью заключается в их организации и взаимодействии элементов. В системе элементы образуют единую структуру, где каждый компонент выполняет свою функцию в рамках общей цели, в то время как в совокупности элементы существуют независимо и не образуют организованной структуры.

Практическое применение совокупностей и систем

Совокупности в математике используются для описания групп и собирательных понятий. Они полезны, когда требуется объединить множество объектов или факторов в одно целое. Например, совокупность людей в определенном регионе может быть использована для анализа статистики населения или для изучения взаимосвязей между различными социальными группами.

Системы, с другой стороны, описывают взаимодействие и внутренние связи между различными компонентами. Они помогают понять сложные процессы и функционирование объектов в реальном мире. Например, система транспортного движения может включать в себя дороги, автомобили, пешеходы, светофоры и другие элементы, которые взаимодействуют между собой и образуют сложную систему передвижения.

Практическое применение совокупностей и систем включает в себя множество областей, таких как экономика, социология, биология, информатика и технические науки. Они помогают ученым и специалистам анализировать и предсказывать сложные явления, принимать решения и улучшать существующие системы.

Например, совокупности и системы используются для анализа экономических данных и прогнозирования поведения рынка. Они помогают ученым изучать социальные тенденции, взаимодействие между группами людей и предсказывать результаты социальных экспериментов. В биологии совокупности и системы используются для изучения популяций и экосистем, а также для анализа особей и генетических взаимосвязей.

В информатике и технических науках совокупности и системы используются для проектирования и управления сложными системами, такими как компьютерные сети, производственные процессы, автоматические системы и другие. Они помогают улучшить эффективность и надежность систем, предотвращать сбои и оптимизировать работу.

В целом, практическое применение совокупностей и систем играет важную роль в различных областях знания. Они позволяют анализировать сложные явления, делать прогнозы и улучшать существующие системы.

Что такое совокупность?

Совокупность — это группа или набор элементов или объектов, которые объединены общим признаком или свойством. Упорядоченная и неупорядоченная совокупность может содержать различные типы данных, включая числа, строки, булевы значения и другие.

Совокупность может быть представлена в виде списка или таблицы. В списках элементы могут быть упорядочены или неупорядочены, а в таблицах элементы могут быть организованы в ячейки и столбцы.

Одним из ключевых свойств совокупности является то, что элементы в ней могут повторяться. Например, в совокупности чисел {1, 2, 2, 3, 4} число «2» встречается дважды. Это отличает совокупность от множества, в котором повторяющиеся элементы не допускаются.

Совокупность может быть использована для представления различных данных, например, список товаров в магазине, данные о клиентах, результаты опросов и т. д. Элементы совокупности могут быть обработаны с использованием различных алгоритмов и операций, таких как поиск, сортировка, фильтрация и другие.

Применение в разных областях

Термины «система» и «совокупность» находят широкое применение в различных областях человеческой деятельности. Оба понятия имеют свои особенности и контексты использования, которые определяются уникальными требованиями и целями каждой области.

В инженерии и технических науках, например, использование термина «система» обычно относится к совокупности взаимосвязанных элементов, которые работают вместе для достижения определенной функции или цели. Это может быть электрическая система, механическая система или программная система. В таком случае «система» имеет четкую структуру и заданные правила взаимодействия между ее компонентами.

В гуманитарных науках, понятие «совокупность» обычно используется для описания набора объектов, явлений или событий, которые связаны общей характеристикой или категорией, но без четкой структуры или организации. Например, совокупность фактов, совокупность идей или совокупность людей.

В экономике и управлении также используются оба термина в разных контекстах. «Система» может относиться к организационной структуре, процессам или подходам, используемым в предприятии или организации для достижения определенных целей. «Совокупность» же может применяться для обозначения суммы всех элементов или переменных, связанных с определенным аспектом экономики или рынка.

В области социальных наук и искусств также используются оба термина, чтобы описать различные структуры, явления или процессы. «Система» может относиться, например, к социальной системе или системе значений, которые влияют на поведение и взаимодействие людей. С другой стороны, «совокупность» может использоваться для обозначения набора элементов, связанных с определенным направлением или формой искусства.

Таким образом, понятия «система» и «совокупность» находят широкое применение в самых разных областях человеческой деятельности, где они используются для описания различных взаимосвязей и структур

Важно различать и учитывать контексты использования каждого термина, чтобы точно передать свои идеи и концепции в соответствующей области

Правила записи решений строгих и нестрогих неравенств

До сих пор мы говорили о неравенствах как о способе записи результата сравнения двух чисел: 2 > 1 или 3,5 < 7. Но неравенства можно использовать и для записи различной информации об ограничениях для того или иного объекта. В жизни мы часто используем такие ограничения для описания, например: Россия – это миллионы людей от Калининграда до Владивостока; в лифте можно перевозить не больше 1000 кг, а в пакет – класть не больше 20 кг. Ограничения могут быть использованы и для классификации объектов. Например, в зависимости от возраста выделяют различные категории населения – дети, подростки, молодёжь и т.д.

Во всех рассмотренных примерах можно выделить общую идею: некоторая величина ограничена сверху или снизу (или с обеих сторон сразу). Если M – грузоподъёмность лифта, а – допустимая масса товаров, которые можно класть в пакет, то описанную выше информацию можно записать так: M < 1000, m < 20 и т.д.

В рассмотренных примерах мы были немного неточны. Формулировка «не больше» подразумевает, что в лифте можно перевозить ровно 1000 кг, а в пакет можно положить ровно кг. Поэтому правильнее было записать так: M = 1000 или M < 1000. Естественно, так писать неудобно, поэтому придумали специальный знак: , который читается как «меньше или равно». Такие неравенства называются нестрогими (соответственно, неравенства со знаками <, > – строгими). Их используют тогда, когда переменная может быть не только строго больше или меньше, но может и равняться граничному значению.

Решением неравенства называются все такие значения переменной, при подстановке которых полученное числовое неравенство будет верным. Рассмотрим, например, неравенство:. Числа 6;8;5,5 – решения этого неравенства, т.к. неравенства 6 > 5; 8 > 5; 5,5 > 5 являются верными. А вот числа 4 и 5 не являются решениями, поскольку числовые неравенства 4 > 5 и 5 > 5 не являются верными. Решить неравенство, значит, найти все значения переменных, при которых неравенство будет верным.

Вернемся к неравенству. Его решения можно эквивалентно описать так: все действительные числа, которые больше 5. Понятно, что таких чисел бесконечное множество, как же в таком случае записать ответ? Обратимся к числовой оси: все числа, большие 5, расположены справа от 5. Заштрихуем эту область, тем самым показывая, что это и будет ответ к нашему неравенству. Чтобы показать, что число 5 не является решением, его заключают в пустой круг, или, по-другому, выкалывают точку (Рис. 7).

Рис. 7. На числовой оси показано, что число 5 не является решением (выколотая точка)

Если же неравенство нестрогое и выбранная точка является решением, то её заключают в закрашенный круг.

Рис. 8. На числовой оси показано, что число 5 является решением (закрашенная точка)

Итоговый ответ удобно записывать с помощью промежутков. Промежуток записывается по следующим правилам:

Записываются левая и правая границы промежутка.
Если граница включена в промежуток, т.е. неравенство нестрогое, ставят квадратные скобки []; если неравенство строгое и граница не включена, то скобки круглые ().
Если у промежутка нет правой границы, то её записывают как или , если нет левой границы, то как .

Знак обозначает бесконечность, т.е. показывает, что число может принимать сколь угодно

большое () или сколь угодно малое значение ().

Ответ к неравенству мы можем записать так:

или просто:

Это означает, что неизвестная принадлежит указанному промежутку, т.е. может принимать любые значения из этого промежутка.

Если обе скобки промежутка круглые, как в нашем примере, то такой промежуток ещё называют интервалом.

Слайд 15Замечание.В случае, если вы не уверены в том, что правильно

используете знак «система», «совокупность», то лучше этого избежать. На экзамене

за неверное использование математической символики может быть снижен балл. Однако, в литературе и в различных ресурсах интернета эта символика используется очень часто. Например, при решении неравенств с модулями с использованием альтернативных переходов. Поэтому полезно все – же ориентироваться в данных понятиях.

Как можно записать начало решения, например, иррационального уравнения (экзамен)?

ОДЗ:

Условие существования корней:

Возведем обе части в квадрат:

Условно. (на самом деле даже при выполнении этого условия корней может не быть)

Все записи верны.

Неравенства с модулем

Разобравшись, как решаются уравнения с модулем, можно приступать к неравенствам.

Пример 5. Решите неравенство x2 — |3x — 7| + 7 >= 0.

Решение. Найдем, при каких значениях х модуль равен 0. Получаем 3x = 7 \(\rightarrow\) \(x = \frac{7}{3}\).

Определим, с какими знаками модуль будет раскрываться на каждом промежутке.

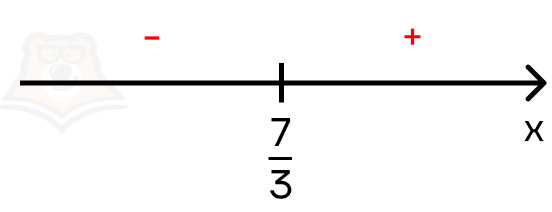
Осталось рассмотреть неравенство на двух промежутках.

1. \(x \leq \frac{7}{3}\), тогдаx2 — (-(3x — 7)) + 7 >= 0x2 + 3x — 7 + 7 >= 0x2 + 3x >= 0x(x + 3) >= 0

Решим это неравенство «Методом интервалов». Сразу учтем ограничение \(x \leq \frac{7}{3}\).

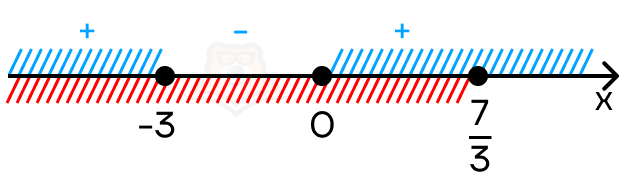
Получаем, что решением неравенства на заданном промежутке будет \(x \in (-\infty; -3] U\).

2. \(x > \frac{7}{3}\), тогда x2 — 3x + 7 + 7 >= 0x2 — 3x + 14 >= 0x2 — 3x + 14 = 0D = 9 — 56 = -47 — корней на заданном отрезке не будет.

Может ли решением квадратного неравенства быть любое число, если дискриминант меньше 0? Вспомним, что корни квадратного уравнения — это точки пересечения параболы и оси х. Если парабола не пересекает ось х, то неизбежно лежит выше или ниже ее. Поскольку в нашем случае ветви параболы направлены вверх, мы можем нарисовать ее примерный график. Так как парабола задается функцией y = x2 — 3x + 14, то неравенство будет выполняться при всех y >= 0. Парабола целиком попадает в эту область, а решением неравенства будет любое х.

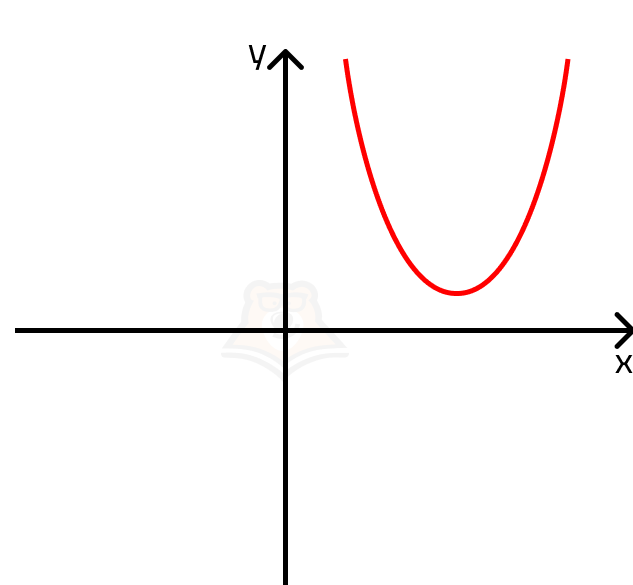
Однако не стоит забывать про ограничение \(x > \frac{7}{3}\). Накладывая его, получаем решение \((\frac{7}{3}; + \infty)\).

Осталось только объединить полученные на промежутках решения:

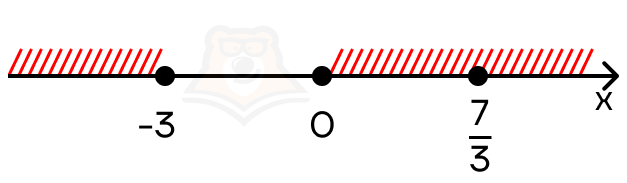
Получаем, что \(x \in (-\infty;- 3] U [0; +\infty)\).

Ответ: \(x \in (-\infty;- 3] U [0; +\infty)\)

Рассмотрим неравенства вида |f(x)| > a и |f(x)| < a, где а — некоторое число и a >= 0. Модуль можно раскрыть двумя способами и получить два неравенства. Но будет это совокупность или система?

Это зависит от знака. Разберем случай |f(x)| > a. Заметим, что строгость знака может быть любой. Тогда модуль раскрывается как:

f(x) > a и -f(x) > a \(\rightarrow\) f(x) < -a.

Отметим эти промежутки на числовой прямой:

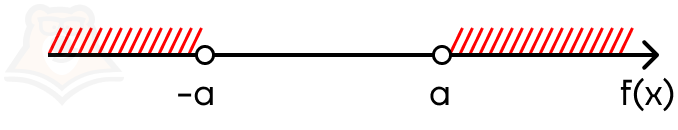
В ответе должны оказаться оба промежутка — их нужно объединить. В этом случае модуль раскрывается в совокупности.

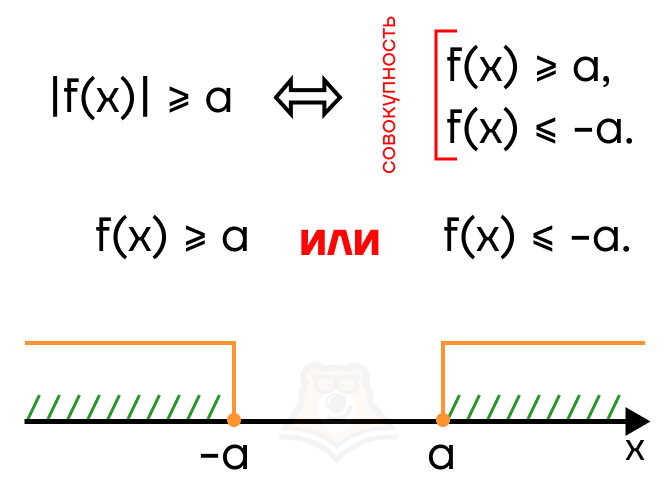
Рассмотрим случай |f(x)| < a, здесь строгость знака также может быть любой. Раскроем модуль: f(x) < 0 и -f(x) < a \(\rightarrow\) f(x) > -a. На числовой прямой это будет выглядеть следующим образом:

В в ответе должен оказаться промежуток от —а до а. Следовательно, необходимо воспользоваться системой, чтобы “отсечь” лишние промежутки.

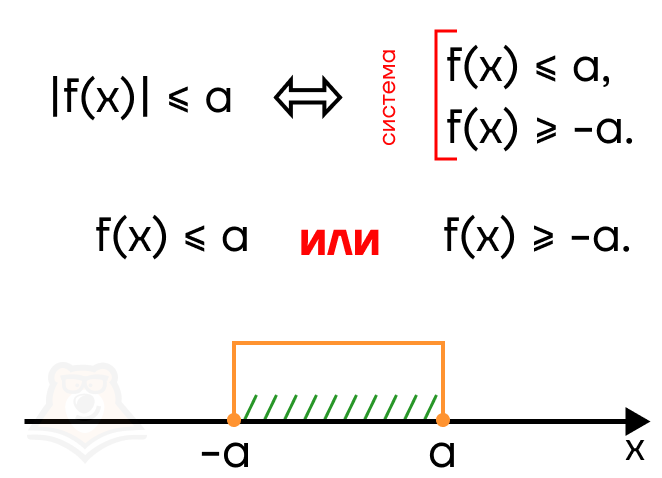
Можно ли обойтись в этом случае без раскрытия модуля? Да, но необходимо возвести неравенство в квадрат.

|f(x)| ⋁ a | \(\uparrow\) 2 — вместо ⋁ может стоять любой знак неравенства. f2(x) ⋁ a2f2(x) — a2 ⋁ 0

Воспользуемся формулой сокращенного умножения:

(f(x) — a)(f(x) + a) ⋁ 0

Однако стоит помнить, что обе части неравенства можно возвести в квадрат только в том случае, если они неотрицательны. То есть обязательно должно выполняться условие a0.

Мы получили равносильный переход. Но существуют ли равносильные переходы, если вместо числа а стоит другая функция или даже модуль? Да. Они выводятся таким же способом, как и переход для неравенства с числом. Получаем еще два равносильных перехода:

|f(x)| ⋁ g(x) \(\rightarrow\) (f(x) — g(x))(f(x) + g(x)) ⋁ 0

g(x) обязательно должно быть неотрицательным, чтобы можно было возвести неравенства в квадрат.

|f(x)| ⋁ |g(x)| \(\rightarrow\) (f(x) — g(x))(f(x) + g(x)) ⋁ 0

Разберем на примере, как можно использовать равносильный переход. Для этого возьмем то же неравенство, что и в примере 5, но решим его по-другому.

Пример 6. Решите неравенство x2 — |3x — 7| + 7 >= 0.

Решение. Перенесем модуль в другую часть неравенства:

|3x — 7| <= x2 + 7. Модуль всегда неотрицателен. Правая часть неравенства неотрицательна, поскольку число в квадрате всегда положительно.

Повторим действия, чтобы прийти к равносильному переходу:

(3x — 7)2 <= (x2+7)2(3x-7)2 — (x2 + 7)2 <= 0(3x — 7 — (x2 + 7))(3x — 7 + x2 + 7) <= 0(3x — 7 — x2 — 7)(3x + x2) <= 0(-x2 + 3x — 14) * x(3 + x) <= 0-(x2 — 3x + 14) * x(3 + x) <= 0(x2 — 3x + 14) * x(3 + x) <= 0

Рассмотрим первую скобку:

x2 — 3x + 14 = 0

D = 9 — 56 = -47 — корней нет. Выражение всегда будет положительно, то есть на него можно разделить все неравенство. Получаем:

x(3 + x) <= 0

Тогда \(x \in (-\infty;- 3] U [0; +\infty)\)

Ответ: \(x \in (-\infty;- 3] U [0; +\infty)\)

При решении можно сразу использовать равносильный переход, не расписывая его.

Итак, неравенства с модулем можно решить двумя способами: раскрывать модуль и воспользоваться равносильным переходом. Выбор способа зависит от личных предпочтений и удобства решения.

Презентация на тему: ” Системы и совокупности. МБОУ г. Мурманска гимназия 3 Шахова Татьяна Александровна.” — Транскрипт:

Системы и совокупности. МБОУ г. Мурманска гимназия 3 Шахова Татьяна Александровна

1) Понятия: система, совокупность. Содержание. 2) Алгоритмы решения систем и совокупностей уравнений и неравенств с одной переменной. 3) Тренировочные упражнения с пошаговым разбором. В ресурсе сделан акцент на использование понятий система – совокупность и правильное применение математической символики на примерах систем (совокупностей), содержащих квадратные уравнения и рациональные неравенства, подробное решение которых не предоставлено. При необходимости повтори: -решение квадратных уравнений: -решение линейных неравенств: -решение рациональных неравенств:

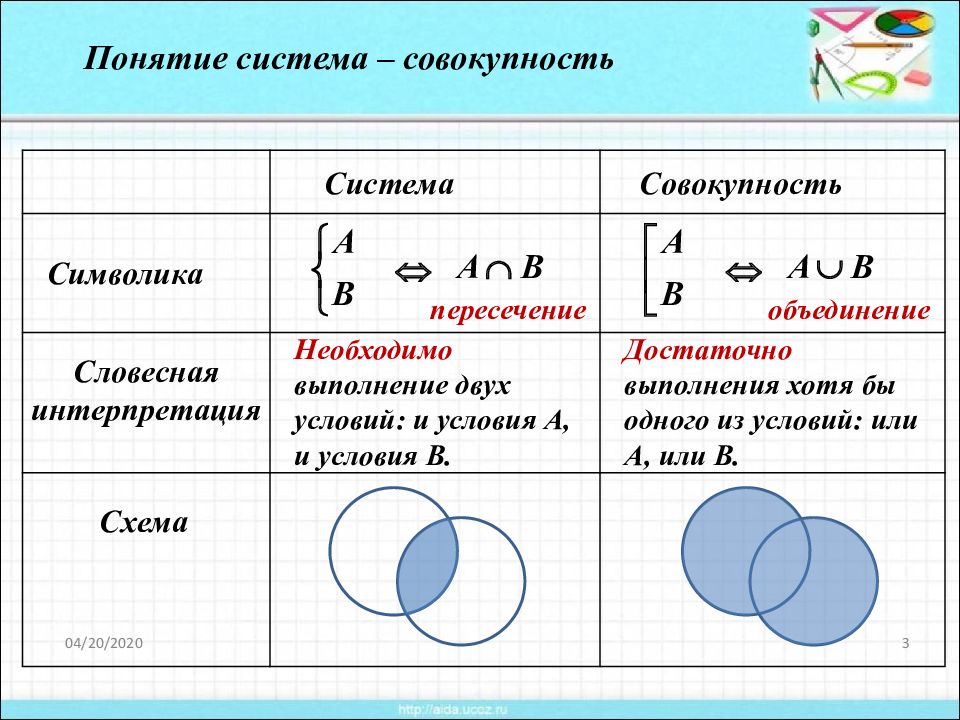
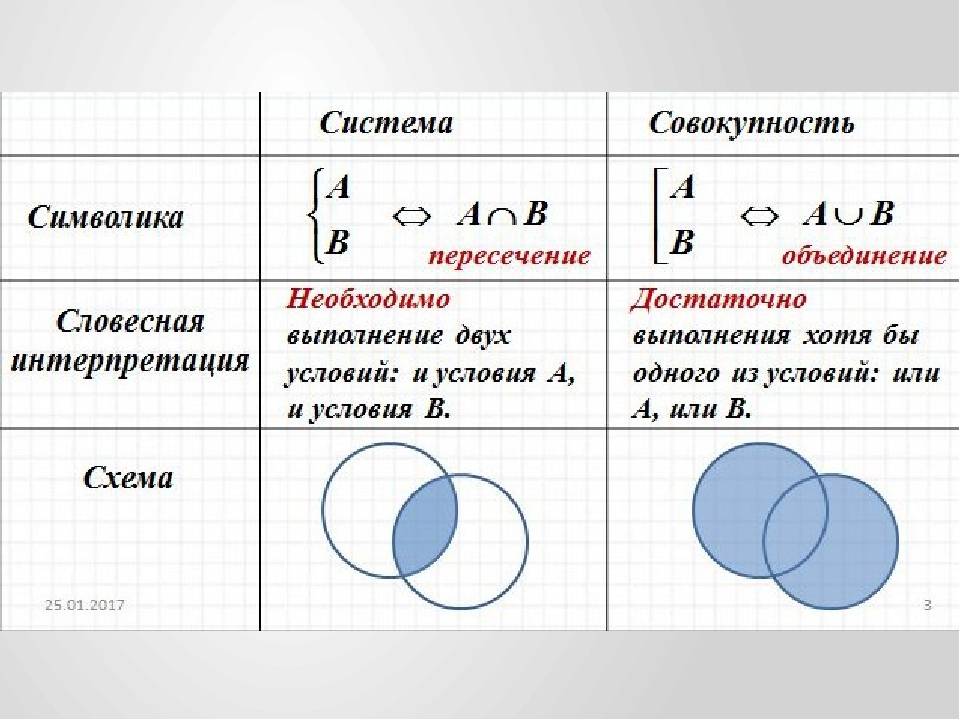
Понятие система – совокупность Система Совокупность Символика Словесная интерпретация Схема Необходимо выполнение двух условий: и условия А, и условия В. Достаточно выполнения хотя бы одного из условий: или А, или В. пересечение объединение

Понятие система – совокупность присутствует в решении квадратного уравнения по теореме Виета Необходимо выполнение двух условий: и первого, и второго – система. Для обращения уравнения в верное равенство достаточно выполнения хотя бы одного из условий: или первого, или второго – совокупность.

Система Совокупность Решение системы уравнений с одной переменной. Решение совокупности уравнений с одной переменной. 1) Решить каждое уравнение независимо одно от другого. 2) В ответ записать общие решения данных уравнений. 1) Решить каждое уравнение независимо одно от другого. 2) В ответ записать все решения данных уравнений.

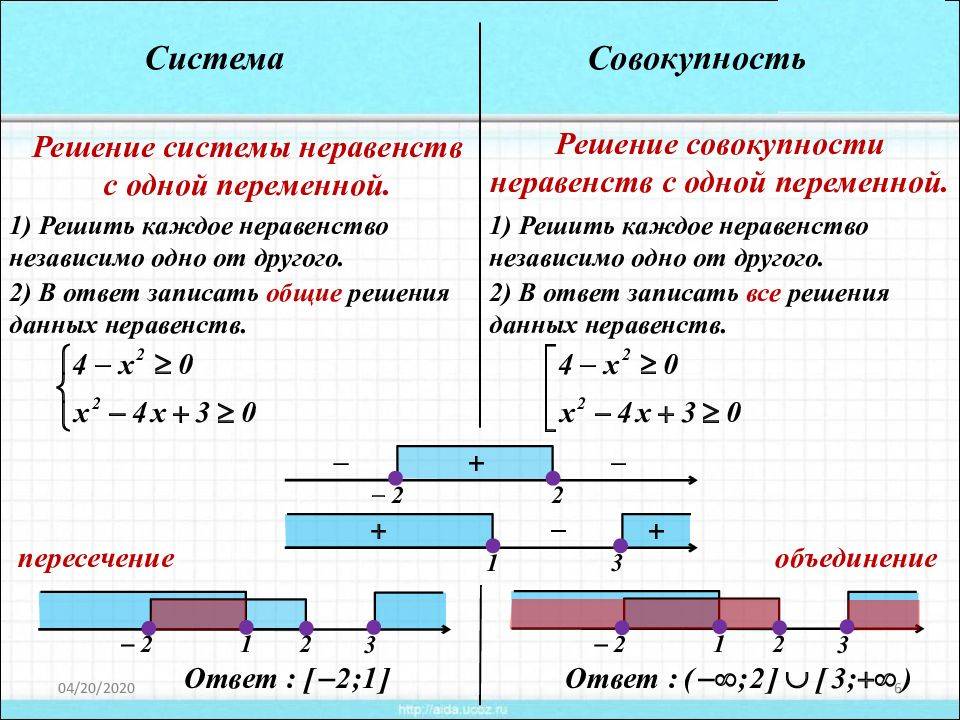
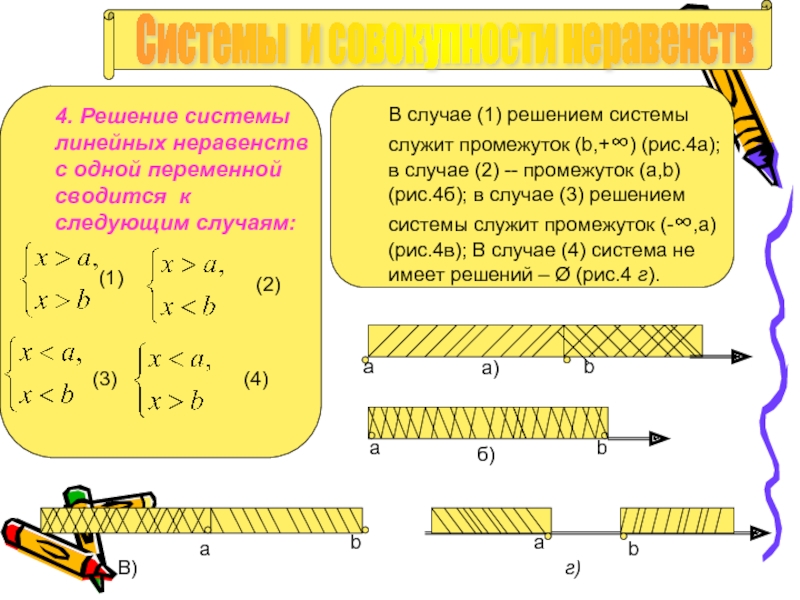
Система Совокупность Решение системы неравенств с одной переменной. Решение совокупности неравенств с одной переменной. 1) Решить каждое неравенство независимо одно от другого. 2) В ответ записать общие решения данных неравенств. 1) Решить каждое неравенство независимо одно от другого. 2) В ответ записать все решения данных неравенств. пересечение объединение

Решите уравнение: Некоторые задачи, при решении которых возникает понятие система – совокупность. Так как квадрат принимает только неотрицательные значения, то рассматриваемая сумма может быть равна нулю только в случае, если и то и другое слагаемое принимают значение ноль (система).

Решите уравнение: Некоторые задачи, при решении которых возникает понятие система – совокупность. Произведение равно нулю, если хотя бы один множитель равен нулю, или первый, или второй (совокупность).

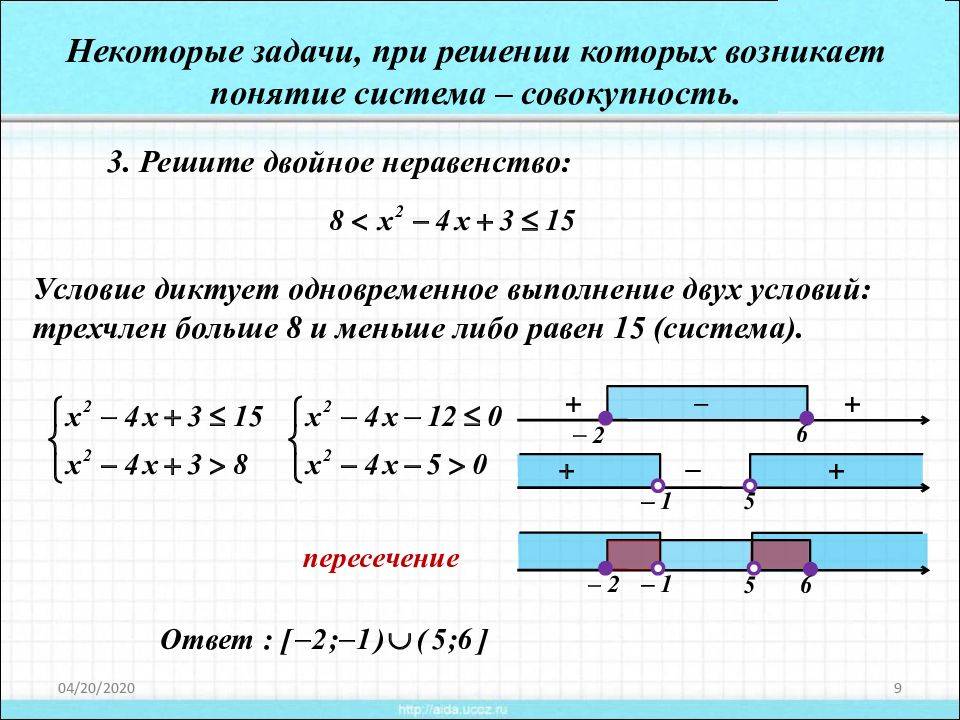
Решите двойное неравенство: Некоторые задачи, при решении которых возникает понятие система – совокупность. Условие диктует одновременное выполнение двух условий: трехчлен больше 8 и меньше либо равен 15 (система). пересечение

Решите неравенство методом замены переменной: Некоторые задачи, при решении которых возникает понятие система – совокупность. – совокупность. объединение

Решите неравенство методом замены переменной: Некоторые задачи, при решении которых возникает понятие система – совокупность. – система Ø пересечение

Найдите область определения функции. Некоторые задачи, при решении которых возникает понятие система – совокупность. пересечение Условие существования квадратного корня: Условие существования дроби:

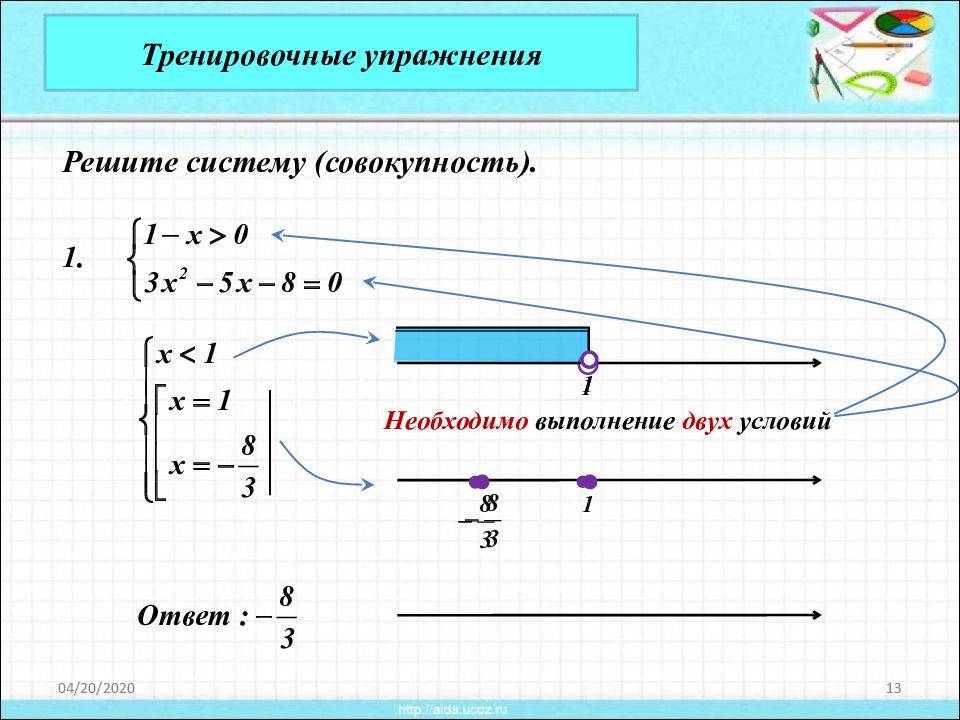
Тренировочные упражнения Решите систему (совокупность). Необходимо выполнение двух условий

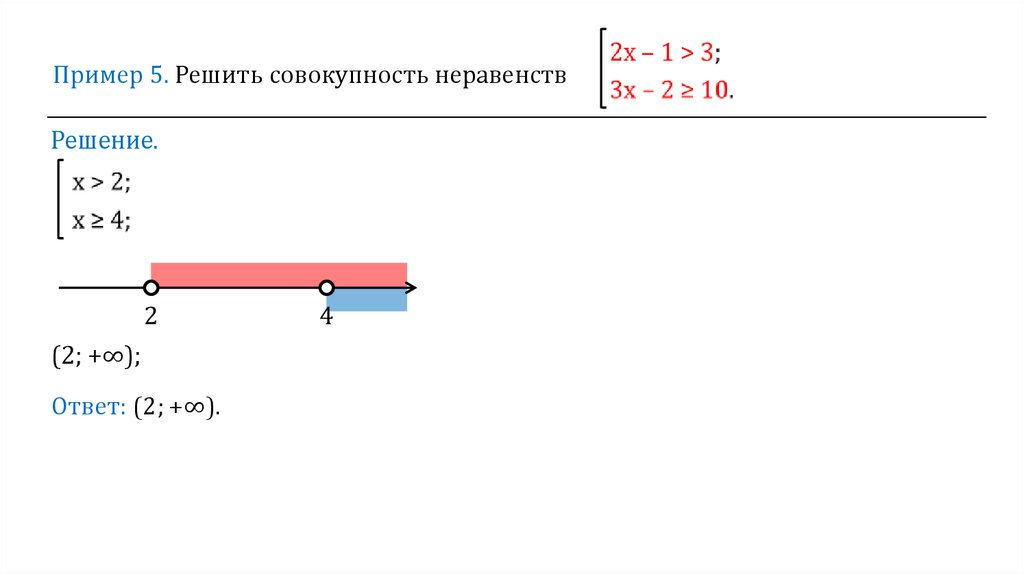
Тренировочные упражнения Решите систему (совокупность). Достаточно выполнения хотя бы одного из двух условий

Замечание. В случае, если вы не уверены в том, что правильно используете знак «система», «совокупность», то лучше этого избежать. На экзамене за неверное использование математической символики может быть снижен балл. Однако, в литературе и в различных ресурсах интернета эта символика используется очень часто. Например, при решении неравенств с модулями с использованием альтернативных переходов. Поэтому полезно все – же ориентироваться в данных понятиях. Как можно записать начало решения, например, иррационального уравнения (экзамен)? ОДЗ: Условие существования корней: Возведем обе части в квадрат: Условно. (на самом деле даже при выполнении этого условия корней может не быть) Все записи верны.

Спасибо за внимание. В следующих ресурсах рассмотренные понятия и символы будут использоваться