Разница между волной и колебаниями

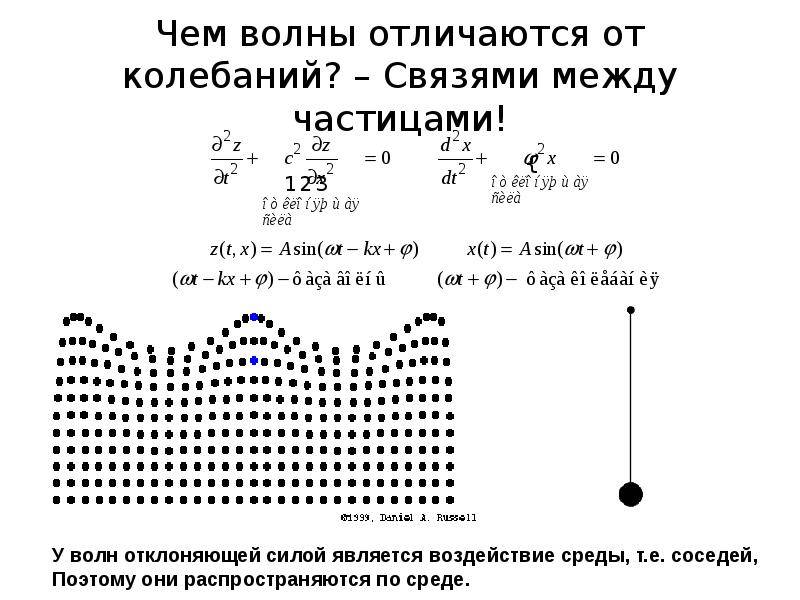
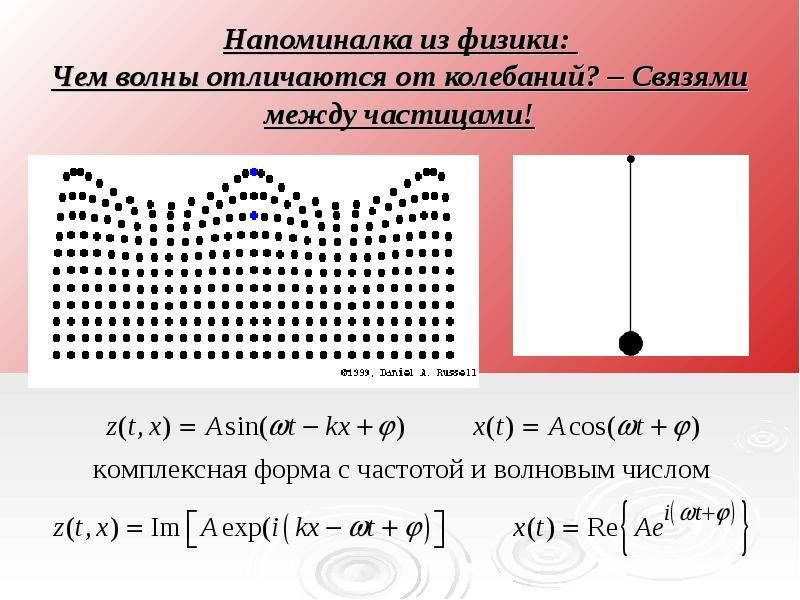
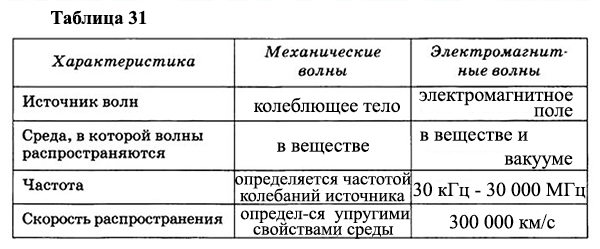
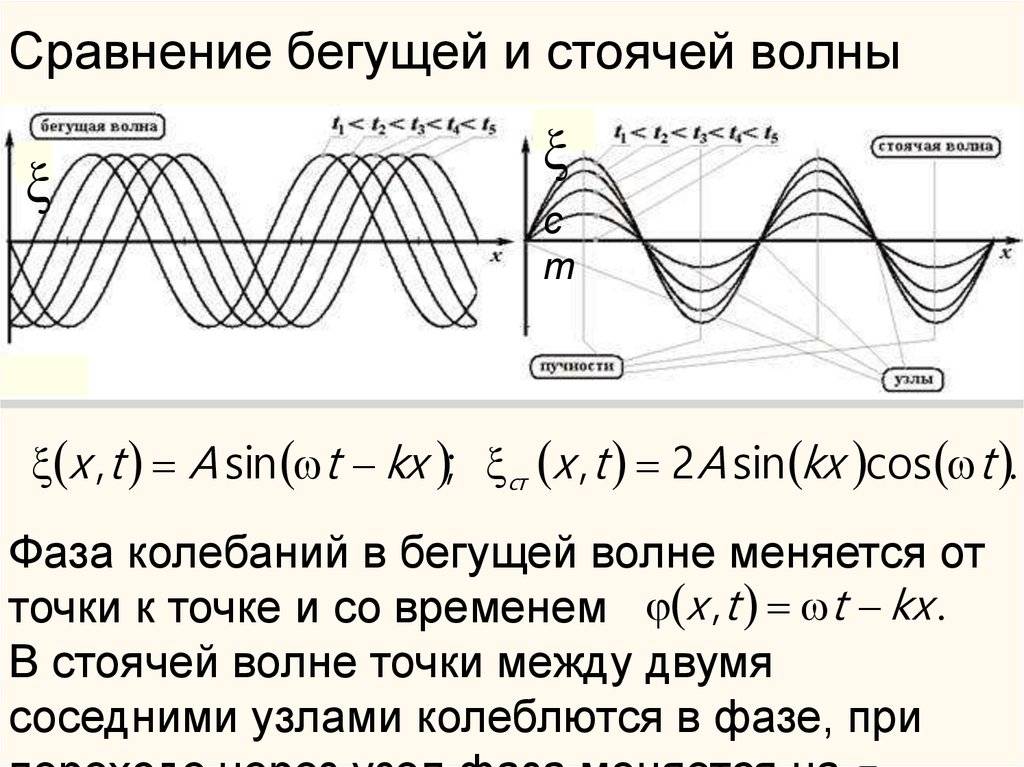
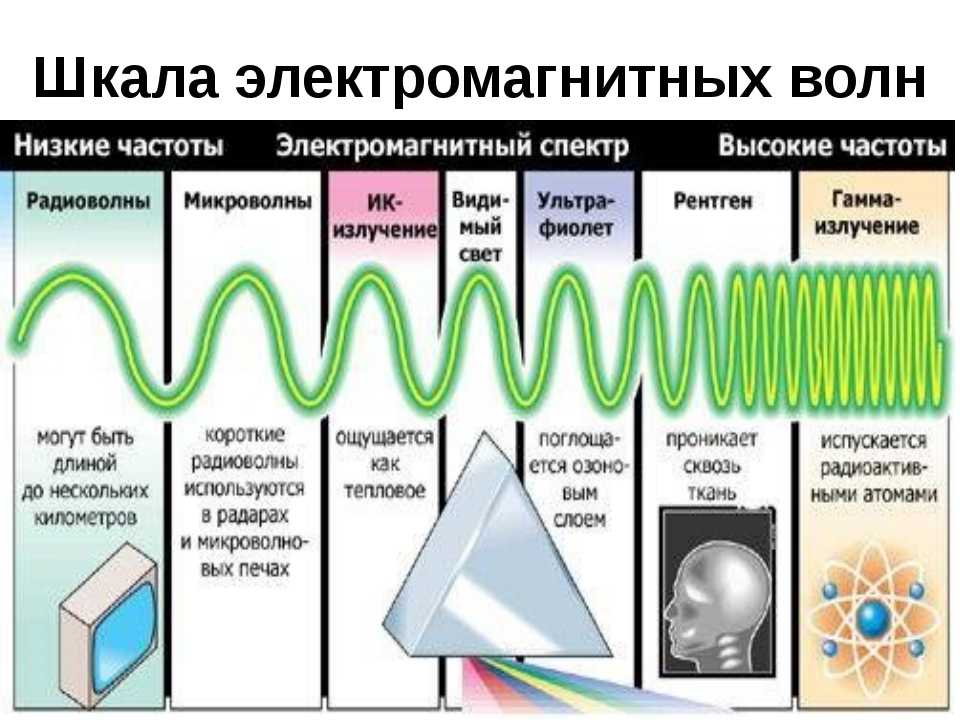
Электромагнитные волны

1. Электромагнитными волнами называются возмущения электромагнитного поля (т.е. переменное электромагнитное поле), распространяющиеся в пространстве.

Утверждение о существовании электромагнитных волн является непосредственным следствием решения системы уравнений Максвелла. Согласно этой теории следует, что переменное электромагнитное поле распространяется в пространстве в виде волн, фазовая скорость которых равна:

где – скорость света в вакууме, , – электрическая и магнитная постоянные, , – соответственно диэлектрическая и магнитная проницаемость среды.

2. Электромагнитные волны – поперечные волны. Векторы Е и Н поля электромагнитной волны взаимно перпендикулярны друг другу. Вектор скорости волны и векторы Е и Н образуют правую тройку векторов (Рисунок 2.1.4).

Для сравнения ориентации тройки векторов , Е и Н на рисунке приведено расположение осей декартовой системы координат. Такое сопоставление уместно и в дальнейшем будет использовано для определения проекций векторов Е и Н на координатные оси.

Рисунок 2.1.4

Взаимно перпендикулярные векторы Е и Н колеблются в одной фазе (их колебания синфазные). Модули этих векторов связаны соотношением:

которое справедливо для любой бегущей электромагнитной волны независимо от формы ее волновых поверхностей.

3. По форме волновых поверхностей волны могут быть плоские, эллиптические, сферические и т.д..

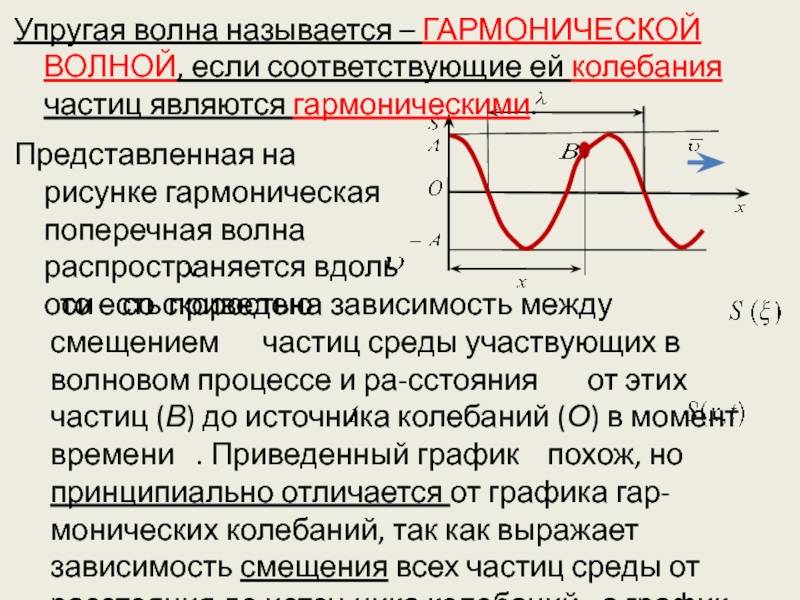
Монохроматической волной называется электромагнитная волна одной определенной частоты. Монохроматическая волна не ограничена в пространстве и во времени. В каждой точке электромагнитного поля монохроматической волны проекции векторов Е и Н на оси координат совершают гармонические колебания одинаковой частоты . Например, для плоской монохроматической волны, распространяющейся вдоль положительного направления оси ОУ, как показано на рисунке 2.1.3.,ее уравнение имеет вид:

Такие волны называются плоско (или линейно) поляризованными волнами.

Плоскость, в которой происходит колебание вектора Е называют плоскостью поляризации линейно поляризованной волны, а плоскость колебаний вектора Н – плоскостью колебаний. Ранее эти названия были обратными (см. ).

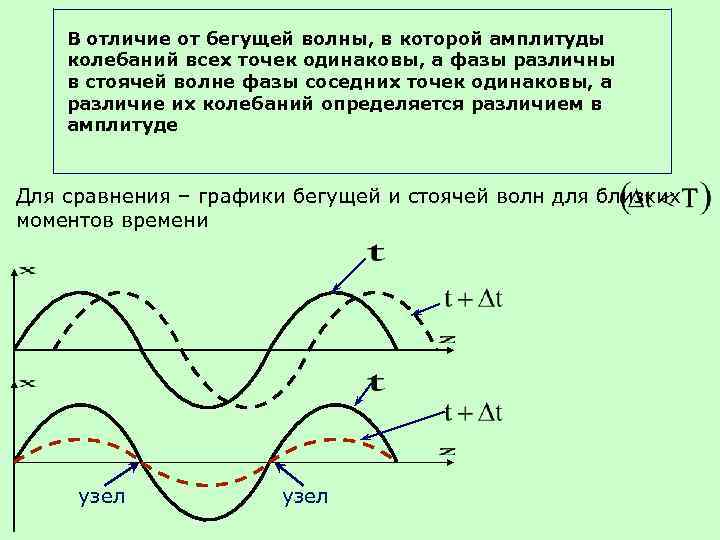
4. Все сказанное о стоячих волнах в упругих средах относится и к электромагнитным волнам. В этом случае, однако, волна характеризуется не одним вектором, а двумя взаимно перпендикулярными векторами Е и Н.

Стоячая электромагнитная волна состоит из двух стоячих волн – магнитной и электрической, колебания которых сдвинуты по фазе на .

5. Энергия электромагнитных волн. Объемная плотность энергии электромагнитного поля в линейной изотропной среде задается соотношением: с – скорость света в вакууме.

В случае плоской линейно поляризованной монохроматической волны, распространяющейся вдоль положительного направления ОY, напряженность электрического поля задается уравнением:

соответственно объемная плотность энергии этой волны

Значение объемной плотности энергии волны меняется за период от 0 до .Среднее за период значение энергии равно:

.

6. Вектор плотности потока энергии электромагнитной волны называется вектором Умова – Пойнтинга:

Для линейно поляризованной монохроматической волны вектор Пойнтинга направлен в сторону распространения волны и численно равен:

Интенсивность электромагнитной волны равна модулю среднего значения вектора Пойнтинга за период его полного колебания:

Интенсивностью электромагнитной волны называется физическая величина, численно равная энергии, переносимая волной за единицу времени через единицу площади поверхности, расположенной перпендикулярно к направлению распространения волны.

Интенсивность бегущей монохроматической волны: – фазовая скорость волны, среднее значение объемной плотности энергии поля волны.

Интенсивность света (электромагнитных волн, рассматриваемых в оптике) прямо пропорциональна квадрату амплитуды колебаний вектора напряженности Е поля световой волны.

Неоднородные среды, преломление и отражение волн

Рис. 3. Отражённая и преломлённая волны на плоской границе раздела двух сред.

Пло­ские бе­гу­щие В., стро­го го­во­ря, мо­гут су­ще­ст­во­вать толь­ко в од­но­род­ном про­стран­ст­ве. Ко­гда име­ет­ся рез­кая (в мас­шта­бе дли­ны вол­ны $λ$) гра­ни­ца раз­де­ла двух сред, воз­ни­ка­ет от­ра­же­ние волн и пре­лом­ле­ние волн (их про­ник­но­ве­ние во вто­рую сре­ду) (рис. 3). Ес­ли па­даю­щая В. и са­ма гра­ни­ца пло­ские, то пло­ски­ми бу­дут про­шед­шая и от­ра­жён­ная В. Связь па­ра­мет­ров этих В. оп­ре­де­ля­ет­ся гра­нич­ны­ми ус­ло­вия­ми, вы­те­каю­щи­ми из урав­не­ний ди­на­ми­ки со­от­вет­ст­вую­ще­го вол­но­во­го по­ля. В ча­ст­но­сти, для элек­тро­маг­нит­ных В. – это ус­ло­вия не­пре­рыв­но­сти тан­ген­ци­аль­ных ком­по­нент век­то­ров на­пря­жён­но­сти элек­трич. и маг­нит­но­го по­лей, в слу­чае уп­ру­гих В. – ус­ло­вия не­пре­рыв­но­сти дав­ле­ния и ко­ле­ба­тель­но­го сме­ще­ния час­тиц сре­ды по обе сто­ро­ны от гра­ни­цы. В изо­троп­ных сре­дах угол от­ра­же­ния $α_{отр}$ ра­вен уг­лу па­де­ния $α_0$, а угол пре­лом­ле­ния $α_{пр}$ удов­ле­тво­ря­ет за­ко­ну Снел­ла: $v_2sina_0=v_1sina_{пр}$. Для элек­тро­маг­нит­ных В. в не­про­во­дя­щей и не­маг­нит­ной сре­де ко­эф­фи­ци­ен­ты от­ра­же­ния и пре­лом­ле­ния оп­ре­де­ля­ют­ся Фре­не­ля фор­му­ла­ми. Эти ко­эф­фи­ци­ен­ты ока­зы­ва­ют­ся раз­лич­ны­ми для раз­ных по­ля­ри­за­ций па­даю­щей В. Ес­ли век­тор на­пря­жён­но­сти элек­трич. по­ля па­даю­щей В. ле­жит в плос­ко­сти па­де­ния, то при уг­ле па­де­ния $α_0$ та­ком, что вы­пол­ня­ет­ся ус­ло­вие $tga_0=n_2/n_1(n_1, n_2$ – по­ка­за­те­ли пре­лом­ле­ния сред), от­ра­жён­ная В. не воз­ни­ка­ет (см. Брю­сте­ра за­кон), то­гда как для дру­гой по­ля­ри­за­ции (элек­трич. по­ле пер­пен­ди­ку­ляр­но плос­ко­сти па­де­ния) от­ра­же­ние есть все­гда. В ре­зуль­та­те при от­ра­же­нии ме­ня­ет­ся ха­рак­тер по­ля­ри­за­ции В. В ани­зо­троп­ных сре­дах про­шед­шие В. раз­ных по­ля­ри­за­ций име­ют раз­ные уг­лы пре­лом­ле­ния (см. Двой­ное лу­че­пре­лом­ле­ние). Силь­ное влия­ние на от­ра­жа­тель­ную спо­соб­ность ма­те­риа­лов ока­зы­ва­ет их элек­трич. про­во­ди­мость; в ча­ст­но­сти, боль­шин­ст­во ме­тал­лов яв­ля­ют­ся хо­ро­ши­ми от­ра­жа­те­ля­ми в оп­тич. и ра­дио­диа­па­зо­нах.

По­сле­до­ва­тель­ные от­ра­же­ния В. в на­прав­ле­нии их рас­про­стра­не­ния от двух или боль­ше­го чис­ла по­верх­но­стей мо­гут при­вес­ти к их вол­но­вод­но­му рас­про­стра­не­нию. Вол­но­во­ды ши­ро­ко при­ме­ня­ют­ся в ра­дио- и оп­ти­че­ском диа­па­зо­нах, а так­же в аку­сти­ке. Ис­поль­зуя не­сколь­ко хо­ро­шо от­ра­жаю­щих по­верх­но­стей, мож­но соз­да­вать ре­зо­на­то­ры, вол­но­вое по­ле ко­то­рых замк­ну­то в ог­ра­ни­чен­ном объ­ё­ме. Про­стей­ший при­мер та­ко­го ре­зо­на­то­ра для элек­тро­маг­нит­ных В. (час­то при­ме­няе­мый в оп­тич. диа­па­зо­не, в т. ч. в ла­зе­рах) – ин­тер­фе­ро­метр Фаб­ри – Пе­ро, пред­став­ляю­щий со­бой сис­те­му из двух па­рал­лель­ных зер­кал, ме­ж­ду ко­то­ры­ми ус­та­нав­ли­ва­ет­ся стоя­чая вол­на. При иде­аль­но про­во­дя­щих зер­ка­лах на их по­верх­но­стях ока­зы­ва­ют­ся уз­лы элек­трич. по­ля, по­это­му внут­ри та­ко­го ре­зо­на­то­ра мо­гут су­ще­ст­во­вать лишь В. с дис­крет­ны­ми зна­че­ния­ми вол­но­во­го чис­ла.

Ес­ли же сре­да яв­ля­ет­ся плав­но не­од­но­род­ной, то вол­но­вое по­ле мож­но счи­тать «ква­зи­п­ло­ским» – на рас­стоя­ни­ях по­ряд­ка $λ$ из­ме­не­ния ам­пли­ту­ды $A$ и вол­но­во­го век­то­ра $𝑘$ бу­дут дос­та­точ­но ма­лы­ми. В та­ких слу­ча­ях ши­ро­ко ис­поль­зу­ет­ся при­бли­же­ние гео­мет­ри­че­ской оп­ти­ки, в ос­но­ве ко­то­рой ле­жит пред­став­ле­ние вол­но­во­го по­ля в ви­де на­бо­ра не­за­ви­си­мых лу­чей. В изо­троп­ной сре­де на­прав­ле­ние лу­ча сов­па­да­ет с вол­но­вым век­то­ром $𝑘$, плав­ное пре­лом­ле­ние лу­ча в не­од­но­род­ной сре­де на­зы­ва­ет­ся ре­фрак­ци­ей. Тер­мин «гео­мет­ри­че­ская оп­ти­ка» обыч­но ис­поль­зу­ют не толь­ко для све­то­вых В., но и для В. лю­бой фи­зич. при­ро­ды (в аку­сти­ке ана­ло­гич­ное при­бли­же­ние на­зы­ва­ет­ся гео­мет­ри­че­ской аку­сти­кой). Реф­рак­ция В. в сре­де с плав­ным из­ме­не­ни­ем по­ка­за­те­ля пре­лом­ле­ния в по­пе­реч­ном на­прав­ле­нии так­же мо­жет при­вес­ти к вол­но­вод­но­му рас­про­стра­не­нию.

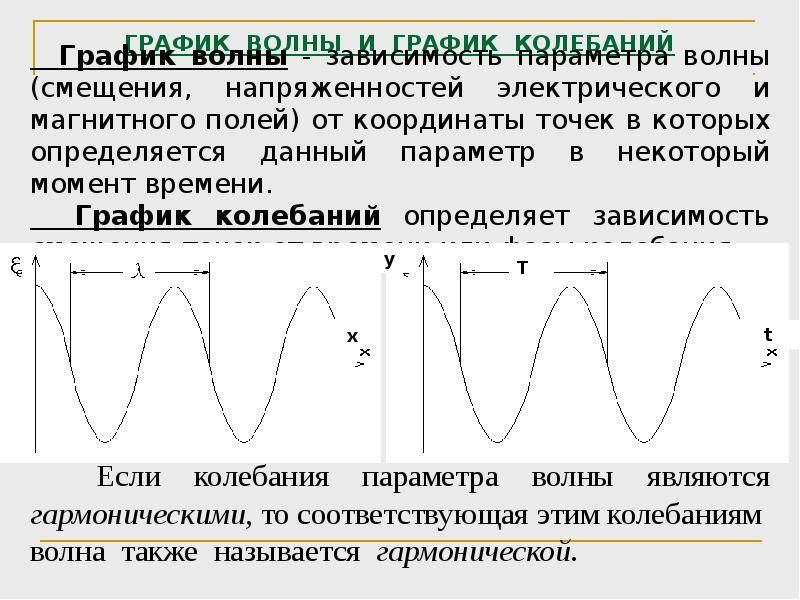
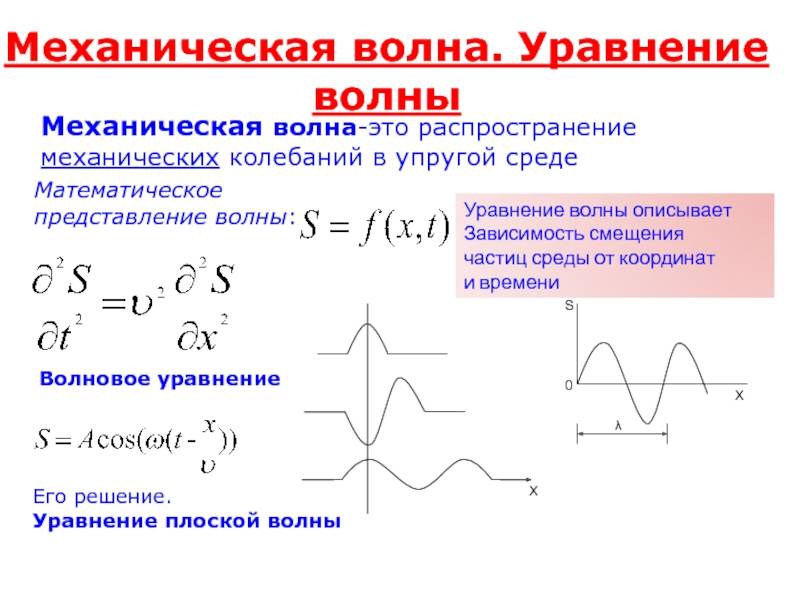
Гармонические колебания и волны

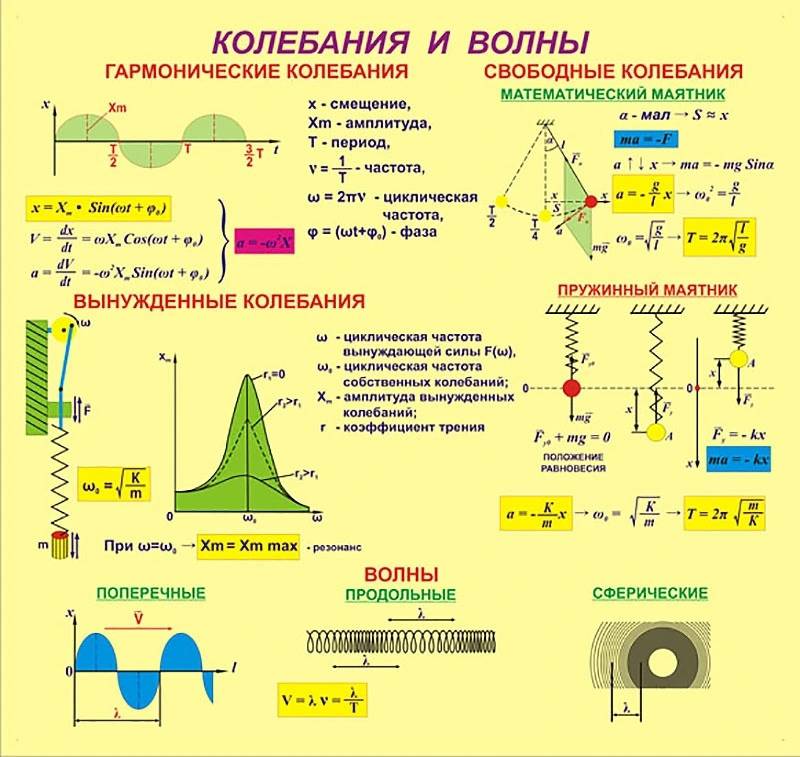
При изучении колебаний можно убедиться, что большинство из них совершаются по простому закону круговых математических функций – синуса или косинуса. Такие колебания называются гармоническими. В математике доказывается, что любые колебания можно представить бесконечной суммой гармонических составляющих. Поэтому в первую очередь изучаются именно они.

Формула механических колебаний и волн представляет собой следующее соотношение:

$$X=Asin(\omega t+\phi)$$

где:

• $X$ – координата колеблющейся точки в момент времени $t$.
• $А$ – амплитуда колебаний, максимальное отклонение точки в процессе колебания.
• $\omega$ – частота колебаний, «скорость», с которой они совершаются.
• $\phi$ – начальная фаза колебаний, начальное положение точки в момент времени $t=0$

Время, за которое совершается одно полное колебание, называется периодом колебаний $T$:

$$T={2\pi\over\omega}$$

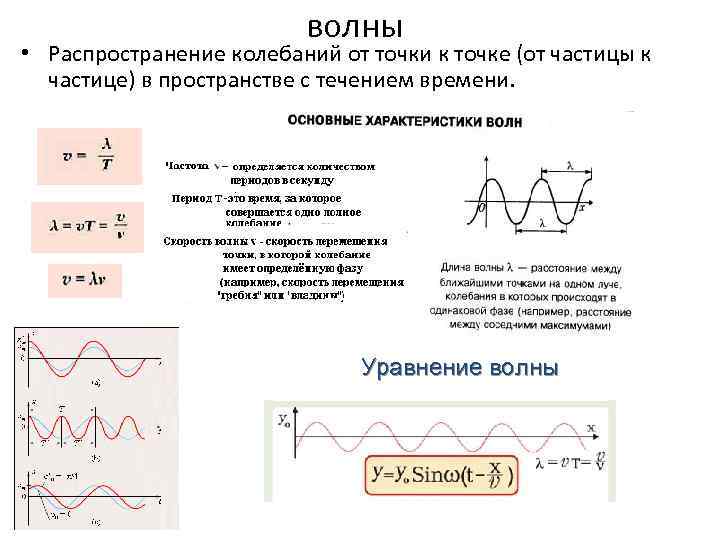
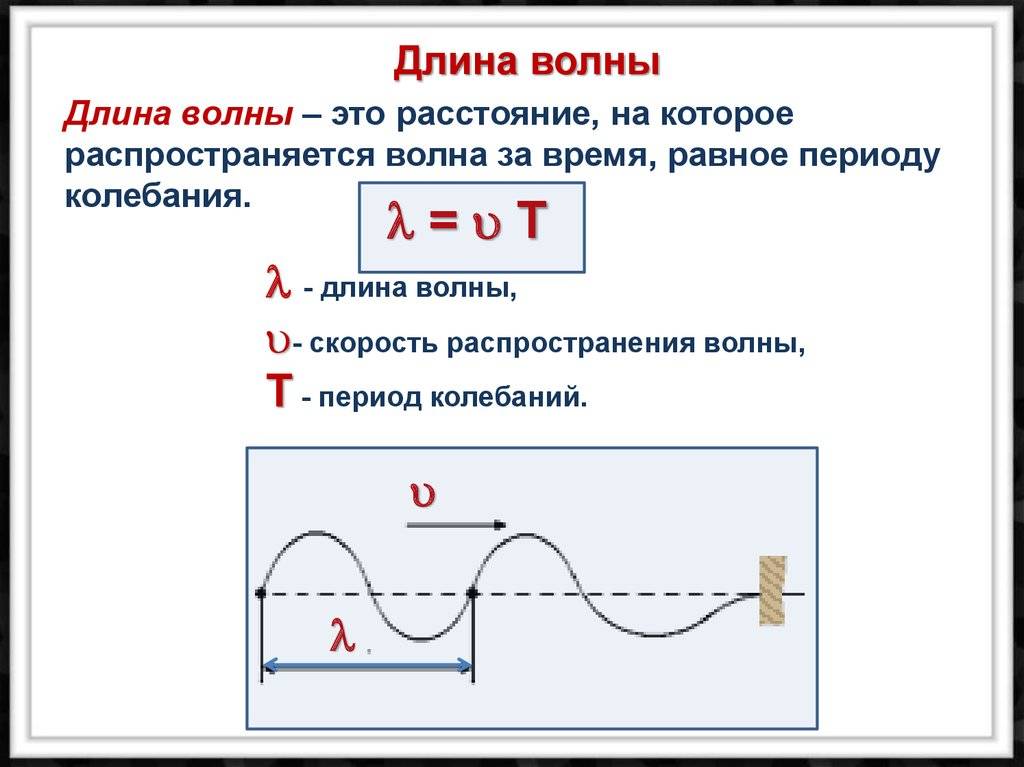
Распространение колебаний в виде волн происходит с конечной скоростью $v$. А значит, точки с одинаковой фазой (с одинаковым отклонением от равновесия), будут находиться на некотором расстоянии друг от друга, называемым длиной волны $\lambda$:

$$\lambda = vT$$

Рис. 3. График частота период фаза длина волны.

Механические волны – это чаще всего звуковые колебания. Скорость звука в различных средах меняется от десятков метров в секунду (в разреженных газах при низкой температуре) до километров в секунду (в высокоупругих средах, например в металлах) .

Что мы узнали?

Механические колебания представляют собой периодические перемещения в пространстве различных точек системы вокруг точки равновесия. Если такие перемещения распространяются со временем от одной точки системы к другим – то в системе возникает механическая волна.

1. /10

   Вопрос 1 из 10

Механические волны

Во многих случаях отдельные точки системы, хотя и совершают периодические колебания одинаковой амплитуды и частоты, делают это несинхронно. В первый момент воздействия на систему, из положения равновесия выходят только некоторые точки. Эти точки влияют на соседние, соседние точки тоже начинают выходить из положения равновесия, но делают это с некоторой временной задержкой. В свою очередь эти точки выводят из положения равновесия более далекие точки. В результате к тому времени, как первая точка начнет возвращаться к положению равновесия, другие точки системы будут все еще увеличивать отклонение. Причем, чем дальше точка будет находиться от первоначальной, тем больше будет ее запаздывание.

Таким образом, в системе возникает распространяющийся колебательный процесс, называемый волной. Примерами механических колебаний и волн могут быть волны на поверхности воды, звуковые волны и т. д.

Рис. 2. Распространение механических волн.

Разница между волной и колебаниями

Волны и колебания — традиционные явления в мире который нас окружает. Рассмотрим, что они представляют из себя и чем отличается волна от колебаний.

Обозначение

Волна — недовольство, появившееся в какой-нибудь обстановке и распространяющееся в ней с каким то периодом.Колебания — движения возвратно-поступательного характера, совершаемые некоторым телом или частичками.

Сравнение

И в том и в ином случае происходит процесс перемещения. Но отличие волны от колебаний состоит в характере подобного движения.
Волне присуще распространение на некоторое расстояние относительно места ее проявления. При этом встречается чередование самых больших и минимум показателей (к примеру, плотности или температуры).
В геометрическом изображении подобного явления присутствуют гребни и понижения.
Волна может появляться в самых различных средах. Ее легко увидеть, к примеру, бросив в воду массивный предмет. В толще земли работают сейсмические волны, в воздухе — световые.

Отличительным свойством аналогичных возмущений, какая бы ни была их природа, считается перемещение энергии из одной зоны в иную. Вещество же при этом, в основном, не переносится, хотя подобный вариант не исключен.
А в это время при колебаниях отсутствует протяженное перемещение энергии. Тут происходит переход последней то в одну, то в иную форму.
Сам процесс выполняется в маленьком пространстве и отличается иногда повторяющимся изменением того состояния системы, которое она принимает относительно точки равновесия.
При механических колебаниях встречается перемещение вещества (маятник, качели, груз на пружине). При электро-магнитных — передвигаются только частицы.

В последнем варианте примером будет процесс, происходящий в колебательном контуре.
Необходимо выделить, что обсуждаемые явления не рассматриваются изолированными один от одного. Волну можно образно представить как «растянутое» колебание, в котором, при чередовании фаз, действует уже не одна материальная точка, а много подобных смежных элементов.
Лучше понять, в чем разница между волной и колебаниями, поможет и следующий пример. Представим, что тело в механической системе под действием силы выводится из равновесия.
Появляется движение объекта с постоянной сменой направления, или колебание. В процесс вовлекается внешняя среда.

Вещество в ней начинает сжиматься и разряжаться.
Недовольство распространяется с конкретной скоростью все дальше от источника. Этот процесс уже считается волновым.

Волна

Между тем волны – это распространяющиеся колебания. В отличие от колебаний, движение которых сосредоточено в точке равновесия, волны перемещаются из одной точки в другую. Посмотрите на изображение ниже.

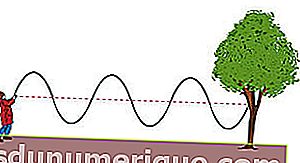
На картинке выше изображен ребенок, привязывающий конец веревки к ветке дерева. Затем ребенок регулярно трясет другим концом веревки вверх и вниз. Видно, что со временем вибрация распространяется по веревке, пока не достигает конца веревки, который привязан и образует волну. Из этой иллюстрации мы получаем определение, что распространение вибрации называется волной.

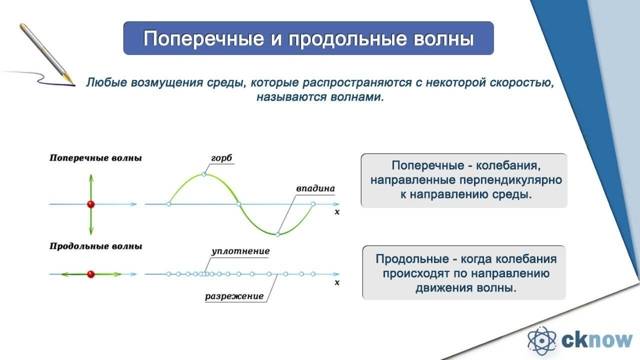
В зависимости от направления распространения и направления вибрации волны делятся на два типа, а именно поперечные волны и продольные волны.

Поперечные волны – это волны, направление распространения которых перпендикулярно направлению вибрации, как в примере выше. Видно, что волны, образующиеся на канате, являются поперечными волнами, направление распространения которых перпендикулярно направлению колебаний. Есть несколько примеров поперечных волн, а именно волны на веревках и световые волны.

Между тем, продольные волны – это волны, направление распространения которых параллельно направлению колебаний. Предположим, что пружина с одним концом, скрепленным горизонтально, находится в равновесии. Затем пружина вытягивается и отпускается, вызывая в ней колебания и волны. Видно, что волна, сформированная на пружине, представляет собой продольную волну, направление распространения которой параллельно направлению колебаний.

Некоторыми примерами продольных волн являются волны в пружинах и звуковые волны.

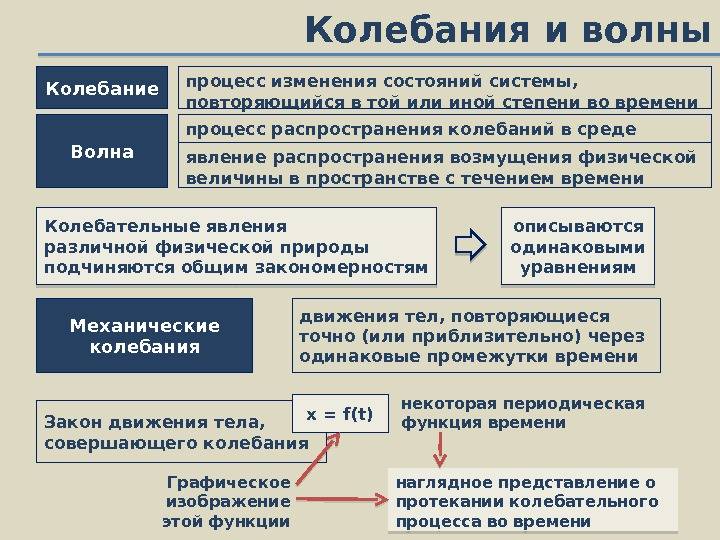
Колебания и волны

Колебания — повторяющийся в самой разной степени во времени процесс изменения состояний системы. К примеру, при колебаниях маятника повторяются отклонения его в ту и обратную сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.
Колебания практически всегда связаны с попеременным изменением энергии одной формы проявления в иную форму.
Отличие колебания от волны.
Колебания разной физической природы имеют много общих закономерностей и тесно связаны c волнами. Благодаря этому исследованиями таких закономерностей занимается обобщённая доктрина колебаний и волн.

Значительное отличие от волн: при колебаниях не происходит переноса энергии, это, так сказать, «местные» изменения энергии.Спецификации колебаний
Выделение разнообразных видов колебаний зависит от свойства, которое хотят выделить.
Для подчёркивания различной физической природы колеблющихся систем (осцилляторов) выделяют, к примеру, колебания:

• механичные (звук, вибрация);
• электромагнитные (свет, радиоволны, тепловые);
• конфигурации перечисленных выше;

По характеру взаимные действия с внешней средой:

• вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия;
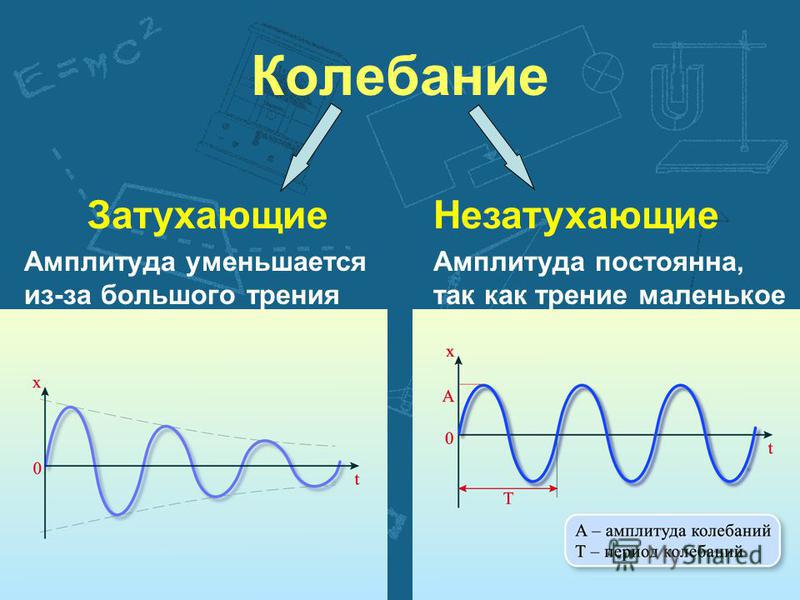
• свои или свободные — колебания при отсутствии внешних сил, когда система, после первоначального воздействия внешней силы, дается для себя (в настоящих условиях свободные колебания всегда затухающие);
• автоколебания — колебания, при которых система имеет запас возможный энергии и она расходуется на совершение колебаний (пример подобной системы — механичные часы).

Характеристики колебаний

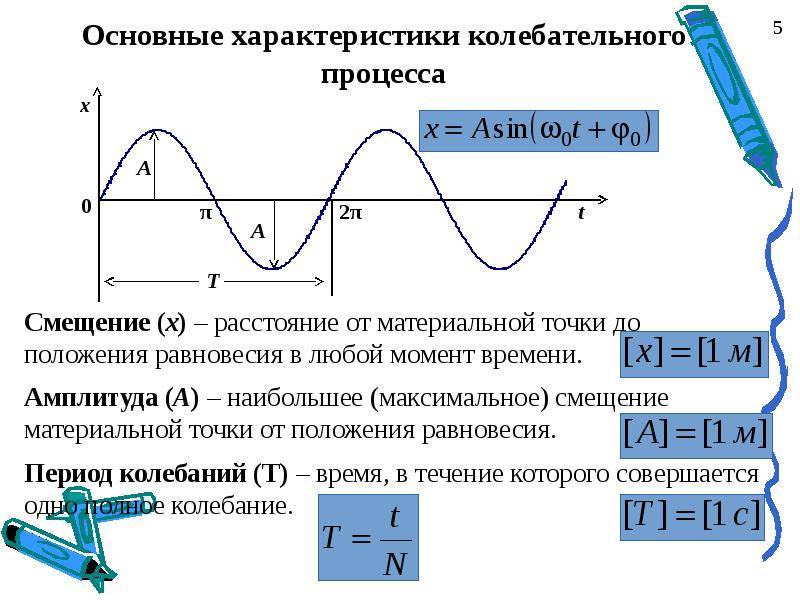
Амплитуда(м) — максимальное отклонение колеблющейся величины от некоторого среднего её значения для системы.
Зазор времени(сек), через который повторяются какие-нибудь критерии состояния системы (система совершает одно полное колебание), именуют временем колебаний.
Число колебаний в единицу времени именуется частотой колебаний(Гц, сек-1).
Период колебанийи частота– обратные величины;
В круговых или циклических процессах заместо характеристики «частота» применяется понятие круговая или циклическая частота(Гц, сек-1, об/сек), показывающая число колебаний за время 2?:
Фаза колебаний — определяет смещение практически в любое время времени, т.е. определяет состояние колебательной системы.
Меркурий — ближайшая к Солнцу планета. Римляне в древние времена считали Меркурия покровителем торговли, туристов и воров, и еще вестником богов. В этом нет ничего удивительного, что маленькая планета, быстро перемещающаяся по небу вслед за Солнцем, обрела его имя. Меркурий был известен еще с древности, впрочем древние астрологи не сразу убедились, что вечером и утром …

Измерение времени

Дать ответ «что такое время» непросто. В самом общем виде можно сказать, что время — это постоянная вереница сменяющих друг друга явлений. Ключевое свойство времени заключается в том, что оно продолжается, течет безостановочно. Пространство можно уберечь, но время остановить нереально. Время необратимо — поездки на машине времени в прошлое невозможны. «Нельзя …

Слог + картинка

Слог + картинка На шаге самостоятельного чтения применяется упражнение “Слог + картинка”. Подобного рода задания нечасто встречаются в учебных пособиях, однако они крайне полезны, так как помогают раннему появлению осмысленного чтения. Ребенку предлагается объединить картинку со слогом, на который начинается ее наименование. В ином варианте задания под …

Патрокл — заблудившаяся комета

Астрологи из университета Berkeley (Калифорния), работая с коллегами из Франции на телескопе ми. Вильяма Кека (Гавайи), провели подробные наблюдения двойного астероида Patroclus (Патрокл), который обращается вокруг Солнечного света по такой же орбите, что и Юпитер. Отделав данные, ученые поняли, что и сам астроид и его компаньон, возможно, сформированы в основном из водяного …

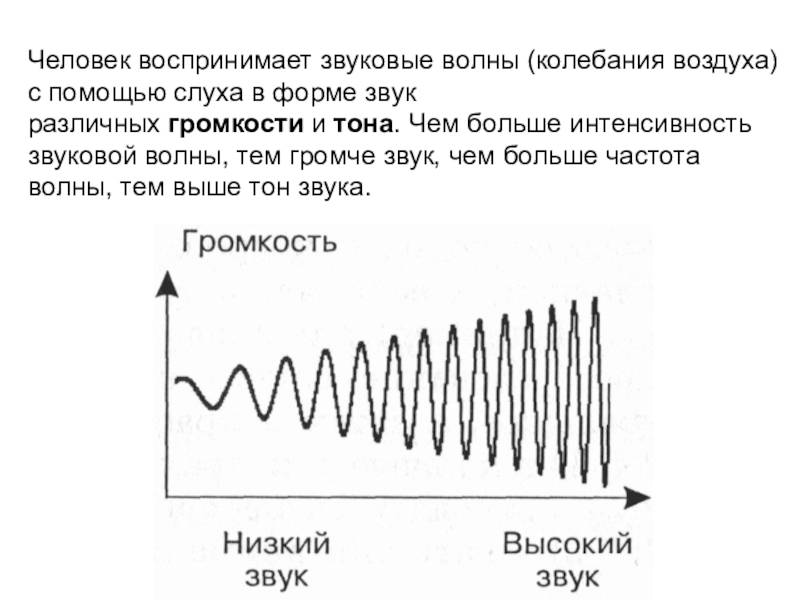
Звуковые волны

1. Важным видом продольных волн являются звуковые волны. Так называются волны с частотами 17 – 20000 Гц. Учение о звуке называется акустикой. В акустике изучаются волны, которые распространяются не только в воздухе, но и в любой другой среде. Упругие волны с частотой ниже 17 Гц называются инфразвуком, а с частотой выше 20000 Гц – ультразвуком.

Звуковые волны – упругие колебания, распространяющиеся в виде волнового процесса в газах, жидкостях, твердых телах.

2. Избыточное звуковое давление. Уравнение звуковой волны.

Уравнение упругой волны позволяет вычислить смещение любой точки пространства, по которому проходит волна, в любой момент времени. Но как говорить о смещении частиц воздуха или жидкости от положения равновесия? Звук, распространяясь в жидкости или газе, создает области сжатия и разряжение среды, в которых давление соответственно повышается или понижается по сравнению с давлением невозмущенной среды.

Если – давление и плотность невозмущенной среды (среды, по которой не проходит волна), а – давление и плотность среды при распространении в ней волнового процесса, то величина называется избыточным давлением. Величина есть максимальное значение избыточное давление (амплитуда избыточного давления).

Изменение избыточного давления для плоской звуковой волны (т.е. уравнение плоской звуковой волны) имеет вид:

,

где y – расстояние от источника колебаний точки, избыточное давление в которой мы определяем в момент времени t.

Если ввести величину избыточной плотности и ее амплитуды так же, как мы вводили величину избыточного звукового давления, то уравнение плоской звуковой волны можно было бы записать так: . 3. Объективные и субъективные характеристики звука.

Само слово “звук” отражает два различных, но взаимосвязанных понятия: 1)звук как физическое явление; 2)звук – то восприятие, которое испытывает слуховой аппарат (человеческое ухо) и ощущения, возникающие у него при этом. Соответственно характеристики звука делятся на объективные, которые могут быть измерены физической аппаратурой, и субъективные, определяемые восприятием данного звука человеком.

К объективным (физическим) характеристикам звука относятся характеристики, которые описывают любой волновой процесс: частота, интенсивность и спектральный состав. В таблицу 3 включены сравнительные данные объективных и субъективных характеристик.

Таблица 3.

Субъективные Характеристики	Объективные характеристики
Высота звука	Высота звука определяется частотой волны
Тембр (окраска звука)	Тембр звука определяется его спектром
Громкость (сила звука)	Сила звука определяется нтенсивностью волны (или квадратом ее амплитуды)

Остановимся на некоторых определениях.

Частота звука измеряется числом колебаний частиц среды, участвующих в волновом процессе, в 1 секунду.

Интенсивность волны измеряется энергией, переносимой волной в единицу времени через единичную площадь (расположенную перпендикулярно направлению распространению волны).

Спектральный состав (спектр) звука указывает из каких колебаний состоит данный звук и как распределены амплитуды между отдельными его составляющими.

Различают сплошные и линейчатые спектры. Для субъективной оценки громкости используются величины, называемые уровнем силы звука и уровнем громкости. Все акустические величины и их размерности в СИ приведены в приложении.

Применение волновых процессов в разных областях

Волновые процессы играют важную роль во многих областях науки и техники. Вот некоторые из них:

1. Физика: Волны используются для изучения свойств вещества и физических законов. Они помогают в исследовании электромагнитного спектра, а также распространения звука и света.

2. Медицина: Ультразвуковые волны применяются для обнаружения и лечения заболеваний. Они могут помочь в диагностике и лечении различных состояний, таких как рак, кардиоваскулярные заболевания и беременность.

3. Информационные технологии: Волны используются для передачи информации по различным каналам связи, таким как радиоволны, оптические волокна и сигналы преобразования.

4. Геофизика: Исследование волновых процессов позволяет ученым изучать земное ядро, его состав и структуру. Это дает возможность предсказывать землетрясения и изучать геологические процессы.

5. Инженерия: Волновые процессы играют важную роль в различных областях инженерии, включая акустику, электронику, механику и оптику. Они помогают в создании новых технологий и устройств.

Применение волновых процессов в этих областях продолжает расти, открывая новые возможности для научных исследований и технологического развития.

Скорость распространения волны

Под скоростью распространения волны понимают скорость распространения колебаний (возмущения). Так же можно сказать, что скорость продольной или поперечной волны – это скорость переноса энергии бегущей волны. Скорость, как и всегда, обозначается буквой  ν (в данном случае, скорость – вектор, в эту величину включается и модуль, и направление движения; если в условиях конкретной задачи необходим только модуль скорости, он обозначается ν).

Волны, распространяющиеся в пространстве, удобно рассматривать, используя функции. Обратимся к примеру, с пружиной, представленному ранее. Вдоль пружины можно выбрать координатную ось х. Волны, бегущие в пружине – это волны уплотнения и растяжения. Тогда можно задать относительную деформацию ε как функцию от координаты х:

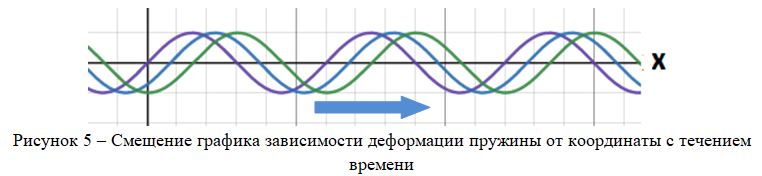
То есть, пользуясь этой функцией, мы сможем вычислить деформацию в каждой точке пружины, а также можно построить график – рисунок 4.

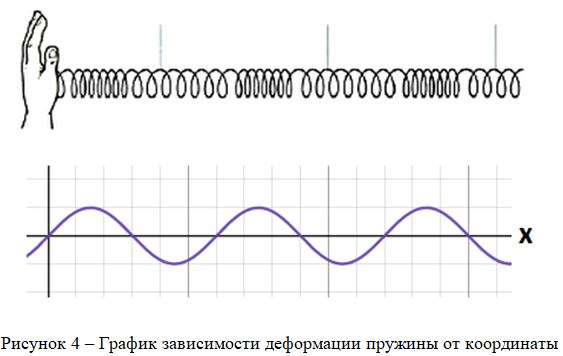
Как уже говорилось ранее, волна распространяется (бежит) по пружине с течением времени (t). Скорость бегущей волны v. Чтобы учесть это, воспользуемся свойством смещения графика функции, и зададим плотность так:

График функции, заданной в таком виде, при равномерном увеличении t будет ползти вправо. То есть каждая точка графика будет двигаться вправо со скоростью v (рисунок 5).

Для задания волны, бегущей влево, нужно задать смещение с противоположным знаком:

Приведенные выражения называются уравнениями бегущей волны. Удобство такого рассмотрение заключается в том, что наложение множества волн с разными характеристиками можно рассматривать просто как математическую функцию, и использовать для этого весь мат. аппарат. В программе старших классах будет разобрано, как это применяется для исследования свойств одной волны и наложения двух и трех волн.А пока достаточно знать, как по виду функции определить, в каком направлении движется волна.

*Математическое отступление.

Напомним, что математическая функция в узком смысле – это закон, который в соответствие одному числу ставим другое. В записи:

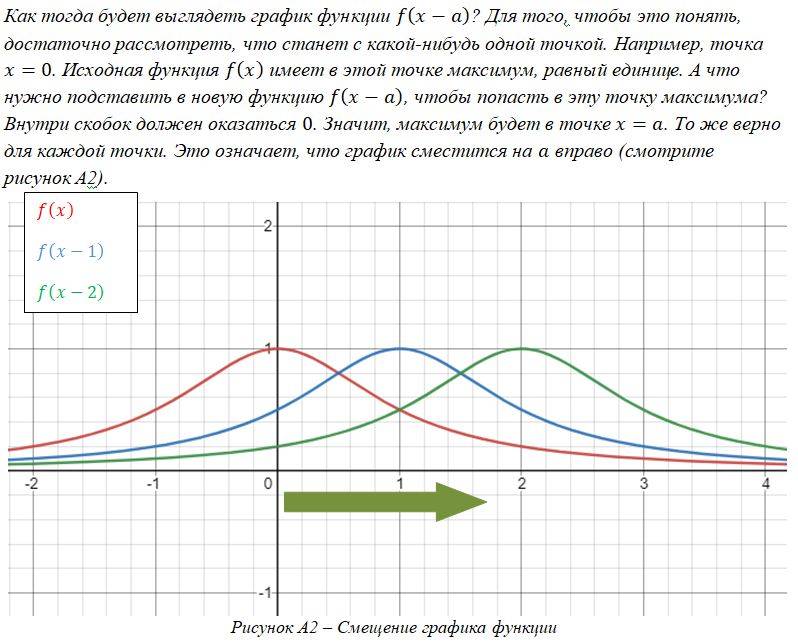
Почему нельзя считать колебания маятника волной?

Волна — недовольство состояния среды (изменение), которое распространяется в этой обстановке, перенося с собой энергию.
Говоря по другому, пространственное чередование максимумов и минимумов любой пространственной величины (температура, плотность, напряженность электрического поля и т.д.), которое меняется с каким то периодом, и есть волна.
Более верным определением волны будет следующим: Волна — есть явление распространения в пространстве со временем возмущения физической величины.
Не зависимо от природы волны исполнение переноса энергии происходит без переноса вещества. Перенос вещества может случиться только в роли побочного эффекта.
Процесс , в котором имеют место быть только ”местные” изменения энергии, считается важным различием волны от колебания. Волны в большинстве случаев могут отдаляться на порядочные расстояния относительно места, в котором они возникли.
В последствие этого волнам иногда дают подобное название, как ”колебание, оторвавшееся от излучателя”.
Маятником именуют твёрдое тело, которое под действием приложенных сил совершает колебания возле неподвижной точки либо оси. В физике как правило имеют понятие маятника, как тела, совершающего колебания под действием силы тяжести, ось которого не идет через центр тяжести данного тела.
Очень простым маятником считается маленькой большой и тяжелый груз С, который подвешен на нити, имеющей длину l.
Если условиться, что эта нить нерастяжима, и проигнорировать размерами груза по сравнению с длиной нити, а еще массой нити по сравнению с массой груза, то груз, подвешенный на данную нить можно рассматривать как материальную точку, которая расположена на неизменном расстоянии l от точки подвеса О.
Данный маятник называется математического маятника. Принимая к сведению перечисленные выше условия, можно дать ответ, почему колебания математического маятника нельзя считать волной?

В случае, когда колеблющееся тело нельзя рассмотреть как материальную точку, маятник будет именоваться физическим.
? Открой Секрет ? Почему нельзя заряжать телефон ночью?
Значительная часть волн по собственной сути новыми физическими явлениями не считаются, если только относительным наименованием для конкретного вида коллективного движения.
Если в объеме газа возникла волна звука, то это абсолютно не значит, что в этом объеме возникли некие новые физические объекты. Звуком именуют лишь особенный скоординированный вид перемещения тех же самых молекул.
По-иному говоря, значительная часть волн — это колебания некоторой среды. За рамками этой среды волны данного типа не существует (например, звук в вакууме).
Не обращая внимания на это, есть волны, не являющиеся ”зыбью” какой нибудь другой среды, а являются конкретно новыми физическими явлениями.
К примеру, электромагнитные волны в сегодняшней физике именуют не колебание какой-нибудь среды (называлась ”эфир” в девятнадцатом веке), а самостоятельное поле, способное самоподдерживаться, которое имеет особенность распространяться в вакууме. Также происходит и с волнами допустимости материальных частиц.
? Открой Секрет ? Почему нельзя скачать предмет в айтюнс?
Волнами именуют также и некоторые явления, но любая из этих волн имеет собственную индивидуальную специфику. Например, так говорят иногда о волнах горения, волнах плотности реагентов, волнах хим. реакций, волнах плотности потоков транспорта, температурных волнах, волнах допустимости электрона и других частиц.

Необходимо внимание уделить тому, что явления, которые смотрятся как волны, но которые не способны к самораспространению, не считаются волнами (например, дюны песка).

Волновые процессы

Определение 6

Волновым процессом (волной) называют процесс распространения колебаний в сплошной среде.

В волновом процессе частицы вещества не перемещаются совместно с волной, они совершают колебания у своих положений равновесия. С волной происходит передача состояния колебаний и энергия этого движения.

Основное свойство волны – это транспортировка энергии при отсутствии переноса вещества.

Определение 7

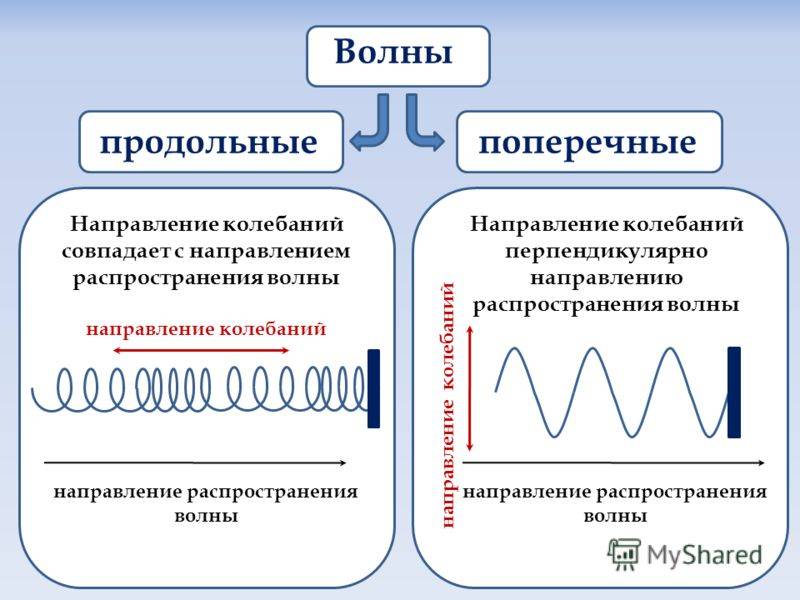
Механическими (упругими) волнами называют механические возмущения, которые распространяются в упругой среде.

Механические волны делят на:

• продольные;
• поперечные.

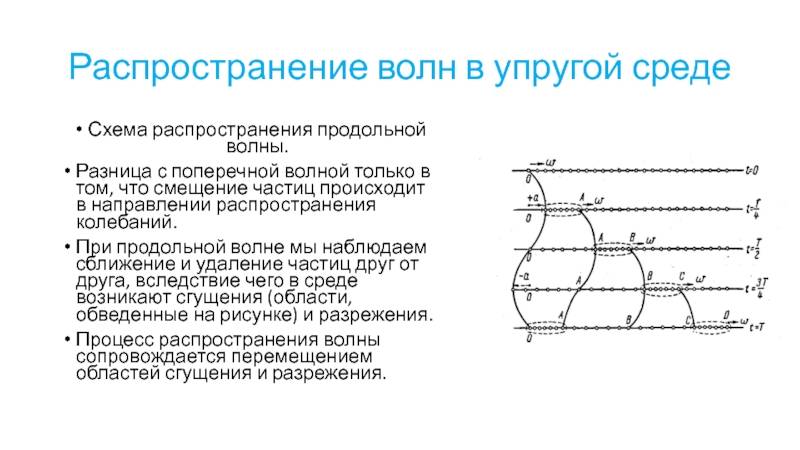
Продольными волнами являются волны, в которых частички вещества, в котором происходит распространение волны, совершают колебания вдоль направления ее распространения.

В поперечной волне частички среды колеблются в плоскостях, нормальных к направлению следования волны.

Продольные волны способны к распространению при наличии в веществах сил упругости при сжатии и растяжении. Такими веществами являются газ, жидкость и твердое тело.

Поперечные волны возможны в веществах, в которых могут возникать силы упругости при деформации сдвига. В основном к данным веществам относят твердые тела.

Механические волны называют гармоническими, если колебания частиц в ней описываются гармоническими законами.

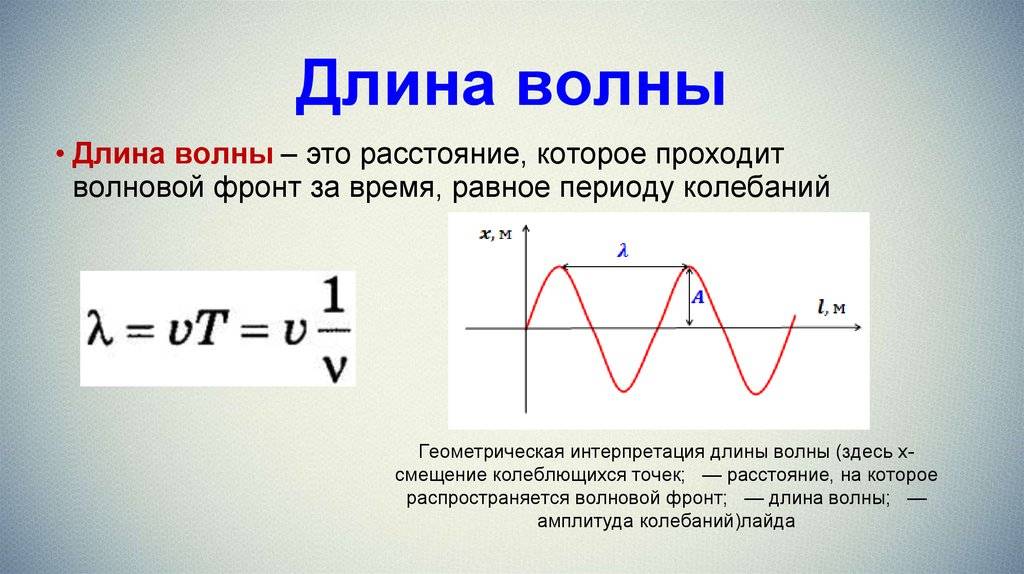
Длиной волны (\lambda) называют расстояние между самыми близкими частичками, которые совершают колебания в одной фазе.

Длина волны связана с периодом колебаний:

$\lambda = vT (2).$

Распространение колебаний в среде

Чтобы понять, что такое колебания в среде достаточно представить несколько простых примеров:

• камень бросили в воду, по поверхности воды тут же расходятся круги – это и есть колебания поверхности воды;
• игра на гитаре – струна начинает колебаться после прикосновения музыканта.

Рассмотрим простую ситуацию распространения колебаний в среде: длинная пружинка, закрепленная с одной стороны, а с другой на нее оказывается периодическое внешнее воздействие, например, равномерные толчки рукой (см. рисунок 1).

После первого толчка часть пружинки, которая находится ближе к руке, сожмется (см. рисунок 1а), а потом из-за упругих свойств пружины, разожмется, воздействуя на витки, лежащие правее первоначального сжатия (см. рисунок 1б).  Таким образом сжатие будет «продвигаться» вправо (влево – нет, так как ему мешает рука, блокирующая левый край пружины). После следующего толчка рукой образуется новое сжатие, которое тоже будет «продвигаться» вправо, потом следующее сжатие и т.д. (см. рисунок 1в).

Обобщить все сказанное можно следующим образом: колебания в среде или даже колебания среды (ведь пружинка – это среда) представляют собой некое возмущение, распространяющееся от места их возникновения без переноса вещества. Источником таких возмущений является колеблющееся тело (или некое периодическое воздействие). Такое возмущение и называется волной. Рассмотрим это явление подробнее.