Разница между векторной и скалярной величиной

Что нужно знать о векторных величинах (векторах)

Векторы характеризуются модулем и направлением в пространстве

Модулем вектора называется его числовое значение.

Вектор изображают в виде направленного отрезка (стрелки). Стрелка указывает, куда направлен вектор (рис. 14, 15). Длина стрелки характеризует модуль вектора (рис. 16). Над буквенным обозначением вектора ставят стрелку, например:  

Модуль вектора обозначают той же буквой, но без стрелки над ней или символом  Например, модуль вектора на рисунке 16 равен

Модуль любого (не равного нулю) вектора — число положительное.

Векторы равны между собой, если равны их модули и одинаковы направления

Равные векторы лежат на одной и той же прямой или на параллельных прямых и направлены в одну и ту же сторону. На рисунке 17   Однако, несмотря на равенство модулей, так как у векторов различные направления.  

Угол между векторами

Чтобы найти угол между векторами (рис. 18, а), нужно совместить их начала (рис. 18, б). Если направления векторов одинаковы, то (рис. 18, в), если противоположны, то (рис. 18, г).

Умножение вектора на число

Произведение вектора на число есть вектор Чему в равен его модуль? Куда направлен вектор

Модуль вектора равен

Если то вектор направлен так же, как вектор а если то противоположно ему.

На рисунке 19 показаны результаты умножения вектора на 2, на 0,5, на (-3) и на (-1) соответственно. 

Противоположные векторы

Вектор называется противоположным вектору если У векторов одинаковые модули, но противоположные направления (рис. 19, а, г).

Сложение векторов

В 7-м классе вы складывали силы, направленные или одинаково, или в противоположные стороны. Результатом сложения в первом случае была сила, модуль которой равен а во втором

То же самое получается и при сложении векторов  (рис. 20). Если они направлены одинаково (рис. 20, а), то их сумма имеет модуль Если же направления векторов противоположны (рис

20, б), то модуль их суммы Обратите внимание: в последнем случае вектор направлен так, как вектор с большим модулем (т. е

как вектор ).  

А как сложить векторы, направленные под любым углом друг к другу? Для этого можно использовать любое из двух следующих далее правил. 

Правило параллелограмма

Совместим начала векторов (рис. 21, а), сохраняя их направления (рис. 21, б). Построим параллелограмм ABCD, принимая векторы за его стороны. Сумма векторов есть вектор совпадающий с диагональю АС параллелограмма: (см. рис. 21, б).

Правило треугольника

Совместим конец вектора с началом вектора сохраняя их направления (рис. 21, в). Вектор проведенный из начала вектора в конец вектора  равен сумме (см. рис. 21, в).

Из рисунков 21, б и 21, в ясно, что правило треугольника и правило параллелограмма дают одинаковые результаты. А как найти разность векторов?

Вычитание векторов

Пусть начала векторов совмещены (рис. 22). Проведем вектор из конца вычитаемого вектора в конец уменьшаемого вектора Вектор есть искомая разность:  Докажите с помощью построения, что Такой способ вычитания векторов очень удобен.

Правило многоугольника

Чтобы найти сумму нескольких векторов (например, ), каждый следующий вектор нужно проводить из конца предыдущего (рис. 23). Замыкающий вектор проведенный из начала первого вектора в конец последнего есть сумма данных векторов: 

Правило многоугольника следует из правила треугольника.

Модуль суммы векторов

Не путайте модуль суммы векторов, т. е. и сумму их модулей  Равенство  выполняется только для одинаково направленных векторов (см. рис. 20, а на с. 13). Во всех остальных случаях т. е. модуль суммы векторов меньше суммы их модулей. Так получается потому, что в любом треугольнике (см. рис. 21, в) длина одной стороны меньше суммы длин двух других сторон. Проверьте это на примерах.

Нуль-вектор

Пусть вектор равен вектору Тогда их разность т. е. нуль-вектору.

Главные выводы:

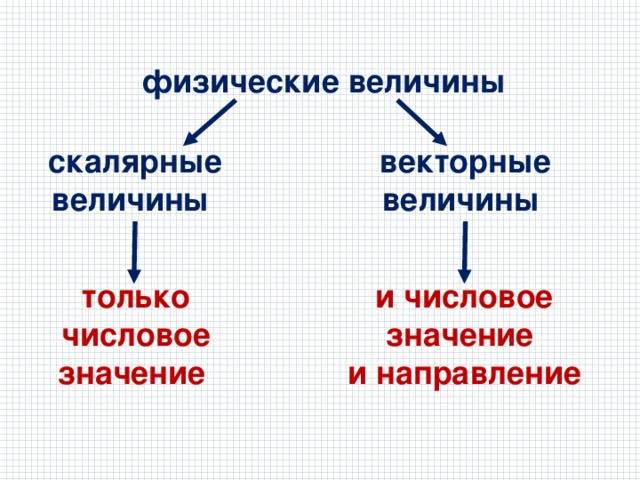
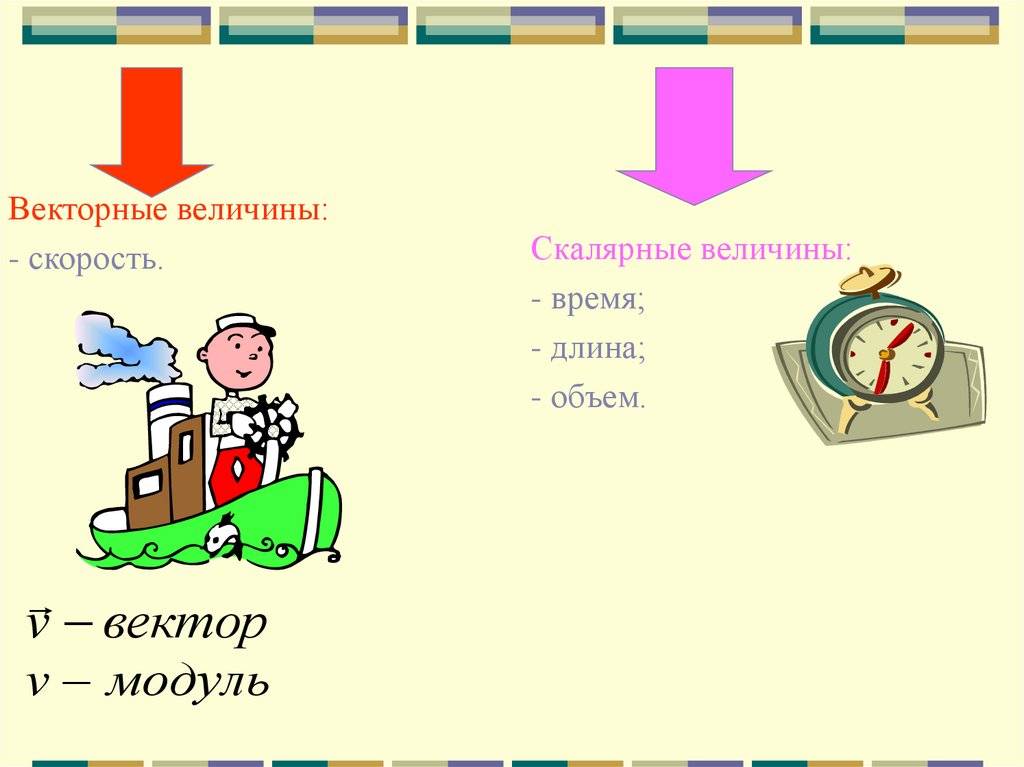
1. Векторные величины характеризуются модулем и направлением, скалярные — только числовым значением.
2. Сумму двух векторов находят по правилу параллелограмма или треугольника.
3. Разность двух векторов находят, проводя вектор из конца вычитаемого вектора в конец уменьшаемого (при совмещенных началах векторов).
4. Разность векторов можно найти как сумму
5. Произведение вектора на число есть вектор При направления векторов совпадают, а при — противоположны. Модуль вектора равен

Различия между скалярными и векторными величинами

Все физические величины можно разделить на два типа: великие скаляры и векторов. Основное различие между этими двумя типами величин состоит в том, что скаляры могут быть удовлетворительно представлены только величинами

номерединствовмера.значениечисловойнаправлениесмысл

→ скалярные величины

величиныскаляры те, которые можно записать в виде номер, за которым следует единица измерения. Другими словами, они полностью определены, если мы знаем их значение, также называемое модулем, и способы его измерения.

Примеры скалярных величин: длина, O время, а температура и макароны. Ознакомьтесь с некоторыми способами выражения этих величин:

• 1 мес. – метр; 10 см – десять сантиметров; 2мм – два миллиметра.
• 10 с – десять секунд; 15 мин – пятнадцать минут; 1 час – один час.
• 25º C – двадцать пять градусов по Цельсию; 86º F – восемьдесят шесть градусов по Фаренгейту; 10 тыс. – десять кельвинов.
• 200 г – двести грамм; 10 мг – десять миллиграммов; 2 кг – два килограмма.

Коротко:

скалярные величины они полностью определяются числом и единицей измерения.

Посмотритетакже:Все, что вам нужно знать о физике Механика, которая попадает в Enem

→ векторные величины

векторные величины должны быть выражены номер (модуль), один направление, а смысл является единствовмера. Это означает, что эти величины могут быть выражены через стрела (вектор), то есть для их определения необходимо учитывать точку зрения наблюдателя.

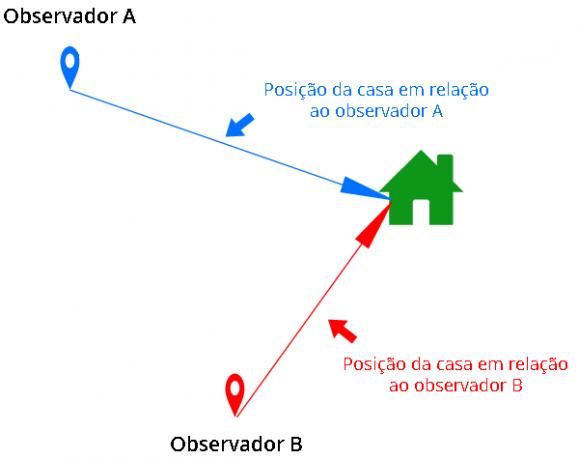На рисунке показано, что положение дома является векторной величиной, поскольку зависит от взглядов наблюдателей A и B.

Прежде чем мы продолжим обсуждение того, что такое векторные величины, необходимо понять разницу между модуль, направление а также смысл:

• Модуль: мера или размер вектора, представляющего величину вектора.
• Направление: размер пространства, который зависит от используемой системы навигации. Есть направления, такие как ширина, высота и глубина, или даже горизонтальное и вертикальное направление, или направление x, y и z (используется в декартовой системе), или даже направление восток-запад, север-юг.
• Смысл: ориентация вверх или вниз, вправо или влево, положительное или отрицательное, восток или запад, север или юг. Каждое направление имеет два направления, которые похожи на стрелки каждого вектора.

Ознакомьтесь с некоторыми примерами векторных величин:

• Должность
• Смещение
• Скорость
• Сила
• Ускорение

Что общего у всех перечисленных выше величин, помимо того, что они являются векторными? Все зависит от направление это смысл. Например, если кто-то спрашивает вас Где пекарня, недостаточно ответить, что это 50 м, необходимо установить некоторые системассылки, например, следующее:

Чтобы добраться до пекарни, поверните направо (смысл) отсюда (происхождение системы отсчета) и двигаться прямо (направление), пробегая через50 м (модуль и единица измерения).

Коротко:

векторные величины они полностью определяются числом, единицей измерения, направлением и смыслом.

Читайте тоже: Векторные операции

Что такое вектор?

Теперь мы понимаем определение вектора, который представляет собой физическую величину с величиной, а также направлением. Он представлен стрелкой, и направление этой стрелки совпадает с направлением количества.

Вектор известен как единичный вектор, если его величина равна 1, и этот единичный вектор используется для определения направления.

У вектора есть направление и величина, но нет позиции. Для вычисления каждой векторной единицы нам нужен вектор, поэтому нам нужно понимать этот термин.

Вектор используется в нашей повседневной жизни для определения местоположения объектов и людей. Первый закон Ньютона, Второй закон и Третий закон невозможно понять без использования вектора.

В таких видах спорта, как баскетбол, крикет, игроки используют вектор бейсбола. Игрок бросает мяч или стреляет в цель под углом в определенном направлении.

Vector используется в военных целях, в снарядах / траекториях и даже при проектировании американских горок.

Если вектор повернуть на угол, он изменится.

Вектор определяется по его величине и направлению. Итак, если мы делаем даже небольшое изменение его величины или направления, вектор может быть изменен. Следовательно, если мы повернем шар на некоторый угол, его направление изменится, и мы можем сказать, что вектор изменился.

Мы можем определить вектор в двухмерном и трехмерном пространстве. Благодаря этой характеристике Vector многомерные задачи могут быть решены с его помощью.

Свойства векторов

Вектор — математический элемент, представляющий собой прямой отрезок с направлением. Он обозначается либо 2 заглавными латинскими буквами, либо одной прописной. Длиной вектора является его модуль. Если длина вектора равняется 0, то он называется нулевым. Вектор, имеющий длину 1 см, именуется единичным. Длина ненулевого вектора выражается в виде расстояния между началом и концом направленного отрезка. Проекцией вектора на ось является строго положительный отрезок, сонаправленный с исходной осью. Свойства проекции:

• Произведение вектора на косинус между осью и направленным отрезком равен проекции вектора.
• Проекция на ось принимает значения меньше 0, если отрезок с осью образует тупой угол.
• Проекция на ось принимает значение больше 0, если отрезок с осью образует острый угол.

Коллинеарные векторы — отрезки, располагающиеся либо на одной прямой, либо на параллельных прямых. Нулевой вектор коллинеарен всегда. Если коллинеарные векторы направлены в одну сторону, то они называются сонаправленными. Если отрезки направлены в диаметрально противоположные стороны, то они называются противоположно направленными. Коллинеарные векторы являются равными, если они одинаковы по модулю и направлению.

С векторами также можно производить операции сложения, деления, вычитания и умножения. Чтобы сложить два вектора, необходимо от произвольной точки на плоскости отложить первый направленный отрезок и от него отложить второй вектор. Отрезок, соединяющий начало первого вектора и конец второго, будет считаться их суммой. Этот способ сложения именуется методом треугольника.

Вторым способом нахождения суммы векторов является метод параллелограмма. От произвольной точки откладываются оба направленных отрезка. Полученный рисунок нужно достроить до параллелограмма. Диагональ фигуры будет являться суммой векторов.

Для осуществления вычитания необходимо отложить от произвольной точки первый вектор. От полученного отрезка откладывается следующий вектор. Второй отрезок нужно направить в противоположную сторону. Линия, соединяющая отрезки, будет являться разностью векторов.

С векторами также можно проводить операцию умножения. Произведение длин направленных отрезков на косинус угла между ними называется скалярным. В результате вычислений получается число — скаляр. Скалярное произведение равно 0 в случае, когда отрезки пересекаются под углом 90°. Зная скалярное произведение, человек сможет найти косинус угла между построенными векторами.

Полученные в результате выполнения алгебраических операций выражения применяются для исследования перемещения тел вокруг оси вращения и изучения элементов высшей математики. Также направленные отрезки нашли широкое применение в геометрии и астрономии.

Задача о неупругом ударе

Условие.
На рельсах стоит неподвижная платформа. К ней приближается вагон со скоростью 4 м/с. и вагона – 10 и 40 тонн соответственно. Вагон ударяется о платформу, происходит автосцеп. Необходимо вычислить скорость системы “вагон-платформа” после удара.

Решение.
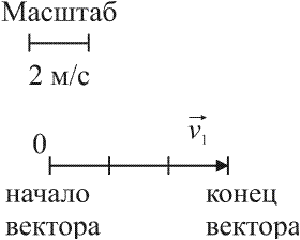
Сначала требуется ввести обозначения: скорость вагона до удара — v 1 , вагона с платформой после сцепки — v, масса вагона m 1 , платформы — m 2 . По условию задачи необходимо узнать значение скорости v.

Правила решения подобных заданий требуют схематичного изображения системы до и после взаимодействия. Ось OX разумно направить вдоль рельсов в ту сторону, куда движется вагон.

В данных условиях систему вагонов можно считать замкнутой. Это определяется тем, что внешними силами можно пренебречь. Сила тяжести и уравновешены, а трение о рельсы не учитывается.

Согласно закону сохранения импульса, их векторная сумма до взаимодействия вагона и платформы равна общему для сцепки после удара. Сначала платформа не двигалась, поэтому ее импульс был равен нулю. Перемещался только вагон, его импульс — произведение m 1 и v 1 .

Так как удар был неупругий, то есть вагон сцепился с платформой, и дальше он стали катиться вместе в ту же сторону, то импульс системы не изменил направления. Но его значение стало другим. А именно произведением суммы массы вагона с платформой и искомой скорости.

Можно записать такое равенство: m 1 * v 1 = (m 1 + m 2) * v. Оно будет верно для проекции векторов импульсов на выбранную ось. Из него легко вывести равенство, которое потребуется для вычисления искомой скорости: v = m 1 * v 1 / (m 1 + m 2).

По правилам следует перевести значения для массы из тонн в килограммы. Поэтому при подстановке их в формулу следует сначала умножить известные величины на тысячу. Простые расчеты дают число 0,75 м/с.

Ответ.
Скорость вагона с платформой равна 0,75 м/с.

Что такое векторная величина?

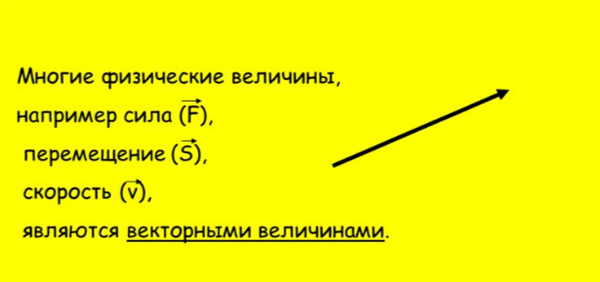
Векторная величина имеет две основные характеристики: направление и модуль. Два вектора будут одинаковыми, если их значение по модулю и направление совпадают. Для обозначения векторной величины чаще всего используют буквы, над которыми отображается стрелочка. В качестве примера векторной величины можно привести силу, скорость или ускорение.

Для того, чтобы понять сущность векторной величины, следует рассмотреть ее с геометрической точки зрения. Вектор представляет собой отрезок, имеющий направление. Длина такого отрезка соотносится со значением его модуля. Физическим примером векторной величины является смещение материальной точки, перемещающейся в пространстве. Такие параметры, как ускорение этой точки, скорость и действующие на нее силы, электромагнитного поля тоже будут отображаться векторными величинами.

Если рассматривать векторную величину независимо от направления, то такой отрезок можно измерить. Но, полученный результат будет отображать только лишь частичные характеристики величины. Для ее полного измерения следует дополнить величину другими параметрами направленного отрезка.

В векторной алгебре существует понятие нулевого вектора. Под этим понятием подразумевается точка. Что касается направления нулевого вектора, то оно считается неопределенным. Для обозначения нулевого вектора используется арифметический нуль, набранный полужирным шрифтом.

Если проанализировать все вышесказанное, то можно сделать вывод, что все направленные отрезки определяют вектора. Два отрезка будут определять один вектор только в том случае, если они являются равными. При сравнении векторов действует тоже правило, что и при сравнении скалярных величин. Равенство означает полное совпадение по всем параметрам.

И зачем нам это всё

Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например: 

• На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица. 
• Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом. 

Что такое искусственный интеллект

Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте. 

И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.

Определение положительного скаляра и его измерения

Понятие положительной скалярной величины и ее измерения позволяет сравнивать между собой однородные скаляры. Положительная скалярная величина способна принимать значения строго выше 0. Она обозначается знаком «+». Если величина может принимать значения меньше 0, то она называется отрицательной и обозначается символом «-«. Большинство скаляров могут быть только положительными. Для их расчета используют единицы измерения — фиксированного размера объекта.

Чтобы получить скалярную величину, достаточно умножить ее числовое значение на ее единицу измерения. Для структуризации и стандартизации вычислений физических параметров тела была разработана Международная система СИ. Она устанавливает единицы измерения для каждой величины. Во время проведения расчетов скалярных величин применяют алгебраические действия — сложение, вычитание, деление и умножение (отдельный подвид — возведение в степень).

Скалярные величины: характеристики и применение

Основными характеристиками скалярных величин являются:

• Величина — определяет числовое значение скаляра;
• Единица измерения — позволяет однозначно определить, в каких единицах измеряется скаляр;
• Масса — указывает на количество вещества или энергии, содержащейся в скаляре;
• Время — отражает момент или интервал времени, которое связано с скаляром;
• Плотность — обозначает количество скалярных величин на единицу объема;
• Скорость — показывает изменение скаляра в единицу времени;
• Температура — отражает степень нагретости или охлаждения скаляра.

Скалярные величины имеют широкое применение в различных областях науки и техники. Например, они используются в физике для описания физических процессов, в химии для измерения химических соединений, в математике для определения их взаимосвязей и т.д.

Скаляры также широко применяются в повседневной жизни. Например, измерение температуры с помощью термометра — это измерение скалярной величины. Оценка массы продуктов в супермаркете с помощью весов также является измерением скаляра.

Важной особенностью скалярных величин является возможность их сложения и вычитания друг из друга. Например, сложение масс двух предметов даст общую массу этих предметов

Однако нельзя умножать или делить скаляры без привязки к вектору.

Использование и понимание скалярных величин является основой для дальнейшего изучения векторных величин и их применения в различных областях науки и техники.

Как отличить скалярную величину от векторной?

Первая всегда имеет только одну характеристику. Это ее числовое значение. Большинство скалярных величин могут принимать как положительные, так и отрицательные значения. Их примерами может служить электрический заряд, работа или температура. Но есть такие скаляры, которые не могут быть отрицательными, например, длина и масса.

Векторная величина, кроме числовой величины, которая всегда берется по модулю, характеризуется еще и направлением. Поэтому она может быть изображена графически, то есть в виде стрелки, длина которой равна модулю величины, направленной в определенную сторону.

При письме каждая векторная величина обозначается знаком стрелки на буквой. Если идет речь о числовом значении, то стрелка не пишется или ее берут по модулю.

Векторные и скалярные величины

Это называется величины к измеримым (измеримым) физическим атрибутам объектов или взаимодействиям между ними, таким как силы, температура, длина, электрический заряд или многие другие переменные. В зависимости от определенных характеристик величины могут быть двух типов: скалярные и векторные.

В скалярные величины – это те, которые могут быть представлены числовой шкалой, в которой каждое конкретное значение показывает большую или меньшую степень шкалы. Например: температура, длина.

В векторные величиныВместо этого они содержат гораздо больше информации, чем может быть просто представлено на рисунке, а также требуют определенного смысла или направления в рамках данной системы отсчета. Например: скорость, сила. Для этого вектор как представление уникального чувства величины. Каждый вектор определяется четырьмя свойствами:

Примеры векторных величин

1. Масса. Вес – это величина, которая выражает силу, прилагаемую объектом к точке опоры, как следствие местного гравитационного притяжения. Он представлен векторно от центра тяжести объекта к центру Земли или объекта, создавая сила тяжести. Это вектор, потому что он имеет величину (m * g), направление (линия, идущая от центра тяжести объекта к центру Земли) и направление (к центру Земли).
2. Сила. Под силой понимается все, что может изменить положение, форму или величину движения объекта или частицы. Сила – это вектор, потому что, помимо величины (интенсивности), для описания силы необходимы направление и чувство.
3. Ускорение. Эта векторная величина выражает изменение скорости в единицу времени. У ускорения всегда есть направление и смысл, это не одно и то же – ускоряться (двигаться все быстрее и быстрее), чем тормозить. Разница выражается в изменении направления вектора ускорения.
4. Скорость. Он выражает расстояние, пройденное объектом за заданную единицу времени. Как и ускорение, скорость всегда требует направления и чувства, чтобы определить ее.
5. Торсион. Также называемый «крутящий момент», он выражает меру изменения направления вектора в сторону кривизны, поэтому он позволяет рассчитывать скорости и ритмы вращения, например, рычага. Следовательно, он заслуживает информации о векторном позиционировании.
6. Должность. Эта величина относится к местоположению частицы или объекта в пространстве-времени. Чтобы определить положение, вам нужно знать расстояние и его направление относительно оси. Например, Чили находится на некотором расстоянии от Аргентины на западе, а Сидней – на некотором расстоянии к востоку. Без адресных данных позиция не определяется полностью.
7. Электрическое напряжение. Электрическое напряжение, также известное как напряжение, представляет собой разность электрических потенциалов между двумя точками или двумя частицами. Поскольку он напрямую зависит от пути заряда между начальной и конечной точкой, то есть от потока электронов, он требует выражения векторной логики.
8. Электрическое поле. Электрические поля описывают электрические силы. Силы – векторы, поля тоже.

Что такое вектор

Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.

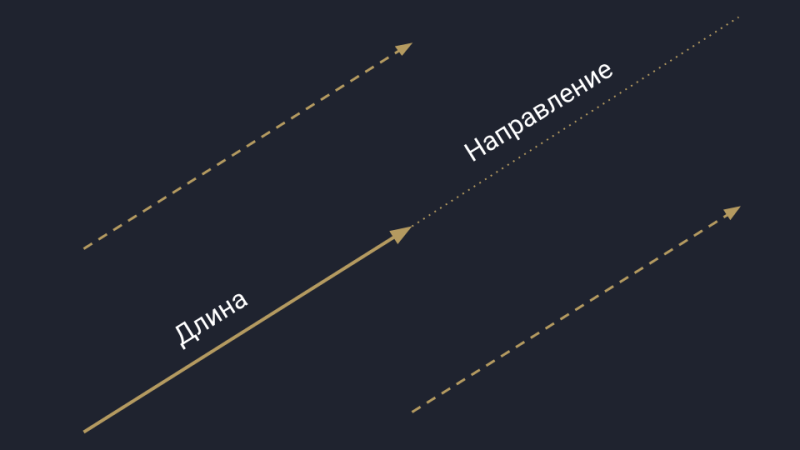Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве

У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.

Аналитическое представление вектора: данные можно перевести в числа

Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.

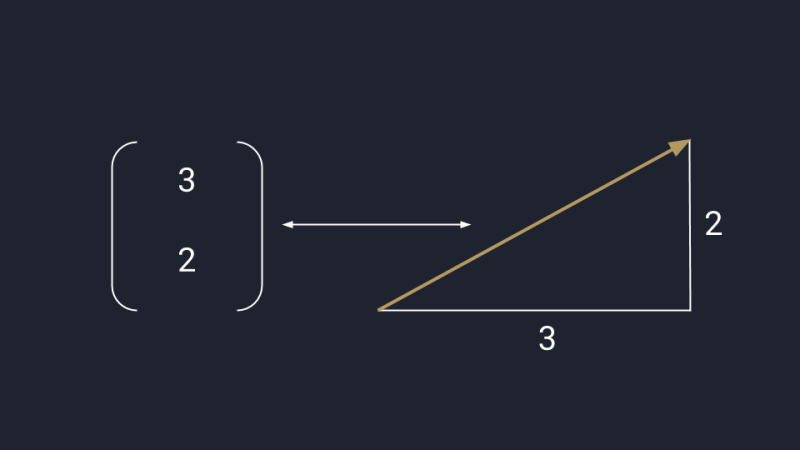Математическое представление вектора: данные можно перевести в числа или график

В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.

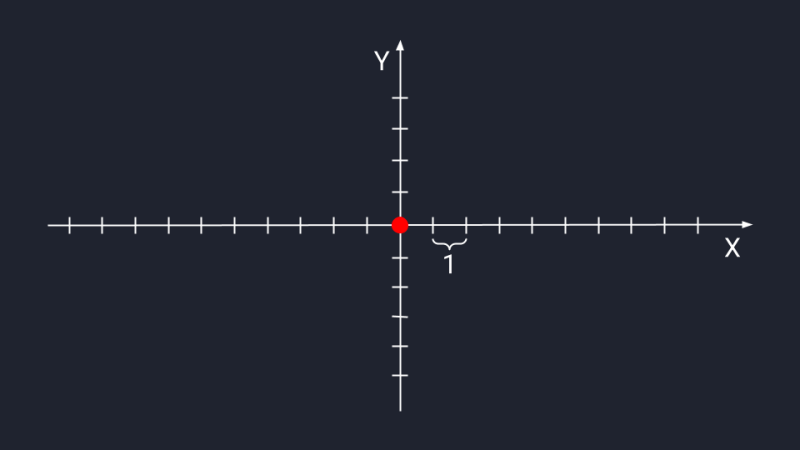Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат

Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами. 

Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.  

Какие действия чаще всего выполняются с векторами?

Сначала — сравнение. Они могут быть равными или нет. В первом случае их модули одинаковые. Но это не единственное условие. У них должны быть еще одинаковые или противоположные направления. В первом случае их следует называть равными векторами. Во втором они оказываются противоположными. Если не выполняется хотя бы одно из указанных условий, то векторы не равны.

Потом идет сложение. Его можно сделать по двум правилам: треугольника или параллелограмма. Первое предписывает откладывать сначала один вектор, потом от его конца второй. Результатом сложения будет тот, который нужно провести от начала первого к концу второго.

Правило параллелограмма можно использовать, когда нужно сложить векторные величины в физике. В отличие от первого правила, здесь их следует откладывать от одной точки. Потом достроить их до параллелограмма. Результатом действия следует считать диагональ параллелограмма, проведенную из той же точки.

Если векторная величина вычитается из другой, то они снова откладываются из одной точки. Только результатом будет вектор, который совпадает с тем, что отложен от конца второго к концу первого.

Сравнительная таблица

Основа для сравнения	Скалярная величина	Количество векторов
Смысл	Любая физическая величина, которая не включает в себя направление, называется скалярной величиной.	Количество векторов равно единице, которая имеет величину и направление.
Количества	Одномерные величины	Многомерные величины
+ Изменить	Это изменяется с изменением их величины.	Это изменяется с изменением их направления или величины или обоих.
операции	Следуйте обычным правилам алгебры.	Следуйте правилам векторной алгебры.
Сравнение двух величин	просто	Сложный
разделение	Скаляр может делить еще один скаляр.	Два вектора никогда не могут делиться.

Вектор и скаляр в формулах

В учебниках по физике часто встречаются формулы, в которых есть стрелочка сверху. Вспомните второй закон Ньютона. Сила (“F” со стрелочкой сверху) равна произведению массы (“m”) и ускорения (“a” со стрелочкой сверху). Как говорилось выше, сила и ускорение являются величинами векторными, а вот масса – скалярной.

К сожалению, не во всех изданиях есть обозначение этих величин. Наверное, сделано это для упрощения, чтобы школьников не вводить в заблуждение. Лучше всего покупать те книги и справочники, в которых обозначены векторы в формулах.

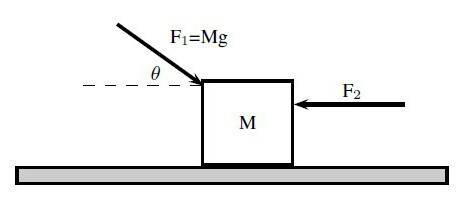
То, какая величина является векторной, покажет иллюстрация

Рекомендуется обращать внимание на картинки и схемы на уроках физики. Векторные величины имеют направление

Куда направлена Конечно же, вниз. Значит, стрелочка будет показана в том же направлении.

В технических вузах изучают физику углубленно. В рамках многих дисциплин преподаватели рассказывают о том, какие величины являются скалярными и векторными. Такие знания требуются в сферах: строительство, транспорт, естественные науки.

Величины называются скалярными (скалярами), если они после выбора единицы измерения полностью характеризуются одним числом. Примерами скалярных величин являются угол, поверхность, объем, масса, плотность, электрический заряд, сопротивление, температура.

Следует различать два типа скалярных величин: чистые скаляры и псевдоскаляры.

3.1.1. Чистые скаляры.

Чистые скаляры полностью определяются одним числом, не зависящим от выбора осей отсчета. Примером чистых скаляров могут служить температура и масса.

3.1.2. Псевдоскаляры.

Как и чистые скаляры, псевдоскаляры определяются с помощью одного числа, абсолютная величина которого не зависит от выбора осей отсчета. Однако знак этого числа зависит от выбора положительных направлений на осях координат.

Рассмотрим, например, прямоугольный параллелепипед, проекции ребер которого на прямоугольные оси координат соответственно равны Объем этого параллелепипеда определяется с помощью определителя

абсолютная величина которого не зависит от выбора прямоугольных осей координат. Однако, если переменить положительное направление на одной из осей координат, то определитель изменит знак. Объем – это псевдоскаляр. Псевдоскалярами являются также угол, площадь, поверхность. Ниже (п. 5.1.8) мы увидим, что псевдоскаляр представляет собой в действительности тензор особого рода.

3.1.3. Ось.

Ось – это бесконечная прямая, на которой выбрано положительное направление. Пусть такая прямая, а направление от

считается положительным. Рассмотрим отрезок на этой прямой и положим, что число, измеряющее длину равно а (рис. 3.1). Тогда алгебраическая длина отрезка равна а, алгебраическая длина отрезка равна – а.

Если взять несколько параллельных прямых, то, определив положительное направление на одной из них, мы тем самым определяем его на остальных. Иначе обстоит дело, если прямые не параллельны; тогда нужно специально уславливаться относительно выбора положительного направления для каждой прямой.

3.1.4. Направление вращения.

Пусть ось. Вращение относительно оси назовем положительным или прямым, если оно осуществляется для наблюдателя, стоящего вдоль положительного направления оси, справа и налево (рис. 3.2). В противном случае оно называется отрицательным или обратным.

3.1.5. Прямые и обратные трехгранники.

Пусть некоторый трехгранник (прямоугольный или непрямоугольный). Положительные направления выбраны на осях соответственно от О к х, от О к у и от О к z.

Определение скалярного количества

Термин «скалярная величина» определяется как величина, имеющая только один элемент числового поля, связанный с единицей измерения, например градусами или метрами. Это величина, которая демонстрирует только величину или размер, то есть она определяется числовым значением вместе с единицей измерения. Например, скорость автомобиля, температура тела, расстояние между двумя точками и т. Д.

Правила обычной алгебры могут применяться для объединения скалярных величин, так что скаляры можно складывать, вычитать или умножать так же, как числа. Однако работа скаляра возможна только для величин с одинаковыми единицами измерения.