Разница между сочетанием и размещением

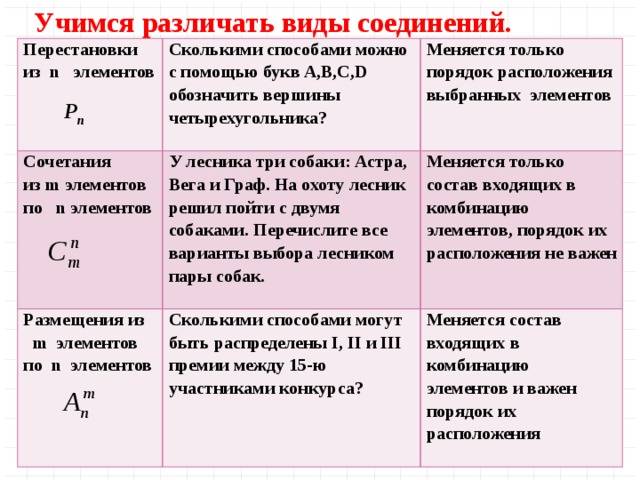
Перестановка

Перестановка — это способ последовательно расположить составляющие множества. Например, 123, 312 и 213 — это перестановки трёх чисел: 1, 2 и 3.

Чтобы найти общее количество возможных перестановок, используют две формулы: для случаев с повторяющимися компонентами и без них. Давайте рассмотрим оба.

Перестановка без повторяющихся элементов

Если во множестве ни один элемент не повторяется, то используется следующая формула:

Пример: сколько перестановок символов можно составить из шести букв — q, w, e, r, t, y?

Решение: чтобы найти количество перестановок, нам нужно посчитать факториал числа 6 — то есть общего количества букв в наборе. Подставляем в формулу:

Перестановка с повторяющимися элементами

Если хотя бы один элемент во множестве повторяется, то используется следующая формула:

Формула выглядит довольно негуманно, поэтому объясним, в чём здесь логика. Сначала мы находим, сколько перестановок было бы, если бы все компоненты множества были разными. Потом мы делим это число на то, сколько раз можно переставить повторяющиеся элементы между собой. Это нужно, чтобы не считать одинаковые перестановки несколько раз. Дальше мы посмотрим на пример, чтобы лучше разобраться.

Пример. Допустим, у нас есть набор из восьми букв: p, a, s, s, w, o, r, d. Сколько всего перестановок символов можно составить из этих букв?

Решение. Видим, что буква s в этом наборе повторяется дважды. Значит, n = 8 и n₁ = 2. Подставляем эти значения в формулу и получаем:

Комбинирования. Расположения. Перестановки

Перестановками именуют конфигурации, которые состоят из одних и тех же n разных элементов и выделяющиеся только порядком их расположения. Число всех потенциальных перестановок

Комбинаторика 3. Число сочетаний

https://youtube.com/watch?v=FR_1_Py0gro

Где

).

Рассмотрим пример: сколько трехзначных чисел можно составить из цифр 1,2,3, если каждая цифра входит в изображение числа лишь единожды?

.
Или такой пример.

Порядок выступления семи участников на студенческой конференции определяется жребием. Сколько разных вариантов жеребьевки при этом возможно?

Решение: любой вариант жеребьевки отличается только порядком участников, другими словами считается перестановкой из 7 элементов. Их число находится

Комбинаторика, факториал, перестановка, размещение, сочетание

Пример. К кассе за получением денег подошли одновременно 4 человека.

Сколькими способами они могут выстроиться в очередь?

Решение: очередь состоит из 4 разных лиц, благодаря этому в каждом способе составления очереди принимается во внимание порядок их расположения. Аналогичным образом, имеют место перестановки из 4-ех человек, их число равно. Расположениями именуют конфигурации, которые составлены из n разных элементов по m элементов, которые выделяются либо их порядком, либо составом элементов.

Расположениями именуют конфигурации, которые составлены из n разных элементов по m элементов, которые выделяются либо их порядком, либо составом элементов.

Число всех потенциальных локаций рассчитывается

Пример: сколько можно составить сигналов из 6 флажков разного цвета, взятых по два?

Комбинаторика: размещения, перестановки, сочетания

Пример: расписание одного дня состоит из пяти уроков.

Определить число вариантов расписания при подборе из 11 дисциплин.Решение: любой вариант расписания представляет набор 5 дисциплин из 11, выделяющийся от иных вариантов, как составом дисциплин, так и порядком их движения, другими словами считается расположением из 11 элементов по 5. Число вариантов расписания находят по формуле

Комбинированиями именуют конфигурации, которые составлены из n разных элементов по m элементов, которые выделяются хотя бы одним элементом.

Число сочетаний

Пример: сколькими способами можно подобрать 2 детали из ящика, содержащего 10 деталей?

Пример: в шахматном турнире принимают участие 16 человек.

Сколько партий должно быть сыграно в турнире, если между любыми 2-мя участниками должна быть сыграна одна партия?Решение: каждая партия играется 2-мя участниками из 16 и отличается только составом пар участников, другими словами собой представляет комбинирование из 16 элементов по два

Пример: есть 6 штаммов бактерий.

Для определения скорости их роста нужно подобрать три штамма.

Сколькими способами можно это сделать?Решение: способы отбора считаются разными, если каждый отобранный штамм отличается хотя бы одним элементом.

Это число

Другими словами есть 20 вариантов.

Необходимо выделить, что числа локаций, перестановок и сочетаний связаны равенством

При решении задач комбинаторики применяют такие правила.

Правило суммы: если некоторый объект A может быть подобран из совокупности объектов m способами, а другой объект В может быть подобран n способами, то подобрать либо А, либо В можно

способами.Правило произведения: если объект А можно подобрать из совокупности объектов m способами и после любого подобного выбора объект В можно подобрать n способами, то пара объектов (А,В) в указанном порядке может быть подобрана

способами.

Пример: в студенческой группе 14 девушек и 6 юношей. Сколькими способами можно подобрать, для исполнения самых многообразных заданий, 2-ух студентов одного пола?

Решение: по правилу перемножения 2-ух девушек можно подобрать

способами, а 2-ух юношей

способами. Необходимо выбирать 2-ух студентов одного пола: 2-ух девушек или 2-ух юношей.

Согласно правилу сложения этих методов выбора будет 182 + 30 = 212.Контрольные вопросы

2. Какие вершины графа можно назвать соседними?

3. Реально ли нарисовать граф с нечетным числом нечетных вершин?
4. Чем определяется полный граф?

5. Что именуют перестановками, расположениями, комбинированиями?
6. Выразить правила суммы и произведения.

Комбинаторика: правило размещения без повторений

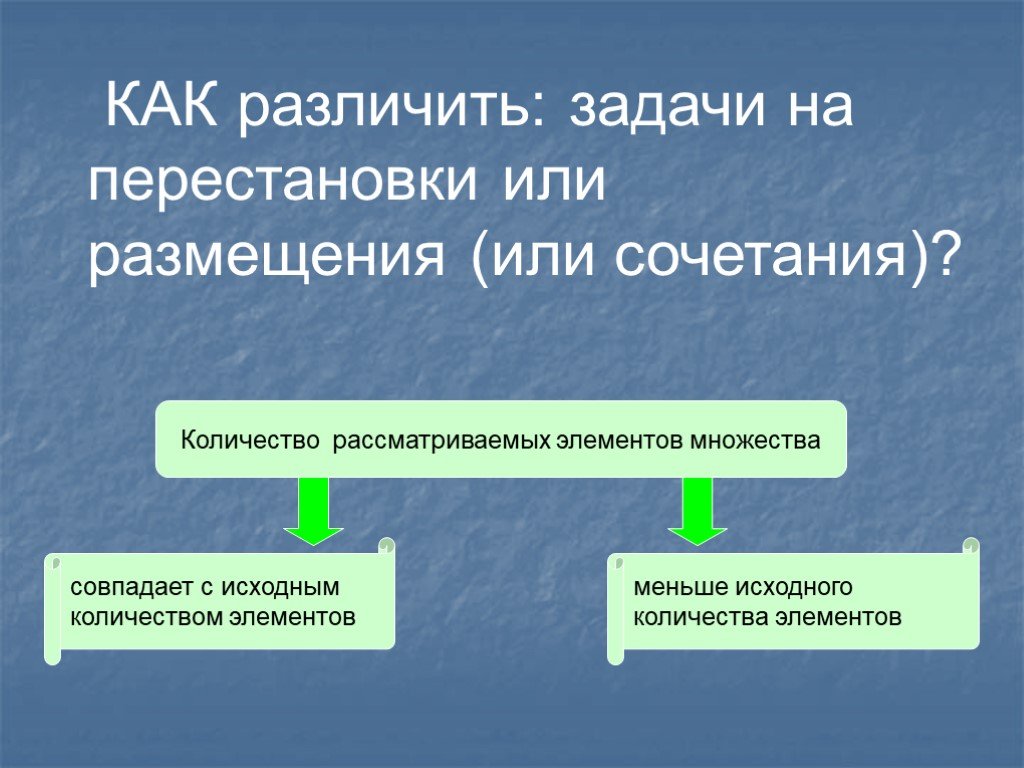
Подмножество, выбираемое из данного множества предметов, называют выборкой. Выборки бывают упорядоченные и неупорядоченные. Для упорядоченной выборки существенен порядок элементов. Иначе говоря, меняя порядок элементов, мы получаем другие выборки. Составим, например, из цифр 1, 2, 3, 4, 5 трехзначные числа: 123, 431, 524 и т.д. Это упорядоченные трехэлементные выборки, отличающиеся составом или порядком элементов.

Размещениями из $n$ элементов по $m$ элементов ($m$≤$n$) называют упорядоченные $m$-элементные выборки из данных $n$ элементов.

Формула размещения без повторений в комбинаторике $n$ по $m$ элементов имеет вид: $A_{n}^{m} =\frac{n!}{\left(n-m\right)!} $.

Размещения

В самом названии этого термина присутствует корень, позволяющий понять его суть. Размещение – тоже подмножество, выбранное из первоначального множества. Но здесь уже существенное значение имеет место расположения элемента в комбинации. То есть если сочетания могут различаться только составом объектов, то размещения разнятся и составом, и порядком следования элементов.

Получается, что количество размещений всегда превосходит число сочетаний, при условии выборки из одного и того же множества.

Это легко проследить, если сделать выборку трех элементов из множества, состоящего всего из 4 объектов (от 1-го до 4-х).

Сочетаний здесь будет всего 4 (это легко проверить и по приведенной выше формуле):

123, 234, 134, 241

Размещений же окажется гораздо больше:

123, 132, 321, 312, 231, 213, 234, 243, 324, 342 и т.д.

Существует формула, позволяющая подсчитать возможное количество размещений в представленном множестве:

N!/(N – К)!

Для нашего примера посчитаем количество потенциальных размещений:

4!/(4-3)! = 24

Получается, что для состоящего из 4-х элементов множества существует 4 сочетания и целых 24 размещения.

Для тех, кто увлекается спортивными ставками, эти знания могут пригодится для того, чтобы рассчитать шансы на выигрыш.

Например, в турнире участвует 6 команд. Необходимо определить количество возможных комбинаций троек призеров кубка.

Обозначим названия команд буквами: А, Б, В, Г, Д, Е.

Сначала определим команду, которая станет золотым призером чемпионата. Таких вариантов, очевидно, 6: А, Б, В, Г, Д, Е.

Затем выбираем один из вариантов (пусть это будет комбинация, в которой золото принадлежит команде А), и определяем для него потенциального серебряного призера. Таких комбинаций уже окажется всего 5, так как одна команда уже записана на 1-м месте: АБ, АВ, АГ, АД, АЕ.

Такую пятерку вариаций можно сформировать для каждой из команд. То есть всего претендентов на серебро оказывается 30 (5*6).

Для каждой двойки первых призеров (чемпион-серебряный призер) можно составить только 4 комбинации с бронзовым призером. Первые два места уже распределены, так что остается 4 команды (6-2). Подберем комбинации для варианта АБ: АБВ, АБГ, АБД, АБЕ.

Мы уже подсчитали выше количество возможных комбинаций для первых двух мест – их оказалось 30. Теперь это число умножаем на 4 – получаем 120.

Выходит, что если в турнире участвует 6 команд, вариантов их размещения по первым трем местам может быть целых 120. Угадать призеров не так просто.

Сочетания

Выбирая размещение, мы должны были выбрать из множества несколько объектов и упорядочить их. В частности, мы выбирали три команды из шести и указывали, какая из них будет первой, какая второй, а какая третьей. Поэтому размещения «Локомотив, Зенит, Краснодар» и «Локомотив, Краснодар, Зенит» отличались друг от друга.

Однако порою этот порядок не имеет значения. Так, существует известная лотерея, где предлагается угадать 7 чисел из 49, которые выпадут во время розыгрыша из барабана. При этом порядок их выпадения не играет никакой роли. Игрок, выбирая эти 7 чисел, с точки зрения математики формирует сочетание из 49 по 7.

Количество возможных сочетаний из n по k обозначается буквой С:

Для вычисления количеств сочетаний из n по k сначала найдем количество аналогичных размещений. Оно вычисляется по формуле:

Однако ясно, что, как и в случае с перестановками с повторениями, некоторые сочетания мы посчитали несколько раз. Вернемся к примеру с командами. Если мы выбрали команды Л (Локомотив) , З (Зенит) и К (Краснодар), то мы можем составить ровно 3! = 6 размещений из них:

ЛЗК

ЛКЗ

ЗЛК

ЗКЛ

КЛЗ

КЗЛ

Однако все они соответствуют только одному сочетании – ЛКЗ. Таким образом, считая количество размещений, мы посчитали каждое сочетание не один, а 3! раз. Поэтому для нахождения количества сочетаний в комбинаторике надо поделить число размещений на число перестановок k элементов:

Эта формула связывает важнейшие понятия комбинаторики – перестановки, сочетания и размещения. Подставим в неё формулы для размещений и перестановок и получим:

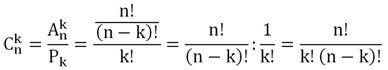
Пример. Сколько троек призеров турнира можно составить, выбирая три футбольные команды из шести?

Решение. Посчитаем число сочетаний из 6 по 3:

Ответ: 20

Пример. Сколько комбинаций чисел может составить игрок, играющий в лотереи «5 из 36», «6 из 45», «7 из 49»?

Решение. В каждом из этих случаев игрок выбирает сочетание нескольких чисел. Посчитаем их число:

Ответ: 376992; 8145060; 85900584

Пример. На плоскости отмечены 8 точек, причем никакие три из них не лежат на одной прямой. Сколько различных прямых можно провести через них? Сколько треугольников и четырехугольников можно построить с вершинами в этих точках?

Решение. Для того чтобы провести прямую, достаточно выбрать любые 2 точки из 8. Общее количество прямых будет равно числу сочетаний из 8 по 2:

Заметим принципиальную важность того условия, что никакие три точки не лежат на одной прямой. Оно гарантирует, что при выборе двух различных точек мы будем получать различные прямые

Если бы, например, точки АВС лежали бы на одной прямой, то при выборе сочетаний АВ, ВС и АС мы получали бы одну и ту же прямую:

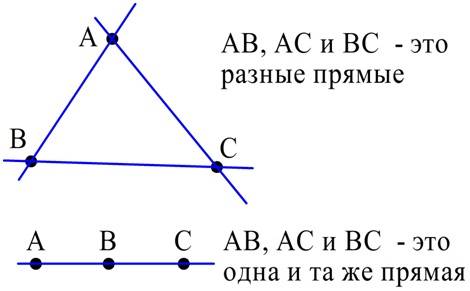
Это же условие гарантирует, что, выбрав любые 3 и 8 точек, мы сможем построить треугольник с вершинами в этих точках, а выбрав 4 точки, получим четырехугольник. Поэтому для подсчета количества треугольников и четырехугольников следует искать число сочетаний по 3 и 4:

Ответ: 28 прямых, 56 треугольников и 70 четырехугольников.

Пример. В одной урне находится 10 различных шаров с номерами от 0 до 9, а в другой – 8 различных шаров с первыми восемью буквами алфавита. По условиям лотереи ведущий вытаскивает из первой урны два шара с числами, а из второй – три шара с буквами. Для победы в лотерее надо угадать выпавшие шары. Сколько комбинаций шаров может выпасть в игре?

Решение. Посчитаем отдельно, сколькими способами можно выбрать 2 шара с цифрами из 10 и 3 шара с буквами из 8:

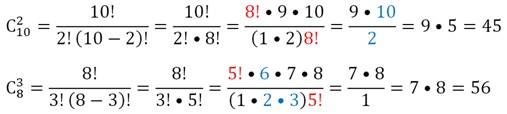
По правилу умножения мы должны перемножить эти числа, чтобы найти общее количество возможных вариантов:

56•45 = 2520

Ответ: 2520

Заметим, что выбирая, например, сочетание из 49 по 7, мы одновременно выбираем и сочетание из 49 по 49 – 7 = 42. Действительно, игрок, обводящий в кружок в лотерейном билете свои 7 счастливых чисел, одновременно и определяет остальные 42 числа, какие числа он НЕ считает счастливыми. Для наглядности запишем число сочетаний в обоих случаях:

Получили одну и ту же дробь, в которой отличается лишь последовательность множителей в знаменателе. Можно показать, что и в общем случае число сочетаний из n по k совпадает с количеством сочетаний из n по (n– k):

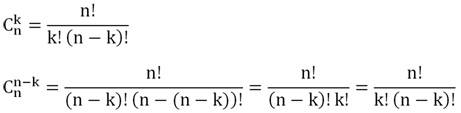
Лекция 2. Перестановки, сочетания, размещения

Пусть имеется n различных объектов. Будем переставлять их всеми различными способами ( число и состав объектов остается неизменным, меняется только порядок). Получившиеся комбинации называются перестановками, а их число равно

Символ называется факториалом и обозначает произведение всех целых чисел от 1 до n. По определению считают, что , . Факториал растет очень быстро (недаром он обозначается восклицательным знаком !), например:

Пример: Сколько способов рассадить шестерых гостей на шести стульях?

Решение.

Перестановки с повторениями

Задача1. Сколько различных “слов” можно получить, переставляя буквы слова “передача” ?

В этом слове буквы “е” и “а” встречаются два раза, остальные по одному разу. Речь идет о перестановке с повторением состава (2,2,1,1,1,1) длины n равно 2+2+1+1+1+1=8. Количество таких равно

Сочетания

В сочетанием из по называется набор элементов, выбранных из данных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.

Пусть имеется различных объектов

Чтобы найти число сочетаний из объектов по , будем выбирать комбинации из объектов всеми возможными способами, при этом будем обращать внимание на разный состав комбинаций, но не порядок (он тут не важен). Например, есть три объекта {1,2,3}, составляем сочетания по 2 объекта в каждом

Тогда {1,2} и {2,1} – это одно и то же сочетание (так как комбинации отличаются лишь порядком). А всего различных сочетаний из 3 объектов по 2 будет три: {1,2}, {1,3}, {2,3}.

На картинке наглядно проиллюстрировано получение всех возможных сочетаний из 4 различных объектов по 2

Формула для нахождения числа сочетаний имеет вид

Задача2. Сколько существует способов назначить двоих дежурных из семи человек?

Решение.

Сочетания с повторениями – это комбинации, составленные из различных элементов по элементов, среди которых встречаются одинаковые. Комбинации отличаются хотя бы одним элементом. Формула для вычисления числа сочетаний с повторениями:

Задача3. В кондитерском магазине продается 4 сорта пирожных: наполеон, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Решение.

Пусть имеется различных объектов.

Будем выбирать из них объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из объектов по , а их число равно

Чтобы найти размещения, надо взять все возможные сочетания, а потом в каждом еще поменять порядок всеми возможными способами (то есть фактически сделать еще перестановки). Поэтому число размещений еще выражается через число перестановок и сочетаний так:

Задача4. В группе туристов 9 человек. Сколько существует способов распределить между ними обязанности командира, его заместителя и кашевара?

Решение.

Если n различных элементов могут повториться m раз, оказавшись соответственно на m местах, то число размещений с повторениями вычисляется по формуле

Задача5. Сколько трехзначных чисел можно записать, используя любые цифры из набора 1,2,3,4,5?

Решение.

Основные элементы комбинаторики

Размещения

Это любое упорядоченное подмножество из элементов множества .
(Порядок важен).

Типичная смысловая нагрузка: сколькими способами можно выбрать объектов (из объектов) и в каждой переставить их местами (либо распределить между ними какие-нибудь уникальные атрибуты)?

Перестановки

Если , то эти размещения называются перестановками.

Типичная смысловая нагрузка: сколькими способами можно переставить nобъектов?

Сочетания

Это любое подмножество из элементов, которые принадлежат множеству, состоящему из различных элементов.
(Порядок не важен)

Типичная смысловая нагрузка: сколькими способами можно выбрать объектов из ?

Соединения с повторениями

1) Перестановки с повторениями

2) Сочетания с повторениями:

3) Размещения с повторениями:

Число размещений – это …

число способов переставить объектовчисло способов выбрать объектов из число способов выбрать объектов из и в каждой выборке переставить их местами

Формула для нахождения числа сочетаний:

Сколько существует способов рассадить четырех гостей на четыре стула?

81624120

В оперном театре 10 певцов и 8 певиц. В постановке участвуют три мужских голоса и два женских. Сколько существует способов распределить их роли между актерами?

1880336040320

В оперном театре 10 певцов и 8 певиц. В постановке участвуют три мужских голоса и два женских. Сколько существует способов выбрать актеров для постановки?

1880336040320

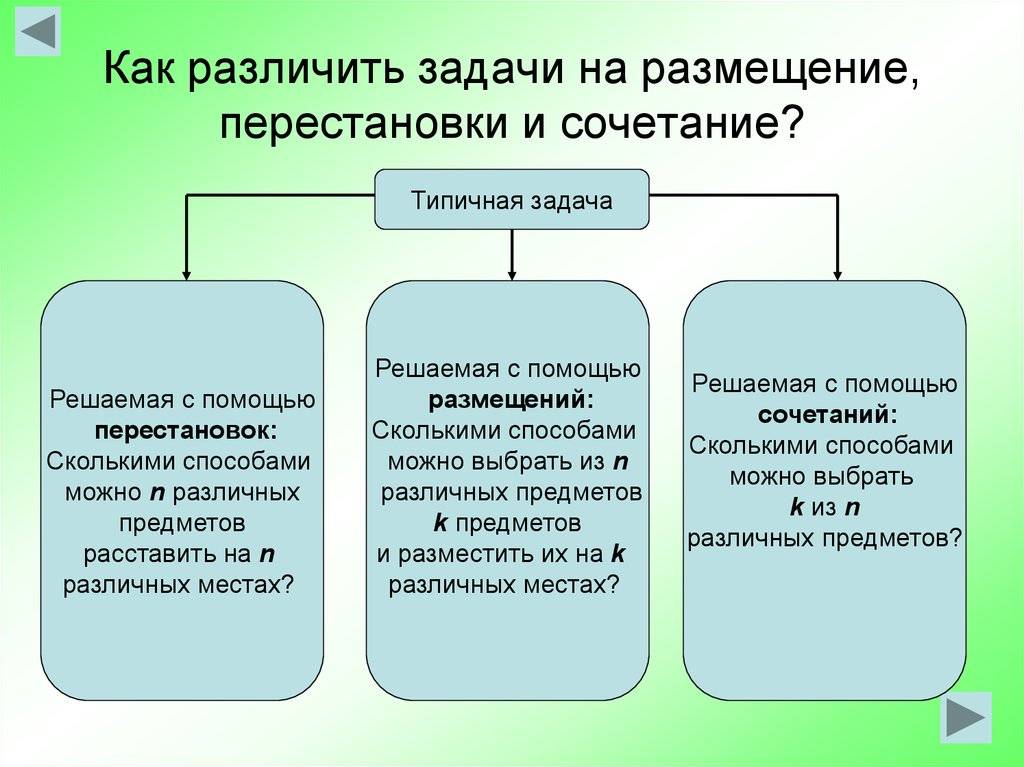
Ключевые различия между перестановкой и комбинацией

Различия между перестановкой и комбинацией четко показаны по следующим основаниям:

1. Термин «перестановка» относится к нескольким способам упорядочения набора объектов в последовательном порядке. Комбинация предполагает несколько способов выбора предметов из большого пула объектов, так что их порядок не имеет значения.
2. Основное различие между этими двумя математическими понятиями – это порядок, размещение и положение, т. Е. В вышеупомянутых характеристиках перестановки имеет значение, что не имеет значения в случае комбинации.
3. Перестановка обозначает несколько способов упорядочения вещей, людей, цифр, алфавитов, цветов и т. Д. С другой стороны, комбинация указывает на разные способы выбора пунктов меню, еды, одежды, предметов и т. Д.
4. Перестановка – не что иное, как упорядоченная комбинация, в то время как Комбинация подразумевает неупорядоченные множества или пары значений в пределах определенных критериев.
5. Многие перестановки могут быть получены из одной комбинации. И наоборот, только одна комбинация может быть получена из одной перестановки.
6. Ответы на перестановки Сколько разных аранжировок можно создать из данного набора объектов? В отличие от комбинации, которая объясняет, сколько разных групп можно выбрать из большой группы объектов?

Правило умножения

Правило умножения используется в том случае, если у нас есть два множества, и мы составляем всевозможные пары из элементов этих множеств. Например, если взять множество, состоящее из 5-ти яблок и множество, состоящее из 7-ми груш и составить всевозможные пары из этих фруктов, то мы получим всевозможных пар.

Действительно. Возьмем первое яблоко. Мы можем положить к нему любую из семи груш, то есть получаем 7 пар. Возьмем второе яблоко, и к нему мы также можем положить любую из 7-ми груш, получаем ещё 7 пар.  И так далее. Всего получается пар.

Правило умножения легко понять, если попытаться ответить, например, на такой вопрос: “сколько существует двузначных чисел?”

Пусть двузначное чиcло имеет вид , где – число десятков, – число единиц. При этом цифра может принимать значения от 1 до 9 ( цифра 0 не может стоять на первом месте, так как в этом случаем мы получим однозначное число), цифра   может принимать значения от 0 до 9.

Пусть , и у нас есть 10 вариантов цифр, которые могут стоять на втором месте. Тогда мы имеем 10 двузначных чисел, содержащих 1 десяток.

Затем мы берем и так же получаем 10 двузначных чисел, у которых теперь уже 2 десятка.

И так далее.

Так как цифра может принимать 9 различных значений, то получаем двузначных чисел.

Зная, что на первом месте может стоять 9 различных цифр, а на втором  – 10, мы получаем комбинаций этих цифр, то есть все возможные двузначные числа

Здесь важно понимать, что любая цифра, стоящая на первом месте, может сочетаться с любой цифрой, стоящей на втором месте

В общем случае правило умножения звучит так:

Если элемент A можно выбрать n способами, и при любом выборе A элемент B можно выбрать m способами, то пару (A, B) можно выбрать n·m способами. Это правило распространяется на любое число независимо выбираемых элементов.

Если мы хотим ответить на вопрос, сколько существует трехзначных чисел, мы заметим, что в трехзначном числе первая цифра может принимать 9 значений, вторая   – 10, и третья – 10 значений. И мы получаем трехзначных чисел.

Размещения

Размещение очень похоже на перестановку, с одной лишь разницей: у нас обычно “не хватает” позиций (коробочек) для размещения всех элементов (кубиков).

Обозначается размещение n из k так:

\

При k = n (то есть когда число “коробочек” равно числу “кубиков”) количество размещений равно количеству перестановок порядка n.

\

Возьмем задачу из примера: Сколько трехзначных чисел можно создать из цифр от 1 до 5?

Если мы по аналогии с перестановками попробуем по шагам считать, то увидим, что мы остановились после заполения третьей (последней) “коробочки”:

5⋅ 4⋅ 3 = 60

А множители 2 и 1 отсуствуют: 5⋅ 4⋅ 3⋅ 2⋅ 1. То есть, число в 2! раз меньше.

Мы можем записать так: 

\

а в общем виде так:

\

Размещение с повторением

Существует вариант, когда мы можем повторно использовать один и тот же элемент, независимо от того, использовали мы его до этого, или нет. В случае с кубиками и коробочками это будет выглядеть так: у нас есть не по одному кубику с каждым номером, а неограниченное число кубиков с каждым из чисел. Это называется размещение n из k с повторением и обозначается:

\

Начнем заполнять “коробочки”.

У нас есть пять кубиков с цифрами: 1,2,3,4,5.

У нас есть пять, пока еще свободных, позиций под их размещение (пусть это будут пустые коробочки): ▢▢▢▢▢.

Положим, в первую мы кладем номер 4.

Значит у нас осталось четыре свободных “коробочки”: 4▢▢▢▢.

Начинаем заполнять вторую коробочку. Их у нас четыре, как я уже сказал. Но кубиков у нас, в отличии от размещения без повторения осталось всё равно пять. Значит у нас на каждый вариант заполения первой коробочки приходится пять вариантов заполения второй.

Соотвественно две первые коробочки мы можем заполнить 5⋅ 5 = 25 способами (а не 5⋅ 4 = 20, как в случае без повторения).

Повторяя рассуждения мы вычислим, что три коробочки мы можем заполнить 5⋅ 5⋅ 5 = 125 способами.

В общем случае число размещений равно числу элементов (кубиков) в степени числа возможных позиций для размещения (коробочек).

\

Размещения

      Рассмотрим следующую задачу.

      Задача.   9   карточек пронумерованы числами   1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 .   Из этих карточек четыре наугад взятых карточки выкладываем в ряд. Сколько при этом можно получить различных четырехзначных чисел?

      Решение.Сначала слева направо пронумеруем места в ряду, куда выкладываем карточки: первое место, второе, третье, четвертое.

      На первое место можно положить одну из   9   карточек. Для этого есть   9   способов. В каждом из этих   9   способов на второе место можно положить одну из оставшихся   8   карточек. Таким образом, существует

способа, чтобы положить карточки на первое и второе места. В каждом из этих   72   способов на третье место можно положить одну из оставшихся   7   карточек. Следовательно, существует

способа, чтобы положить карточки на первое, второе и третье места. В каждом из этих   504   способов на четвертое место можно положить одну из оставшихся   6   карточек. Отсюда вытекает, что существует

различных способа, чтобы выложить в ряд   4   карточки из набора, состоящего из   9   пронумерованных карточек. Таким образом, при выкладывании карточек можно получить   3024   различных четырехзначных числа.

      Ответ:   3024.

      При решении задачи мы провели подсчет числа способов раскладывания карточек, который является частным случаем общего метода подсчета числа размещений и заключается в следующем.

      Определение 1. Рассмотрим множество, содержащее   n   элементов, и все его , содержащие   k   элементов. Каждое из этих подмножеств называют размещением из   n   элементов по   k   элементов.

      Если обозначить символом  число размещений из   n   элементов по   k   элементов, то будет справедлива формула:

(1)

      В соответствии с , формулу (1) можно также записать в виде:

      В задаче множеством из   n   элементов является исходный набор из   9   пронумерованных карточек, а упорядоченным подмножеством из   k   элементов –   4   карточки, выложенные в ряд.

      Таким образом, при решении задачи мы на частном примере подсчитали, чему равно число размещений из   9   элементов по   4   элемента, т.е. число

      В соответствии с формулой (1),

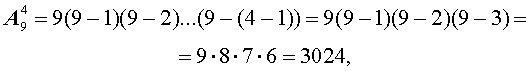
что и было получено в задаче.

      Замечание 1. Введенные в данном разделе размещения также называют размещениями без повторений.

      Замечание 2. Из формул для числа перестановок и числа размещений вытекает формула

смысл которой заключается в следующем.

      Утверждение. Размещение из   n   элементов по   n   элементов является перестановкой из   n   элементов.