Применение в естественных науках
В естественных науках размер и геометрия объектов играют важную роль при изучении различных процессов и явлений. Шар и сфера являются одной из основных форм в геометрии, которая находит широкое применение в физике, астрономии, географии и других научных дисциплинах.
Форма шара и сферы является наиболее симметричной и простой. В естественных науках эта форма используется для описания и анализа объектов, у которых поверхность одинакова во всех точках. Радиус сферы определяет размер объекта, а объем шара позволяет рассчитать его объем.
В физике шар и сфера используются для моделирования различных физических систем. Например, в механике они используются для описания движения тел, в электродинамике — для анализа распределения электрического поля, а в оптике — для описания поверхности сферических линз.
В астрономии шары и сферы используются для моделирования и изучения планет, звезд, галактик и других космических объектов. Отличительной чертой астрономических тел является их сферическая форма и равномерность распределения массы по поверхности.
В географии шар и сфера применяются для моделирования Земли и других планет. Различные географические параметры, такие как форма планеты, радиус, поверхностная температура и климат, могут быть описаны с помощью шара и сферы.
Шар — используется, например, в молекулярной биологии
Шар — это геометрическая фигура, которая имеет форму сферы. Сфера — это трехмерное тело, у которого все точки находятся на одинаковом расстоянии от центра. Шар и сфера часто используются в различных областях науки и техники, включая молекулярную биологию.
В молекулярной биологии шар обычно используется для моделирования и изучения свойств различных молекул, таких как белки, ДНК и РНК. Шары могут представлять атомы или группы атомов в молекуле, помогая исследователям понять и предсказать их взаимодействия и структуру.
Шары в молекулярной биологии имеют определенные размеры и цвета, чтобы позволить исследователям лучше визуализировать и анализировать сложные молекулярные структуры. Они часто помечаются разными цветами, чтобы показать разные типы атомов, например, кислород и водород.
Кроме того, шары могут быть использованы для создания моделей оболочек вокруг молекул или организмов. Эти оболочки называются поверхностями, и они имеют свои размеры и формы, которые могут быть анализированы и использованы для проведения различных исследований.
Шары также позволяют исследователям оценить объем молекулы или организма. Путем измерения и анализа размеров шара, можно получить информацию о размере и объеме молекулы, что является важным для понимания ее функций и свойств.
Итак, шар как геометрическая фигура используется в молекулярной биологии для моделирования и изучения молекул, а также анализа и визуализации их структуры и свойств. Он играет важную роль в понимании молекулярных процессов и помогает исследователям достичь новых открытий и прорывов в науке.
Сфера — обозначает пространство вокруг некоторого объекта
Сфера — геометрическая форма, которая описывается как множество точек, лежащих на одинаковом расстоянии от данной оси. Она представляет собой трехмерную фигуру, которая не имеет углов и ребер, а состоит только из поверхности.
Основное отличие сферы от других геометрических фигур, таких как шар, заключается в том, что шар — это объемная фигура, включающая в себя все точки, лежащие внутри сферы. То есть шар — это сфера вместе с ее внутренним пространством.
Радиус сферы — это расстояние от оси до любой точки на ее поверхности. Размер сферы определяется диаметром, который равен удвоенному радиусу.
Поверхность сферы имеет особые свойства: любая плоскость, проходящая через центр сферы, будет разделять ее на две равные полусферы. Площадь поверхности сферы вычисляется по формуле S = 4πr^2, где r — радиус сферы.
Сфера является важной геометрической формой, которая используется в различных сферах наук и инженерии. Например, она применяется в оптике для описания преломления света, а также в физике и астрономии для моделирования планет и других небесных тел
Размеры и габариты
Шар и сфера имеют также разные свойства геометрических поверхностей. Поверхность шара является гладкой и однородной, в отличие от сферы, у которой поверхность может быть произвольной формы и иметь выпуклые или вогнутые участки.
Размеры шара
Радиус шара является основным параметром, который определяет его размер. Размеры шара могут быть разными, в зависимости от значения радиуса. Чем больше радиус, тем больше размеры шара
Важно отметить, что все плоские сечения шара будут кругами, причем их радиусы будут равны радиусу самого шара
Таблица ниже демонстрирует связь между радиусом и размерами шара:
| Радиус | Размер шара |
|---|---|
| Маленький | Маленький шар |
| Средний | Средний шар |
| Большой | Большой шар |
Таким образом, размеры шара зависят от его радиуса, что является основной характеристикой шара в геометрии.
Размеры сферы
Одним из ключевых параметров сферы является ее размер. Размер сферы определяется диаметром — расстоянием между двумя противоположными точками на ее поверхности, проходящего через ее центр. Диаметр является самой длинной линией, которую можно провести в сфере.
Зачастую размер сферы также описывается радиусом. Радиус сферы — это половина ее диаметра. Радиус является линией, соединяющей центр сферы с любой точкой на ее поверхности.
Размеры сферы могут быть разными. Сферы могут быть очень маленькими, чтобы их нельзя было увидеть невооруженным глазом, или же огромными, например, планетой. Независимо от размера, все сферы имеют одинаковую форму и гладкую поверхность.
Круг в реальной жизни
В реальности можно без особых усилий отыскать множество предметов, по форме тождественных кругу. К примеру, готовый образец круга – а, точнее, множество, — каждый день катается по дорогам поселков и городов. Понятно, что речь идет о колесе. Здесь стоит оговориться: круг не должен быть однотонным, это не обязательно. Он может быть украшен узорами или чем-то еще – от этого форма не изменяется.
Другой пример круга – Солнце
. Да, то самое дневное светило, которое люди лицезреют каждый день. Любознательный читатель заметит, что Солнце – фигура объемная, она не может быть кругом. Это правда. Но маленькая фигура, какой предстает огненная звезда жителям Земли – по сути своей именно круг. Площадь его, конечно, высчитать не получится. Почему? Потому что этот пример приводится только для наглядности, для того, чтобы понять, что такое круг.
Понятие сферы и шара
Если оглядеться вокруг, то можно найти множество шарообразных и сферических объектов в окружающем мире. Такая форма характерна для космических тел, в том числе, нашей планеты. С мячами разнообразных размеров, фактур и цветов люди встречаются во время занятий спортом и на игровых соревнованиях. Многие фрукты и овощи обладают круглой формой. Подобные примеры касаются реальной жизни. В рамках курса стереометрии перечисленные понятия отличаются
Важно уметь разбираться в терминологии и отличать фигуры друг от друга по ряду характерных признаков
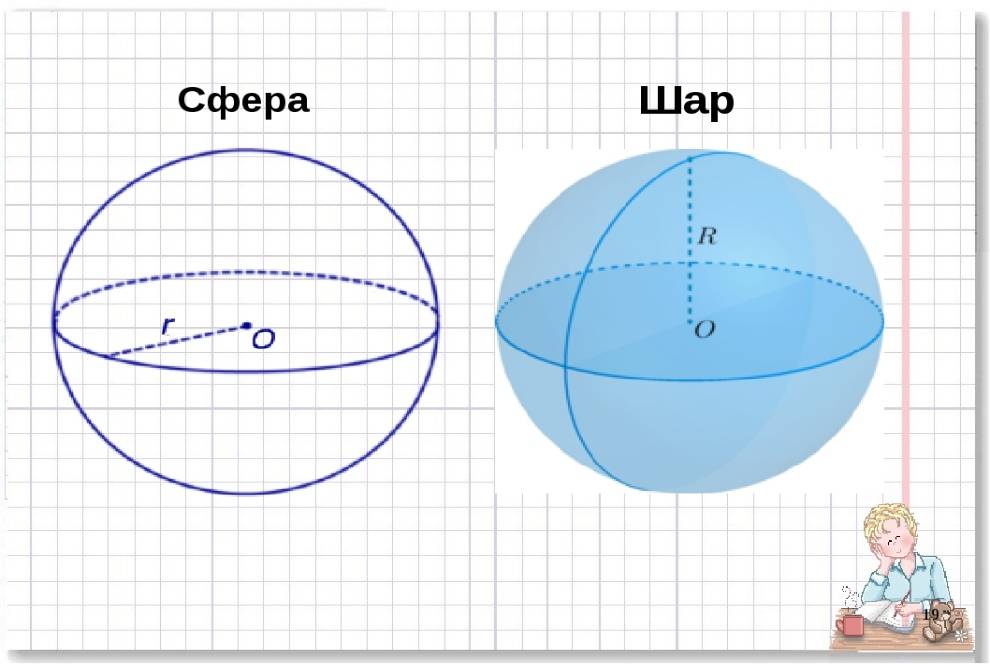
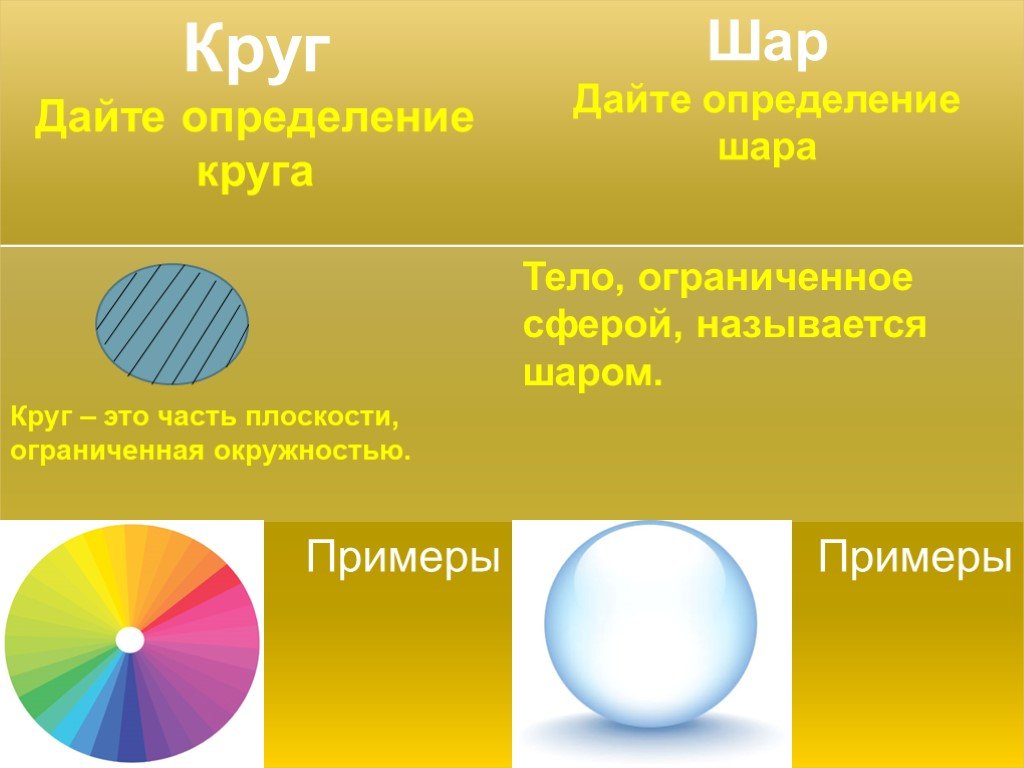
Сферой называют поверхность, в состав которой входит совокупность точек, равноудаленных от какой-то одной центральной точки, называемой центром.
Шар представляет собой материальное тело, в состав которого включены все точки в пространственном измерении, расстояние от которых до определенной центральной точки не более чем заданная величина.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
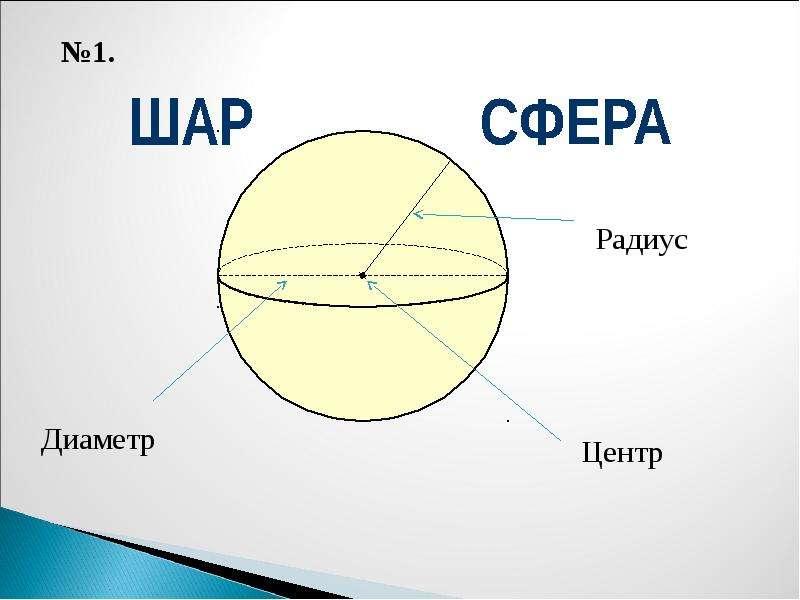
При рассмотрении вышеуказанных понятий часто встречается определение радиуса. Под ним подразумевают прямую, ограниченную парой точек, одна из которых лежит на сфере, а вторая — представляет собой центр этой фигуры. Кроме того, аналогичный отрезок играет роль радиуса шара, помещенного во внутреннее пространство анализируемой сферической фигуры. Наглядно представить эти понятия несложно, если обратиться к изображению, расположенному ниже на рисунке:
Другое важное понятие касается диаметра сферы. Такое название присуще отрезку, пересекающему центральную точку сферической фигуры
При этом начало и конец данной линии расположены на рассматриваемой сфере. Непосредственно сфера является фрагментом шара. Существует аналогичное утверждение, когда окружность признают частью круга. Исходя из расшифровки термина сферы, можно сформулировать справедливое заключение о равенстве радиусов этой фигуры.
Таким образом, центральная точка сферической фигуры делит диаметр пополам. В свою очередь, диаметр сферы в два раза превышает размер радиуса аналогичного объекта. Кроме того, сфера представляет собой тело вращения. Из данного определения можно сделать вывод о способе получения сферической фигуры. Достаточно лишь повернуть половину окружности относительно ее диаметра, чтобы образовалась сфера.
Объем шара
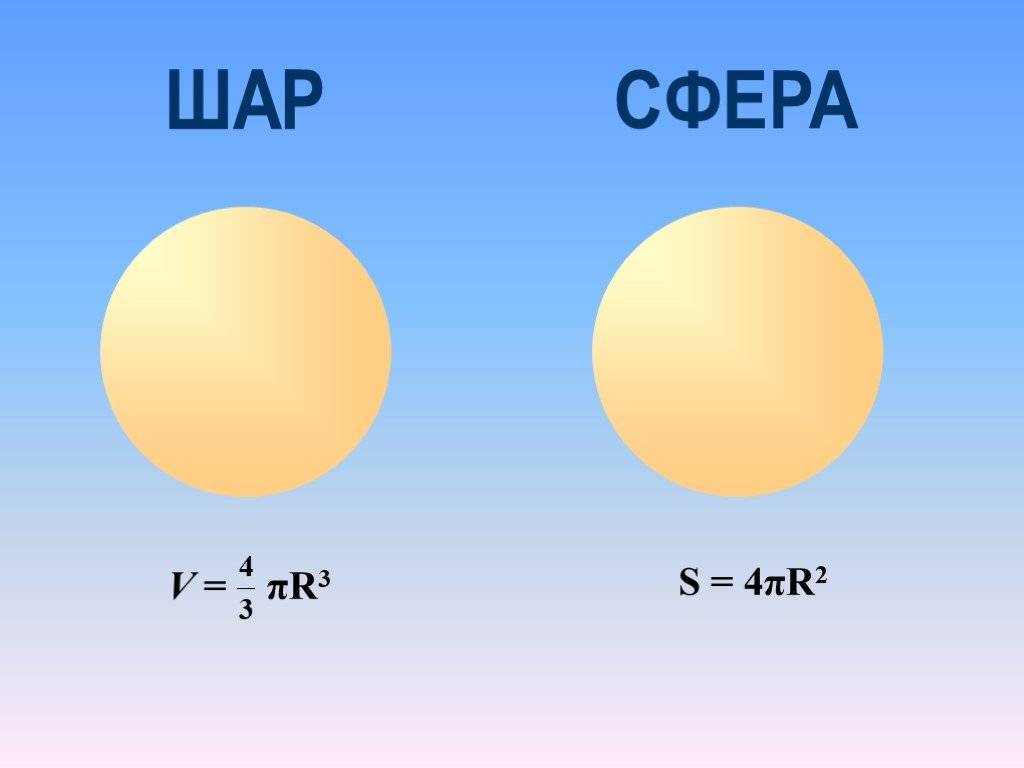
Формула для вычисления объема шара имеет вид:
где R — радиус шара.
Если нужно найти объем шарового сегмента — воспользуйтесь формулой:
V сег =πh 2 (R-h/3), h — высота шарового сегмента.
Площадь поверхности шара или сферы
Чтобы вычислить площадь сферы или площадь поверхности шара (это одно и то же):
где R — радиус сферы.
Архимед очень любил шар и сферу, он даже попросил оставить на его гробницу рисунок, на котором в цилиндр вписан шар. Архимед считал, что объем шара и его поверхность равны двум третьим от объема и поверхности цилиндра, в который вписан шар»
Шар – это тело, состоящее из всех точек пространства, которые находятся на расстоянии, не большем данного от данной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара. Граница шара называется шаровой поверхностью или сферой. Точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, который соединяет центр шара с точкой шаровой поверхности, тоже называется радиусом. Проходящий через центр шара отрезок, который соединяет две точки шаровой поверхности, называется диаметром. Концы любого диаметра называются диаметрально противоположными точками шара.
Шар является телом вращения, так же как конус и цилиндр. Шар получается при вращении полукруга вокруг его диаметра как оси.
Площадь поверхности шара можно найти по формулам:
где r – радиус шара, d – диаметр шара.
Объём шара находится по формуле:
V = 4 / 3 πr 3 ,
где r – радиус шара.
Теорема. Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.
Исходя из данной теоремы, если шар с центром O и радиусом R пересечён плоскостью α, то в сечении получается круг радиуса r с центром K. Радиус сечения шара плоскостью можно найти по формуле
Из формулы видно, что плоскости, равноудалённые от центра, пересекают шар по равным кругам. Радиус сечения тем больше, чем ближе секущая плоскости к центру шара, то есть чем меньше расстояние ОК. Наибольший радиус имеет сечение плоскостью, проходящей через центр шара. Радиус этого круга равен радиусу шара.
Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью, называется большим кругом, а сечение сферы – большим кругом, а сечение сферы – большой окружностью.
Теорема. Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии.
Плоскость, которая и проходит через точку А шаровой поверхности и перпендикулярна радиусу, проведённому в точку А, называется касательной плоскостью. Точка А называется точкой касания.
Теорема. Касательная плоскость имеет с шаром только одну общую точку – точку касания.
Прямая, которая проходит через точку А шаровой поверхности перпендикулярно к радиусу, проведённому в эту точку, называется касательной.
Теорема. Через любую точку шаровой поверхности проходит бесконечно много касательных, причём все они лежат в касательной плоскости шара.
Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Круг ABC – основание шарового сегмента. Отрезок MN перпендикуляра, проведенного из центра N круга ABC до пересечения со сферической поверхностью, – высота шарового сегмента. Точка M – вершина шарового сегмента.
Площадь поверхности шарового сегмента можно вычислить по формуле:
Объём шарового сегмента можно найти по формуле:
V = πh 2 (R – 1/3h),
где R – радиус большого круга, h – высота шарового сегмента.
Шаровой сектор получается из шарового сегмента и конуса, следующим образом. Если шаровой сегмент меньше полушара, то шаровой сегмент дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. Если же сегмент больше полушара, то указанный конус из него удаляется.
Шаровой сектор – это часть шара, ограниченная кривой поверхностью сферического сегмента (на нашем рисунке – это AMCB) и конической поверхностью (на рисунке – это OABC), основанием которой служит основание сегмента (ABC), а вершиной – центр шара O.
Объем шарового сектора находится по формуле:
V = 2/3 πR 2 H.
Шаровый слой – это часть шара, заключённая между двумя параллельными плоскостями (на рисунке плоскостями ABC и DEF), пересекающими сферическую поверхность. Кривая поверхность шарового слоя называется шаровым поясом (зоной). Круги ABC и DEF – основания шарового пояса. Расстояние NK между основаниями шарового пояса – его высота.
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Резюме
И шар, и сфера являются абстрактными геометрическими объектами (геометрическими фигурами), задаваемыми через некоторое геометрическое место точек пространства — например, с помощью понятия центра шара/сферы и радиуса шара/сферы. Однако только шар является полноценным геометрическим телом, поскольку включает в себя не только описание ограничивающей его поверхности, но и всей той части пространства, что в себя эта поверхность заключает. С такой точки зрения сфера — лишь внешняя абстрактная граница (поверхность) задаваемого в пространстве шара.
















Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию
Цель:
познакомить детей с
геометрическими фигурами (шар и куб). Создать
условия для закрепления умения различать и
называть шар (шарик) и куб (кубик).
Задачи:
- научить детей различать и называть
геометрические фигуры (шар и куб); - развивать у детей память и мыслительные
операции (анализ, сравнение); - развивать речь;
- упражнять в счете до пяти;
- упражнять в приемах лепки;
- воспитывать познавательную активность;
Предварительная работа:
С детьми
: Знакомство с кругом и
квадратом. Сравнение геометрических фигур (круг
и квадрат). Упражнение в устном счете до пяти.
Закрепление приёмов лепки. Подготовка для
занятия слайдовой презентации.
С родителями
: Беседа с родителями о
том, чтобы они дома чаще задавали детям вопросы
«Какие предметы похожи на круг?», «Какие
предметы похожи на квадрат?»
Перечень дидактического материала:
Слайды
с заданиями: «Чем отличаются круг и квадрат?»,
«Чем отличаются шар и куб?», «Сколько красных
шаров?», «Сколько зеленых кубиков?», «Сколько
кубиков всего?», слайд с динамической паузой,
слайды с приемами лепки.
Оборудование:
экран для
воспроизведения слайдов, проектор.
Материалы:
клеёнки для лепки
пластилином и пластилин одного цвета на каждого
ребенка.
Слайд 1.
Воспитатель:
Здравствуйте дети. Вы
любите сюрпризы? У меня для вас сюрприз. Смотрите,
кто пришёл к нам в гости.
Слайд 3.
Дети:
Это кубики и шары.
Слайд 4.
Воспитатель:
Давайте внимательно
посмотрим на шары и кубики.
Слайд 5.
Воспитатель:
На какую, уже известную
вам фигуру похож шар?
Дети:
На круг.
Воспитатель:
Правильно на круг.
Слайд 6.
Воспитатель:
На какую, уже известную
вам фигуру похож куб?
Дети:
На квадрат.
Воспитатель:
Правильно на квадрат.
Слайд 7.
Воспитатель:
Посмотрите внимательно и
вспомните, чем отличаются круг и квадрат.
Слайд 8.
Воспитатель:
Что есть у квадрата, и нет
у круга?
Дети:
У квадрата есть углы. У круга нет
углов.
Воспитатель:
Правильно. Круг и квадрат
отличаются углами.
Слайд 9.
Воспитатель:
Подумайте и скажите, чем
отличаются шар и куб.
Слайд 10.
Дети:
Шар от куба отличаются углами.
Воспитатель:
У шара нет углов и
поэтому его можно катать.
Слайд 11.
Воспитатель:
У куба есть углы, это
придает ему устойчивость и поэтому из кубиков
можно строить.
Дети:
Да!
Воспитатель:
Будьте внимательны!
Слайд 13.
Воспитатель:
Сколько красных шаров?
Считаем вместе. Я показываю, вы называете.
Дети:
Один, два.
Воспитатель:
Молодцы!
Слайд 14.
Воспитатель:
Сколько зеленых кубиков?
Считаем вместе.
Дети:
Один, два, три, четыре.
Воспитатель:
Молодцы!
Слайд 15.
Воспитатель:
Сколько кубиков всего?
Считаем вместе.
Дети:
Один, два, три, четыре, пять.
Воспитатель:
Вы хорошо считаете! А
теперь поиграем.
Слайд 16.
Физкультминутка.
Воспитатель:
Слайд 17.
Воспитатель:
Прошу садиться за
рабочие места, чтобы приступить к лепке. Мы будем
лепить кубик и шарик.
(дети садятся за подготовленные столы с
клеёнками и кусочками пластилина
)
Воспитатель:
Сначала нужно разделить
пластилин на две части.
Слайд 18.
Воспитатель:
Возьмите один кусочек
пластилина и придайте ему круглую форму,
раскатывая кругообразными движениями между
ладонями.
Это вы уже умеете и справились хорошо. Проверьте,
катается ли ваш шар.
Слайд 19.
Воспитатель:
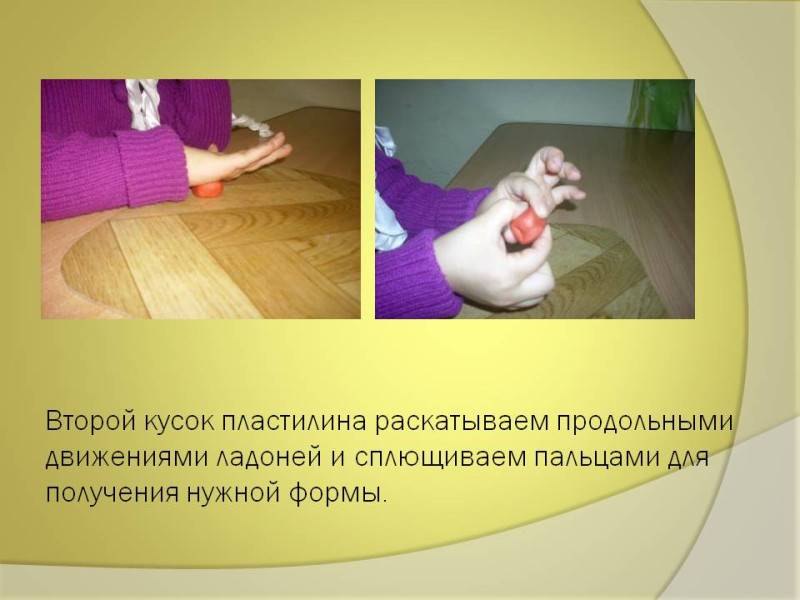
А теперь задача
посложнее – нужно сделать кубик. Будьте
внимательными: кусок пластилина раскатываем
продольными движениями ладоней и сплющиваем
пальцами для получения нужной формы.
Ну что справились? Проверьте, прочно ли стоит ваш
кубик.
Слайд 20.
Воспитатель:
Посмотрите, как Мишка
радуется вашим шарам и кубикам!
– Я тоже очень рада вашей работе!
– Но напомните мне – чем отличается шар от куба?
Дети:
Шар круглый и катается, а кубик с
углами и стоит прочно.
Дети:
Да!
Небольшое погружение в один из разделов математики
Для начала потребуется вспомнить о существовании науки геоме́трии (в несколько вольном переводе с греческого это слово означает «землемеренье») — обособленном разделе математики, специализирующемся на изучении пространственных структур, их отношений между собой и различных возникающих из этого обобщений
Важно, что несмотря на подобное «приземлённое» происхождения названия эта наука оперирует сугубо абстрактными понятиями, которые в привычном нам мире не существуют в прямом физическом воплощении
Одно из таких базовых понятий — это геометрическая точка. Напрягите своё воображение: в отличие от «точки карандашом», «точки от булавки» и так далее эта точка представляет из себя полностью абстрактный объект в воображаемом пространстве без каких-либо измеримых характеристик типа «толщины», «цвета» и так далее (математики любят при этом произносить словосочетание «нульмерный объект»). В принципе, всё остальное в геометрии будет далее определяться исходя именно из этой абстракции.
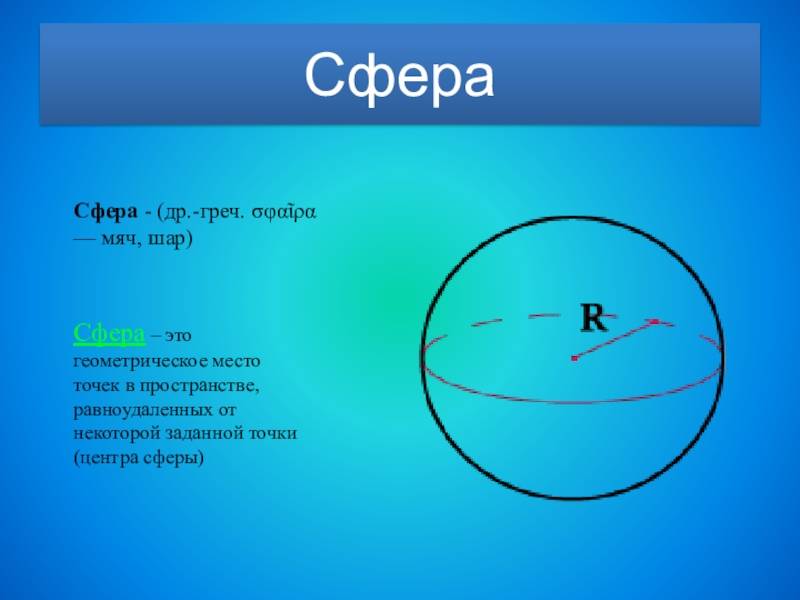
Следующее нужно для дальнейших рассуждений понятие — это «ритуальная» математическая фраза «геометри́ческое ме́сто то́чек» (ГМТ). C её помощью описывается некоторое множество (совокупность) точек, подпадающих под определённое отношение (свойство) — таким образом задаётся «геометрическая фигура». Пример: сфе́ра (от древнегреческого σφαῖρα, изначально обозначающего мяч/шар) — это геометрическое место таких точек пространства, которое можно описать как равноудалённое (находящееся на строго одном расстоянии) от некоторой заданной точки, обычно называемой «центром сферы».
Сфера
Расстояние же от центра сферы до этого ГМТ принято называть «радиусом сферы»
Во время всех этих манипуляций важно продолжать помнить, что сфера — понятие более эфемерное, чем даже всем привычный и знакомый мыльный пузырь: у любого мыльного пузыря всё-таки есть вполне ощутимая стенка из водно-мыльной плёнки микроскопической толщины, которую можно физически измерить (и даже проткнуть), а у сферы — нет!
Сфера и радиус сферы
Теперь обратимся к определению шара: под шаром понимается совокупность всех таких точек пространства, что находится от определённой точки (центра шара) на расстоянии, не большем заданного (радиуса шара). Иначе говоря, шар является «геометрическим телом» — тем, что согласно первичному определению Евклида «имеет длину, ширину и глубину» (в современных учебниках это определение менее наглядно: «часть пространства, ограниченная своей образуемой формой»).
Шар
Попутно отметим, что использованные здесь способы задания сферы и шара через центр и радиус — не единственные: например, задание сферы/шара в пространстве можно выполнить посредством вращения окружности, круга и т.д. (глубоко заинтересовавшимся этим вопросом настоятельно рекомендуется ознакомиться с отдельным разделом геометрии под названием «Фигуры и тела вращения», поскольку это часто применяемый способ задания самых различных геометрических фигур и тел в пространстве).
Таким образом, и в случае сферы, и в случае шара приходится иметь дело с определённым образом заданным геометрическим местом точек (то есть геометрической фигурой), однако лишь в случае шара можно говорить о геометрическом теле. Любопытно отметить, что строго говоря сферу из шара можно «вычесть»: в этом случае математики говорят об «открытом шаре». Однако «по умолчанию» имеет место «замкнутый шар», где сфера является его естественной границей и принадлежащей ему частью.
Разница между шаром и сферой
Когда людям задают вопрос, чем отличается сфер от шара, многие попросту пожимают плечами, думая, что фактически это одно и то же (аналогия с кругом и окружностью).
В повседневной жизни мы редко говорим сфера, чаще шар или шарик. И не все понимают какая разница между этими двумя геометрическими понятиями. Наверное можно сказать, что сфера это внешняя оболочка шара. Воздушный шарик, например, на самом деле не шар, а сфера. При условии, конечно, его абсолютной «круглости». Как я понимаю, то у шара абсолютно все точки поверхности равноудалены от его центра, а у сферф это условие не является обязательным.
Апельсин, футбольный мяч, арбуз, похожи на шар. Из всех тел заданного объёма шар имеет наименьшую поверхность. Поверхность шара называют сферой. Расстояние от точек сферы до её центра называется радиусом сферы и обычно обозначается R. Радиусом также называется любой отрезок, соединяющий точку сферы с её центром.
Определение.Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Любой диаметр соответствует 2-м радиусам. Часть шара (сферы), которая отсекается от него любой плоскостью (ABC), является шаровым (сферическим) сегментом. Круги ABC и DEF – основания шарового пояса. Расстояние NK между основаниями шарового пояса – его высота. 1/3 произведения площади поверхности шара на длину радиуса. Зачастую озвучивают так: объём шара равен 1/3 произведения поверхности шара на его радиус.
Все эти точки находятся от центра геометрического тела на расстоянии, которое не больше заданного. Само данное расстояние называется радиусом. От центра сферы все точки в пространстве равноудалены.
Образованная фигура – будет шар. Поэтому шар называют также телом вращения. Возьмем какую-нибудь плоскость и разрежем ею наш шар. Подобно тому как мы режем ножом апельсин. Кусок, который мы отсечем от шара, называется шаровым сегментом.
Когда людям задают вопрос, чем отличается сфер от шара, многие попросту пожимают плечами, думая, что фактически это одно и то же (аналогия с кругом и окружностью). Действительно, все ли из нас хорошо знают из школьной программы геометрию и могут сходу ответить на данный вопрос? Сфера имеет некоторые отличия от шара, которые нужно знать не только школьникам, чтобы получить хорошую оценку за свои продемонстрированные знания, но и многим другим людям, например, чья работа непосредственно связана с чертежами.