Чем отличается ромб от квадрата

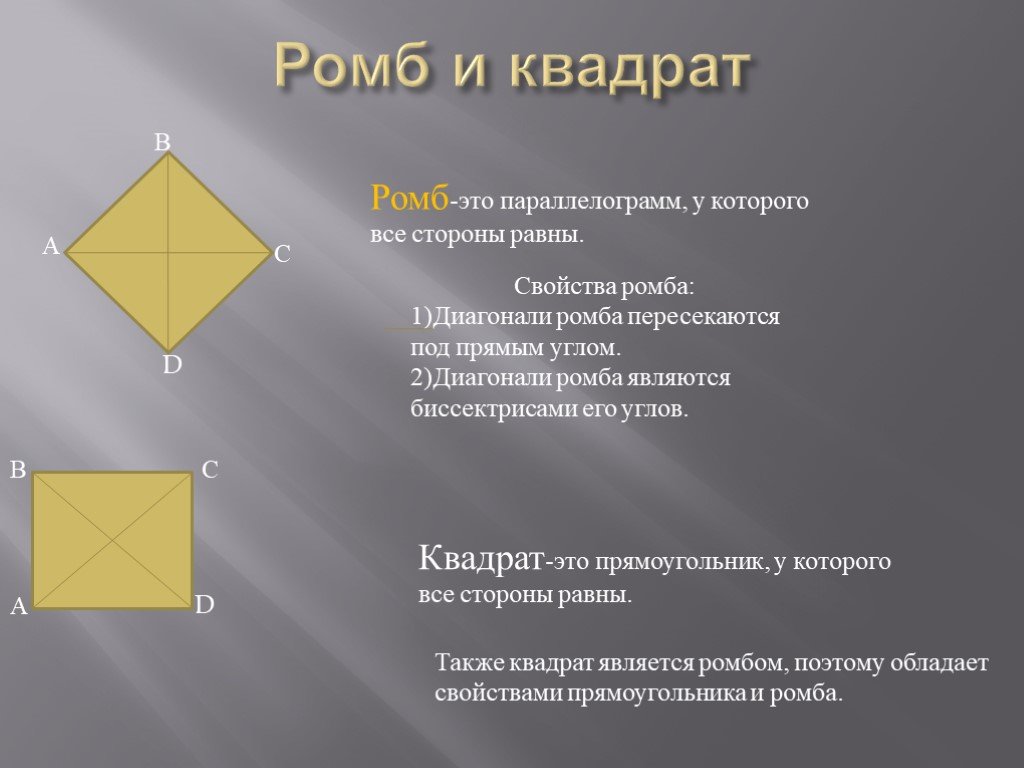
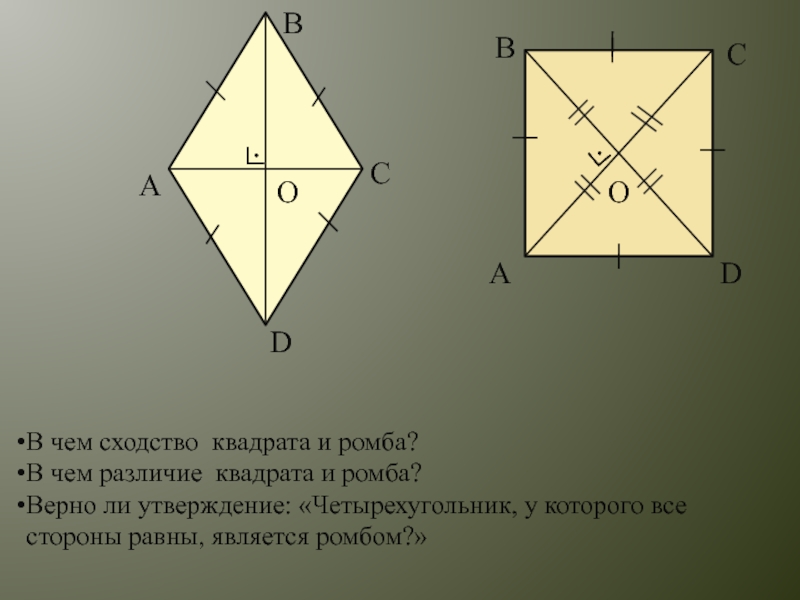
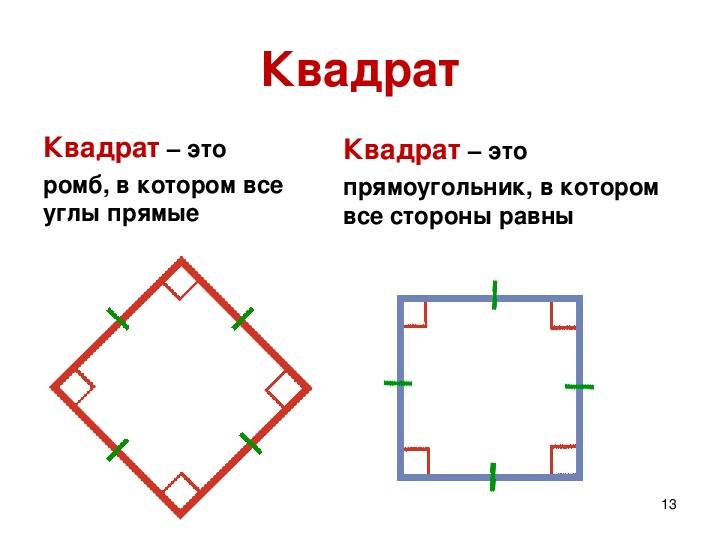
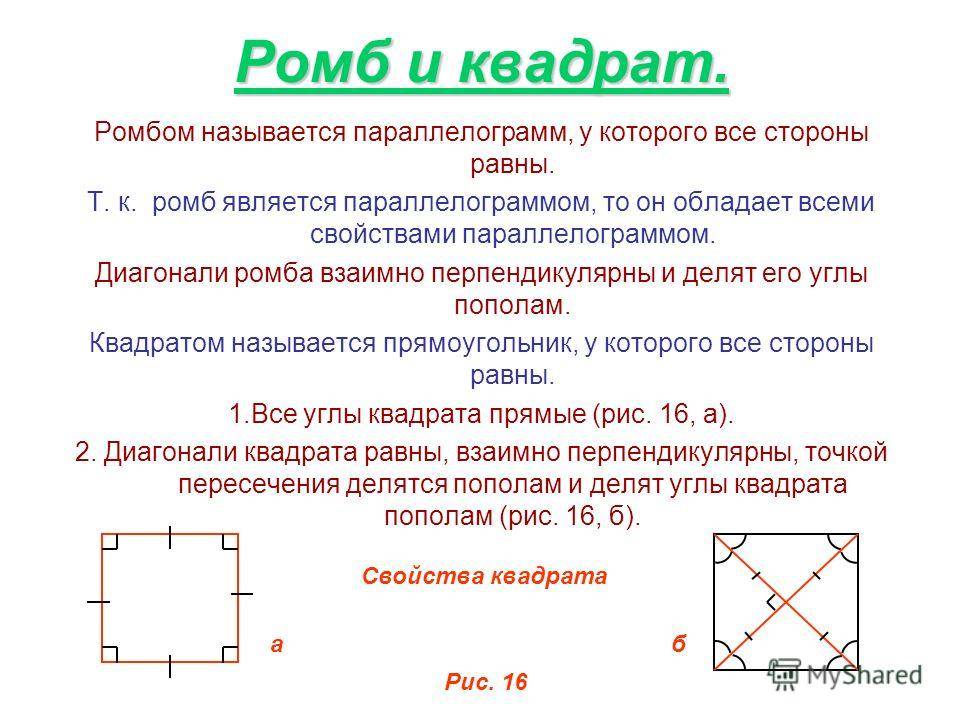
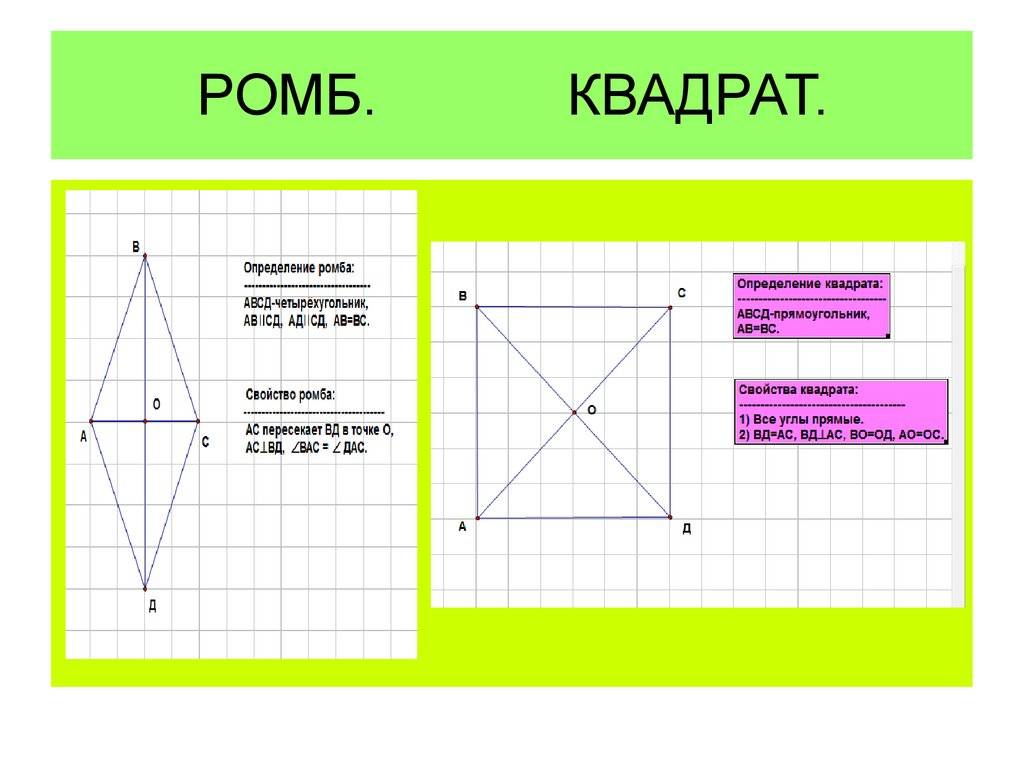
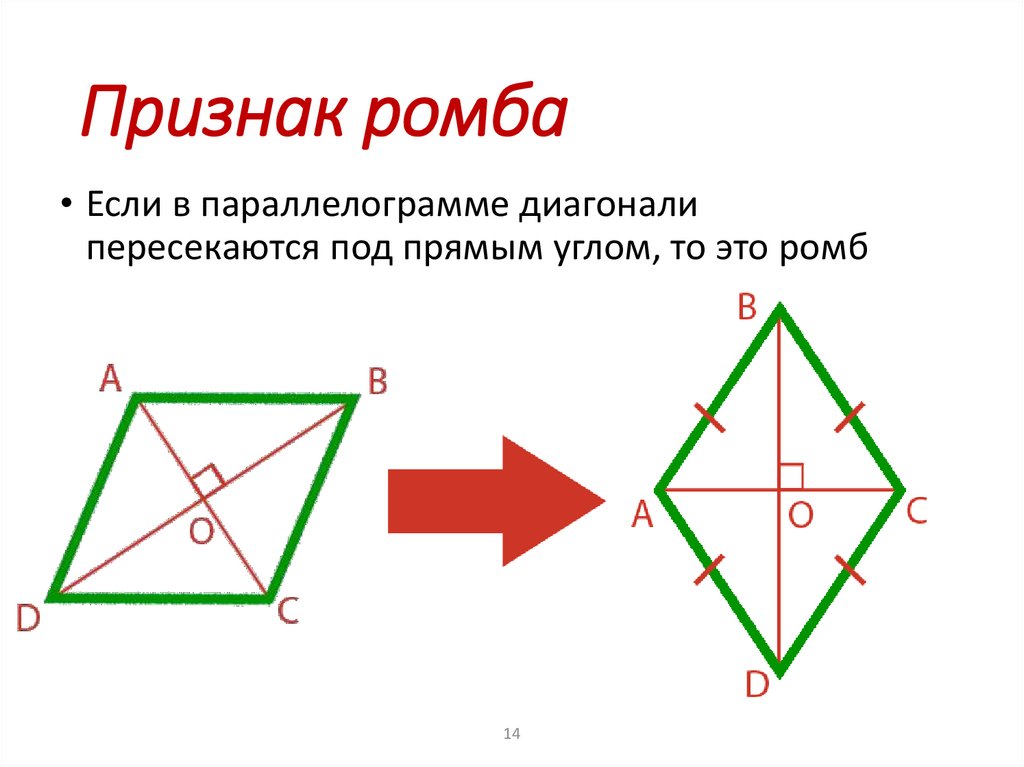
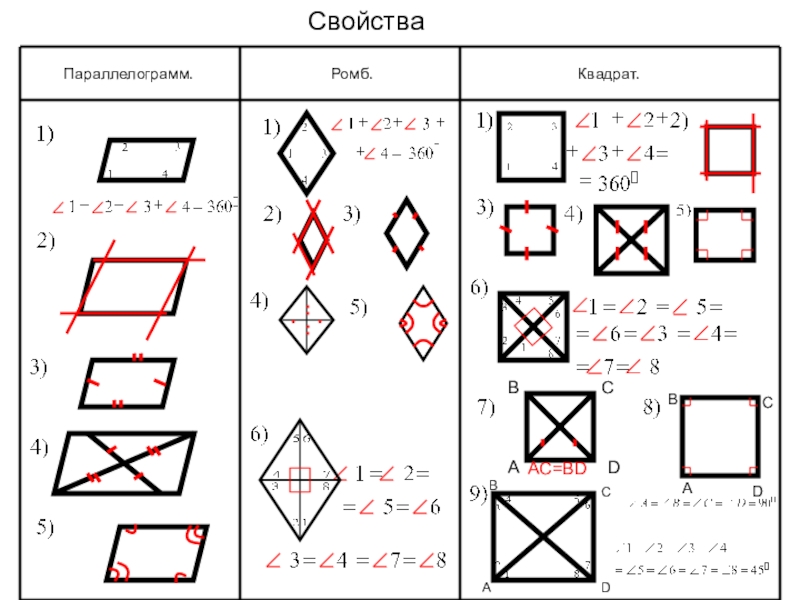
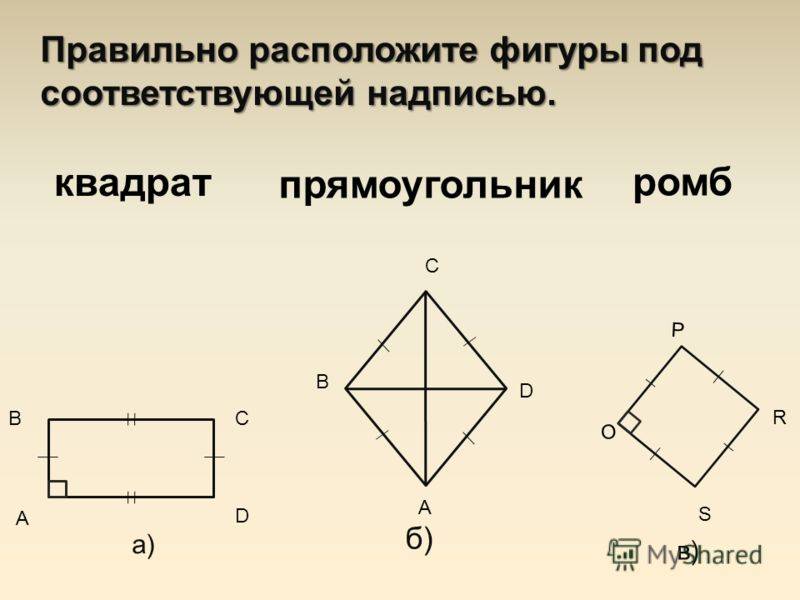
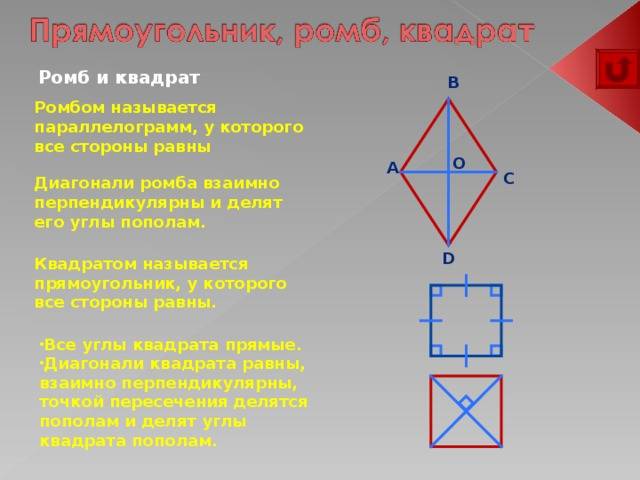
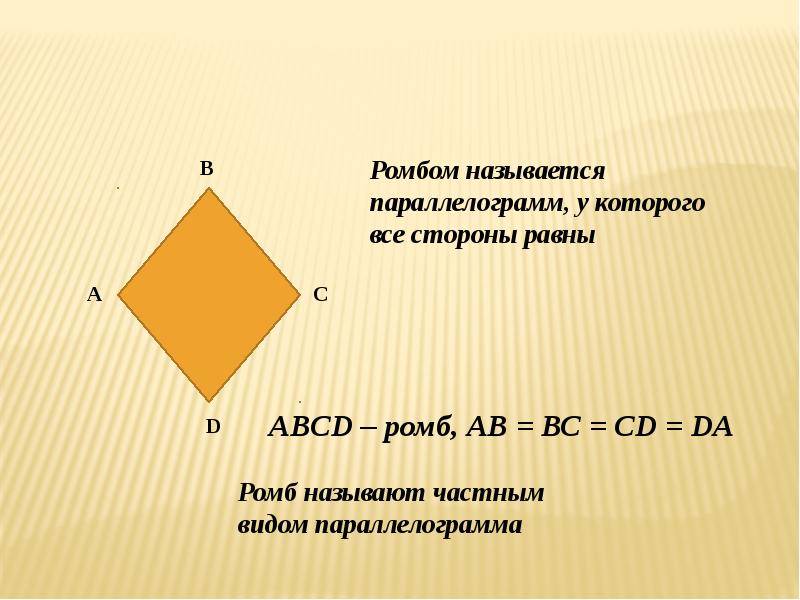
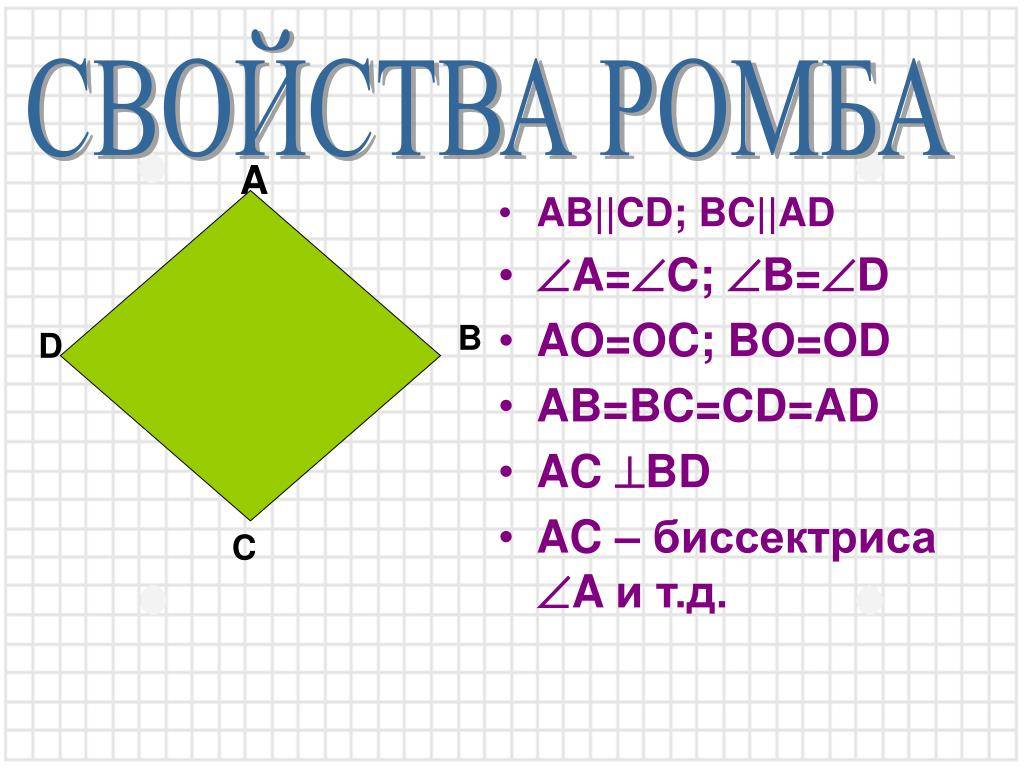
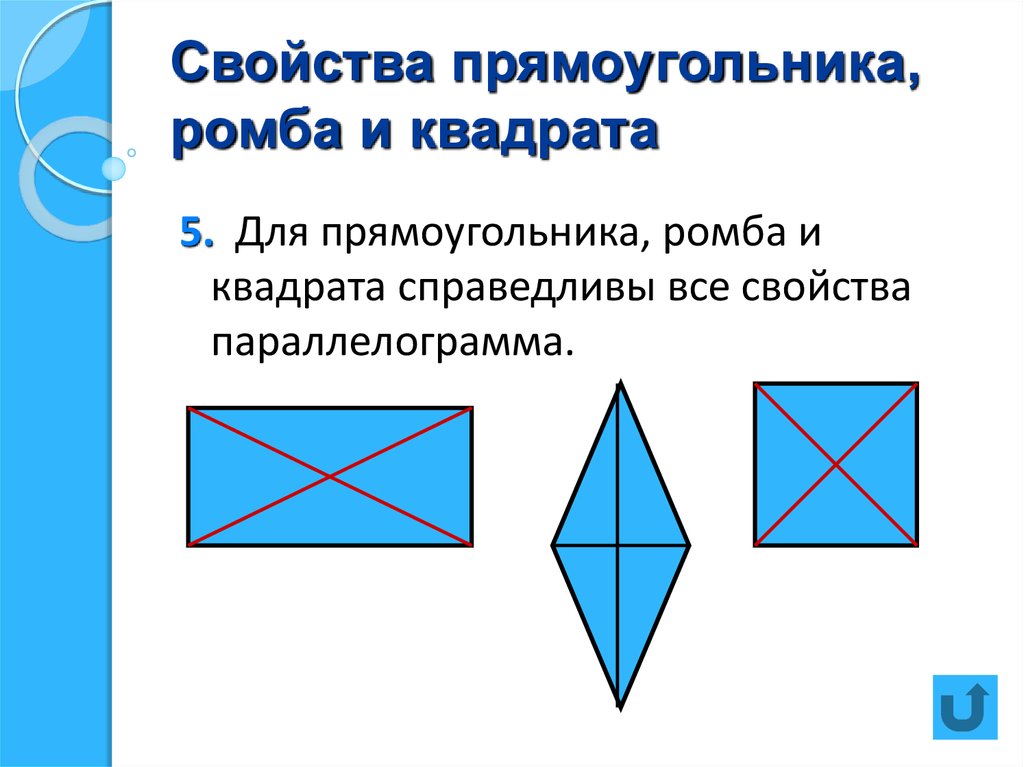
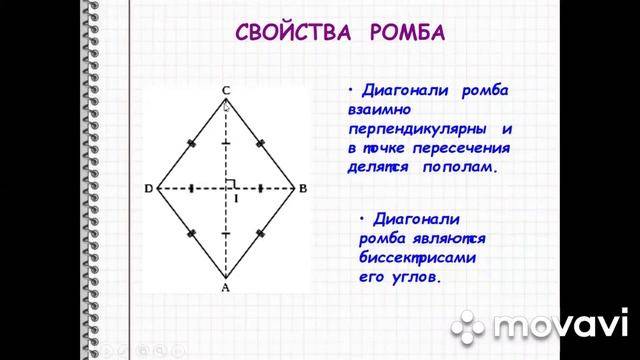
Определение ромба, как геометрической фигуры

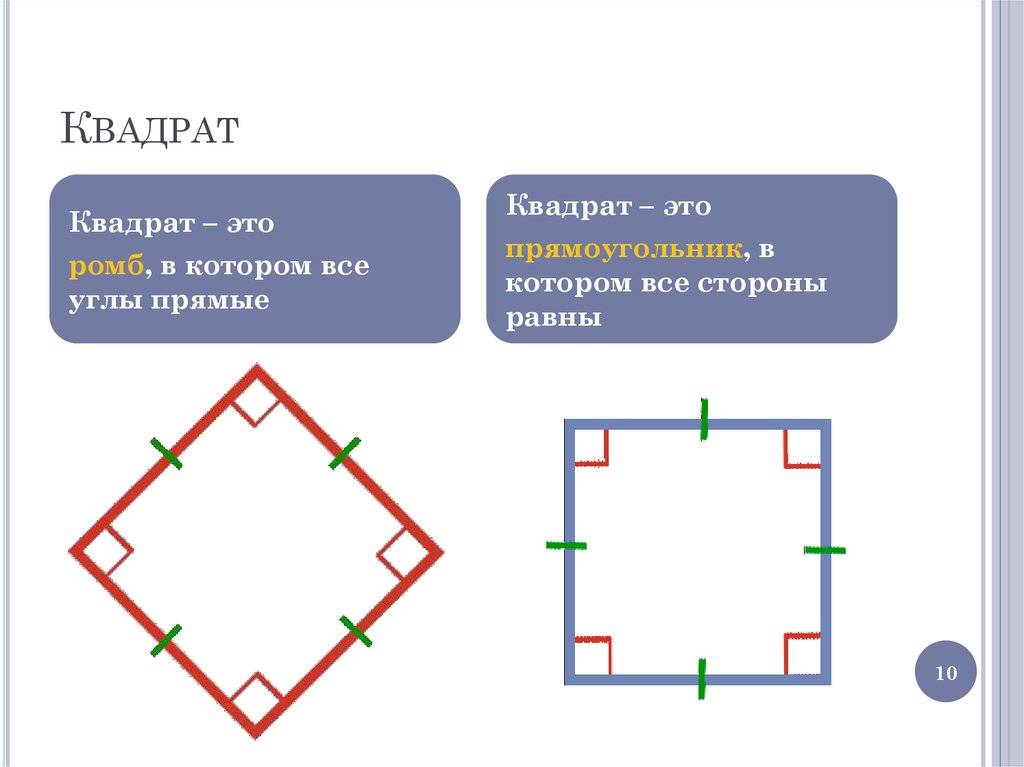
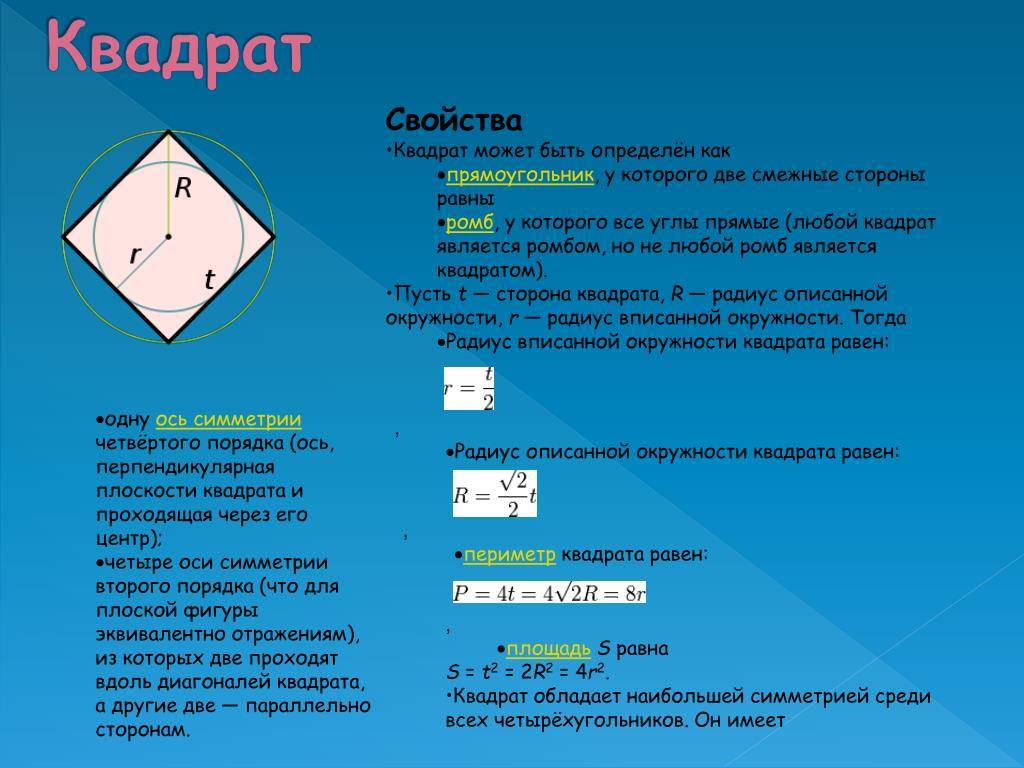
Ромб – это такой параллелограмм, у которого все стороны равны. Если же ромб имеет прямые углы, то он называется квадратом.

Сам термин “Ромб” в переводе с греческого языка, обозначает “бубен”. Конечно же в нашем понимании бубен, как музыкальный инструмент, имеет круглую форму. Но это сейчас бубны делают круглыми, а в древние времена он как раз и имел квадратную форму или форму ромба.

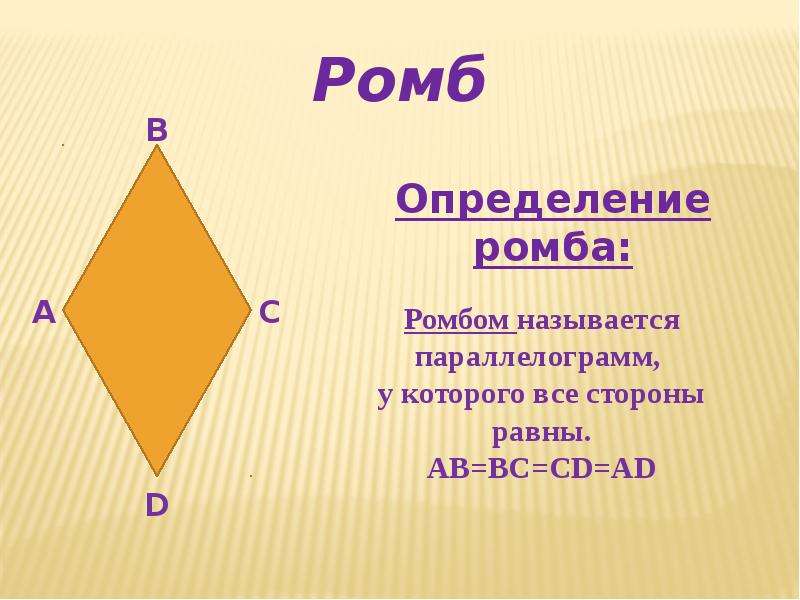
Давайте остановимся на основных определениях ромба и попробуем понять, что же являет собой эта геометрическая фигура.

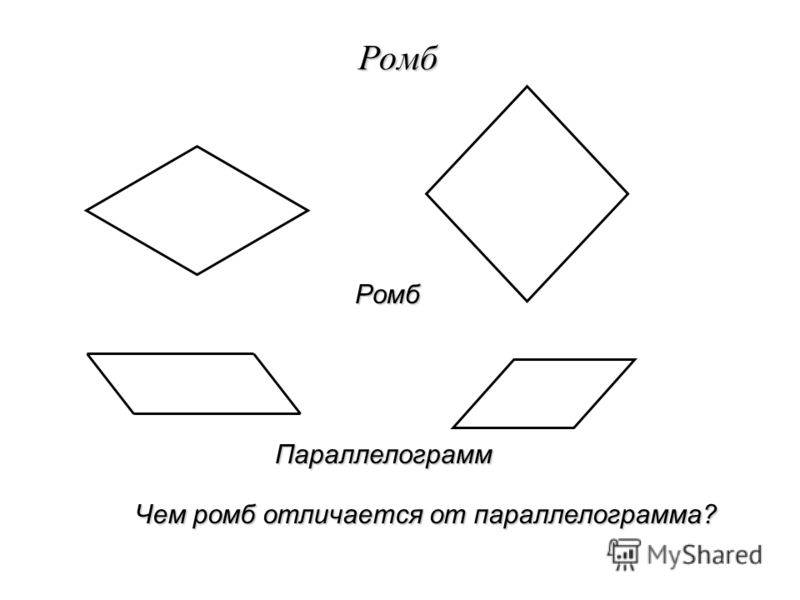
Ромб – это такой равносторонний параллелограмм, у которого равные стороны, но неравные углы.

В отличие от квадрата, ромб – это равносторонний косоугольник.

Как всегда мы получаем множество определений той или иной геометрической фигуры, но это не означает, что каждый ученик должен сесть и «зазубрить» именно эти определения. Отличие в определениях – это насколько широко они описывают нашу геометрическую фигуру. Самое главное, это понимание о чем говориться в определении и возможность представить фигуру. Если вы будете придерживаться этих двух правил, то и сами сможете написать или дополнить парочку определений.

Задачи на ромб и квадрат

Теперь рассмотрим несколько задач, в которых встречаются ромб и квадрат.

Задача 1.

В ромбе одна из диагоналей равна стороне (см. Рис. 2). Найти:

а) углы ромба;

б) углы между диагоналями и сторонами.

Дано: – ромб; .

Найти: а) ; б) .

Решение:

Рис. 2

а) (так как у ромба все стороны равны). Значит, треугольник – равносторонний. Отсюда следует, что угол . Так как в любом параллелограмме сумма соседних углов равна , то .

Ответ: .

б) По доказанной выше теореме: . Аналогично получаем, что .

Ответ: .

Задача 2.

Найти периметр ромба , в котором , а меньшая диагональ равна . Найти периметр ромба.

Дано: – ромб; .

Найти:

Решение:

Рис. 3

Рассмотрим треугольник , в нём: . Значит, данный треугольник равнобедренный, угол при вершине у него равен , два других угла при основании равны, поэтому данный треугольник – равносторонний. Значит: . Так как в ромбе все стороны равны, то периметр ромба равен: .

Ответ: .

Задача 3.

Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен .

Найти:

Решение:

Рис. 4

Вспомним, что в любом параллелограмме противоположные углы, а сумма углов, прилежащих к одной стороне, равна . Из этого следует, что: . Теперь воспользуемся доказанной вначале теоремой: .

Ответ:

Задача 4.

Докажите, что параллелограмм является ромбом, если:

а) его диагонали взаимно перпендикулярны;

б) его диагонали являются биссектрисами углов.

а) Дано: – параллелограмм, .

Доказать: – ромб.

Доказательство:

Рис. 5

Рассмотрим треугольник : в нем является одновременно и высотой (так как диагонали перпендикулярны), и медианой (так как диагонали в любом параллелограмме точкой пересечения делятся пополам). Значит, – равнобедренный. Из этого следует, что: . Если теперь воспользоваться тем, что в параллелограмме противоположные стороны равны, получаем, что: . То есть – ромб.

Доказано.

б) Дано: – параллелограмм, – биссектрисы углов параллелограмма.

Доказать: – ромб.

Доказательство:

Рис. 6

Рассмотрим треугольник : в нем является одновременно и биссектрисой (так как диагонали являются биссектрисами углов), и медианой (так как диагонали в любом параллелограмме точкой пересечения делятся пополам). Значит, – равнобедренный. Из этого следует, что: . Если теперь воспользоваться тем, что в параллелограмме противоположные стороны равны, получаем, что: . То есть, – ромб.

Доказано.

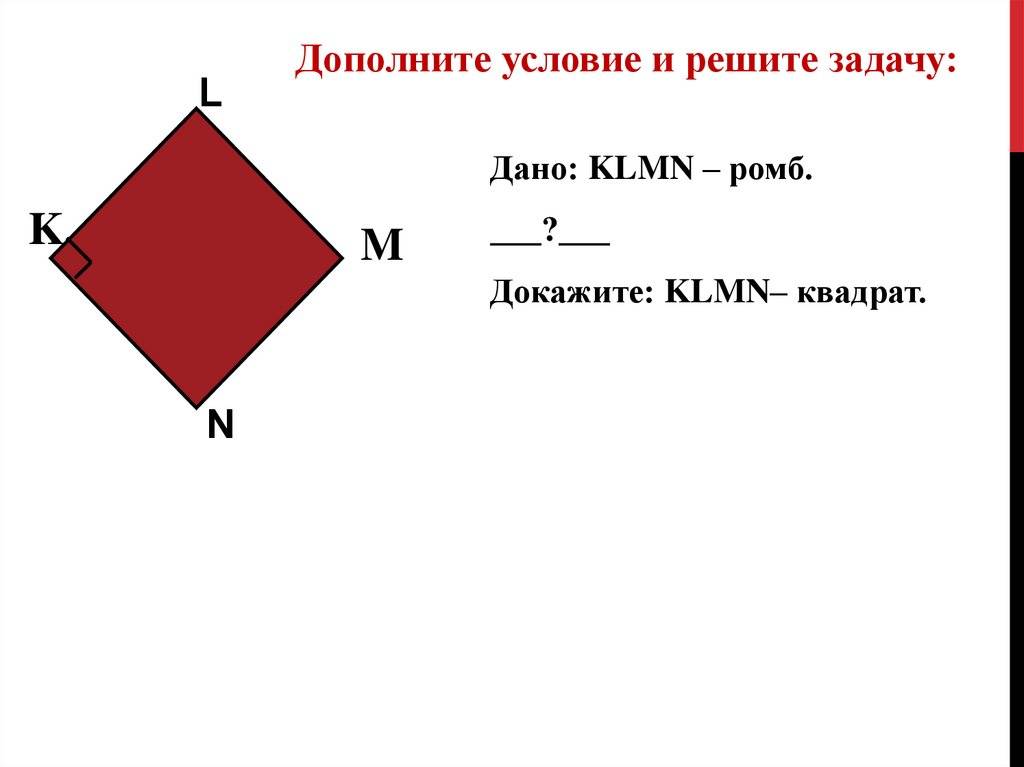
Задача 5.

Доказать: – квадрат.

Доказательство:

Рис. 7

Вспомним, что квадрат – это одновременно прямоугольник и ромб. Если говорить о сформулированном строгом определении, то квадрат – это прямоугольник, у которого все стороны равны. Равенство сторон следует из того, что данный четырёхугольник – ромб. Осталось доказать, что он является ещё и прямоугольником. По условию: (у любого параллелограмма противоположные углы равны). Кроме того, сумма соседних углов параллелограмма равна . Значит: . Отсюда мы получаем, что – прямоугольник, а значит, и квадрат.

Доказано.

На этом уроке мы изучили ромб и квадрат, а также рассмотрели их свойства и решили различные задачи, в которых встречаются ромб и квадрат.

ИСТОЧНИК

http://x-uni.com/geometriya/8-klass/video/romb-i-kvadrat

https://www.youtube.com/watch?v=axMe7L_01j0

https://www.youtube.com/watch?v=y4x7r57AuSM

https://www.youtube.com/watch?v=9qbxjBa2uSs