Разница между овалом и эллипсом

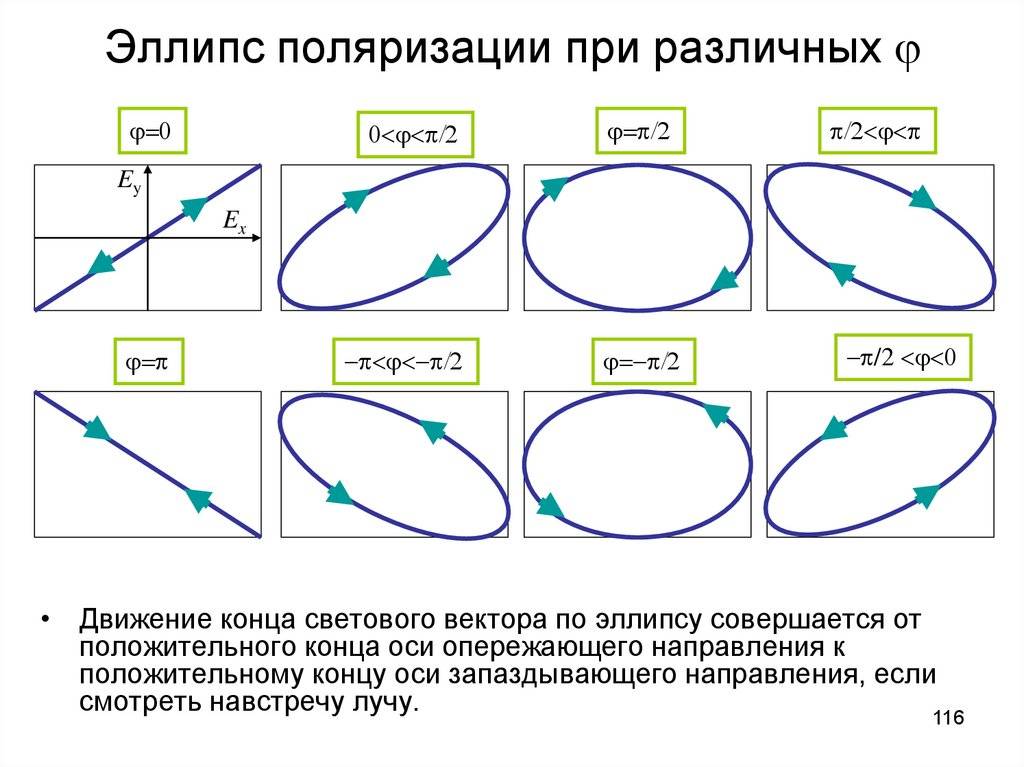
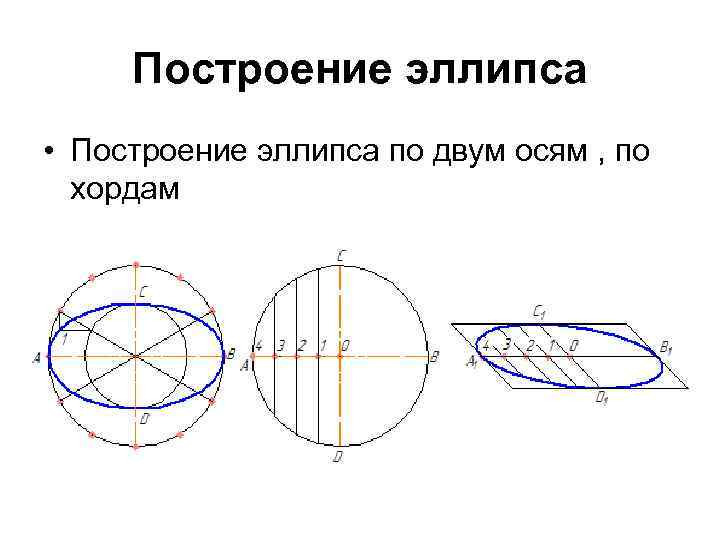
Сходства и различия между фигурами

Тут очень важна симметричность

Симметрия – это фундаментальное понятие в математике и науке, которое относится к свойству иметь последовательную схему или структуру, которая остается неизменной при определенных преобразованиях. Это понятие можно наблюдать в различных областях, таких как искусство, дизайн и геометрия, где оно играет важную роль в создании эстетически приятных и хорошо сбалансированных композиций.

В искусстве и дизайне симметрия используется для создания гармонии и баланса между различными элементами произведения. Используя симметричные конструкции, художники и дизайнеры могут создавать узоры и композиции, которые кажутся организованными и визуально привлекательными. Это может варьироваться от простой двусторонней симметрии в логотипах и типографике до более сложной радиальной симметрии в мандалах и других декоративных мотивах.

В геометрии симметрия играет важную роль в понимании свойств фигур и их отношений друг с другом. Симметрию можно использовать для классификации различных типов геометрических фигур и определения их уникальных характеристик. Например, правильные многоугольники обладают вращательной симметрией, потому что их можно поворачивать на определенные углы, и они все равно будут выглядеть одинаково.

Симметрия – это важная концепция, которая помогает понять и оценить красоту и порядок в окружающем нас мире.

Овал и эллипс – это две фигуры, которые имеют общие черты, но также и явные различия. Обе фигуры вытянутые и асимметричные, без прямых линий и углов. Кроме того, обе они имеют изогнутый периметр, который можно использовать для создания эстетически привлекательных конструкций и узоров.

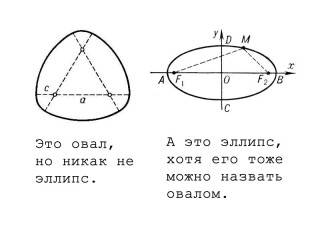
Однако между овалом и эллипсом есть различия. Овал – это тип фигуры, похожий на уплощенный круг. Он имеет два разных радиуса, причем один радиус больше другого. Это приводит к неравномерной кривизне и придает овалу характерную асимметрию. Термин «овал» часто используется как взаимозаменяемый с термином «эллипс», но, строго говоря, эти две формы не являются одним и тем же.

С другой стороны, эллипс – это абсолютно симметричная фигура, определяемая двумя осями, которые пересекаются в его центре. Эта фигура образуется путем проведения плоскости и рассечения ее через конус под определенным углом. В результате получается гладкая кривая с постоянной шириной, без углов и краев. В отличие от овала, он имеет два равных радиуса, в результате чего получается идеально симметричная форма. В итоге, хотя обе формы похожи своей вытянутостью и кривизной, овал асимметричен с двумя разными радиусами, в то время как эллипс идеально симметричен с двумя равными радиусами.

Что такое овал и эллипс

Овал
– это замкнутая вытянутая геометрическая фигура, обладающая правильной формой и особыми свойствами. Вписанная в окружность, она обладает как минимум 4 точками экстремума, то есть вершинами. Если разделить овал прямой линией по двум противоположным вершинам, то два сегмента, полученные в результате данного действия, будут абсолютно идентичными.Эллипс
– это замкнутая плоская кривая, частный случай овала, у которого имеется 4 вершины в точках экстремума. Центральная ось, проведённая по двум противоположным точкам экстремума, содержит две точки фокуса, равноудалённые от вершин. Сумма расстояний от фокусов до любой точки на кривой эллипса – постоянная величина, которая равна длине центральной оси.Эллипс

Эллипс: определение и свойства

Эллипс имеет две оси — большую и малую. Большая ось, также называемая длинной полуосью, проходит через два фокуса и центр эллипса. Малая ось, называемая короткой полуосью, проходит через центр и перпендикулярна большой оси.

Форма эллипса кажется симметричной относительно его центра, и его площадь может быть вычислена по формуле S = π а b, где а и b — длины полуосей.

Периметр эллипса также может быть вычислен с помощью формулы P ≈ 2π √(a² + b²/2), где а и b — длины полуосей.

Один из основных отличий эллипса от овала состоит в том, что все точки эллипса находятся на одинаковом расстоянии от двух фокусов, в то время как в овале эти расстояния могут отличаться.

Эллипс имеет ряд уникальных свойств и присутствует во многих аспектах природы, включая движение планет вокруг Солнца и форму некоторых облаков и камней.

Определение эллипса

У эллипса есть две оси — большая ось (a) и малая ось (b). Большая ось является длиннейшей прямой, проходящей через центр эллипса и соединяющей два противоположных вершины. Малая ось же проходит через центр эллипса, перпендикулярно к большей оси и соединяет два противоположных конца эллипса.

Длина большой оси равна двойному радиусу, так как радиус является половиной большой оси. Формула для определения длины большой оси эллипса — a = 2r.

Длина малой оси также равна двойному радиусу, поскольку радиус является половиной малой оси. Формула для определения длины малой оси эллипса — b = 2r.

Площадь эллипса можно вычислить с помощью формулы: S = π * a * b, где π — это число пи (приближенное значение 3,14159).

Периметр эллипса также может быть вычислен с помощью формулы: P = 2π * sqrt((a^2 + b^2)/2), где sqrt — квадратный корень, и ^ — значит возведение в степень.

Одно из отличий эллипса от овала заключается в том, что эллипс имеет симметричную форму, в то время как овал — неравномерный и несимметричный.

Эллипс является геометрической фигурой, которая встречается в природе, например, в форме орбит планет вокруг Солнца или в форме кометы при ее движении вокруг Солнца.

Математические свойства эллипса

Одной из важных характеристик эллипса является его форма. Форма эллипса может быть размерной или безразмерной. Размерная форма характеризуется показателем эксцентриситета, определяющего степень сжатия или растяжения эллипса. Безразмерная форма характеризуется отношением длины большой оси к длине малой оси, называемым аспектом.

Площадь эллипса вычисляется по формуле S = π * a * b, где a и b — полуоси эллипса. Периметр эллипса вычисляется по формуле P = 4 * а * E(1 — e^2), где Е — числовой эксцентриситет эллипса.

Эллипс имеет две оси — большую (а) и малую (b). Оси эллипса являются симметричными относительно центра. Длина большой оси обозначается как 2a, а длина малой оси — как 2b. Расстояние от центра эллипса до фокуса (f1 и f2) называется фокусным радиусом.

Эллипс имеет следующие математические свойства:

• Сумма расстояний от любой точки эллипса до фокусов равна длине большой оси.
• Произведение расстояний от любой точки эллипса до фокусов равно площади эллипса.
• Расстояние от центра эллипса до любой точки на эллипсе равно радиус-вектору этой точки.
• Эллипс — кривая второго порядка, которую можно задать уравнением вида (x^2/a^2) + (y^2/b^2) = 1, где x и y — координаты точки на эллипсе.

Эти свойства позволяют различать эллипс от других фигур и использовать его в различных областях математики и природных наук.

Идентификация эллипсовидных овальных кривых

Итак, для идентификации предлагаются следующие кривые: эллипс, овал Кассини, гиперэллипс Ламе; гипоэллипс Ламе; гипергипоэллипс Ламе; овал R­0; овал R­1; циклоидальный овал; гиперовал Rr; гипоовал Rr; гипергипоовал Rr. Зная геометрию и свойства данных кривых, классификацию можно выполнить визуально, однако иногда  некоторые из них бывают очень схожи.

Идентификацию лучше проводить в той CAD­программе, в которой эти кривые созданы. Автор для построения и идентификации кривых использовал  программу КОМПАС.

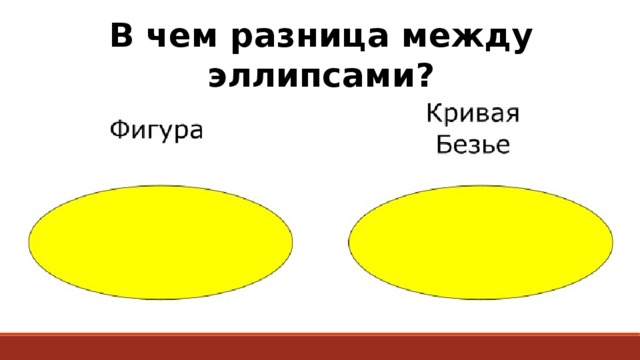
При поочередном входе в режим редактирования кривых можно сразу распознать эллипс и все овалы по сопрягаемым дугам окружностей, группу которых определяем сопряжением с эллипсом. Все остальные кривые при редактировании покажут, что построены с помощью кривой Безье.

Оставшиеся кривые сначала необходимо разбить на группы в соответствии с нашей классификацией путем сопряжения с соответствующими им эллипсами.

В группе гипергипоовалов окажется только гипергипоэллипс, так как гипергипоовал Rr распознан уже на первой стадии идентификации.

Далее рассмотрим группу гипоовалов. Поскольку гипоовал Rr также распознан на первой стадии, в ней остаются: кривая R­0; кривая R­1; гипоэллипс Ламе; циклоидальный овал. Последний распознаем с помощью эксцентриситет­константы циклоидального овала (пригодилась!). Для этого поочередно для каждой кривой рассчитываем фокальный радиус, умножая размер большой полуоси на эксцентриситет­константу Eco. Тот овал, в котором пучок из восьми лучей, выпущенных из фокуса и отраженных от кривой, соберется в противоположном фокусе, и будет циклоидальным овалом. Для распознавания оставшихся трех гипоовалов рассмотрим три возможных сценария идентификации. Все зависит от количества фокусов у гипоэллипса Ламе. Первый вариант — кривая Ламе имеет четыре фокуса (например, при сочетании параметров: a/b = 7/10; n = m = 1,7). В этом случае удается распознать все кривые: бесфокусную R­0, двухфокусную R­1 и четырехфокусную  кривую Ламе.  Второй вариант — кривая Ламе бесфокусная (например, при сочетании параметров: a/b = 8/10; n = m = 1,7). При этом сможем распознать только R­1. Кривая R­0 и гипоэллипс будут трудноразличимыми. Третий вариант — кривая Ламе имеет два фокуса (например, при сочетании параметров: a/b = 8/10; n = 1,7 и m=1,9). Выявить при этом удастся  только кривую R­0. Различить R­1 и гипоэллипс Ламе можно по форме кривых и расположению фокусов… 

Осталось разобраться с гиперовалами. После первой стадии идентификации, где был определен гиперовал Rr, их у нас осталось два: овал Кассини и гиперэллипс Ламе. Для идентификации их в первую очередь необходимо выровнять масштабированием размеров овалов по высоте. Далее нужно определить положение фокусов (тех, которые фигурируют в определении овала Кассини) относительно центра и нанести их. Оптические фокусы овалов использовать нельзя — у них другие координаты. Та кривая, на которой будет соблюдено следующее условие: произведение расстояний от любой точки кривой до фокусов есть величина постоянная, — и есть овал Кассини. Если степени гиперэллипса Ламе равны 2,5 и более, то кривые хорошо различимы визуально — кривая Ламе более угловатая.

Выводов делать не будем. Главное, что почти все точки над «о» расставлены. 

Использование в искусстве

В живописи и графике эллипсы и овалы часто используются для создания изображений различных объектов и предметов: от лица и тела человека до растений и архитектурных деталей. Их гармоничная форма позволяет художникам создавать эстетически привлекательные и сбалансированные композиции.

В скульптуре эллипсы и овалы могут быть использованы для создания объемных форм и плавных линий. Они могут быть основой для моделирования лица, тела или абстрактных скульптурных композиций. Благодаря своей органической форме, эллипсы и овалы помогают придать скульптуре гармонию и естественность.

Архитектура также может вдохновляться эллипсами и овалами. Эти формы могут быть использованы для создания арочных проходов, оконных оформлений, а также для проектирования зданий и сооружений. Овальные формы, например, могут придавать зданию элегантность и изящество.

Также эллипсы и овалы могут использоваться в оформлении интерьеров, деталей мебели и предметов декора. Их гладкие и изящные линии могут добавлять элегантности и уютности окружающей среде.

В концептуальном искусстве эллипсы и овалы могут использоваться для передачи различных символических и смысловых значений. Некоторые художники используют эти формы, чтобы образно выразить круговорот времени, движение, переходы и прочие философские и метафорические идеи.

В искусстве эллипсы и овалы предоставляют множество возможностей для творчества и самовыражения. Они могут быть использованы для создания красивых и гармоничных композиций, а также для передачи символического и смыслового значения. Их органическая форма делает их привлекательными и универсальными для различных видов искусства.

Построение овалов и эллипсов

Казалось бы, а зачем их вообще строить?

Практически в любой технике имеются круглые детали — а они при переведении в трехмерную проекцию будут изображаться в форме замкнутых кривых. Подобные примеры можно приводить бесконечно.

Поэтому в технике, космонавтике, астрономии, архитектуре и многих других научных отраслях разнообразные овалы приходится строить регулярно. Эти знания применяют даже люди, далекие от сложных вычислений — например, художники.

Для того чтобы начертить любую из этих фигур, потребуется лишь циркуль, транспортир и линейка. Сам процесс особых сложностей не вызывает, главное внимательность и точность.

На фото ниже приведен пример построения эллипса в аксонометрии (изометрия).

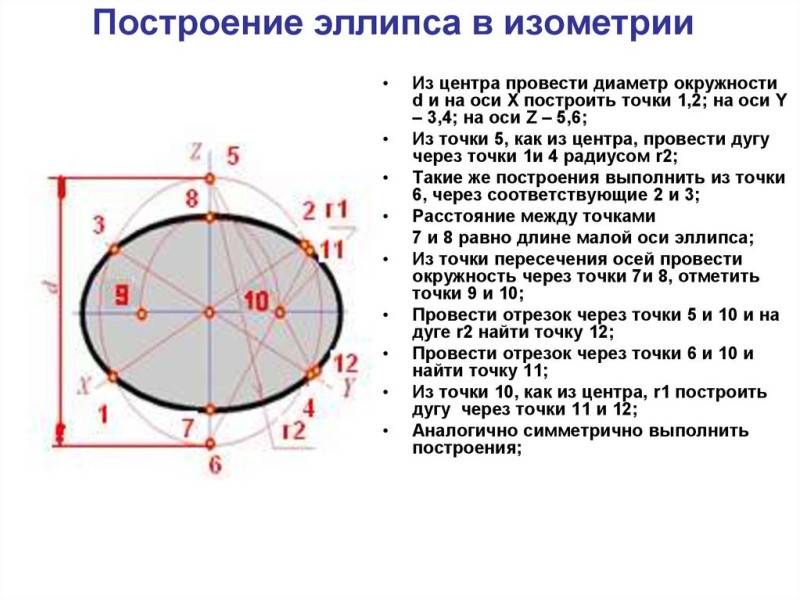
Для сравнения, в видео ниже показан пример построения овала:

Эллипс

Из основных характеристик эллипса следует упомянуть его уравнение. Алгоритм для определения уравнения эллипса основан на расстоянии от фокуса до точки кривой. Эллипс выделяется своими фокусами, точками на кривой, для которых сумма расстояний до фокусов постоянна.

Визуально эллипс может быть похож на овал, но между ними есть разница. Овал — это парабола с вытянутой осью, тогда как эллипс имеет две симметричные оси. Овал обычно более широкий и плавный, чем эллипс, поэтому эллипс часто считается более симметричной и уравновешенной формой.

Зная характеристики эллипса, можно проводить различные геометрические операции с ним. Например, построение линии, проходящей через фокусы эллипса, или нахождение пересечений с другими геометрическими фигурами.

Таким образом, эллипс является одной из важных геометрических фигур, имеющей свои особенности и характеристики. Разница между овалом и эллипсом заключается в их форме, симметрии и уравнении.

Основные характеристики эллипса

Эллипс можно назвать удлиненным овалом или овалом симметрии. Главная разница между эллипсом и овалом заключается в основной линии фигуры. У эллипса основная линия называется большой полуосью (а), а у овала это второстепенная линия.

Одна из основных характеристик эллипса — его эксцентриситет. Эксцентриситет эллипса определяет его плоскость, его форму. Чем ближе эксцентриситет к нулю, тем более круглым будет эллипс, а чем ближе к единице, тем более вытянутым будет эллипс.

Другая важная характеристика — фокусные точки эллипса. Фокусные точки это две точки внутри эллипса, для которых сумма расстояний до любой точки на эллипсе всегда одинакова. Если обозначить эти точки как F1 и F2, то для любой точки на эллипсе A, сумма расстояний AF1 и AF2 всегда будет одинаковой.

Эллипс также имеет основные оси. Большая полуось (а) является самой длинной линией эллипса, проходящей через его центр. Меньшая полуось (b) является самой короткой линией, перпендикулярной большой полуоси и проходящей через центр эллипса.

Важно отметить, что овал является частным случаем эллипса, когда его эксцентриситет равен единице

Название	Описание
Эксцентриситет	Определяет форму эллипса
Фокусные точки	Две точки внутри эллипса с одинаковой суммой расстояний до эллипса
Большая полуось	Самая длинная линия, проходящая через центр эллипса
Меньшая полуось	Самая короткая линия, перпендикулярная большой полуоси и проходящая через центр эллипса

Форма и структура эллипса

Главная разница между овалом и эллипсом заключается в том, что овал является формой, в которой все линии огибаются равными расстояниями от центра. В то же время, эллипс — это форма, в которой есть два фокуса, вокруг которых линии огибаются с разными расстояниями.

У эллипса есть математическое уравнение, известное как уравнение эллипса, которое определяет его форму и расположение на графике. Также существует алгоритм для рисования эллипса, который позволяет точно нарисовать его форму на основе его уравнения.

Таким образом, форма и структура эллипса имеют определенные особенности, отличающие его от овала

Это важно учитывать при рассмотрении и использовании этих геометрических фигур в различных областях науки и практики

Примеры использования эллипса

1. В архитектуре эллипсы часто используются для создания оригинальных форм зданий. Одним из известных примеров использования эллипса в архитектуре является стадион «Маракана» в Бразилии, где форма стадиона представляет собой эллипс.
2. В геодезии эллипсы используются для моделирования формы Земли и ее отклонений от сферы. Геоид — это эллипсоид, который представляет собой модель формы Земли, учитывающую ее геометрические отклонения и распределение массы.
3. В оптике эллипсы используются для описания формы линз и заземления света. Линзы с эллиптической формой позволяют менять фокусное расстояние и фокусировать световые лучи в разных точках.
4. В астрономии эллипсы используются для описания формы галактик. Галактики эллиптической формы имеют характерное эллиптическое распределение звезд и отличаются от спиральных галактик.

Таким образом, разница между овалом и эллипсом заключается в их характеристиках и использовании. Овал — это произвольная фигура без явно определенной формы, в то время как эллипс имеет строго определенные параметры и уравнение.

В чём отличие между эллипсом и овалом

В школе многим из нас неоднократно объясняли, в чём разница радиуса от диаметра, серной кислоты от соляной, эллипса от овала. Но прошли годы, и школьные знания, «слежавшись» под весом многолетней будничной рутины, в основном позабылись.

В рамках этой статьи мы попытаемся компенсировать хотя бы один неприятный пробел в знаниях и детальнее рассмотрим последний из приведённых примеров, обучившись отличать овал от эллипса. Для начала обозначим основные определения.

Под овалом в геометрии понимается вытянутая закрытая фигура правильной формы. Овал относится к двухмерным фигурам и обладает специальными качествами.

Окружность. Эллипс.

Само слово образовано от французского Ovale, которое, со своей стороны, имеет общие корни с латинской лексемой ovum, что в переводе значит «яйцо». Кривая этого геометрического объекта имеет с абсолютно любой прямой не больше 2-ух общих точек.

Конические сечения. Эллипс

Справка! Не скажешь, что человек, называющий данную фигуру геометрической формы просто «кругом», полностью прав.

В действительности окружность (в которой, как мы знаем, все точки кривой равноудалены от центра) – это одна из большинства вариантов овала.
Есть структурно очень сложное понятие овала в инженерной графике.

В данной сфере науки этим термином обозначают фигуру, которая имеет две оси симметрии и построенную с помощью комбинирования четырёх участков кривых линий от 2-ух радиусов. Данные участки выбраны поэтому, чтобы обеспечить «перетекание» от одного радиуса к иному без нарушения симметрии и контура фигуры.

Если определять координаты точки, регулярно двигающейся по линии овала, то она всегда будет располагаться на одном из описанных выше радиусов кривизны. Эти радиусы считаются «фиксированными».

Эллипс и его каноническое уравнение

Правописание… пожалуйста, не повторяйте ошибок некоторых пользователей Яндекса, которых интересует «как построить эллибз», «отличие элипса от овала» и «эксцентриситет элебса».

Каноническое уравнение эллипса имеет вид , где   – положительные действительные числа, причём . Само определение эллипса я сформулирую позже, а пока самое время отдохнуть от говорильни и решить распространённую задачу:

Как построить эллипс?

Да, вот взять его и просто начертить. Задание встречается часто, и значительная часть студентов не совсем грамотно справляются с чертежом:

Пример 1

Построить эллипс, заданный уравнением

Решение: сначала приведём уравнение к каноническому виду:

Зачем приводить? Одно из преимуществ канонического уравнения  заключается в том, что оно позволяет моментально определить вершины эллипса, которые находятся в точках . Легко заметить, что координаты каждой из этих точек удовлетворяют уравнению .

В данном случае :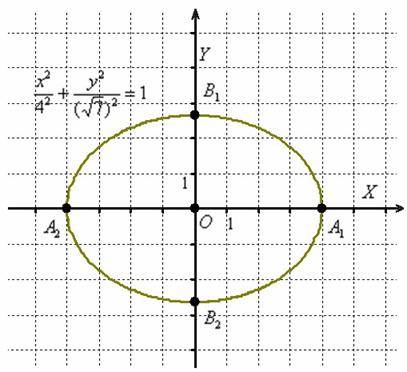Отрезок  называют большой осью эллипса;отрезок  – малой осью;число  называют большой полуосью эллипса; число  – малой полуосью.
в нашем примере: .

Чтобы быстро представить, как выглядит тот или иной эллипс достаточно посмотреть на значения «а» и «бэ» его канонического уравнения.

Всё ладно, складно и красиво, но есть один нюанс: я выполнил чертёж . И вы можете выполнить чертёж с помощью какого-либо приложения. Однако в суровой действительности на столе лежит клетчатый листок бумаги, и на наших руках водят хороводы мыши. Люди с художественным талантом, конечно, могут поспорить, но мыши есть и у вас тоже (правда, поменьше). Таки не зря человечество изобрело линейку, циркуль, транспортир и другие нехитрые приспособления для черчения.

По этой причине нам вряд ли удастся аккуратно начертить эллипс, зная одни вершины. Ещё куда ни шло, если эллипс небольшой, например, с полуосями . Как вариант, можно уменьшить масштаб и, соответственно, размеры чертежа. Но в общем случае крайне желательно найти дополнительные точки.

Существует два подхода к построению эллипса – геометрический и алгебраический. Построение с помощью циркуля и линейки мне не нравится по причине не самого короткого алгоритма и существенной загроможденности чертежа. В случае крайней необходимости, пожалуйста, обратитесь к учебнику, а в реальности же гораздо рациональнее воспользоваться средствами алгебры. Из уравнения эллипса  на черновике быстренько выражаем: 

Далее уравнение распадается на две функции: – определяет верхнюю дугу эллипса; – определяет нижнюю дугу эллипса.

Заданный каноническим уравнением эллипс симметричен относительно координатных осей, а также относительно начала координат. И это отлично – симметрия почти всегда предвестник халявы. Очевидно, что достаточно разобраться с 1-й координатной четвертью, поэтому нам потребуется функция . Напрашивается нахождение дополнительных точек с абсциссами . Настукаем три смс-ки на калькуляторе: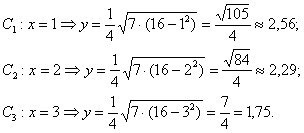
Безусловно, приятно и то, что если допущена серьёзная ошибка в вычислениях, то это сразу выяснится в ходе построения.

Отметим на чертеже точки  (красный цвет), симметричные точки на остальных дугах (синий цвет) и аккуратно соединим линией всю компанию: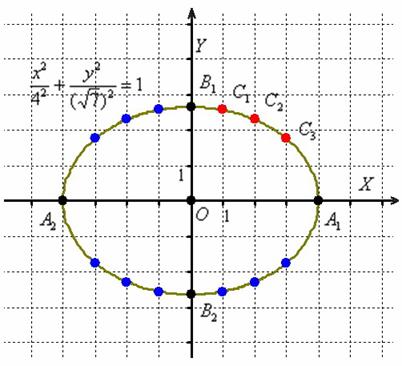
Первоначальный набросок лучше прочертить тонко-тонко, и только потом придать нажим карандашу. В результате должен получиться вполне достойный эллипс. Кстати, не желаете ли узнать, что это за кривая?

Расположение осей эллипса и овала

В овале, оси также являются перпендикулярными отрезками, но их расположение отличается от эллипса. Одна ось проходит через вершины овала, а другая ось — через его центр и перпендикулярна оси, проходящей через вершины. Таким образом, оси овала являются более смещенными по отношению друг к другу, что придает ему более вытянутую форму по сравнению с эллипсом.

Таким образом, расположение осей является одним из важных значений, которые помогают отличить эллипс от овала. Оно определяет форму и симметрию фигуры, что может быть полезным при ее классификации и создании графических картинок.

What is Circle?

A circle is a geometrical figure which is more of a round figure shape and is used to solve mathematical equations and problems. It is one of the most common and extensively used mathematical figures, which has its function in geometry.

A circle has a unique feature in that all the points in the circumference of a circle are at an equal distance to the centre. A circle is mostly classified by its shape and the distance from the centre.

The study of geometrical figures has helped over the development of maths and science over time, and the circle is one of such important figures among the others that has also contributed to the study of mathematics. 

A circle also has a definite formula to find its radius and other components that are important for the study of geometry. There are multiple examples of circular figures or objects, even in real life, other than mathematical figures.

The main principle with which the formation of a circle works is used in the process of creating circular objects in reality. 

These applications and principles are used in mathematics and real life to process these figures, such as the making of wheels in human life. 

Эллипс

У слова «эллипс» имеются греческие корни, самые близкие по переводу к словам «нехватка, минус, опущение». Чего же не хватает в эллипсе и что данная фигура вообще из себя представляет?

Эллипсом в большинстве случаев считают любую замкнутую кривую на плоскости, имеющую 4-ре вершины в называемых по другому точках экстремума. Точки фокуса эллипса равноудалены от его вершин.

Определить тип кривой (эллипс)

Стороны эллипса будут симметричны, если поделить его в любом направлении прямой, которая проходит через его центр. Тем не менее, данное правило на самом деле и для фигур округлого типа.

Проективная геометрия

К определению овала на проективной плоскости

К определению овоида

На проективной плоскости множество точек Ω называется овалом , если:

1. Любая прямая l пересекает Ω не более чем в двух точках, и
2. Для любой точки P ∈ Ω существует ровно одна касательная t, проходящая через P , т. Е. T ∩ Ω = { P }.

Для конечных плоскостей (т.е. множество точек конечно) существует более удобная характеристика:

Для конечной проективной плоскости порядка n (т. Е. Любая прямая содержит n + 1 точку) множество точек Ω является овалом тогда и только тогда, когда | Ω | = П + 1 , и никакие три точки не коллинеарны (на одной линии).

Яйцевидный в проективном пространстве множества Ω точек , таких , что:

1. Любая прямая пересекает Ω не более чем в 2 точках,
2. Касательные в точке покрывают гиперплоскость (и не более того), и
3. Ω не содержит прямых.

В конечном случае только для размерности 3 существуют овоиды. Удобная характеристика:

В 3-х комнатном. конечное проективное пространство порядка n > 2 любое точечное множество Ω является овоидом тогда и только тогда, когда | Ω | и никакие три точки не лежат на одной прямой.знак равноп2+1{\ displaystyle = n ^ {2} +1}

Гиперэллипс Ламе

Кривая показана на рис. 1б
. Такую форму и такое название кривая имеет, если степени m
и n
в формуле кривой Ламе больше 2.

Гиперэллипс, так же, как овал Кассини (который описан в ), имеет два основных оптических фокуса и три дополнительных. Само название его говорит о том, к какой группе следует отнести этот овал — к гиперовалам.

Гипоэллипс Ламе, показанный в , где он был назван просто кривой Ламе, в формуле имеет степени m
и n
меньше 2. При степенях m
и n
равных 2 кривая Ламе является эллипсом. В случае если одна из степеней больше, а другая меньше 2, мы имеем гипергипоэллипс (рисунок не показан). Если по полюсам этого овала построить эллипс, то можно увидеть, что кривые имеют как точки касания, так и точки пересечения между собой.