Ход занятия
1. Восп-ль показывает прямоугольник и квадрат
, прикреплённые к
магнитной доске, и спрашивает
: – Дети, как называются эти фигуры?
Вы уже научились узнавать прямоугольник и квадрат
. Сегодня мы выясним, чем они похожи и чем отличаются. Положите слева перед собой прямоугольник
, а справа – квадрат
. Давайте рассмотрим прямоугольник
: обведите его пальцем. – Что есть у прямоугольника
? Как узнать сколько сторон у прямоугольника
?Сосчитайте стороны. -Сколько у прямоугольника сторон
? Спрашиваю 3ребят, делаю обобщение
: – Правильно дети у прямоугольника 4 стороны
.
Дети а что ещё есть у прямоугольника
? Посмотрите, я покажу углы прямоугольника
, а вы их сосчитайте. Показываю углы, делая веерообразные движение от одной стороны до другой.
Дети, а теперь посчитайте углы своего прямоугольника
.
Сколько углов у прямоугольника
? – По скольку углов и сторон у прямоугольника
(ответы 2-3 детей)
Дети обведите рукой квадрат
. – Что есть у квадрата
?
Сколько сторон, – Сколько углов?
Дети, чем похожи квадрат и прямоугольник
? (ответы детей)
Правильно дети, у квадрата и прямоугольника
по 4 стороны и 4угла. Этим они похожи. Пальчиковая гимнастика
: «Белый мельник»
Дети, посмотрите одинакового ли размера стороны прямоугольника
?
Есть ли у них равные стороны? Сколько их?
Как доказать что противоположные стороны равны? Правильно, можно согнуть прямоугольник
по противоположным сторонам. Совпали они?да, стороны совпали, значит они равны!
Дети покажите две другие противоположные стороны! Докажите что они тоже равны! А смежные стороны равны или нет? (педагого проводит рукой по смежным сторонам)
. Как проверить? Правильно прямоугольник нужно согнуть так
, чтобы эти смежные стороны приложить друг к другу. (дети выполняют)
.
Равны ли эти стороны между собой? (они не равны)
Сколько же равных сторон у прямоугольника
(по 2 равных)
.
Как расположены эти стороны? (друг напротив друга)
Дети, а что можно сказать о размере сторон квадрата
?
Как проверить все ли стороны квадрата равны
? Верно можно сгибать квадрат
, прикладывая одну сторону к другой, и увидеть равны они. Проверьте равны ли стороны квадрата
.
Дети скажите, чем отличается квадрат от прямоугольника
?
Верно у квадрата все стороны равны
, а у прямоугольника
противоположные стороны равны.
А чем похожи похожи квадрат и прямоугольник
? (у квадрата у прямоугольника
по 4 угла и 4 стороны)
.
Что же мы узнали о квадрате и прямоугольнике
(у квадрата 4 угла и 4 стороны
, которые равны, у прямоугольника
4 угла и 4 стороны противоположные равны).
3. – Дети мы будем учиться идти в нужном направлении направлении и
Дети назовите предметы такой же формы.
5. Дети занятие у нас заканчивается поэтому давайте вспомним
С какими фигурами мы с вами познакомились?
Чем они похожи и чем различны?
Напечатать
Применение
Квадраты и прямоугольники находят применение в разных сферах нашей жизни:
- Архитектура и строительство: квадраты и прямоугольники используются при проектировании и строительстве зданий и сооружений, так как они являются одной из основных и наиболее стабильных геометрических форм.
- Дизайн и искусство: прямоугольники и квадраты могут служить основой для создания графических композиций, изображений и искусственных объектов.
- Математика: квадраты и прямоугольники активно используются при решении геометрических задач, расчетах площадей и периметров, а также в теории вероятностей и статистике.
- Информационные технологии: прямоугольники и квадраты могут быть использованы в веб-дизайне для создания различных элементов интерфейса, таких как кнопки, изображения или рамки.
- Образование: в школьной программе геометрии изучаются свойства и применение квадратов и прямоугольников, помогая развить понимание геометрических форм и умения решать задачи.
- Декорирование и интерьер: квадраты и прямоугольники могут использоваться для создания гармоничного интерьера, например при выборе плитки, обоев или мебели.
Таким образом, как квадраты, так и прямоугольники играют важную роль в различных сферах нашей жизни, обеспечивая стабильные и удобные геометрические формы для различных целей и задач.
Построение прямого угла, прямоугольника, квадрата на клетчатой бумаге
Как вы заметили, король Луч и принцесса Точка любят чертить. Они приглашают нас, ребята, поучаствовать в этом увлекательном занятии. Вооружитесь тетрадью в клеточку, простым карандашом, угольником.
Задание: построить на бумаге в клеточку прямой угол, прямоугольник со сторонами 6 см и 3 см, квадрат со стороной 7 см.
Посмотрите, как получилось у принцессы. Сравните со своими чертежами.
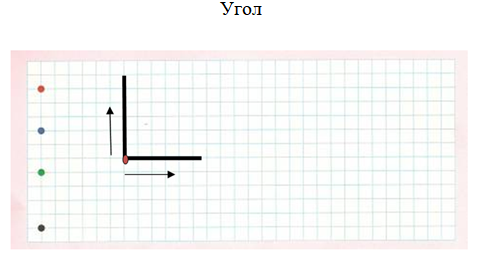
Ставим точку. Откладываем два луча при помощи угольника или линейки.
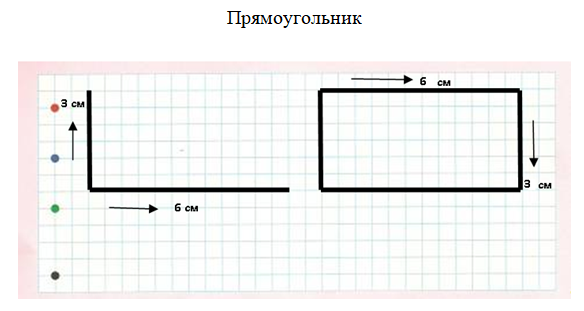
Ставим точку. Вверх – 3 см, вправо – 6 см. Помним, что противоположные прямоугольника стороны равны. Чертим их – 6 см и 3 см.
Квадрат
А это тетрадь короля. Он чертил квадрат. Сравните со своим чертежом.
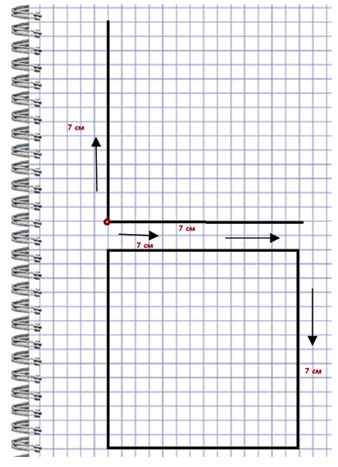
Ставим точку. Помним, что у квадрата все стороны равны. Откладываем вверх 7 см, вправо – 7 см. Чертим противоположные стороны по 7 см.
Молодцы, здорово получилось! Если такое занятие было для вас интересным и увлекательным, попробуйте начертить прямой угол, прямоугольник и квадрат на нелинованной бумаге. Сделать это будет гораздо сложнее. Здесь на помощь придет угольник: проверять прямой угол. Можно воспользоваться моделью прямого угла, которую мы изготовили.
Посмотрите, как это получилось у короля и Точки.
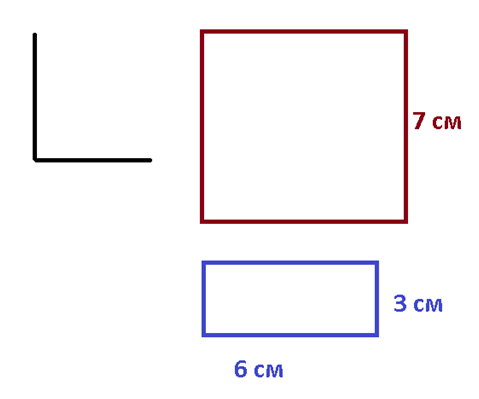
После нелегкого занятия король Луч и его дочка присели отдохнуть. Принцесса попросила рассказать интересную сказку. Давайте и мы послушаем!
Сказка
Жил-был на свете Прямоугольник. Фигура важная, спору нет! Люди ценили и уважали Прямоугольника, потому что при изготовлении многих вещей использовали эту фигуру. Всё хорошо у Прямоугольника, но одиноко как-то. Решил он найти своих родственников. Думает: «Если встречу родственников, сразу узнаю, потому что на меня должны быть похожи!».
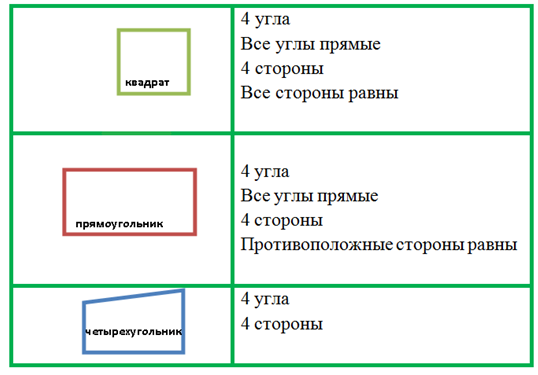
Однажды встретил Прямоугольник Квадрата и говорит: «Как тебя зовут? Очень ты, брат, на меня похож!». Отвечает Квадрат: «Если найдем не меньше четырех общих признака, значит, родственники». Стали они друг друга рассматривать и обнаружили четыре сходства:
У каждого было по 4 угла, да все прямые, по 4 стороны, да стороны, которые одна напротив другой – одинаковой длины.
Обрадовались родственники, что нашли друг друга. Поспешили вместе отправиться дальше. Встретили однажды Четырехугольника и спрашивают: «Похож ты на нас. Уж не родня ли?».
Говорит им Четырехугольник: «Я был бы очень рад! Если найдем хотя бы два сходства, значит, родственники». Стали опять внимательно друг к другу приглядываться и увидели два общих признака:
- 4 угла.
- 4 стороны.
Обрадовались фигуры и решили не терять друг друга, держаться всегда рядом.
Понравилась вам сказка? Давайте повторим о фигурах все, что узнали.
В сказочное королевство Геометрия мы вернемся еще не раз. А этот урок подошел к концу. Выберите смайлик вашего настроения.

До скорой встречи в королевстве Геометрия! А сейчас проверьте свои знания. Принцесса Точка справилась с заданиями хорошо, допустила одну небольшую ошибку. Будьте внимательны, не спешите!
Овал: геометрические характеристики
Овал — это плоская фигура, которая представляет собой замкнутую кривую линию, имеющую форму, близкую к эллипсу, но не являющуюся точно эллипсом. Овал имеет некоторые характеристические черты, которые позволяют его отличить от эллипса и других фигур.
Главные геометрические характеристики овала включают:
- Длина: это периметр овала — сумма всех сторон фигуры. Для регулярного овала (в котором все стороны и углы равны) длина может быть вычислена как произведение половины суммы большой и малой осей (a и b) на число пи (π).
- Площадь: это количество плоской площади, ограниченной овалом. Для регулярного овала площадь может быть вычислена как произведение половины большой оси (a) и половины малой оси (b) на число пи (π).
- Оси: овал имеет две оси — большую (a) и малую (b). Большая ось — это самая длинная прямая линия, проходящая через центр овала и образующая его длину. Малая ось — это прямая линия, перпендикулярная большой оси и образующая его ширину.
Кроме того, овал может иметь центр — точку, которая делит его на две равные части и находится в середине его большой и малой осей.
Вместе эти характеристики помогают определить форму овала и отличить его от других фигур, таких как круг или эллипс.
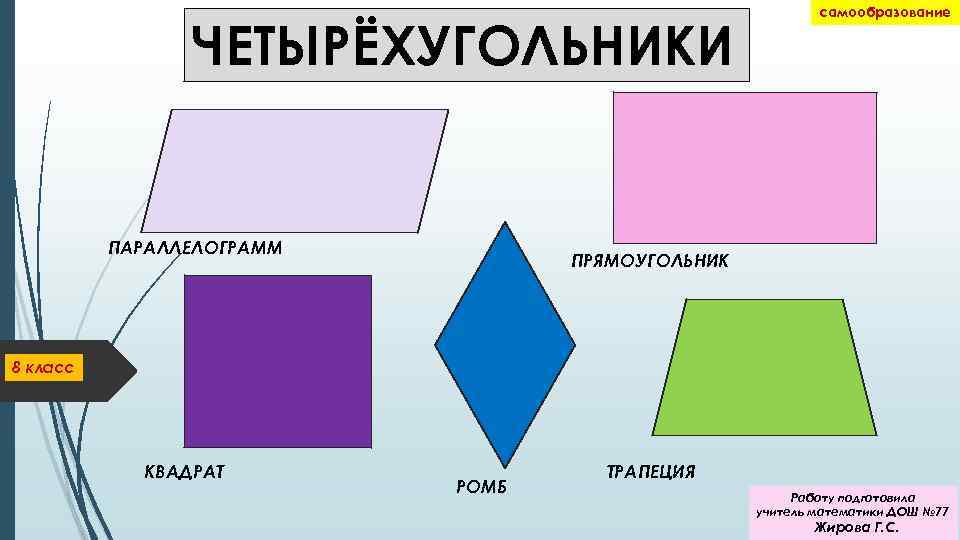
Свойства четырехугольников. Прямоугольник.
Свойства прямоугольника:
Пункт 1) совсем очевидный – ведь просто выполнен признак 3 ()
А пункт 2) – очень важный
. Итак, докажем, что
А значит, по двум катетам (и – общий).
Ну вот, раз треугольники и равны, то у них и гипотенузы и тоже равны.
Доказали, что!
И представь себе, равенство диагоналей – отличительное свойство именно прямоугольника среди всех параллелограммов. То есть верно такое утверждение^
Давай поймём, почему?
Значит, (имеются в виду углы параллелограмма). Но ещё раз вспомним, что – параллелограмм, и поэтому.
Значит, . Ну и, конечно, из этого следует, что каждый из них по! Ведь в сумме-то они должны давать!
Вот и доказали, что если у параллелограмма
вдруг (!) окажутся равные диагонали, то это точно прямоугольник
.
Но! Обрати внимание!
Речь идёт о параллелограммах
! Не любой
четырехугольник с равными диагоналями – прямоугольник, а только
параллелограмм!
Публикация «Конспект НОД по ФЭМП на тему „Квадрат и прямоугольник“» размещена в разделах
- Геометрические фигуры. Конспекты занятий по математике
- Квадрат. Геометрическая фигура
- Конспекты занятий. Все конспекты
- Математика. Конспекты занятий по ФЭМП
- Математика. Математические представления, ФЭМП
- Прямоугольник. Геометрическая фигура
- Темочки
- Конкурс для воспитателей и педагогов «Лучший конспект занятия (НОД)» август 2014
вательно обследовать форму предметов, упражнять в нахождении
фигур на ощупь.
(Форма которых соответствует знакомым детям геометрическим
образцам: квадрату, прямоугольнику, треугольнику, шару, цилиндру,
кубу).
Развивать память, внимание. Воспитывать желание познавать новое
Воспитывать желание познавать новое.
Демонстрационный материал: модели прямоугольника и квадрата из
бумаги, 6 игрушек разной формы.
Раздаточный материал: Модели квадрата и прямоугольника, но меньшего
размера. (в 1,5 раза демонстрационного)
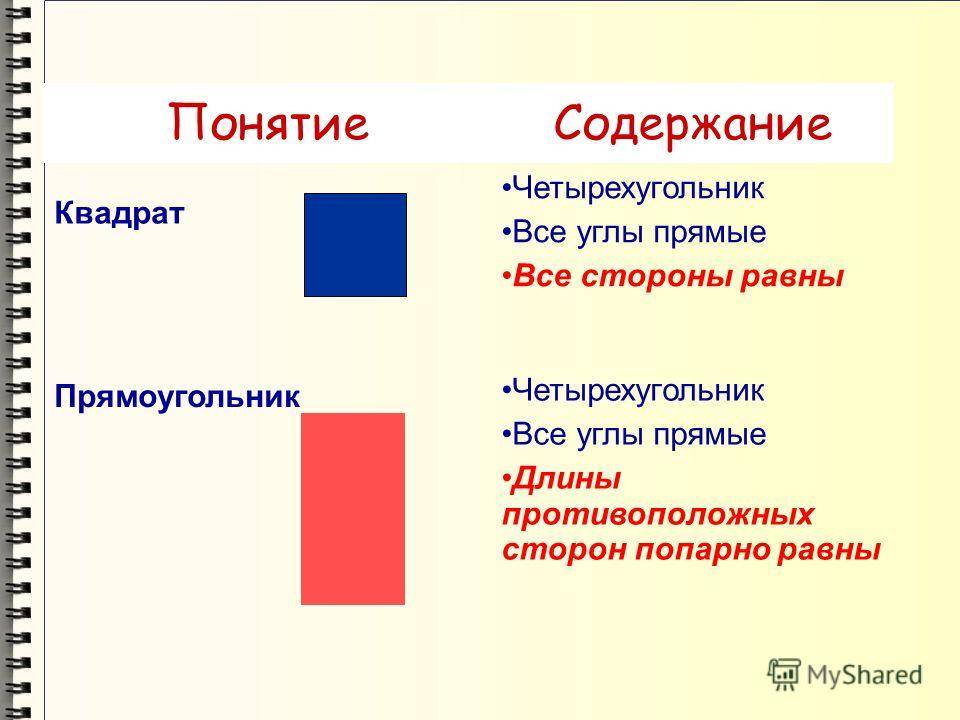
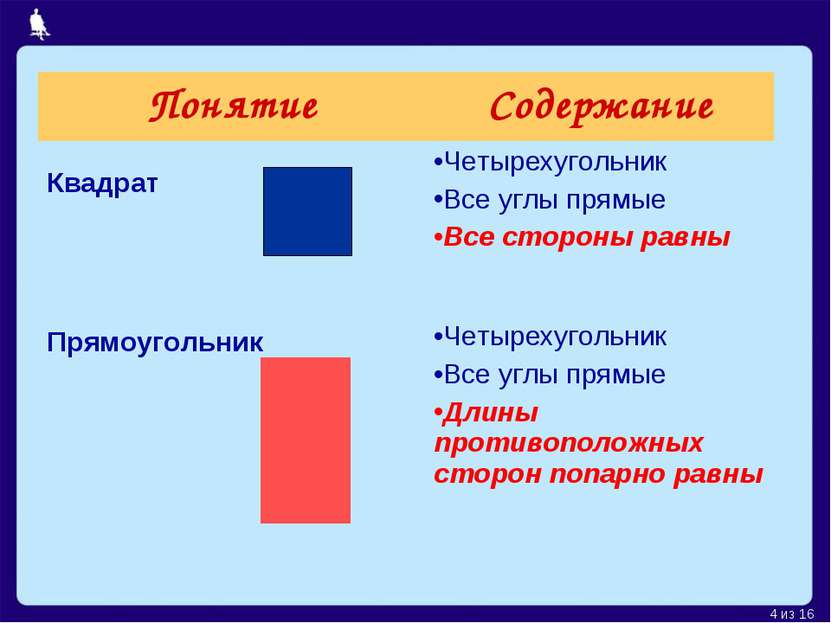
Различия между квадратом и прямоугольником
Квадрат и прямоугольник являются двумя различными геометрическими фигурами. Хотя оба имеют четыре стороны и углы, есть несколько ключевых различий между ними.
Форма: Квадрат имеет все стороны одинаковой длины, в то время как прямоугольник имеет пары противоположных сторон, которые могут иметь разную длину.
Углы: В квадрате все углы равны 90 градусам, в то время как в прямоугольнике также могут быть углы, отличные от 90 градусов.
Свойства: Квадрат является частным случаем прямоугольника, что означает, что все свойства прямоугольника, такие как периметр и площадь, также справедливы для квадрата. Однако квадрат также имеет свои собственные характеристики, такие как диагональ, которая является равной длине стороны, и радиус вписанной и описанной окружностей.
Использование: Квадраты могут использоваться в различных областях, например, в строительстве и дизайне, где требуется одинаковая длина всех сторон. Прямоугольники также находят широкое применение, например, в построении зданий и создании дизайна интерьера, где требуется задание разных длин сторон для получения определенного эффекта или функциональности.
Итак, хотя квадрат и прямоугольник являются схожими геометрическими фигурами с некоторыми общими характеристиками, их ключевые различия в форме, углах и использовании делают их уникальными и подходящими для разных задач.
А как насчет трехмерных геометрических фигур?
Существуют также трехмерные формы, которые имеют не только длину и ширину, но также глубину или объем. Это формы, которые вы видите в реальном мире, такие как сферический баскетбольный мяч, цилиндрический контейнер с овсянкой или прямоугольная книга.
Трехмерные формы, естественно, более сложные, чем двухмерные, с дополнительное измерение – количество места, которое они занимают, а не только форма, – которое необходимо учитывать при расчете площади и периметра.
Математика, включающая двумерные фигуры, подобные приведенным выше, называется плоская геометрия, потому что она имеет дело с плоскостями или плоскими формами. Математика, включающая трехмерные формы, такие как сферы и кубы, называется сплошная геометрия, потому что она имеет дело с твердыми телами, другим словом для трехмерных форм.
2D-формы составляют 3D-фигуры, которые мы видим каждый день!
Прямоугольник
Определение 3
Параллелограмм, у которого есть прямой угол, называется прямоугольником (рис. 1).
Рисунок 1. Прямоугольник
Очевидно, что в прямоугольнике все четыре угла равняются ${90}^0$
Рассмотрим два свойства прямоугольника.
Свойство 3: Обе диагонали прямоугольника равны между собой.
Доказательство.
Пусть нам дан прямоугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$ (рис. 2). Докажем, что $AC=BD$.
Рисунок 2.
Так как прямоугольник по определению $1$ является параллелограммом, то по свойству $1$ параллелограмма, имеем
Так как $\angle B=\angle A={90}^0$, а $AB$ – общая сторона, то по I признаку равенства треугольников, $\triangle ABD=\triangle ABC$. Следовательно
Свойство доказано.
Свойство 4 (признак прямоугольника): Если обе диагонали параллелограмма равны между собой, то он является прямоугольником.
Доказательство.
Пусть нам дан прямоугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $R$ (рис. 2).
Из свойства $2$ параллелограмма и равенства его диагоналей, получим
Так как $\angle DRC=\angle ARB$, как вертикальные, то по $I$ признаку равенства треугольников $\triangle DRC=\triangle ARB$. Значит, $\angle RDC=\angle RCD=\angle RAB={\rm \ }\angle RBA$.
Так как $\angle DRA=\angle CRB$, как вертикальные, то по I признаку равенства треугольников $\triangle DRA=\triangle CRB$. Значит, $\angle RDA=\angle RAD=\angle RCB={\rm \ }\angle RBC$.
Следовательно, $\angle A=\angle B=\angle C=\angle D$.
Так как сумма углов четырехугольника равняется ${360}^0$, то
Значит, по определению $3$, $ABCD$ является прямоугольником.
Свойство доказано.
Сравнение
Квадратом называют параллелограмм, у которого все четыре внутренних угла прямые. Все четыре стороны квадрата равны, то есть имеют одинаковую длину.
Прямоугольником называют параллелограмм, внутренние углы у которого прямые, и только противоположные стороны, которые параллельны друг другу, равны.
Для прямоугольника и квадрата характерны следующие свойства:
- все углы прямые;
- диагонали равны;
- в точке пересечения диагонали делятся пополам;
- противолежащие стороны параллельны друг другу и равны по длине.
Квадрат (прямоугольник)
Квадрат
(от лат. quadratus – четырёхугольный), 1) равносторонний прямоугольник. К. является правильным многоугольником
. 2) К. числа а –
произведение а
×а
= a
2
, название связано с тем, что именно таким произведением выражается площадь квадрата, сторона которого равна а
.
Большая советская энциклопедия. – М.: Советская энциклопедия
.
1969-1978
.
Смотреть что такое “Квадрат (прямоугольник)” в других словарях:
КВАДРАТ, в биологии квадратная рама, используемая для разметки участка поверхности с целью изучения растений, находящихся на нем. Квадратом называют также и сам этот участок почвы. Как правило, такой квадрат равен 0,5 или 1 м2. Пользуясь этим… … Научно-технический энциклопедический словарь
Прямоугольник
– : Смотри также: прямоугольник квадрат прямоугольник гладкая бочка … Энциклопедический словарь по металлургии
– (лат. quadratum, от quadrare сделать четырехугольным). 1) прямоугольный, равносторонний четырехугольник. 2) такое число, которое, будучи умножено само на себя, дает данное число. 3) единица для измерения плоскостей; напр.: квадратн. фут, дюйм и… … Словарь иностранных слов русского языка
Прямоугольник параллелограмм, у которого все углы прямые (равны 90 градусам). Примечание. В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые. Четвёртый угол (в силу … Википедия
Параллелограмм, четырехугольник, квадрат Словарь русских синонимов. прямоугольник сущ., кол во синонимов: 4 квадрат (9) … Словарь синонимов
Параллелограмм, клетка, материал, прямоугольник, степень, квадратик Словарь русских синонимов. квадрат сущ., кол во синонимов: 9 гиперкуб (12) … Словарь синонимов
КВАДРАТ, квадрата, муж. (лат. quadratus четырехугольный). 1. Равносторонний прямоугольник (мат.). 2. Форма такого прямоугольника у какого нибудь предмета (книжн.). Ярко освещенный квадрат окна. 3. Четырехугольный гартовый брусок мера для… … Толковый словарь Ушакова
– (от латинского quadratus четырехугольный), 1) равносторонний прямоугольник. 2) Вторая степень a2 числа a (название связано с тем, что именно так выражается площадь квадрата со стороной a) … Современная энциклопедия
– (от лат. quadratus четырехугольный) 1) прямоугольник с равными сторонами.2) Вторая степень числа (а), то есть а?а = а2 … Большой Энциклопедический словарь
КВАДРАТ, а, муж. 1. Равносторонний прямоугольник, а также предмет или участок такой формы. Квадраты на шахматной доске. Взлётный к. для вертолётов. 2. В математике: произведение числа на самого себя. Четыреэто к. двух. 3. В математике: показатель … Толковый словарь Ожегова
Книги
- Сфинкс. Магический квадрат. Гексатрион/ Игры-головоломки , . Собранные в этой книге игры имеют тысячелетнюю историю – склонность к геометрическим загадкам свойственна людям разных эпох и национальностей.
Разрезать простую геометрическую фигуру… - Аппликация в детском саду. Овощи, фрукты, грибы (набор из 16 карточек) , А. А. Грибовская. Аппликация – это вырезывание из бумаги “на глаз”, то есть без предварительной прорисовки. Это “рисование” ножницами, развивающее моторику пальцев, глазомер, чувства формы, пропорции, цвета.…
Галина Лахина
Конспект НОД по ФЭМП на тему «Квадрат и прямоугольник»
Цель
: учить детей различать квадрат и прямоугольник
, познакомить с
некоторыми характерными признаками этих фигур
: наличие углов,
сторон, их количеством, соотношением сторон по размеру
(у квадрата все стороны равны
, у прямоугольника только проти-
воположные стороны равны); учить последовательно выделять
и сравнивать однородные признаки фигур; учить передвигаться в
вательно обследовать форму предметов, упражнять в нахождении
фигур на ощупь.
(Форма которых соответствует знакомым детям геометрическим
образцам
: квадрату
, прямоугольнику
, треугольнику, шару, цилиндру,
Развивать память, внимание. Воспитывать желание познавать новое
Воспитывать желание познавать новое.
Демонстрационный материал
: модели прямоугольника и квадрата из
бумаги, 6 игрушек разной формы.
Раздаточный материал
: Модели квадрата и прямоугольника
, но меньшего
размера. (в 1,5 раза демонстрационного)
Углы квадрата и прямоугольника
Квадрат и прямоугольник — это две разные геометрические фигуры, имеющие свои особенности и различия. Одним из главных отличий этих фигур является количество углов.
Квадрат обладает четырьмя углами, которые все равны между собой и равны 90 градусам. Такие углы называются прямыми углами. Из-за равенства всех углов квадрат считается регулярным четырехугольником.
Прямоугольник, в свою очередь, имеет также четыре угла, но они не обязательно равны между собой. Углы прямоугольника могут быть как прямыми (равными 90 градусам), так и разными по величине. Зависит это от соотношения сторон прямоугольника.
Если противоположные стороны прямоугольника равны, то все его углы будут прямыми. В таком случае, прямоугольник также называется квадратом.
Однако, если противоположные стороны прямоугольника разной длины, то его углы также могут быть разными. Такой прямоугольник называется прямоугольником с прямыми углами, или просто прямоугольником, чтобы отличить его от квадрата.
| Фигура | Количество углов | Величина углов |
|---|---|---|
| Квадрат | 4 | 90 градусов |
| Прямоугольник | 4 | может быть разной |
Таким образом, углы квадрата и прямоугольника могут быть одинаковыми или разными в зависимости от их формы. Квадрат всегда имеет прямые углы, в то время как прямоугольник может иметь и прямые углы, и углы разной величины.
Эллипс: определение и свойства
Эллипс имеет две оси — большую и малую. Большая ось, также называемая длинной полуосью, проходит через два фокуса и центр эллипса. Малая ось, называемая короткой полуосью, проходит через центр и перпендикулярна большой оси.
Форма эллипса кажется симметричной относительно его центра, и его площадь может быть вычислена по формуле S = π а b, где а и b — длины полуосей.
Периметр эллипса также может быть вычислен с помощью формулы P ≈ 2π √(a² + b²/2), где а и b — длины полуосей.
Один из основных отличий эллипса от овала состоит в том, что все точки эллипса находятся на одинаковом расстоянии от двух фокусов, в то время как в овале эти расстояния могут отличаться.
Эллипс имеет ряд уникальных свойств и присутствует во многих аспектах природы, включая движение планет вокруг Солнца и форму некоторых облаков и камней.
Определение эллипса
У эллипса есть две оси — большая ось (a) и малая ось (b). Большая ось является длиннейшей прямой, проходящей через центр эллипса и соединяющей два противоположных вершины. Малая ось же проходит через центр эллипса, перпендикулярно к большей оси и соединяет два противоположных конца эллипса.
Длина большой оси равна двойному радиусу, так как радиус является половиной большой оси. Формула для определения длины большой оси эллипса — a = 2r.
Длина малой оси также равна двойному радиусу, поскольку радиус является половиной малой оси. Формула для определения длины малой оси эллипса — b = 2r.
Площадь эллипса можно вычислить с помощью формулы: S = π * a * b, где π — это число пи (приближенное значение 3,14159).
Периметр эллипса также может быть вычислен с помощью формулы: P = 2π * sqrt((a^2 + b^2)/2), где sqrt — квадратный корень, и ^ — значит возведение в степень.
Одно из отличий эллипса от овала заключается в том, что эллипс имеет симметричную форму, в то время как овал — неравномерный и несимметричный.
Эллипс является геометрической фигурой, которая встречается в природе, например, в форме орбит планет вокруг Солнца или в форме кометы при ее движении вокруг Солнца.
Математические свойства эллипса
Одной из важных характеристик эллипса является его форма. Форма эллипса может быть размерной или безразмерной. Размерная форма характеризуется показателем эксцентриситета, определяющего степень сжатия или растяжения эллипса. Безразмерная форма характеризуется отношением длины большой оси к длине малой оси, называемым аспектом.
Площадь эллипса вычисляется по формуле S = π * a * b, где a и b — полуоси эллипса. Периметр эллипса вычисляется по формуле P = 4 * а * E(1 — e^2), где Е — числовой эксцентриситет эллипса.
Эллипс имеет две оси — большую (а) и малую (b). Оси эллипса являются симметричными относительно центра. Длина большой оси обозначается как 2a, а длина малой оси — как 2b. Расстояние от центра эллипса до фокуса (f1 и f2) называется фокусным радиусом.
Эллипс имеет следующие математические свойства:
- Сумма расстояний от любой точки эллипса до фокусов равна длине большой оси.
- Произведение расстояний от любой точки эллипса до фокусов равно площади эллипса.
- Расстояние от центра эллипса до любой точки на эллипсе равно радиус-вектору этой точки.
- Эллипс — кривая второго порядка, которую можно задать уравнением вида (x^2/a^2) + (y^2/b^2) = 1, где x и y — координаты точки на эллипсе.
Эти свойства позволяют различать эллипс от других фигур и использовать его в различных областях математики и природных наук.
Что такое форма?
Если кто-то спросит вас, что такое форма, вы, вероятно, сможете назвать довольно много из них. Но у “формы” тоже есть особое значение.- это не просто названия кругов, квадратов и треугольников.
Форма – это форма объекта, а не то, сколько места он занимает или где находится физически, а реальная форма, которую он принимает. Круг определяется не тем, сколько места он занимает или где вы его видите, а скорее реальной круглой формой, которую он принимает.
Форма может быть любого размера и появляться где угодно; они ничем не ограничены, потому что фактически не занимают места. Трудно осознать это, но не думайте о них как о физических объектах – форма может быть трехмерной и занимать физическое пространство, например подставку для книг в форме пирамиды, цилиндрическую банку с овсянкой или он может быть двухмерным и не занимать физического места, например треугольник, нарисованный на листе бумаги.
Тот факт, что он имеет форму, отличает форму от точки или линии.
Точка – это просто позиция; у него нет ни размера, ни ширины, ни длины, ни вообще никаких размеров.
Линия же одномерная. Он бесконечно тянется в любом направлении и не имеет толщины. Это не форма, потому что у нее нет формы.
Хотя мы можем представлять точки или линии как фигуры, потому что нам действительно нужно их видеть, на самом деле они не имеют никакой формы. Вот что отличает форму от других геометрических фигур – она двух- или трехмерная, потому что имеет форму.
Кубики, подобные тем, что мы видим здесь, представляют собой трехмерные квадраты – обе формы!
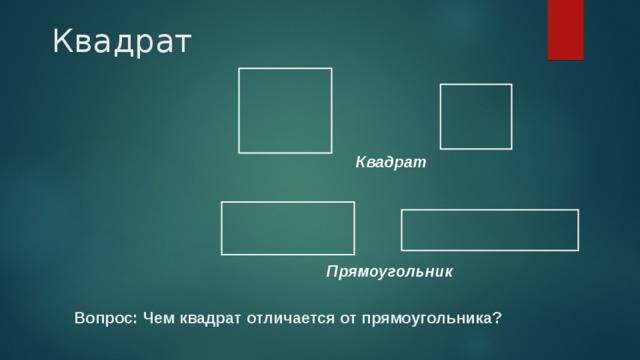
Квадрат и прямоугольник: различия и сходства
Квадрат и прямоугольник — это две геометрические фигуры, которые имеют некоторые сходства, но в то же время имеют и ряд различий.
Сходства:
- Квадрат и прямоугольник оба принадлежат к классу прямоугольников, то есть имеют четыре угла и все их стороны прямые.
- Обе фигуры могут быть описаны с помощью формулы периметра: P = 2a + 2b, где a и b — длины сторон.
- Также квадрат и прямоугольник обладают свойством параллельности противоположных сторон.
Различия:
- Форма: Основное различие между квадратом и прямоугольником заключается в их форме. Квадрат имеет все стороны одинаковой длины, а прямоугольник имеет две пары равных сторон. Таким образом, все углы квадрата равны 90°, в то время как углы прямоугольника могут быть разными.
- Стороны: Квадрат имеет все стороны одинаковой длины, в то время как прямоугольник может иметь различные длины сторон.
- Площадь: Формула для расчета площади квадрата: S = a*a, где a — длина стороны. Формула для расчета площади прямоугольника: S = a*b, где a и b — длины сторон.
Таким образом, квадрат и прямоугольник являются связанными фигурами, однако имеют некоторые важные различия, связанные с их формой, сторонами и площадью.
Занятие по ФЭМП в детском саду в старшей группе. Тема: Сравнение квадрата и прямоугольника
Демонстрационный материал: пять квадратов, пять прямоугольников.
Раздаточный материал: листы бумаги, набор «Учимся считать».
Ход занятия
1. Сравнение квадрата и прямоугольника.
В верхнем ряду наборного полотна помещают 4 прямоугольника, а в нижнем – 4 квадрата и 1 прямоугольник. (Фигуры каждого ряда разного цвета и размера.)
Воспитатель, указывая на наборное полотно, говорит детям:
– Ребята, я попросила Незнайку в верхнем ряду поместить 4 прямоугольника, а в нижнем 5 квадратов. Незнайка сделал вот так. Правильно ли он выполнил задание? В чем его ошибка?
Воспитатель предлагает детям объяснить Незнайке, чем похожи и чем отличаются квадрат и прямоугольник.
– Покажите стороны квадрата.
– Сколько сторон у квадрата?
– Равны ли они по длине?
То же с квадратом и прямоугольником.
– Сколько надо было взять квадратов?
– А прямоугольников?
– Каких фигур должно быть больше?
– Почему?
Дети называют ошибку Незнайки.
2. Гимнастика для глаз «Часовщик» (фрагмент из стихотворения «Веселая азбука про все на свете» С. Маршака).
Часовщик, прищурив глаз
(закрыть один глаз),
Чинит часики для нас
(закрыть другой глаз; открыть глаза).
3. Работа с раздаточным материалом.
Воспитатель:
– Сегодня мы будем учиться запоминать, сколько фигур и где надо положить, и сами себя проверять.
Задание: положите 4 круга в нижний правый угол листа, а 5 овалов вдоль левого края листа.
Затем одному-двум детям воспитатель предлагает повторить задание.
После этого на доску вывешивается образец. Дети проверяют, как они выполнили задание.
Один-два ребенка рассказывают, сколько каких фигур и где они положили.
Можно дать еще одно-два аналогичных задания.
Физкультминутка
Зайчикам не будет скучно,
Сделаем зарядку дружно?
Вправо, влево повернись,
Наклонись и поднимись.
Лапки кверху, лапки в бок
И на месте скок, скок, скок.
А теперь бежим вприпрыжку.
Молодцы, мои зайчишки!
Замедляем, детки, шаг,
Шаг на месте, стой!
Вот так.
4. Игра «Что изменилось?».
Дети образуют круг. Внутри него 4-5 человек. С помощью считалки выбирается ведущий.
Раз, два, три, четыре, пять,
Вышел зайчик погулять.
Что нам делать, как нам быть?
Надо зайчика ловить!
Снова будем мы считать:
Раз, два, три, четыре, пять!
Запомнив, как стоят дети, ведущий выходит из круга и отворачивается. Дети перестраиваются.
По сигналу ведущий входит в круг и определяет, какие изменения произошли: сколько человек ушло, сколько осталось, кто из детей поменялся местами и т. д.
5. Игра «Что похоже на квадрат (прямоугольник)?».
6. Логическая задача.
Катя живёт на третьем этаже. Квартира Оли находится над квартирой Кати. На каком этаже живёт Оля?
Ход занятия
1. Восп-ль показывает прямоугольник и квадрат, прикреплённые к
магнитной доске, и спрашивает: – Дети, как называются эти фигуры?
Вы уже научились узнавать прямоугольник и квадрат. Сегодня мы выясним, чем они похожи и чем отличаются. Положите слева перед собой прямоугольник, а справа – квадрат. Давайте рассмотрим прямоугольник : обведите его пальцем. – Что есть у прямоугольника? Как узнать сколько сторон у прямоугольника?Сосчитайте стороны. -Сколько у прямоугольника сторон? Спрашиваю 3ребят, делаю обобщение: – Правильно дети у прямоугольника 4 стороны.
– Дети а что ещё есть у прямоугольника? Посмотрите, я покажу углы прямоугольника, а вы их сосчитайте. Показываю углы, делая веерообразные движение от одной стороны до другой.
– Дети, а теперь посчитайте углы своего прямоугольника.
– Сколько углов у прямоугольника? – По скольку углов и сторон у прямоугольника (ответы 2-3 детей)
– Дети обведите рукой квадрат. – Что есть у квадрата?
– Сколько сторон, – Сколько углов?
– Дети, чем похожи квадрат и прямоугольник? (ответы детей)
– Правильно дети, у квадрата и прямоугольника по 4 стороны и 4угла. Этим они похожи. Пальчиковая гимнастика: «Белый мельник»
– Дети, посмотрите одинакового ли размера стороны прямоугольника?
– Есть ли у них равные стороны? Сколько их?
– Как доказать что противоположные стороны равны? Правильно, можно согнуть прямоугольник по противоположным сторонам. Совпали они?да, стороны совпали, значит они равны!
– Дети покажите две другие противоположные стороны! Докажите что они тоже равны! А смежные стороны равны или нет? (педагого проводит рукой по смежным сторонам). Как проверить? Правильно прямоугольник нужно согнуть так, чтобы эти смежные стороны приложить друг к другу. (дети выполняют).
– Равны ли эти стороны между собой? (они не равны)
– Сколько же равных сторон у прямоугольника (по 2 равных).
– Как расположены эти стороны? (друг напротив друга)
– Дети, а что можно сказать о размере сторон квадрата?
– Как проверить все ли стороны квадрата равны? Верно можно сгибать квадрат, прикладывая одну сторону к другой, и увидеть равны они. Проверьте равны ли стороны квадрата.
– Дети скажите, чем отличается квадрат от прямоугольника?
Верно у квадрата все стороны равны, а у прямоугольника противоположные стороны равны.
– А чем похожи похожи квадрат и прямоугольник? (у квадрата у прямоугольника по 4 угла и 4 стороны).
– Что же мы узнали о квадрате и прямоугольнике (у квадрата 4 угла и 4 стороны, которые равны, у прямоугольника 4 угла и 4 стороны противоположные равны).
3. – Дети мы будем учиться идти в нужном направлении направлении и
считать шаги. 4. Поиграем в игру «Чудесный мешочек». Я буду вас вызывать, а вы будете находить на ощупь.
– Дети назовите предметы такой же формы.
5. Дети занятие у нас заканчивается поэтому давайте вспомним
С какими фигурами мы с вами познакомились?
Чем они похожи и чем различны?
Что такое площадь?
Квадрат имеет определение объекта или плоскости, которая имеет все четыре стороны равной длины, и все углы, связанные с сторонами, также одинаковы. Некоторые из основных характеристик квадрата включают плоскую форму и тот факт, что он существует только в одной плоскости и имеет четыре точки, определяющие форму. Все стороны имеют одинаковую длину, как указано ранее, и размер этих длин может быть от 1 до выше при любом измерении. В то же время все углы имеют одинаковую длину, но основное отличие здесь заключается в том, что все четыре угла должны быть углами в 90 градусов, все, кроме этого, не сделает его квадратным, а форма может измениться на другие, такие как прямоугольник или даже треугольник. Процесс определения длины такого объекта прост, когда мы просто умножаем длину на ширину, поскольку все они имеют одинаковое значение. Другой способ взглянуть на измерение – это четыре равные стороны, то есть просто взять две стороны и найти квадрат из них, чтобы получить ответ. Поиск параметра такого значения может стать еще более простой задачей, вам просто нужно сложить все четыре длины, или даже просто, просто взять одну длину и умножить ее на четыре. Если мы видим квадрат в трехмерном пространстве, то квадрат становится кубом, и теперь у него намного больше сторон, чем шесть, что дает другое значение.