Чем отличается куб от квадрата

Вопрос-ответ:

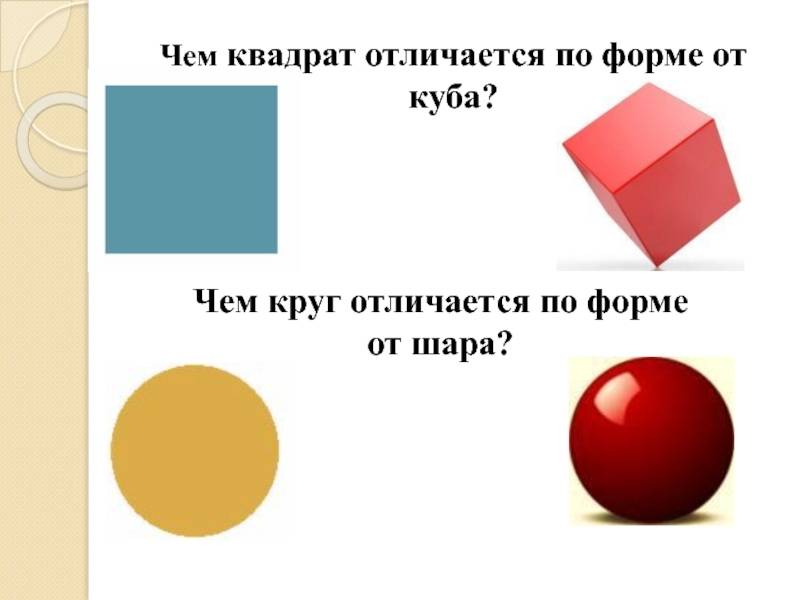
Чем отличается квадрат от куба?

Основное отличие между квадратом и кубом заключается в их размерности. Квадрат — это двумерная фигура, которая имеет только длину и ширину, в то время как куб — это трехмерная фигура, которая имеет длину, ширину и высоту. Кроме того, куб имеет более сложную структуру, состоящую из шести квадратных граней.

Какие у квадрата и куба свойства?

У квадрата и куба есть некоторые общие свойства. Оба могут быть описаны с помощью геометрических формул для вычисления площади, объема и периметра. Например, площадь квадрата равна квадрату длины его стороны, а объем куба равен кубу длины его ребра. Однако, из-за различной размерности у них все же есть много отличий.

Какие примеры можно привести для квадрата и куба?

Примеры квадрата могут включать листы бумаги, квадратные плитки, рамки на фотографии и многое другое. Кубом могут быть, например, кубические комнаты, кубики для игры, некоторые виды упаковок и так далее. В обоих случаях, форма и размерность отличаются, что приводит к их разным свойствам и применению.

Как квадрат и куб используются в математике?

В математике, квадрат часто используется для изучения геометрии, арифметических последовательностей и различных формул, таких как теорема Пифагора и формула для вычисления площади. Куб, с другой стороны, используется для изучения объема, трехмерной геометрии и различных формул, связанных с трехмерными фигурами. Оба могут быть использованы для решения задач и примеров в математике.

Как можно найти периметр квадрата и объем куба?

Периметр квадрата можно найти, умножив длину одной его стороны на 4. Объем куба можно найти, возводя в куб длину его ребра. Например, если длина ребра куба составляет 5 сантиметров, то его объем будет равен 5 * 5 * 5 = 125 кубических сантиметров.

Какие основные отличия между кубом и квадратом?

Квадрат — это геометрическая фигура, которая имеет четыре стороны одинаковой длины и четыре угла в 90 градусов каждый. Куб — это трехмерное тело, которое имеет шесть квадратных граней. Основное отличие между кубом и квадратом заключается в том, что куб имеет объем, в то время как квадрат имеет только площадь.

Количество сторон

Одно из главных отличий между кубом и квадратом в математике заключается в их количестве сторон. Квадрат имеет четыре стороны, которые образуют прямоугольник. Длины всех четырех сторон квадрата равны между собой.

В свою очередь, куб — это трехмерная фигура, которая имеет шесть сторон. Каждая сторона куба является квадратом, и все стороны имеют равную длину. Таким образом, куб состоит из шести квадратных граней, примыкающих друг к другу.

Квадрат	Куб
Имеет 4 стороны	Имеет 6 сторон
Стороны равны между собой	Стороны равны между собой
Является плоской фигурой	Является трехмерной фигурой

Таким образом, количество сторон является важной характеристикой, которая отличает куб от квадрата в математике. Квадрат имеет 4 стороны, в то время как куб имеет 6 сторон

Области применения

1. Геометрия: куб используется для изучения трехмерных пространств и решения задач геометрии, таких как вычисление объема, нахождение площади поверхности и определение диагоналей.

2. Архитектура: кубы и их пространственные комбинации широко применяются в архитектуре для создания моделей зданий, планирования помещений и анализа пространственных композиций.

3. Механика: в инженерных расчетах кубы используются для моделирования и анализа механических конструкций, таких как корпуса машин, каркасы и различные детали.

4. Кристаллография: в исследованиях кристаллической структуры вещества кубы являются одним из основных элементов для описания и классификации кристаллических решеток.

5. Визуализация данных: куб используется для представления трехмерной информации и обработки данных с помощью графических программ и специализированных систем.

Квадрат — двумерная фигура с четырьмя равными сторонами и четырьмя прямыми углами. Он также имеет свои области применения:

1. Геометрия: квадрат используется для изучения плоскостных фигур, нахождения площади и периметра, решения задач геометрии.

2. Математические модели: квадрат часто встречается в математических моделях и уравнениях, таких как квадратные уравнения.

3. Искусство и дизайн: квадрат используется в создании композиций, дизайна, архитектуры и является одним из основных элементов геометрической эстетики.

4. Логика и алгоритмы: квадраты могут быть использованы в логических схемах и алгоритмах для представления и обработки информации.

Итак, хотя куб и квадрат являются геометрическими фигурами, они имеют разные размерности и находят свое применение в разных сферах знаний и областях деятельности.

Чем отличается квадрат от куба?

Квадрат — это фигура геометрической формы, разместившаяся на плоскости (говоря иначе плоское отображение куба).

Куб — это объёмное тело (имеет грани).
По существу, все то же самое, если не предусматривать подобное понятие, как “объём”.

Квадрат это фигура на плоскости, ее можно изобразить прямоугольником с равными сторонами; куб это трехмерная фигура, у нее имеются 12 граней, смотрится в форме 6 квадратов; вообразите, что 2 находятся под углом 90 гр а 2 другие тоже под 90 и, если они соединяются, чтобы углы были прямые, выйдет фигура, и если к ней добавить основания, то мы сделаем куб

Квадрат это фигура плоская, на плоскости и лежащая. Имеющая 4-ре стороны одинаковой длины.

Куб же, фигура объёмная.

Кассета или трещотка. Что выбрать?

У которого сторон(которых у квадрата одна), будет шесть(попробуйте вспомнить кубик для игры в кости-шесть сторон от единички до шестёрки)
У квадрата одна сторона и 4-ре грани

У куба шесть сторон и двенадцать граней.
квадрат — это фигура с 4 похожими сторонами в плоскости
куб- фигура с 12 ребрами равной длины в трехмерном пространстве

Квадрат — фигура на плоскости.
Куб — трехмерный объект, в приватных случаях проекцией будет изображение квадрата.

Квадрат — это плоский объект

Разумеется нагляднее это взглянуть на моделях
Куб это объёмная фигура а квадрат лежит в одной плскости.

Квадрат — это плоская фигура с четырьмя вершинами и четырьмя похожими сторонами между этими вершинами.
Куб — трехмерная фигура с 8 вершинами и 12 похожими ребрами.

Фигура должна смотреться как традиционный детский кубик.

Квадрат и куб суммы и разности

А каждая приклеенная на кубика картинка имеет форму квадрата.
Если число (или какая-либо величина) строится к квадрат, то оно умножается на само себя.

Если в куб, то умножается само на себя и то что выйдет умножают на исходную величину ещё один раз.

Квадратами измеряют площадь, а кубами — объём.

Площадь и объем

Квадрат и куб — это геометрические фигуры, которые часто встречаются в математике и геометрии. Несмотря на то, что оба этих термина относятся к разным геометрическим фигурам, они имеют общую характеристику — это их размерность.

Квадрат — это плоская геометрическая фигура со сторонами, равными друг другу и прямыми углами. Площадь квадрата равна квадрату длины его стороны.

Куб — это трехмерная геометрическая фигура, которая имеет шесть квадратных граней. В отличие от квадрата, у куба есть еще третья размерность — высота. Объем куба равен кубу длины его стороны.

Таким образом, квадрат и куб отличаются друг от друга не только внешним видом и количеством размерностей, но и способом вычисления их площади и объема. Квадрат имеет только две размерности — длина стороны, а куб имеет три размерности — длина стороны, ширина и высота.

Квадрат

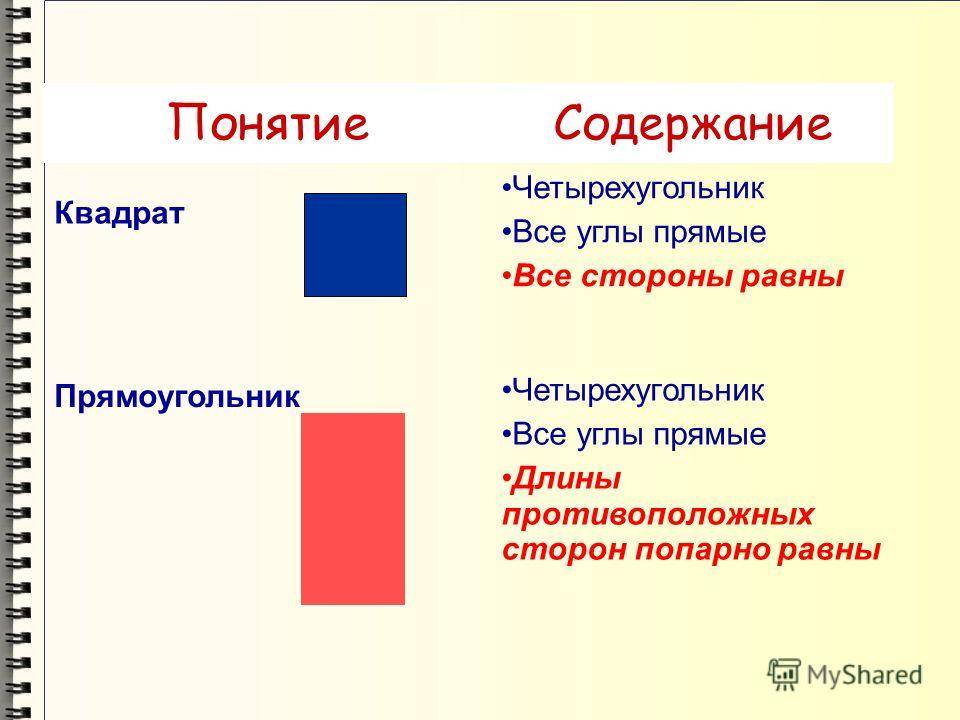
Квадрат — это геометрическая фигура, имеющая четыре равные стороны и четыре прямых угла. Квадрат является особой формой прямоугольника, где все стороны равны друг другу. Он также является частным случаем ромба, когда все углы прямые.

Квадрат отличается от куба своей размерностью. Куб, в отличие от квадрата, представляет собой трехмерную фигуру и имеет три размерных характеристики: длину, ширину и высоту. Куб состоит из шести граней, которые являются квадратами.

Квадрат и куб также отличаются своими свойствами. У квадрата есть только площадь, которая равна квадрату его стороны. У куба, кроме площади граней, есть еще и объем, который определяется как произведение стороны на сторону на сторону.

Куб

Куб — это геометрическое тело, которое имеет особые свойства и отличается от квадрата. В отличие от квадрата, который представляет собой плоскую фигуру с четырьмя равными сторонами, куб имеет объемную форму с шестью равными гранями.

Куб является трехмерным объектом и обладает свойством равенства всех его граней, ребер и углов. Каждая грань куба является квадратом, поэтому можно сказать, что куб состоит из шести квадратов. Это отличает его от квадрата, который имеет только одну грань.

Одно из главных отличий между кубом и квадратом — это измерение. Квадрат имеет только две измерения: длину и ширину, в то время как куб имеет три измерения: длину, ширину и высоту. Это позволяет кубу занимать пространство, в то время как квадрат остается на плоскости.

Куб также обладает особыми свойствами, связанными с его объемом и площадью поверхности. Объем куба вычисляется по формуле a³, где «a» является длиной его ребра. Площадь поверхности куба вычисляется по формуле 6a², где «a» — это длина ребра. В отличии от квадрата, у которого есть только площадь поверхности, у куба есть и объем.

Таким образом, куб и квадрат имеют несколько отличий. Куб является объемной фигурой с шестью равными гранями, в то время как квадрат — это плоская фигура с четырьмя равными сторонами. Куб имеет три измерения и может занимать пространство, в отличие от квадрата, который остается на плоскости. Кроме того, куб обладает объемом и площадью поверхности, в то время как квадрат имеет только площадь.

Square vs Cube

The difference between a square and a cube is that a square is a two-dimensional shape that is made of four equal lines. On the other hand, a cube is known to be a three-dimensional shape that includes 12 edges or lines. A square is a simple structure to design, while drawing a cube can be tricky for some people.

A Square is a type of shape that has four sides of the same length. Each angle of a square is a right angle.

Right angles are those that evaluate to 90 degrees. Square belongs to the quadratic polynomials. A square is considered to be a 2D shape that lacks depth.

It has four vertices and four edges, which is very important in mathematics, especially in geometry.

A cube is a solid shape that comprises six squares, and it is considered to be a 3D shape. It is a three-dimensional shape that has 12 edges and eight vertices.

To find out the volume of a cube, a person has to know measurements of only one side. ‘length x width x height = volume’ is the formula to figure out the volume.

Применение в реальной жизни

Квадраты и кубы играют значительную роль во многих аспектах нашей жизни. Рассмотрим некоторые примеры:

Архитектура: Квадраты и кубы используются в архитектуре для создания фундаментов, стен и других конструкций, которые обеспечивают прочность и стабильность зданий.
Геометрия: Квадраты и кубы используются для изучения геометрии, определения площадей и объемов фигур, а также для решения различных задач с использованием теорем Пифагора и Пифагора для прямоугольного треугольника.
Кубические уравнения: Кубические уравнения широко используются в математике, физике и инженерных науках для моделирования сложных систем и решения сложных задач.
Кристаллография: Кристаллография изучает структуру и свойства кристаллов, которые часто имеют форму кубиков или других регулярных геометрических фигур.
Технологические приложения: Кубические формы и геометрия широко используются в различных технологических процессах, таких как проектирование компьютерных чипов, создание моделей в компьютерной графике и создание 3D-принтеров.

Это лишь некоторые примеры применения кубов и квадратов в реальной жизни. Их использование распространено во многих областях и часто является неотъемлемой частью нашей повседневной жизни.

Форма и размер

Квадрат и куб — это геометрические фигуры, которые имеют некоторые схожие и различные характеристики. Одно из основных отличий между ними заключается в их форме и размере.

Квадрат — это двумерная фигура, все стороны которой равны между собой. У квадрата все углы также равны 90 градусов. В результате, все четыре стороны квадрата имеют одинаковую длину.

Куб, в свою очередь, является трехмерной фигурой. Он образован шестью квадратными гранями, которые соединены в точках попарно. У куба все ребра также равны между собой и образуют прямые углы.

Квадрат и куб отличаются друг от друга не только формой, но и размером. Квадрат может иметь различные размеры, в зависимости от длины сторон, тогда как куб обладает объемом и, следовательно, имеет три размера: длину, ширину и высоту. Куб также имеет больший объем, чем квадрат, поскольку он обладает третьей размерностью.

Квадрат

Квадрат – это геометрическая фигура, которая состоит из четырех сторон одинаковой длины и углов, равных 90 градусов. Квадрат отличается от куба тем, что это двумерная плоская фигура, в то время как куб имеет три измерения – ширину, высоту и глубину.

У квадрата все стороны равны и его периметр можно вычислить, умножив длину одной стороны на 4. В то же время, куб имеет 12 ребер и кажется объемным, благодаря третьей оси глубины.

В отличие от куба, квадрат не имеет объема и его площадь равна квадрату длины одной из его сторон. Квадраты широко используются в мире геометрии и математики, а также в строительстве и дизайне, где они являются основным элементом для создания прямоугольных форм и конструкций.

Куб

Куб — это трехмерная геометрическая фигура, которая имеет все стороны равными между собой и прямые углы на каждом из своих 6 граней. Куб является частным случаем параллелепипеда, в котором все стороны равны.

Одной из основных характеристик куба является его объем. Объем куба можно вычислить, возведя в куб длину его стороны. Для этого используется формула: V = a³, где V обозначает объем куба, а a — длину его стороны.

Куб также отличается от квадрата количеством граней. В то время как у квадрата 4 грани, у куба их число составляет 6. Каждая грань куба представляет собой квадрат и имеет одинаковую площадь.

Одно из свойств куба — его диагональ. Диагональ куба — это отрезок, соединяющий противоположные вершины. Длина диагонали куба можно вычислить, умножив длину его стороны на √3.

Кубы встречаются не только в геометрии, но и в различных областях жизни. Они используются, например, в архитектуре, дизайне и 3D-моделировании. Благодаря своим особенностям, кубы часто применяются для создания устойчивых и эстетичных конструкций.

Роль математики в нашей жизни

Одна из важнейших ролей математики заключается в развитии логического мышления и абстрактного мышления. Математические задачи и задания требуют от нас анализировать, рассуждать и находить решения на основе четкой логической цепочки.

Математика также помогает развить навыки решения проблем, критического мышления и построения логических аргументов. Она учит нас оценивать информацию, анализировать данные и принимать обоснованные решения.

Кроме того, математика является основой для различных технологий и научных исследований. Математические модели и методы используются в физике, химии, биологии, компьютерных науках и многих других областях для моделирования, анализа и предсказания различных явлений.

Математика также играет важную роль в экономике и финансах. Ее методы используются для анализа рынка, прогнозирования тенденций и определения оптимальных решений. Без математических моделей и алгоритмов было бы невозможно проводить финансовые расчеты, рассчитывать налоги или прогнозировать стоимость акций.

Таким образом, математика играет незаменимую роль в нашей жизни, обеспечивая нам необходимые инструменты для решения сложных задач, развития мыслительных навыков и понимания окружающего мира.

Comparison Table

Parameters Of Comparison	Square	Cube
Length of edges	The length of edges in a square must always be equal according to its definition.	The length of the edges of cubes can be equal and irregular.
Vertices	A square has only four vertices. Vertices are the points where lines of a shape meet.	The number of vertices given in a cube is eight, which is twice a square.
Dimension	A square is known to be a two-dimensional shape because it doesn’t have depth.	A cube is known to be a three-dimensional shape because it has depth.
Formula of Volume	Square is a 2D shape, and that’s why it doesn’t have the volume to measure.	The formula to figure out the volume of the cube is Side x Side x Side (V= a³).
Formula of Area	The formula to figure out the Area of the square is Area = side x side (length x breadth).	The formula of the total surface area of a cube is 6 x side x side (6a²).

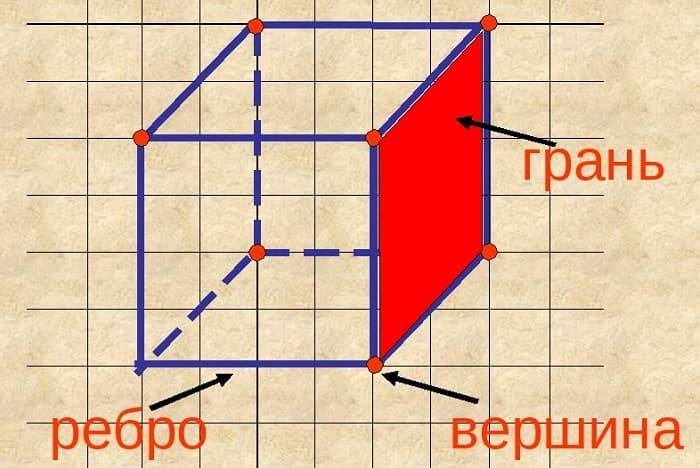
Элементы куба

Основными элементами многогранника являются грани, ребра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями. Другое название страницы.

Интересно, сколько граней у куба и какие у них функции? Всего ребер шесть. Два из них, параллельные друг другу, считаются основаниями, остальные — боковыми.

Грани куба представляют собой пары перпендикуляров, являются квадратами и равны друг другу.

Ребро

Линии, где пересекаются стороны, называются ребрами.

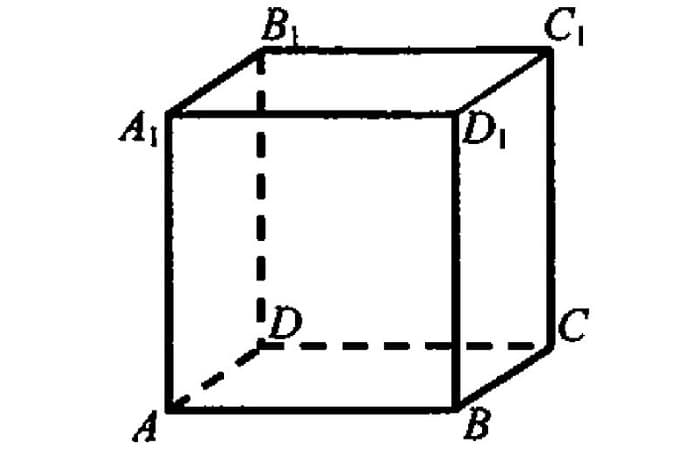
Не все учащиеся могут ответить, сколько ребер у куба. Их двенадцать. Они одинаковой длины. Те из них, которые имеют общий конец, располагают под прямым углом к одному из двух других.

Ребра могут пересекаться в вершине, быть параллельными. Ребра, не лежащие на одной грани, скошены.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.

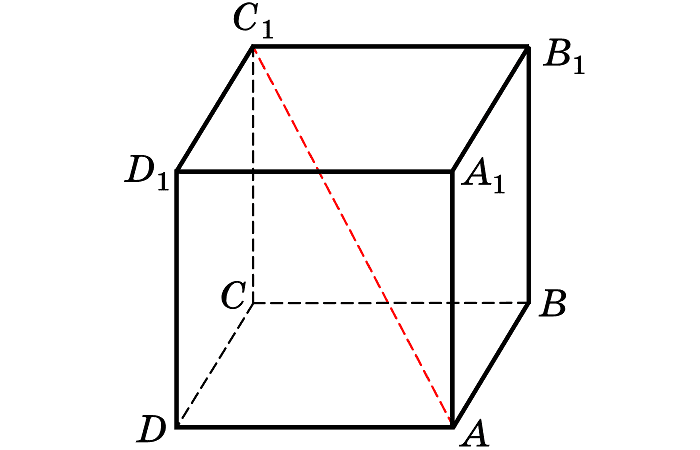
Центром грани считается точка пересечения диагоналей грани — точка, равноудаленная от всех углов и сторон квадрата. Это центр симметрии лица.

Центр куба

Точкой пересечения диагоналей куба является его центр — точка, равноудаленная от всех углов, ребер и сторон многогранника.

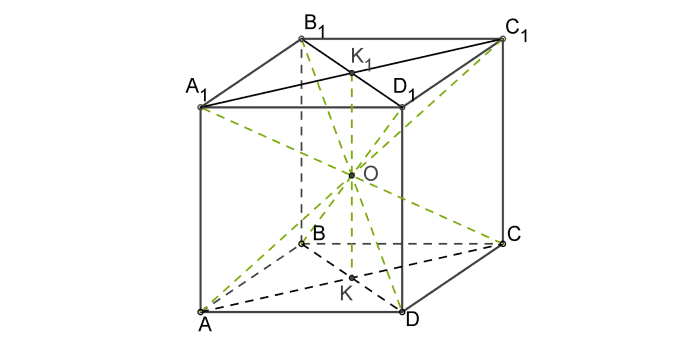
Это центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей с ортогональной (под прямым углом) симметрией. К ним относятся: диагонали куба и прямые линии, проходящие через центр параллельно краям.

Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

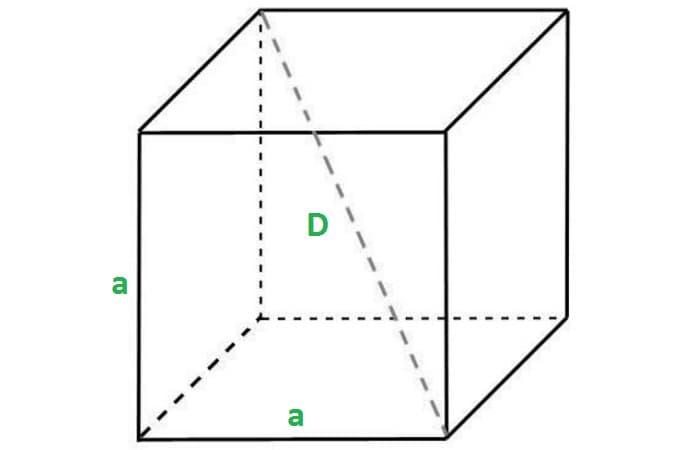
Учитывая, что ребра куба имеют равные размеры a, мы можем найти длину диагонали:

Формула доказывается с помощью дважды примененной теоремы Пифагора.

Диагональ куба является одной из осей симметрии.

Все диагонали в кубе равны между собой, а точка пересечения делится пополам.

Практическое применение куба и квадрата

Куб и квадрат — это геометрические фигуры, которые имеют свое особое применение не только в математике, но и в повседневной жизни.

Что касается квадрата, то его применение можно встретить во многих сферах, например:

Строительство: квадрат используется для определения прямых углов, проверки перпендикулярности и выравнивания поверхностей.
География: квадраты могут использоваться для построения сетки координат на географических картах, что помогает в навигации и определении точных координат.
Графика и дизайн: квадрат может быть использован как основная форма в создании дизайна логотипов, упаковки продуктов и других графических элементов.

Что касается куба, то его применение также можно найти в различных сферах:

Механика: кубы используются для моделирования и расчета механических систем, включая машинные детали и конструкции, например, при проектировании автомобилей или самолетов.
Кристаллография: кубические кристаллы широко применяются в научных исследованиях и промышленности для создания оптических приборов, лазеров и полупроводниковых материалов.
Информационные технологии: кубы используются в алгоритмах и структурах данных, таких как кубы данных, для анализа, обработки и хранения больших объемов информации.

Таким образом, куб и квадрат имеют широкое практическое применение и являются неотъемлемой частью различных областей, включая науку, технологии, строительство и дизайн.

What is Cube?

A cube is a three-dimensional shape built up with six squares putting together face to face. A cube has eight vertices, six faces, and twelve edges. Cube is one of the platonic solids and hexahedrons.

A person is suggested to use the formula to find out the volume of a cube is volume = height x length x width.

If a person only knows the exact measurement of one side of a cube, he can simply figure out the Volume and Area of the cube. The other examples of a cube are rhombohedral, equilateral cuboid, parallelepiped, etc.

A cube consists of Orthogonal projections: faces, edges, vertex figures, and vertices.

A cube is considered to be the most exact shape in a 3-dimensional world. With proper technique, it can be drawn flawlessly.

The shape of the cube is called cubic and has a vital role to play in the equation. A cube is divided into curved surface area and total surface area.

In curved surface area, only four sides of the cube facing each other are included, while in total surface area, all sides of a cube are included. All these faces are in the shape of a square, and their angles are also right angles.

A single vertex of a cube is shared by three faces.

What is Square?

A square is a two-dimensional geometrical shape with four vertices, four edges, and an internal angle of 90 degrees. The square has four right angles inside of it.

It is a regular polygon that shares properties with convex polygon, equilateral polygon, cyclic, isogonal figure, etc. A Square is also defined as a rectangle because its two adjacent sides have a similar length.

The total sum of the square’s angle is 360 degrees. Since it is made of four right angles, other polygons that fit into the definition of a square are rectangle, parallelogram, rhombus, trapezium, etc.

A rectangle is a square because it has two adjacent equal sides. A parallelogram is considered to fit the square’s explanation because it has two adjacent equal sides and a right vertex.

A rhombus can pass for a square because each angle is similar and has a right vertex. A trapezium can be called a square because it has a pair of parallel sides.

When diagonals of some quadrilateral are equal and bisect each other, making a right angle is known as a square.

According to the definition, the parallel sides of a square should be similar. A square has a perimeter and Area.

The circumference is measured with the help of the formula take is p = 4 x side or 4l. And the formula to find out Area is side x side that is written as l².

Сравнение

Уже на первый взгляд понять можно, что отличие куба от квадрата состоит в их трудности. Вторая из данных фигур считается элементарной.

Квадрат всегда принадлежит лишь одной плоскости. Его составляющие – стороны и углы.

Кол-во тех и прочих – 4-ре. Причем в любой группе между элементами встречается равноправие.

Квадрат рассматривается как разновидность прямоугольника, однако в этом случае длина и ширина такие же.

Другой объект – куб – устроен сложнее. Он обладает подобной характеристикой, как объем.

Это тело составлено из 6-ти скреплённых между собой квадратов, которые тут выполняют функцию граней.

Так смотрится геометрический объект в развертке:

Объем дров. Как посчитать кубатуру дров?

https://youtube.com/watch?v=ZZLQIyL7YuU

Параметрами куба считаются не только длина и ширина, но еще высота. И все данные размеры у названного тела равны.

Для нахождения объема необходимо величину любого ребра, объединяющего соседние грани, построить в третью степень.

Если требуется найти поверхностную площадь, то следует размер ребра помножить на себя же и результат сделать больше в шесть раз. Между тем площадь квадрата вычисляется легче – по произведению 2-ух сторон.

Любой из предметов обсуждения обладает некоторыми особенностями.

Их содержание для куба сводится к тому, какие прочие многогранники можно включить в указанный объект и как данные фигуры будут находиться. В свойствах также упоминается о сечениях куба.

В отношении квадрата говорится о равенстве и обоюдной перпендикулярности его диагоналей, а еще о некоторых остальных свойствах.
Иногда родители не знают, как на доступном уровне объяснить ребенку, в чем разница между кубом и квадратом.

В этом случае можно вырезать последний из картона и показать, какой он плоский. Потом необходимо взять выполненный из бумаги или вылепленный из пластилина куб и показать его с каждой стороны, чтобы хорошо просматривался объем.

Пересечение куба плоскостью

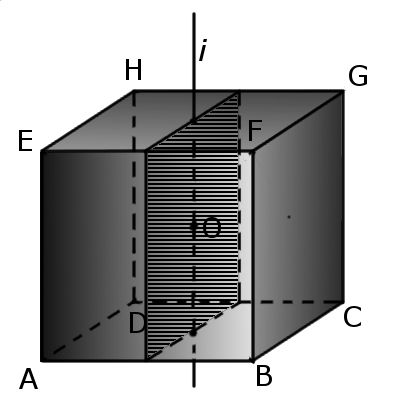
1. Если разрезать куб плоскостью, проходящей через центр куба и центры двух противоположных граней, то сечение будет иметь квадрат, длина стороны будет равна длине ребра куба. Эта плоскость делит куб на два равных прямоугольных параллелепипеда.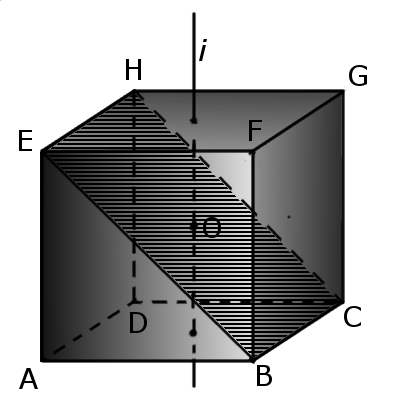
2. Если куб с ребром а пересечь плоскостью, проходящей через центр куба и два параллельных ребра, то сечение будет иметь прямоугольник со сторонами а и а√2, с площадью поперечного сечения а2√2. Эта плоскость делит куб на две равные призмы.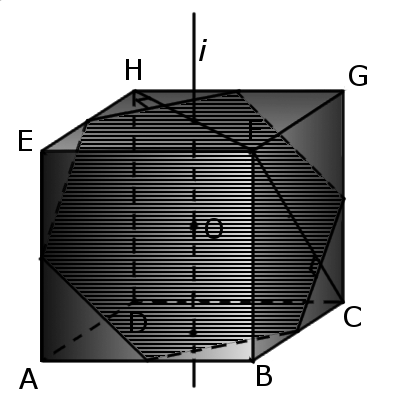
3. Если разрезать куб плоскостью, проходящей через центр и середины шести граней, то сечение будет иметь правильный шестиугольник со стороной a√2/2, площадью поперечного сечения a2(3√3)/4 . В кубе одна из диагоналей (FC) каждой грани перпендикулярна стороне шестиугольника.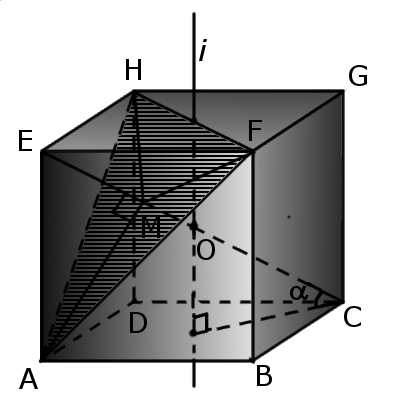
4. Если пересечь куб плоскостью, проходящей через три угла куба, то сечение будет иметь правильный треугольник со стороной а√2, площадью поперечного сечения а2√3/2 и объемом большей части 5а3/. 6 и меньшее — а3/6. Одна из диагоналей куба (ЕС) перпендикулярна плоскости сечения, проходит через центр треугольника (М) и делится плоскостью в отношении МС:ЕМ = 2:1.

Публикация «Конспект интегрированного занятия по ФЭМП „Куб и квадрат“ в старшей группе» размещена в разделах

Геометрические фигуры. Конспекты занятий по математике
Квадрат. Геометрическая фигура
Конспекты занятий. Все конспекты
Математика. Конспекты занятий по ФЭМП
Математика. Математические представления, ФЭМП
Старшая группа
Темочки
Конкурс для воспитателей и педагогов «Лучший конспект занятия (НОД)» февраль 2018

– сформировать опыт самостоятельного преодоления затруднения под руководством педагога на основе рефлексивного метода, опыт самоконтроля;

– совершенствовать умение соотносить цифру с количеством, сравнивать совокупности и устанавливать между ними равенство;

– упражнять в решении логических задач и задач на смекалку;

– формировать у детей интерес к математике, чувство уверенности в своих знаниях.

– тренировать мыслительные операции – анализ, сравнение, обобщение, абстрагирование.

Развивающие:

– развивать внимание, память, речь, фантазию, воображение, логическое мышление, творческие способности, инициативность;

– развивать мелкую моторику рук.

Воспитывающие:

– воспитывать положительную мотивацию к учению, интереса к математике;

– воспитывать доброжелательного отношения друг к другу.

Демонстрационный материал:

Игрушка Старичка – лесовичка, геометрические фигуры, магнитная доска, поднос, красные и желтые цветы из картона, плакат с рисунком цветочной поляны, плакат с рисунком геометрической страны.

Раздаточный материал:

-наборы геометрических плоскостных и объемных фигур, альбомные листы по количеству детей.

Методы и приемы: объяснение, указание, пояснение, вопросы, показ, игровой прием, поощрение, педагогическая оценка.

Образовательные области:

Познавательное развитие (ФЭМП);

Речевое развитие;

Художественно-эстетическое развитие (конструктивно-модельная деятельность);

Социализация (игровая деятельность).

Возведение в степень и степень числа

В математике возведение в степень — это операция, при которой число умножается само на себя определенное количество раз. Результат такой операции называется степенью числа.

Степень числа обозначается с помощью знака «^». Например, 2^3 означает возведение числа 2 в третью степень.

Возведение в степень имеет следующие основные свойства:

Умножение степеней одного и того же числа. Если нужно умножить две степени одного и того же числа, то нужно сложить их показатели степеней. Например: 2^3 * 2^4 = 2^(3+4) = 2^7.
Деление степеней одного и того же числа. Если нужно разделить две степени одного и того же числа, то нужно вычесть из показателя степень делителя показатель степени делителя. Например: 2^5 / 2^2 = 2^(5-2) = 2^3.
Возведение степени в степень. Если нужно возвести степень в еще одну степень, то нужно умножить их показатели степеней. Например: (2^3)^2 = 2^(3*2) = 2^6.

Кроме того, степень числа может быть как положительной, так и отрицательной. У отрицательной степени число переворачивается (делится на 1), а затем возводится в положительную степень. Например: 2^(-3) = 1 / (2^3) = 1 / 8 = 0.125.

Степени чисел широко применяются в различных областях науки и техники, особенно в арифметике, алгебре и геометрии.

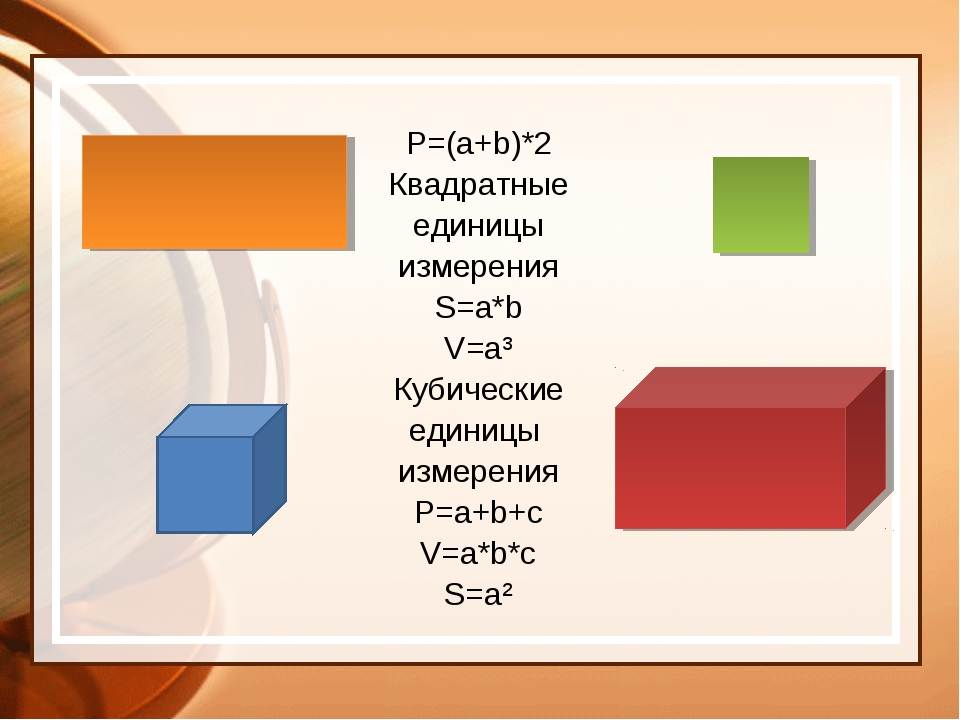
Площадь и объем квадратов и кубов

Площадь квадрата — это площадь, занимаемая поверхностью квадрата. Для нахождения площади квадрата нужно умножить длину его стороны на саму себя. Формула для вычисления площади квадрата выглядит так: S = a^2, где S — площадь, а — длина стороны квадрата.

Площадь куба — это площадь всех его граней в сумме. Для определения площади куба нужно умножить площадь одной грани на 6. Формула для вычисления площади куба: S = 6a^2, где S — площадь, а — длина стороны куба.

Объем куба — это объем пространства, занимаемого кубом. Для определения объема куба нужно умножить длину его стороны на саму себя, а затем умножить полученный результат на саму себя еще раз. Формула для вычисления объема куба: V = a^3, где V — объем, а — длина стороны куба.

Понимание площади и объема квадратов и кубов помогает нам в решении различных математических и геометрических задач

Также это важно для понимания объема и площади других геометрических фигур и трехмерных объектов