Макс Невелов Основные отличия между реальным и идеальным газами
Молекулярная структура:
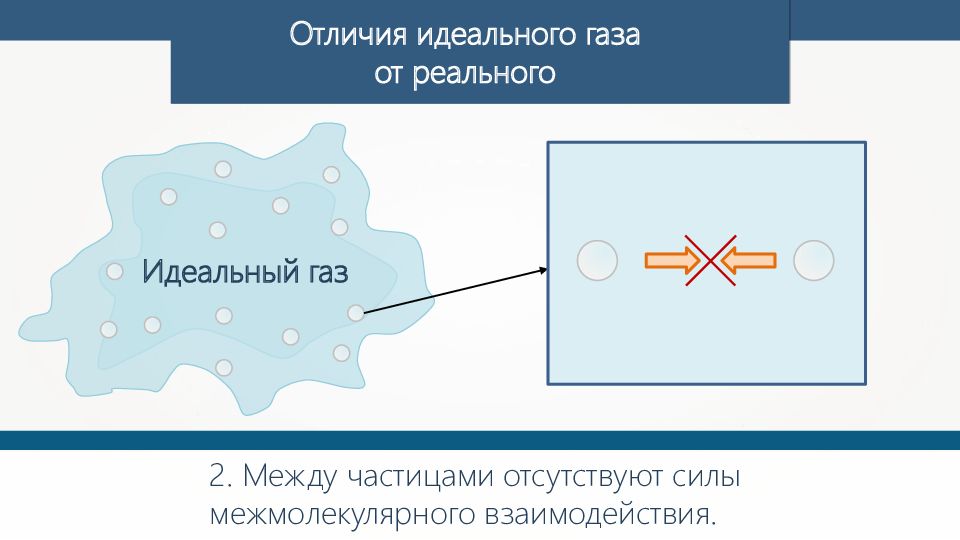
Идеальный газ представляет собой гипотетическую модель, в которой газовые молекулы рассматриваются как точечные частицы без объема и взаимодействия друг с другом. Реальный газ, напротив, имеет конечные размеры и взаимодействует с другими молекулами с помощью сил притяжения и отталкивания.
Уравнение состояния:
Идеальный газ описывается уравнением состояния PV = nRT, где P — давление, V — объем, n — количество вещества, R — универсальная газовая постоянная, а T — температура. Уравнение состояния реального газа сложнее и может включать дополнительные параметры, такие как коэффициент сжимаемости или корректирующие члены, учитывающие взаимодействие молекул.
Адиабатическое поведение:
Идеальный газ при адиабатическом процессе не испытывает потерь или получения тепла. Его температура меняется с плавностью в соответствии с уравнением PV^(γ) = const, где γ — показатель адиабаты. Реальный газ может проявлять диссипативные эффекты, такие как диффузия и тепловое расширение, которые могут привести к изменению его состояния.
На конкретное вещество:
Идеальный газ является универсальной моделью и применим для любого газообразного вещества в определенных условиях. Реальный газ имеет свои специфические свойства, которые зависят от молекулярной структуры вещества.
Важно отметить, что идеальный газ является удобной и простой моделью для изучения основных закономерностей газового поведения, но в реальности газы редко соответствуют этой модели в точности. Основные отличия между реальным и идеальным газом отражают их различия в молекулярной структуре, уравнении состояния, адиабатическом поведении и специфических свойствах каждого вещества
Правила применения для решения задач
С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса и один трех параметров (давление, температура или объем) остаются неизменными.
Количественные зависимости между двумя параметрами газа при фиксированном третьем параметре называют газовыми законами.
В зависимости от того, какой параметр остается неизменным, различают разные процессы:
- изотермический процесс (T=const);
- изохорный процесс (V=const);
- изобарный процесс (p=const).
Изотермический процесс (T=const)
Для поддержания постоянной температуры газа необходимо, чтобы он мог обмениваться теплотой с большой системой — термостатом. Им может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса.
Согласно уравнению Клапейрона-Менделеева, в любом состоянии с неизменной температурой произведение давления газа на объем одно и то же, то есть постоянно:
Этот закон был открыт экспериментально английским ученым Бойлем и несколько позднее французским ученым Мариоттом. Именно поэтому он называется законом Бойля-Мариотта.
Закон Бойля-Мариотта справедлив для любых газов, а также для смеси газов (например, для воздуха).
Зависимость давления газа от объема при постоянной температуре изображается графической кривой — изотермой. Изотерма для различных температур представлена в координатах pV на рис.1. и представляет собой гиперболу.
Рис.1. Изотерма в pV — координатах.
В изотермических условиях проводятся различные физико-химические процессы. Рассмотрим каким образом уравнение состояния идеального газа можно применить в задачах.
Таким образом,
Откуда можем найти начальный объем:
Откуда
Ответ: первоначальный объем газа был равен 8 л.
Изохорный процесс (V=const)
Из уравнения состояния следует, что отношение давлений газа данной массы при постоянном объеме равно отношению его абсолютных температур:
Газовый закон был установлен экспериментально в 1787 г. французским физиком Ж. Шарлем и носит название закона Шарля: давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре.
Так, если в качестве одного из состояний газа выбрать состояние газа при нормальных условиях, тогда
Зависимость давления газа от температуры при постоянном объеме графически изображается прямой, которая называется изохорой (Рис.2).
Рис.2 Изображение изохоры в pT-координатах.
Рассмотрим правила применения изохорного режима для решения задач.
Откуда
Ответ: 600 К.
Изобарный процесс (p=const)
Из уравнения Клапейрона-Менделеева вытекает, что отношение объемов газа данной массы при постоянном давлении равно отношению его абсолютных температур.
Если в качестве второго состояния газа выбрать состояние при нормальных условиях (нормальном атмосферном давлении, температуре таяния льда) следует:
Этот газовый закон был установлен экспериментально в 1802 г французским ученым Гей-Люссаком.
Закон Гей-Люссака: объем данной массы газа при постоянном давлении прямо пропорционален абсолютной температуре.
Зависимость объема газа от температуры при постоянном давлении графически изображается прямой, которая называется изобарой (Рис.3).
Рис. 3. Изобара в VT-координатах.
Перейдем к абсолютной температуре:
Ответ: плотность вырастет в 3 раза.
Откуда,
Ответ: Начальная температура газа была равна 350 К или 77 °C
Влажность воздуха
Поскольку 2/3 земной поверхности занимает вода, то в воздухе всегда содержится водяной пар. За год на Земле испаряется 4,25*1014 т воды. По отношению ко всем газам, содержащимся в атмосфере Земли, водяной пар занимает всего около 1%.
Для описания состояния водяного пара в атмосфере Земли используют уравнение состояния идеального газа.
Физическая величина, характеризующая содержание в воздухе водяного пара, называется влажностью воздуха.
Относительная влажность воздуха определяется как отношение парциального давления p водяного пара, содержащегося в воздухе при данной температуре, к давлению насыщенного пара p при той же температуре:
Относительная влажность воздуха показывает, насколько водяной пар в данных условиях далек от насыщения. Именно от этого зависит интенсивность испарения воды и потери влаги живыми организмами. Для человека наиболее благоприятна относительная влажность, равная 40-60%.
В метеорологии важно знать абсолютную влажность воздуха, т.е. массу водяного пара, содержащегося в единице объема воздуха (плотность водяного пара в воздухе)
На практике измеряется в г/м3.
С уменьшением температуры воздуха водяной пар переходит в насыщенное состояние. Точка росы характеризует температуру, при которой пар становится насыщенным.
Идеальные и реальные газы в термодинамике
Рисунок 2. Законы реальных газов. Автор24 — интернет-биржа студенческих работ
Получи помощь с рефератом от ИИ-шки
ИИ ответит за 2 минуты
Определение 1
Реальные газы – это существующие в природе газы, чьи молекулы обладают конечным объемом, а между ними при этом имеются силы притяжения, оказывающие существенное влияние на их энергетические параметры.
Молекулы реального газа пребывают в непрерывно-хаотичном движении, иными словами – им присуща кинетическая энергия движения. Существование между молекулами гравитационных и электромагнитных силовых взаимосвязей говорит об обладании ими еще и потенциальной энергии взаимодействия, зависящей от расстояния между молекулами.
Замечание 1
С целью упрощения исследования свойств газообразного рабочего тела в термодинамике вводится такое понятие, как «идеальный газ», представляющий собой воображаемый газ, внутри которого молекулы рассматриваются в формате материальных точек, обладающих определенной массой, однако силы взаимодействия между такими точками при этом не учитываются (при детальном анализе состояния рабочего тела и процессов, происходящих в нем).
В случае с большими объемами и незначительным давлением, когда расстояние между молекулами многократно превышает собственные размеры молекул, а также когда наблюдаются достаточно высокие температуры и довольно большая интенсивность хаотического молекулярного движения, происходит процесс их слабого взаимодействия между собой.
В такой ситуации возникают условия, при которых реальный газ может с определенной степенью приближения считаться идеальным, что, в свою очередь, позволяет производить расчеты для реальных газов на базе специальных уравнений и зависимостей, выведенных для идеальных газов, что существенно упрощает расчеты и понимание сути происходящих в газах процессов
Это объясняет важность изучения термодинамических свойств газов не только с теоретической, но и с практической точки зрения
Законы Шарля, Авогадро и Дальтона
Закон Шарля (второй закон Гей-Люссака) говорит об изменении абсолютного давления газа (при условии неизменного удельного объема) прямо пропорционального смене показателя абсолютных температур:
Экспериментальным способом зависимость давления газа от температуры (при постоянном объёме) в 1787 году установил физик Ж.Шарль, занимавшийся исследованием термодинамических процессов, присутствующих в идеальных газах. Несмотря на отсутствие публикации трудов ученого, его идеи активно подхватили такие физики, как Г.Амонтон и другие. Это, в свою очередь, спровоцировало проблему установления авторства некоторых основных законов термодинамики, что представляет предмет спора между экспертами на сегодняшний день.
Открытая и описанная ученым закономерность является справедливой в системах с удельным объемом (неизменным параметром) и температурой, давлением (переменными показателями). Подобные термодинамические процессы (при условии постоянного объема) называются изохорными (изохорическими).
Согласно концепции закона Авогадро, все газы (в условиях одинакового давления и температуры) в равных объемах будут содержать равное число молекул. Иными словами, закон утверждает, что объем киломоля разнообразных газов (при аналогичных физических условиях) становится одинаковым. Данный закон в 1811 году описал итальянский физик А.Авогадро.
Рисунок 4. Закон Авогадро. Автор24 — интернет-биржа студенческих работ
Рабочее тело, которое используется в термодинамических установках, в стандартных случаях представляет собой смесь, сформировавшуюся из нескольких газов. В качестве примера можно привести двигатели внутреннего сгорания, в состав продуктов сгорания которых (имеется в виду рабочее тело) будут входить:
- водород;
- кислород;
- азот;
- окись углерода;
- углекислый газ;
- водяные пары воды;
- некоторые другие газообразные вещества.
В 1801 году английский ученый-физик Д.Дальтон установил закон, исходя из концепции которого, давление, оказываемое смесью, становится равнозначным сумме парциальных давлений у отдельных газов, состоящих в составе смеси.
Парциальным давлением считается давление компонента смеси, которое он мог бы создавать, пребывая в одиночном состоянии в занимаемом смесью объеме при ее определенной температуре. Данное утверждение легко доказывается на основании определенных выводов, сформированных из закона Бойля – Мариотта, при рассмотрении парциальных компонентов газовой смеси по отдельности и в совокупности.
Закон Дальтона считается применимым по своей актуальности для идеальных газов. Также он может применяться и в отношении реальных газов, обладающих близкими к идеальным физическим параметрам свойствами.
Что такое идеальный газ?
Идеальным газом называется газовое состояние вещества, которое следует основным постулатам кинетической теории газов и не имеет взаимодействия между молекулами. Такое состояние возможно лишь при определенных условиях, включая низкое давление и высокую температуру.
Основной характеристикой идеального газа является его уравнение состояния, которое описывает зависимость между давлением, объемом и температурой. В идеальном газе это уравнение выглядит следующим образом:
pV = nRT,
где p — давление, V — объем, n — количество вещества (в молях), R — универсальная газовая постоянная, T — температура в градусах Кельвина.
Основная особенность идеального газа заключается в отсутствии взаимодействия между молекулами, что позволяет просто и легко описать его свойства и поведение. Идеальный газ является абстрактной моделью, которая позволяет упростить изучение газового состояния вещества и применять его в множестве физических задач и расчетов.
Определение идеального газа
Основное предположение о идеальном газе заключается в том, что между его молекулами нет притяжения или отталкивания, и они движутся в случайном направлении со случайной скоростью. Это означает, что объем идеального газа можно занять любым количеством газа, и он будет равен сумме объемов его молекул.
Идеальный газ также характеризуется уравнением состояния, известным как уравнение состояния идеального газа. В этом уравнении учитываются такие параметры, как давление, температура и объем газа, чтобы определить его состояние.
Необходимо отметить, что идеальный газ является упрощенной моделью реальных газов, и в реальности все газы взаимодействуют друг с другом и обладают объемом. Однако, модель идеального газа все еще широко используется при решении многих физических задач, так как она позволяет упростить математические выкладки и облегчить анализ газового поведения.
Основные особенности идеального газа
Вот основные особенности идеального газа:
- Молекулы не взаимодействуют между собой: В идеальном газе молекулы не взаимодействуют между собой, они движутся независимо друг от друга. Это позволяет упростить расчеты идеального газа, поскольку не нужно учитывать сложные взаимодействия между молекулами.
- Объем газа ничтожно мал по сравнению с объемом контейнера: Идеальный газ представляет собой множество молекул, занимающих очень маленький объем по сравнению с объемом сосуда, в котором он содержится. Поэтому объем газа можно считать пренебрежимо малым по сравнению с объемом контейнера.
- Молекулы движутся хаотично и со случайной скоростью: Молекулы идеального газа движутся хаотично и со случайной скоростью. Их движение можно описать с помощью теории статистики.
- Закон Бойля-Мариотта: При постоянной температуре объем идеального газа обратно пропорционален давлению, то есть при увеличении давления объем газа уменьшается, и наоборот.
- Закон Чарлза: При постоянном давлении объем идеального газа прямо пропорционален температуре, то есть при увеличении температуры объем газа также увеличивается.
- Закон Гей-Люссака: При постоянном объеме идеальный газ давление прямо пропорционально температуре, то есть при увеличении температуры давление газа также увеличивается.
- Уравнение состояния идеального газа: Для описания состояния идеального газа используется уравнение состояния, которое позволяет рассчитать его объем, давление и температуру.
Идеальный газ является удобной моделью для изучения свойств газов и применяется во многих областях, таких как физика, химия и инженерия.
Формула состояния идеального газа
Формула состояния идеального газа записывается следующим образом:
PV = nRT
где:
- P — давление газа в паскалях (Па)
- V — объем газа в кубических метрах (м³)
- n — количество вещества газа в молях (моль)
- R — универсальная газовая постоянная, примерное значение которой составляет 8,314 Дж/(моль·К)
- T — абсолютная температура газа в кельвинах (К)
Формула состояния идеального газа позволяет рассчитывать различные характеристики газа, такие как давление, объем и температура, при различных условиях. Она основана на следующих предположениях: частицы газа считаются масселооскми точками, между ними нет взаимодействий, и они совершают абсолютно безупречные упругие столкновения.
Формула состояния идеального газа является приближенной для реальных газов, так как реальные газы обладают такими свойствами, как силы взаимодействия между частицами и объем самой частицы. Однако, формула состояния идеального газа успешно описывает многое из того, что происходит с газами в широком диапазоне условий.
Измерение влажности воздуха
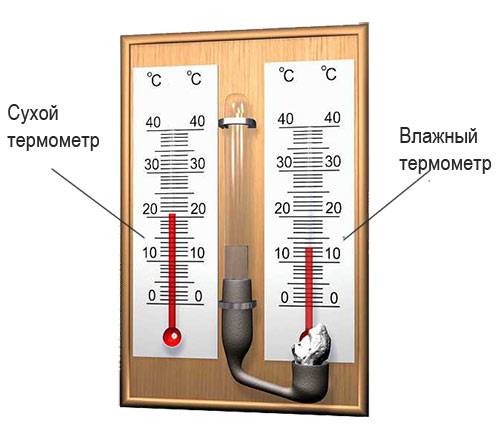
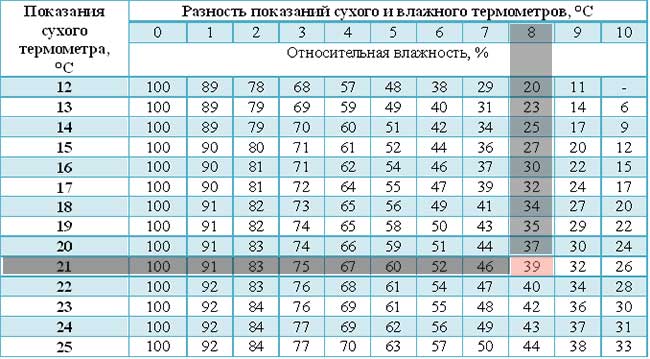
С помощью психрометра фиксируют разницу температур двух термометров – сухого и влажного. По этой разнице и температуре сухого термометра устанавливают влажность воздуха по психрометрической таблице:
Действие волосного гигрометра основано на способности обезжиренного человеческого волоса изменять свою длину в зависимости от влажности воздуха.
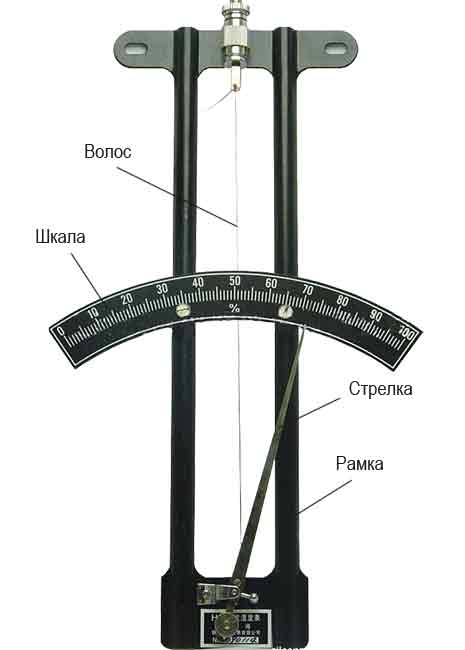
Волос соединяется со стрелкой прибора, шкала которого градуируется в процентах относительной влажности.
С помощью конденсационного гигрометра измеряют точку росы – температуру, до которой необходимо охладить воздух, чтобы содержащийся в нем водяной пар, остывая, стал насыщенным.
Начиная с этой температуры, охлаждение воздуха сопровождается появлением капелек росы на зеркальном сосуде, температуру которого понижают, прокачивая грушей воздух через легкокипящую жидкость.
В настоящее время нашли широкое применение как стрелочные, так и электронные цифровые гигрометры с жидкокристаллическим экраном.
Определенную влажность воздуха нужно поддерживать в библиотеках, музеях для лучшего сохранения книг, картин и других экспонатов. Для уменьшения электризации нитей в ткацких цехах создают высокую влажность. Строгий контроль влажности ведется в кондитерских цехах.
Вопросы для самоконтроля по блоку «Реальные газы»
- Что называют испарением? Конденсацией?
- Укажите причины, от которых зависит скорость испарения жидкости?
- Как изменяется внутренняя энергия жидкости при ее испарении?
- Чем отличается кипение жидкости от ее испарения?
- Опишите процессы, протекающие в закрытом с жидкостью сосуде. Что такое динамическое равновесие?
- Какой пар называют насыщенным?
- Почему давление насыщенного пара не зависит от объема, в котором он находится?
- Нарисуйте и объясните изотерму реального газа.
- Изобразите графически и объясните зависимость давления насыщенного пара от температуры при постоянном давлении.
- Что понимают под влажностью воздуха?
- Что такое абсолютная влажность воздуха? В каких единицах ее выражают?
- Что называют относительной влажностью воздуха?
- Что такое точка росы?
- С помощью каких приборов определяют влажность воздуха?
Идеальный газ — что это за состояние
Идеальными считают разреженные газы. Особенно близкими к идеальным считают гелий и водород.
Когда используют модель идеального газа, то предполагается:
- Составляющие газ частицы не взаимодействуют друг с другом, то есть их размеры пренебрежимо малы, поэтому в объеме, занятом идеальным газом, нет взаимных столкновений частиц. Частицы идеального газа претерпевают столкновения только со стенками сосудов.
- Молекулы газа движутся хаотически, а соударения между молекулами и их удары о стенки сосуда упругие, то есть не приводят к потере энергии в системе.
Таким образом, между частицами газа нет дальнодействующего взаимодействия, например, электростатического и гравитационного. Дополнительное условия упругих столкновений между молекулами и стенками сосуда в рамках молекулярно-кинетической теории приводит к термодинамике идеального газа.
| № | Допущения для описания модели идеального газа |
| 1 | Размеры молекул пренебрежимо малы по сравнению со средним расстоянием между ними, так что суммарный объем, занимаемый молекулами, много меньше объема сосуда. |
| 2 | Импульс передается только при соударениях, то есть силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях молекул друг с другом. |
| 3 | Соударение частиц между собой и со стенками сосуда абсолютно упругие. |
| 4 | Количество молекул в газе велико и фиксировано, что позволяет вычислять средние величины по малому (по сравнению с размерами системы) объему. |
| 5 | Газ находится в термодинамическом равновесии со стенками сосуда и дополнительно отсутствуют макроскопические потоки вещества. Тут следует уточнить, что градиенты термодинамических величин могут иметь место, как например, при включении внешнего поля, к примеру, гравитационного. |
Таблица 1. Допущения, которые лежат в основе молекулярно-кинетической теории описания физической модели идеального газа.
идеальный и реальный газ
(Подробно)
В
обычных условиях, когда средняя
потенциальная энергия взаимодействия
молекул много меньше их средней
кинетической энергии, свойства реальных
газов незначительно отличаются от
свойств идеального газа и к реальным
газам применимы законы, установленные
для идеального газа. Другими словами
понятие( Реальный газ) ввели физики, для
того, чтобы был так называемый эталон
газа. И в нём были приняты следующие
допущения:
1)Размеры
молекул малы по сравнению со средним
расстоянием между ними; молекулы можно
принимать за материальные точки.
2)Силы
притяжения между молекулыми не
учитываются, а ситы отталкивания
возникают только при соударениях
молекул.
3)Молекулы
сталкиваются друг с другом как абсолютно
упругие шары, движение которых описывается
законами механики.
Чтобы
создать идеальный газ, нужно пренебречь
межмолекулярным взаимодействием, но
для реализации данного условия необходимо
увеличивать температуру газа и расстояние
между молкулами, тоесть разряжать газ.
Например, водород, кислород, азот при
н.у.(нормальных условиях) в атмосере
можно рассматривать
как идеальные газы
Слово
«идеальный» означает «воображаемый,
реально не существующий».
Реальный
газ отличется
от идеального наличием взаимодействия
молекул. При малых плоностях в нем
преобладают силы притяжения, что приводит
к появлению дополнительного давления:
газ как бы сжимает сам себя. При больших
плотностях действуют силы отталкивания,
вследтсвие чего молекула не допускает
проникновения других молекул в занимаемый
ею объем. Пренебрегать собственным
объемом молекул реального газа нельзя.
При
не слишком высоком давлении (например,
при атмосферном) и не слишком низкой
температуре (например, при комнатной)
реальный газ с достаточной степенью
точности подчиняется законам идеального
газа.
Для
объяснения свойств вещества в газообразном
состоянии используется модель идеального
газа. Идеальным принято
считать газ, если:
а)
между молекулами отсутствуют силы
притяжения, т. е. молекулы ведут себя
как абсолютно упругие тела;
б)
газ очень, разрежен, т. е. расстояние
между молекулами намного больше размеров
самих молекул;
в)
тепловое равновесие по всему объему
достигается мгновенно.
Условия,
необходимые для того, чтобы
реальный газ обрел свойства идеального,
осуществляются при соответстсвующем
разрежении реального газа. Некоторые
газы даже при комнатной температуре и
атмосферном давлении слабо отличаются
от идеальных. Основными параметрами
идеального газа являются давление,
объем и температура.
Реальное состояние вещества
Степень отклонения свойств веществ, находящихся в реальном состоянии, от свойств идеального газа зависит от температуры и давления системы, а также от природы вещества. При высоких давлениях плотность паровой фазы может значительно превышать плотность жидкой фазы. Так, при 1500 МПа и 338 К плотность газообразного водорода составляет 130 кг/м3, тогда как плотность жидкого водорода равна 70 кг/м3, а твердого – 80 кг/м3. При плотности 1500 кг/м3 и температуре, превышающей критическую, фактический молярный объем азота в 16 раз больше молярного объема, рассчитанного по уравнению для идеальных газов.
Реальные газы отличаются от идеальных также характером изменения их теплофизических свойств. Теплоемкость идеального газа не зависит от давления, но на реальные газы это правило не распространяется. Вблизи критической точки многие свойства реальных газов изменяются аномально.
Силы, действующие между молекулами, а следовательно, и характер P-V-T функции, определяются тем, какими атомами представлена молекула, их взаимным расположением, а также размерами и формой самой молекулы. На молекулы действуют одновременно силы притяжения и отталкивания. Действие сил притяжения проявляется сильнее с увеличением расстояния между ними, отталкивания – с его уменьшением. Силы притяжения ведут к проявлению давления большей величины, чем давление, создаваемое кинетической энергией молекул, в то время как силы отталкивания уменьшают эффективный объем, доступный для молекулярного движения.
По электрическим свойствам молекулы можно подразделить:
на электронейтральные, симметричные и, как правило, неполярные;
асимметричные и, следовательно, обладающие дипольными, квадрупольными и пр. моментами, а значит, являющиеся полярными;
обладающие остаточным зарядом, который может вызвать молекулярную ассоциацию и образование водородных связей.
Силы межмолекулярного взаимодействия проявляются между всеми молекулами, но наиболее сильными они оказываются при участии полярных молекул и, тем более, в случае молекул, склонных к ассоциации.
В настоящее время разработаны достаточно надежные подходы к прогнозированию свойств неполярных веществ. Для полярных веществ, особенно склонных к ассоциации, предложены приемы прогнозирования, обладающие меньшей универсальностью. Многие из них рассмотрены в данном пособии.
Изотермы реального газа в системе координат P-V существенно отличаются от гиперболы, особенно в области критической точки.
Законы Бойля-Мариотта и Гей-Люссака
В качестве основных законов для идеальных газов в термодинамике задействованы законы:
- Бойля-Мариотта и Гей-Люссака, устанавливающие непосредственные взаимосвязи главных параметров газов, таких как объем, давление, молекулярная масса и температура;
- учения Шарля, Авогадро и Дальтона.
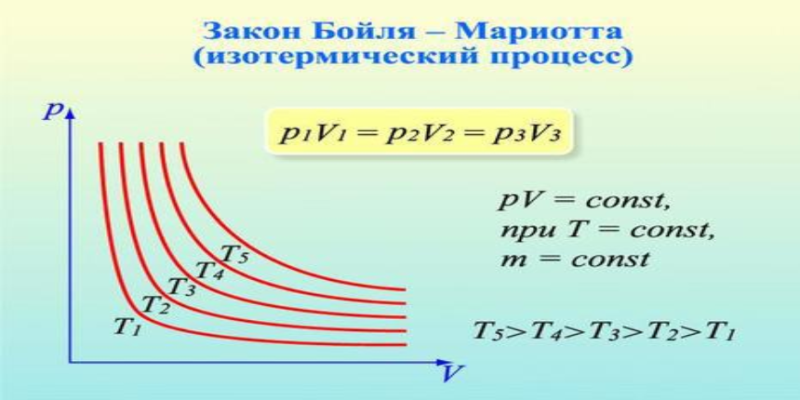Рисунок 3. Закон Бойля – Мариотта. Автор24 — интернет-биржа студенческих работ
Закон Бойля-Мариотта констатирует постоянство величины при неизменности температуры (произведение абсолютного давления газа в изотермическом процессе на его удельный объем). Закон считается справедливым в отношении термодинамических систем с идеальным рабочим телом, в которых температура выступает неизменным параметром, а переменными считаются объем и давление.
Определение 2
Такие процессы называются изотермическими. При них не исключается подвод (или отвод) тепла к термодинамической системе, но тепловая энергия в данном случае не должна воздействовать на температуру газа (рабочего тела), а применяться, например, при выполнении работы методом преобразования в иной вид энергии. В то же время, процессы, исключающие подвод и отвод тепла к термодинамической системе полностью, называют адиабатными.
Применение закона Бойля – Мариотта, способствующего взаимосвязи начальных и конечных величин давления и объёма газа, не ограничивается только изотермическими процессами. Так, он может быть справедливым с высокой степенью точности и в случаях изменения температуры при термодинамическом процессе, но при этом начальная и конечная температуры газа в итоге становятся равнозначными.
Закон Гей-Люссака констатирует изменение удельного объема газообразного вещества при постоянном давлении (процесс называется изобарным) прямо пропорционально изменениям абсолютных температур.
Описанная Гей-Люссаком закономерность является справедливой в системах с одним неизменным параметром (давлением) и переменными параметрами (удельный объем, температура). Подобные термодинамические процессы (протекающие при постоянном давлении), физики называют изобарными (изобарическими).
P-V-T СООТНОШЕНИЯ
Механическое состояние вещества в отличие от термодинамического можно описать при наличии известных величин давления, температуры и объема. Эти три параметра связаны между собой уравнением состояния , поэтому только два из них являются независимыми. Уравнение состояния соответствующего вида может применяться для оценки многих важных свойств чистых веществ и их смесей. Например, для прогнозирования плотности жидкой и паровой фаз, давления пара, критических свойств смесей, равновесия “жидкость-пар”, отклонений энтальпии и энтропии от идеального состояния.
В настоящее время не существует такого уравнения состояния, которое было бы применимо для оценки этих свойств любого органического вещества. На данный момент известно более 150 эмпирических уравнений состояния. Они получены на основе обработки экспериментальных P-V-T-данных, сведений по эффекту Джоуля-Томпсона или данных о теплоемкости реальных газов при различных температурах и давлениях. По степени сложности вся совокупность уравнений состояний может быть разделена на некоторые группы. В данном пособии рассматриваются в сопоставлении уравнения состояния каждой группы, широко применяемые при массовых расчетах. Приводятся также сведения, представляющие исторический интерес.
Начало исследований, посвященных изучению количественных соотношений между давлением, объемом и температурой, положено экспериментами Бойля (1662 г.), в результате которых он пришел к выводу, что при данной температуре объем газа обратно пропорционален его давлению.
Количественное выражение температурного воздействия было установлено Шарлем и Гей-Люссаком (1802 г.), которые обнаружили линейный характер этого отношения.
В 1801 г. Дальтон сформулировал закон парциальных давлений, согласно которому в смеси каждый газ ведет себя так, как если бы он один занимал весь объем. При этом общее давление смеси равно сумме парциальных давлений компонентов.
Парциальным давлением компонента называется то давление, которое оказывал бы газ, входящий в смесь, если бы из нее были удалены остальные газы при условии сохранения первоначальных объема и температуры.
В 1822 г. Каньяр де ля Тур открыл критическое состояние вещества.
В 1834 г. Клапейрон объединил законы Шарля и Бойля и впервые сформулировал закон идеальных газов.
Еще на первоначальном этапе исследований было обнаружено, что закон идеальных газов зачастую дает лишь приблизительное описание реального газа. Эти отклонения объяснялись тем, что молекулы имеют конечный объем и между ними существуют силы межмолекулярного взаимодействия.
В 1873 г. Ван-дер-Ваальс предложил уравнение, в котором количественно учтены оба этих фактора, определены условия сосуществования жидкой и паровой фаз и критическое состояние системы. Уравнение Ван-дер-Ваальса положено в основу многих современных уравнений состояния.
1880 г. – Амага сформулировал закон, который гласит, что объем смеси компонентов представляет собой сумму объемов этих компонентов, каждый из которых находится при температуре и давлении смеси.
1901 г. – Льюис ввел понятие фугитивности.
1927 г. – Урселл вывел, используя методы статистической механики, вириальное уравнение состояния.
В 50-х гг. XX столетия началось активное внедрение принципа соответственных состояний в практику прогнозирования многих свойств органических соединений. Развитие теории по вопросам описания свойств газов и жидкостей продолжается.
Реальный газ, основные понятия и формулы
Что такое реальный газ
Уравнение Менделеева-Клапейрона описывает параметры состояния разреженных газов (находящихся при не слишком больших давлениях и при достаточно высоких температурах). При обычных условиях (т.е. при комнатной температуре и атмосферном давлении) это уравнение применимо ко многим газам (например, таким как азот и кислород). Наиболее близки по своим свойствам к идеальному газу гелий и водород. При низких температурах и высоких давлениях поведение газа начинает существенно отличаться от поведения идеального газа. С повышением плотности газа процессы столкновений играют все большую роль, поэтому размерами молекул и их взаимодействием пренебрегать уже нельзя.
Взаимодействие между молекулами реального газа носит сложный характер, поэтому получить уравнение состояния, которое бы количественно правильно описывало поведение реального газа во всей области возможных изменений его температуры и плотности, не представляется возможным. Можно, однако, записать приближенное уравнение, которое учитывает основные качественные особенности взаимодействия молекул.
Уравнение Ван-дер-Ваальса
Поправка учитывает быстро возрастающие на малых расстояниях силы отталкивания: молекулы как бы занимают определенный объем, меньше которого газ не может быть сжат. Таким образом, поправка к объему характеризует ту часть объема, которая недоступна для движения молекул и равна нескольким суммарным объемам всех молекул, содержащихся в газе.
Поправку
называют внутренним молекулярным давлением. Эта поправка учитывает притяжение молекул, следствием которого является уменьшение давления газа. Молекулы идеального газа, сталкиваясь со стенками сосуда, оказывают на него давление. При учете притяжения на каждую подлетевшую к стенке молекулу действует сила, «отталкивающая» ее от стенки обратно в объем – сила притяжения молекул объема. Это притяжение молекул со стороны объема ослабляет силу удара молекул о стенку, при этом давление на стенку уменьшается на величину .
Значенияпостоянных Ван-дер-Ваальса a и b зависят от природы газа, но не зависят от температуры, Константа (параметр) a характеризует взаимодействие между молекулами на больших расстояниях – дальнодействие сил, параметр b характеризует взаимодействии на малых расстояниях – близкодействие сил взаимодействия.
