Чем отличается действительное изображение от мнимого

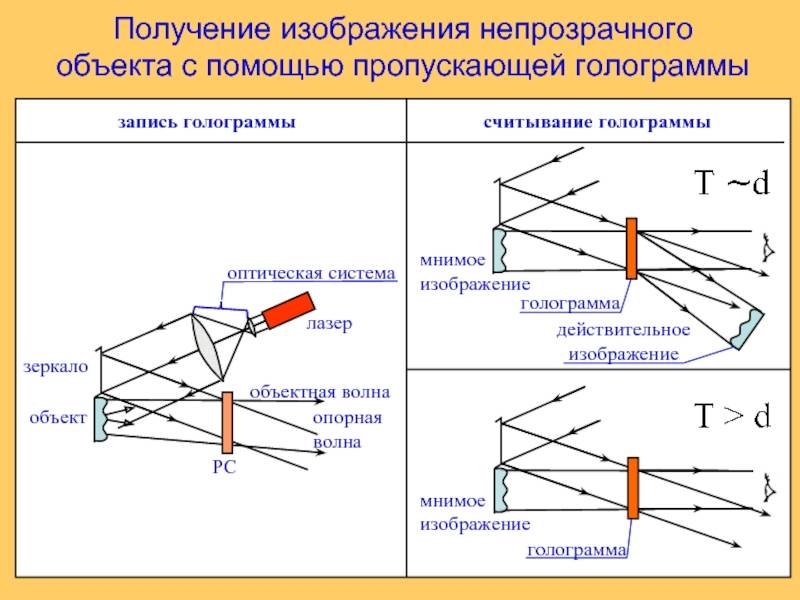
Зеркало. Как видит человек в зеркале?

Полезнейшая вещь есть в любом доме, и используется ежедневно – зеркало. Предметы находятся перед ним, и кажется, что и внутри зеркала есть точно такие же предметы. То, что видимо в зеркале называется изображением предмета.

Свеча перед зеркалом.

Почему человек видит то, чего за зеркальной плоскостью нет? Как это выходит?

Человеческий глаз воспринимает физические тела и вещества с помощью лучей, расходящихся от них во все стороны. Часть этих лучей направлена в глаз, и человек воспринимает окружающие предметы. А теперь, как человек видит что-то в зеркале?

От предмета не все лучи идут к глазу. Некоторая часть их идет на рядом стоящее зеркало. По закону оптики каждый из лучей отражается от зеркальной поверхности под таким же углом, под каким падает.

Пусть точка C стоит перед зеркалом MN. Лучи ведут себя одинаково, поэтому достаточно рассмотреть три из них, чтобы стал понятен их ход.

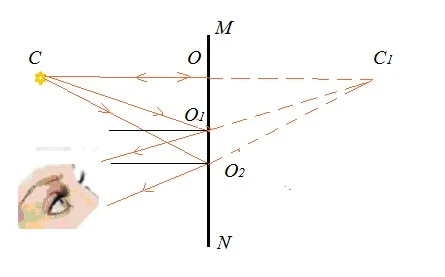Точка С в зеркале MN.

Луч СО падает под углом 0о и отражается тоже под таким же углом (проявляется обратимость лучей света).

Лучи СО₁ и СО₂, отражаясь от зеркала, направляются к глазу, и вместе с ними пучок остальных лучей, которые просто не указаны на чертеже (они ведут себя так же).

Продолжения лучей (сделаны пунктиром) с обратной стороны зеркала пересекутся в точке С_1.Это изображение точки С.

В действительности лучей там нет и точки С₁ тоже нет. Такое изображение называется мнимым изображением.

Используя обычную линейку и свечу можно определить свойства мнимого зеркального изображения.

Для этого надо взять стекло, которое одновременно с отражением дает возможность увидеть за ним линейку.

Стекло вертикально ставится на линейку. Перед стеклом на расстоянии 2 см ставится свечка.

Свечка перед стеклом.

Мнимое изображение свечи находится через 2 см от стекла с обратной стороны. Причем, его высота совпадает с высотой рассматриваемой свечи.

Итак, плоское зеркало дает следующие свойства изображению:

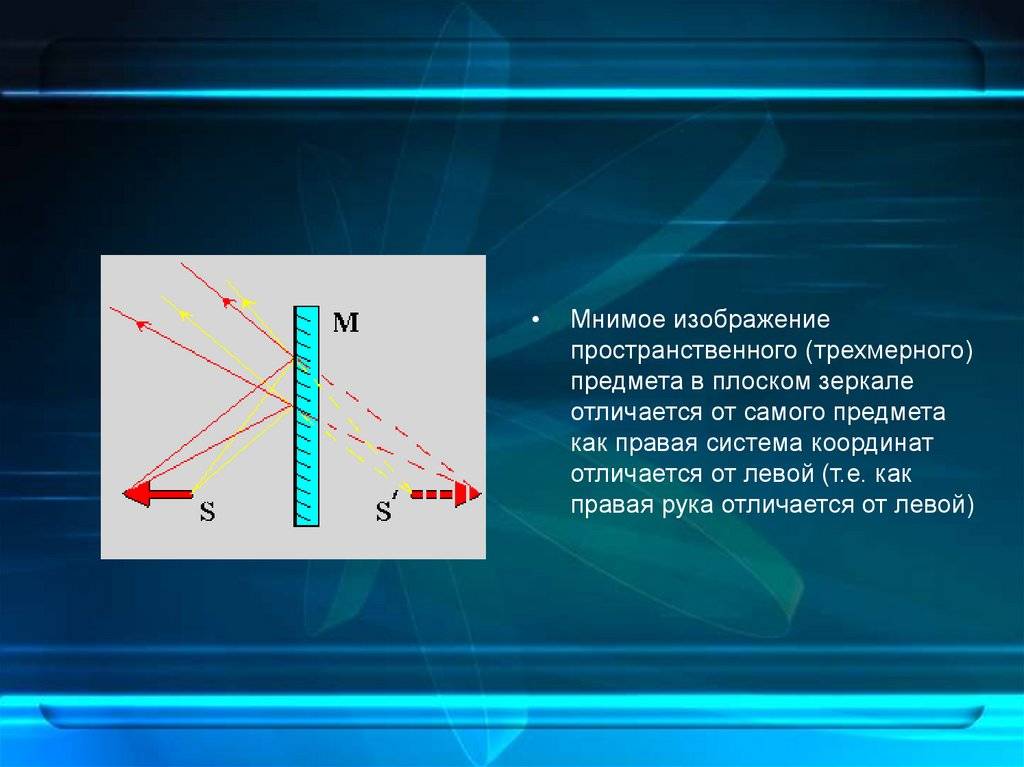
Еще одна особенность зеркальных поверхностей в том, что они дают симметричное изображение. Это видно из простого примера. Если поднести к зеркалу правую руку, там будет видна будто бы левая рука.

Рука в зеркале.

Используя понятие симметрии, можно выполнять чертежи предметов, и их зеркальных изображений.

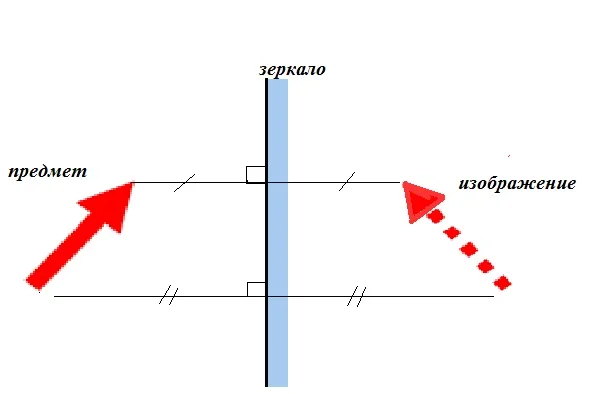Симметрия в зеркальном отражении.

Статьи по этой теме

Оптические линзы и их свойства

Оптические линзы – это прозрачные элементы, используемые для изменения направления и фокусировки света. Они являются неотъемлемой частью многих оптических приборов, таких как очки, микроскопы,…

Фокусное расстояние и его влияние на изображение

Фокусное расстояние – это один из основных параметров объектива, который влияет на качество и характер получаемого изображения. Понимание этого показателя поможет вам выбрать подходящий для…

Как определить положение изображения при помощи линзы

Линзы – это устройства, которые используются для изменения направления и фокусировки света. Они широко применяются в оптике, медицине, фотографии и других областях. Одним из важных свойств линз…

Применение оптических линз в различных устройствах

Что такое оптические линзы?Оптическая линза – это прозрачный предмет, имеющий форму выпуклой или вогнутой поверхности. Она используется для изменения направления и фокусировки…

Оптические аберрации и их влияние на качество изображения

В мире современной оптики, где качество изображения играет важную роль во многих областях, таких как фотография, медицина и наука, понимание оптических аберраций является необходимым….

Как выбрать подходящую линзу для конкретной задачи

При выборе линзы для своих очков каждый человек сталкивается с большим количеством вариантов и разнообразными характеристиками. Часто бывает сложно понять, какая из них будет наиболее…

Особенности работы двойной линзы и ее применение

Двойная линза – это оптическое устройство, состоящее из двух сферических или асферических поверхностей, разделенных воздушным пространством. Она используется для фокусировки света и создания…

Влияние толщины и формы линзы на ее оптические свойства

Оптика является одной из важнейших областей физики, которая изучает свойства и поведение света. Одним из ключевых элементов оптических систем являются линзы, которые используются для…

История развития оптики и применение линз в различных эпохах

Оптика – это наука, изучающая свет и его взаимодействие с материей. Ее история насчитывает тысячелетия и тесно связана с развитием человеческого общества. С самых древних времен люди наблюдали…

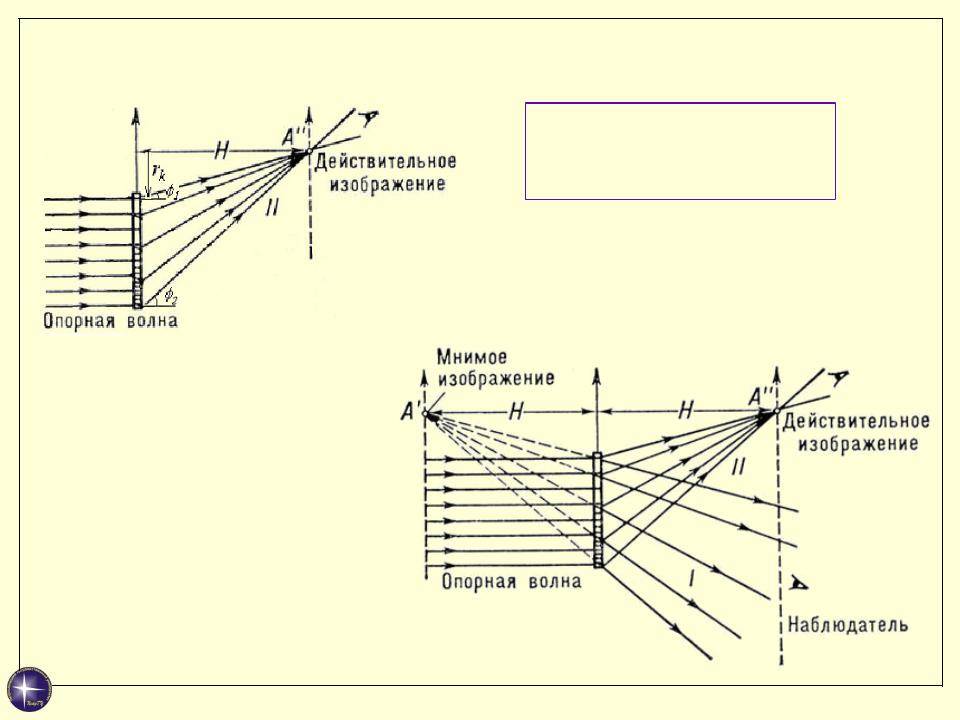
4.6.6 Рассеивающая линза: мнимое изображение точки

К счастью, здесь нет такого разнообразия ситуаций, как для собирающей линзы. Характер изображения не зависит от того, на каком расстоянии предмет находится от рассеивающей линзы, так что случай тут будет один-единственный.

Снова берём луч SO и произвольный луч SX (рис. 4.50
). На выходе из линзы имеем два расходящихся луча OE и XY , которые наш глаз достраивает до пересечения в точке S0
.






	F A0

Рис. 4.50. Мнимое изображение точки S в рассеивающей линзе

Нам снова предстоит доказать теорему об изображении о том, что точка S0
будет одной и той же для всех лучей SX. Действуем с помощью всё тех же трёх пар подобных треугольников:

SAO S0
A0
O; SXS0

OP S0
;

SS0
+ S0
O

b A0
O S0
O

Величина b не зависит от луча SX, поэтому продолжения всех преломлённых лучей XY пересекутся в точке S0
мнимом изображении точки S. Теорема об изображении тем самым полностью доказана.

Вспомним, что для собирающей линзы мы получили аналогичные формулы (4.11
) и (4.15
). В случае a = f их знаменатель обращался в нуль (изображение уходило на бесконечность), и поэтому данный случай разграничивал принципиально разные ситуации a > f и a

А вот у формулы (4.18
) знаменатель не обращается в нуль ни при каком a. Стало быть, для рассеивающей линзы не существует качественно разных ситуаций расположения источника случай тут, как мы и сказали выше, имеется только один.

Если точка S не лежит на главной оптической оси, то для построения её изображения удобны два луча: один идёт через оптический центр, другой параллельно главной оптической оси (рис. 4.51
).

Рис. 4.52. Построение изображения точки S, лежащей на главной оптической оси

Соотношение (4.18
) даёт нам ещё один вариант формулы линзы. Сначала перепишем:

а потом разделим обе части полученного равенства на a:

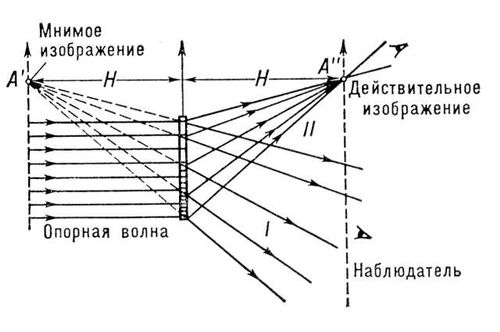
Наше зрение распознает предметы благодаря тому, что они испускают свет (часто он является отраженным). Но лучи от объекта могут встретить на своем пути препятствие в виде какой-либо оптической системы. В результате изображение получается действительным или мнимым. Что подразумевается под этими названиями, как в каждом случае происходит перемещение лучей, и чем отличается действительное изображение от мнимого? Об этом рассказывается ниже.

Глаз. Зрение. Очки

Когда человек надевает очки, оказывается, он создает систему линз, помогающую ему хорошо видеть. Глаз человека или животного – это не просто орган зрения, а оптическая система, созданная природой. Среди частей глаза есть роговица (передняя часть оболочки глаза), прозрачное тело в виде двояко-выпуклой линзы – хрусталик. За хрусталиком располагается стекловидное тело. Эти три составляющие элемента образуют оптическую систему глаза.

Сетчатка, расположенная за стекловидным веществом, является экраном для этой системы.

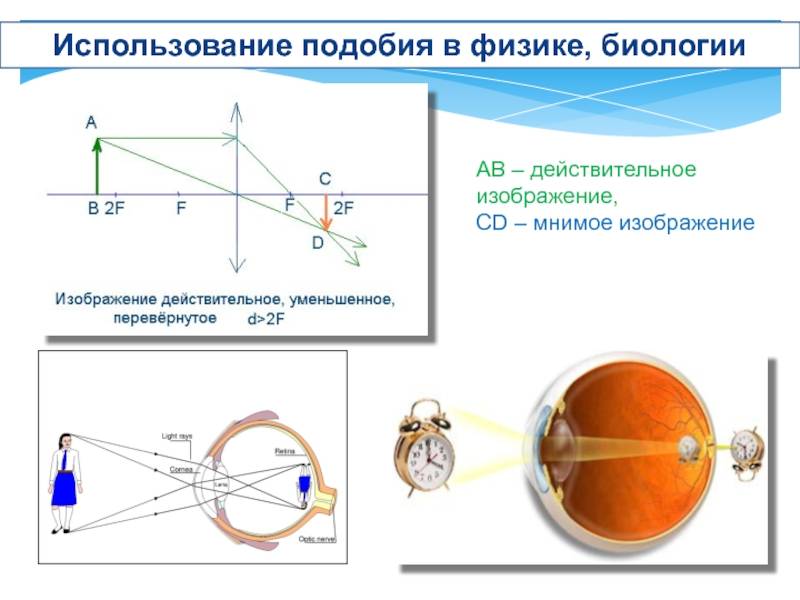
Пройдя через такую систему, световые лучи преобразуются в действительное уменьшенное перевернутое изображение.

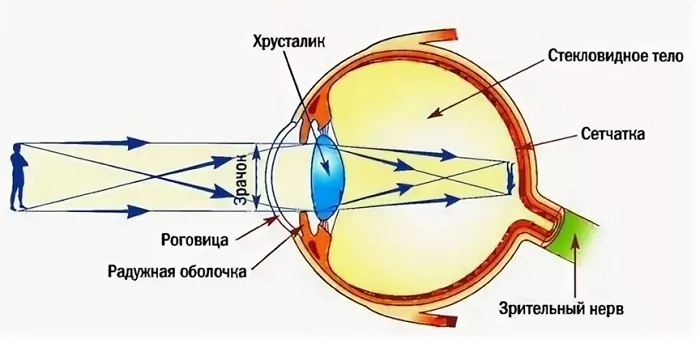Строение глаза.

Человек же получает информацию и другими органами чувств, не только глазами. В результате анализа и корректировки мозгом полученных сведений видит изображение прямым.

Здоровый глаз дает разборчивое изображение прямо на сетчатке. По правилам построения изображений можно сказать, что их характеристики должны быть различными в зависимости от того, где находится рассматриваемый предмет. Так, как же глаз видит при переводе взгляда с близкого предмета на удаленный или наоборот?

В результате эволюционного развития человека глаз приобрел очень полезное свойство приспосабливаться к видению на различных расстояниях. Это свойство называется аккомодацией. При взгляде на удаленные предметы кривизна хрусталика невелика, мышцы глаза его не сдавливают. При этом оптическая сила «живой» линзы слабая.

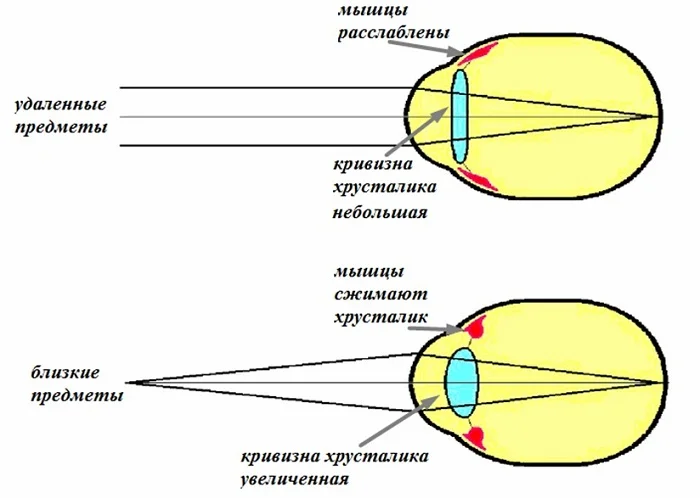Механизм аккомодации.

Взгляд переводится на близкий предмет, мышцы напрягаются, кривизна хрусталика увеличивается, и оптическая сила глаза становится больше.

Так здоровым глазом контролируется видение в различных точках окружающего пространства.

Использовать очки приходится человеку, у которого есть нарушения в оптической системе глаза. Например, это может быть дальнозоркость или близорукость.

С помощью очков глаз получает дополнительные линзы, которые вместе с глазом дают четкое изображение на сетчатке.

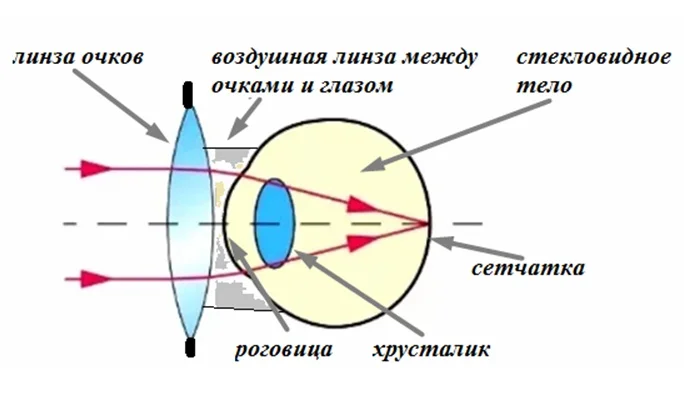Система глаз + очки.

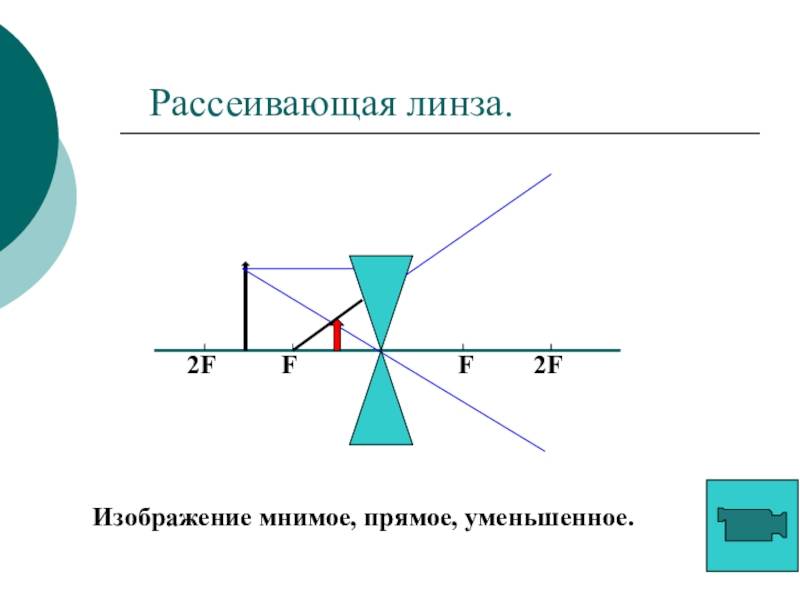
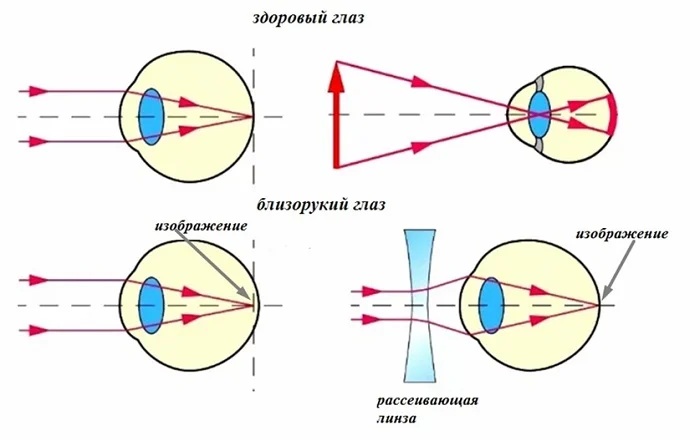
Близорукий глаз дает изображение внутри стекловидного тела перед сетчаткой. Для исправления этого дефекта нужно ослабить оптическую силу глаза, применив рассеивающую линзу.

Наоборот, дальнозоркому глазу нужно увеличение оптической силы, что и делает собирающая линза. Даваемое за сетчаткой изображение переносится на сетчатку.

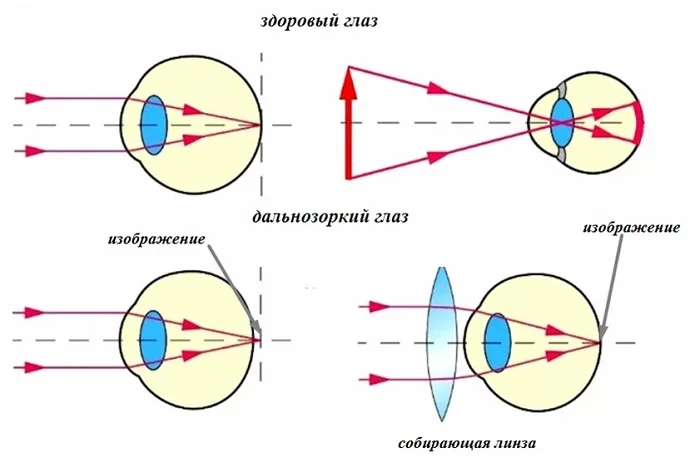
Итак, близорукий человек носит очки с оптической силой, например, – 0,5 дптр, -2 дптр (рассеивающие линзы). Дальнозорким людям врачи назначают собирающие линзы. Их оптическая сила положительна, например, + 0,5 дптр, + 3 дптр.

С возрастом способность к аккомодации у глаза ослабевает. Мышцам труднее сжимать хрусталик, и поэтому пожилые люди становятся дальнозоркими.

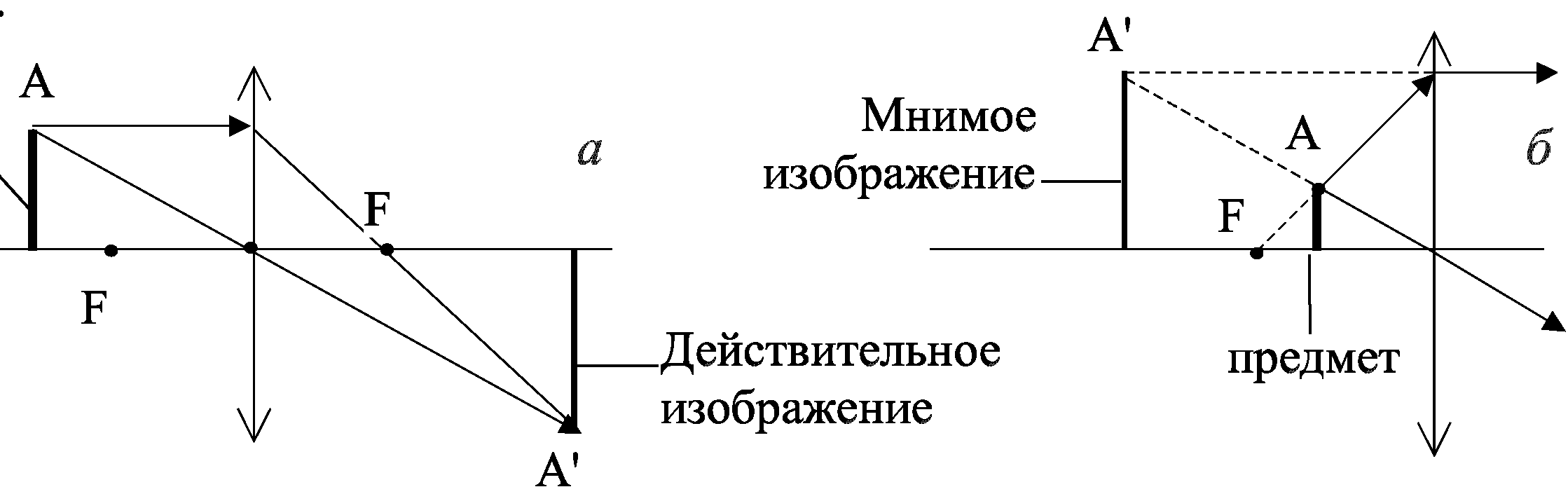
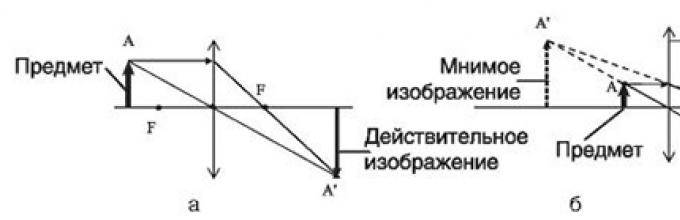
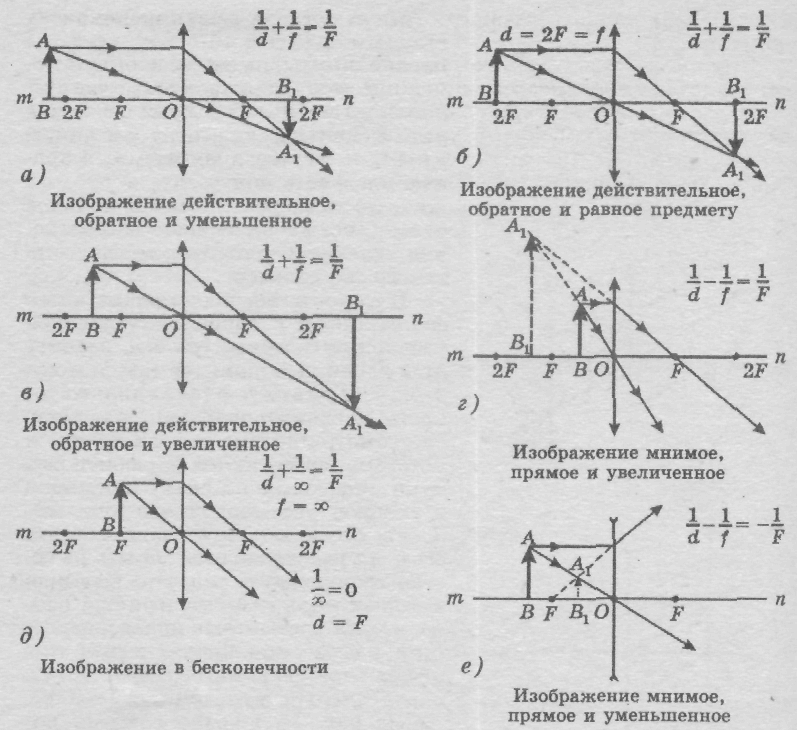
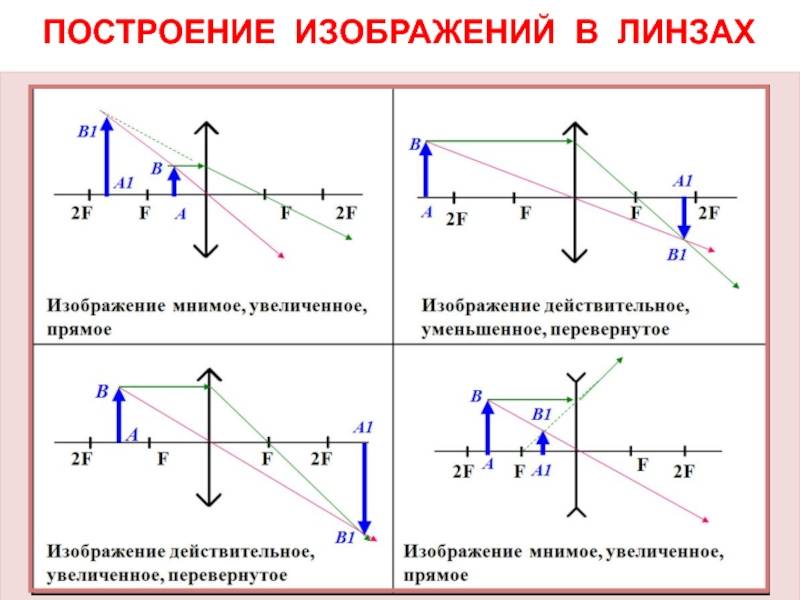
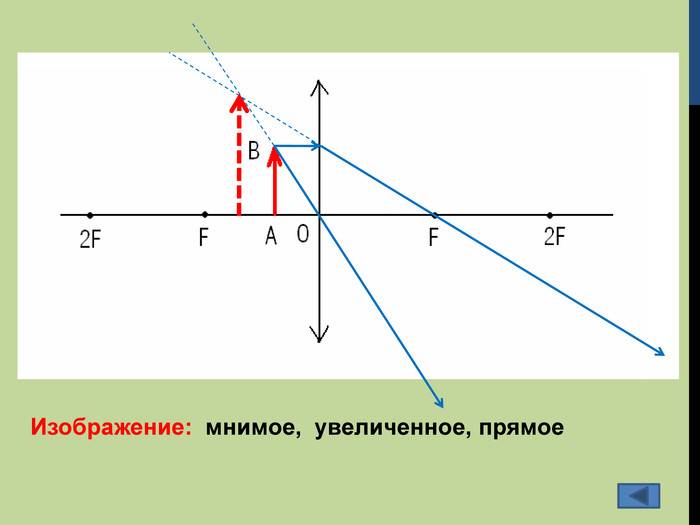
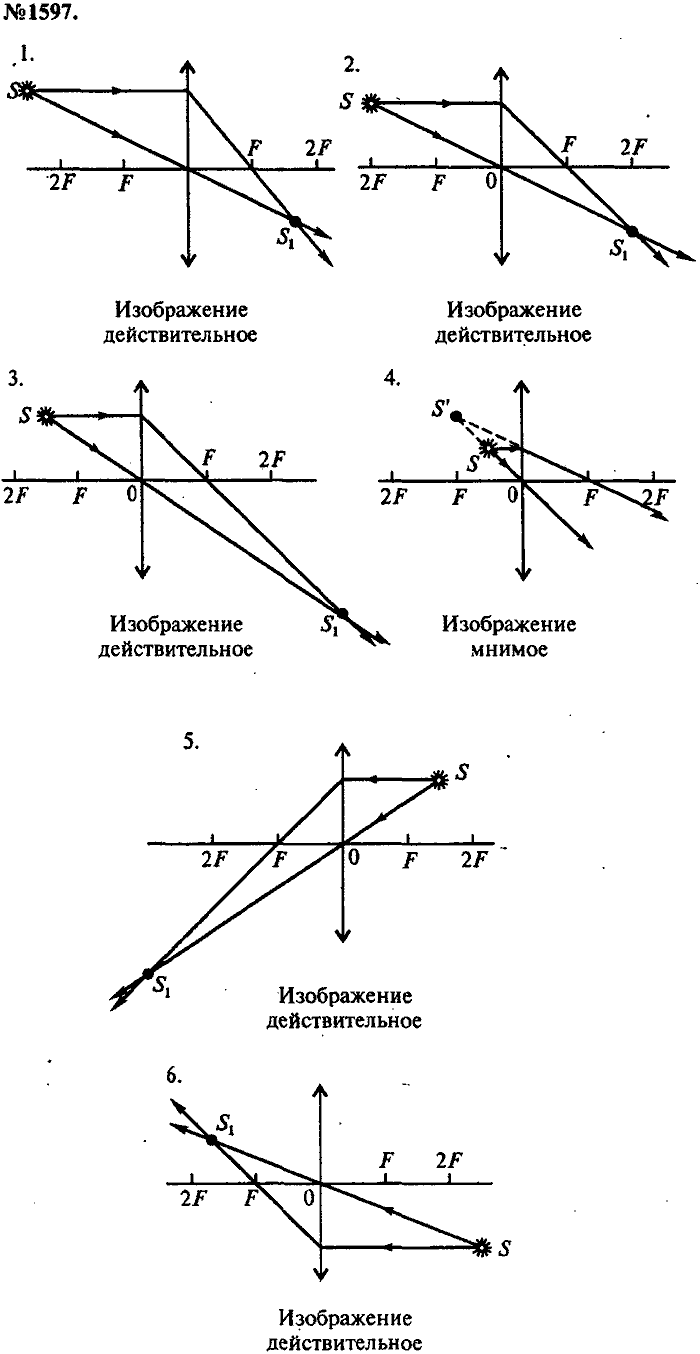
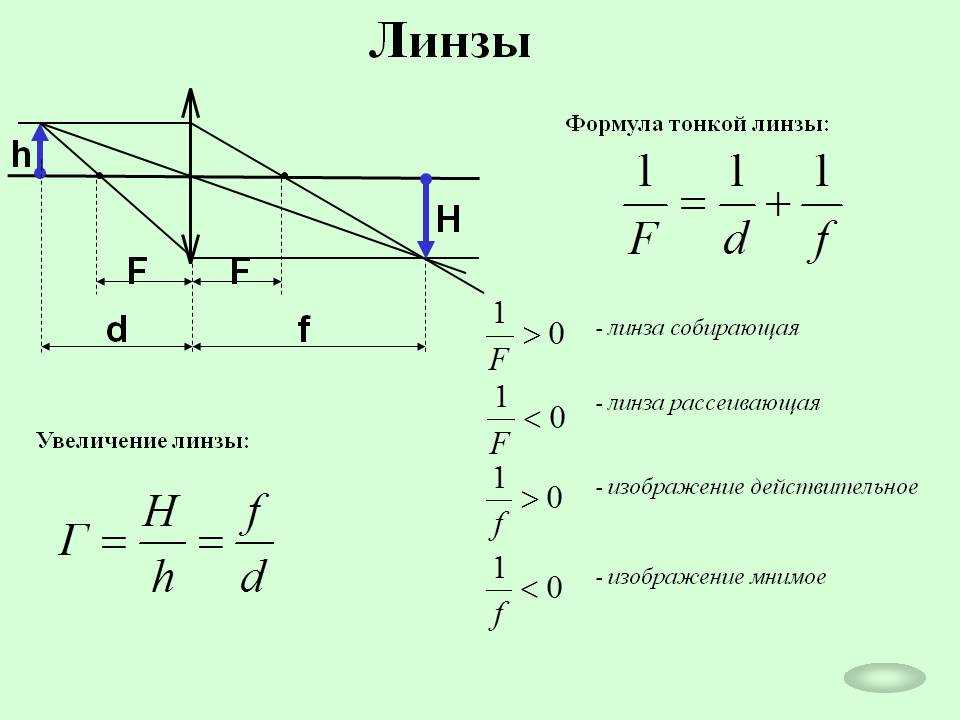
Изображения, даваемые собирающей линзой

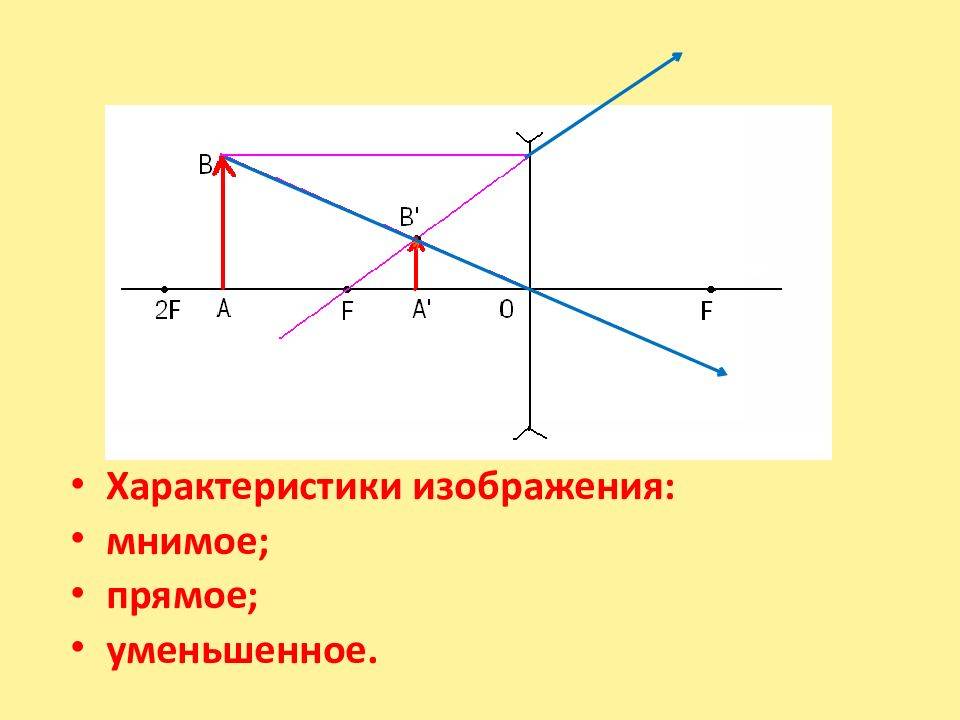
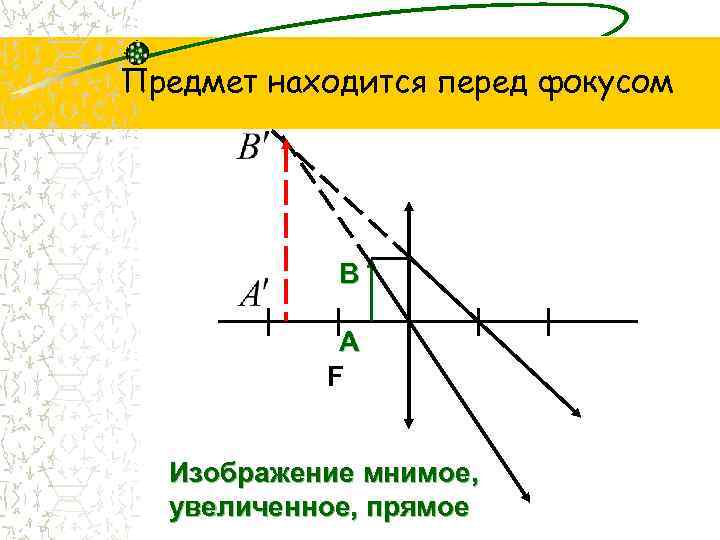
1. Предмет находится между собирающей линзой и фокусом (0

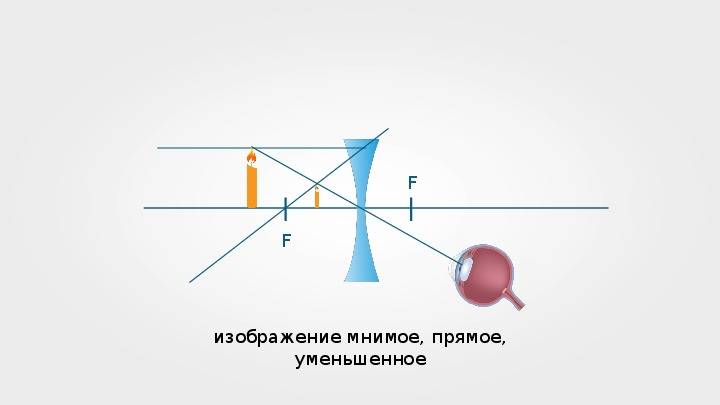
Если расположить свечу между фокусом линзы и самой линзой, то с той же стороны линзы, где находится свеча, мы сможем увидеть увеличенное изображение свечи – её прямое изображение.

Чтобы построить изображение предмета, находящегося между фокусом и собирающей линзой, нужно воспользоваться следующей схемой для каждой точки, которую мы хотим отобразить.

Проводим два луча: один идёт через центр линзы, другой рисуется параллельно оптической оси. Луч, проходящий через центр линзы, не преломляется. Луч, который идёт параллельно оптической оси, после преломления в линзе, пройдёт через фокус.

Мы берём именно эти два луча, т.к. точно известно их поведение при работе с линзами.

Само изображение за линзой не может получится, т.к. эти два луча не пересекаются.

Изображение будет получатся на стороне предмета в точке пересечения продолжений этих двух лучей.

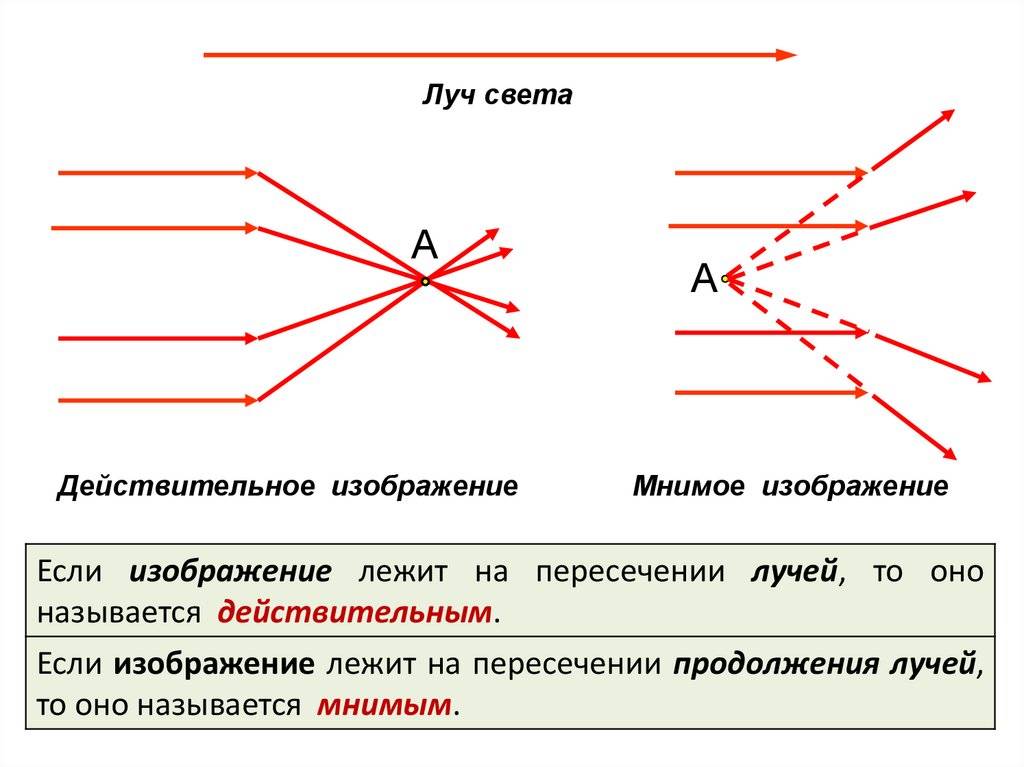
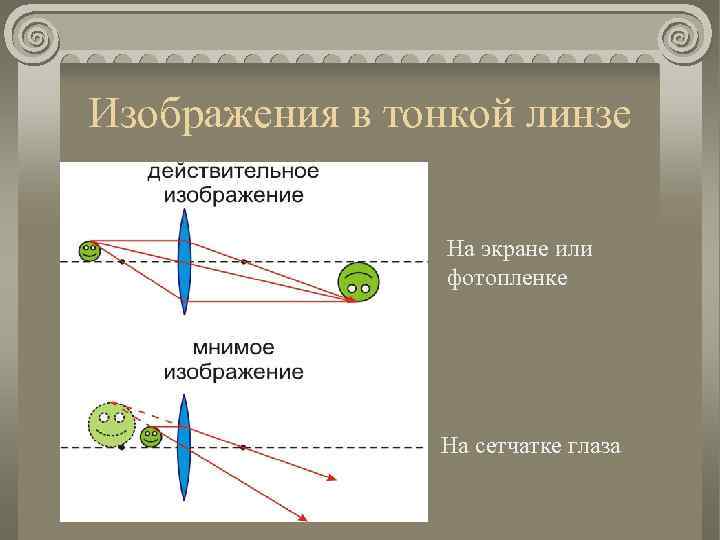
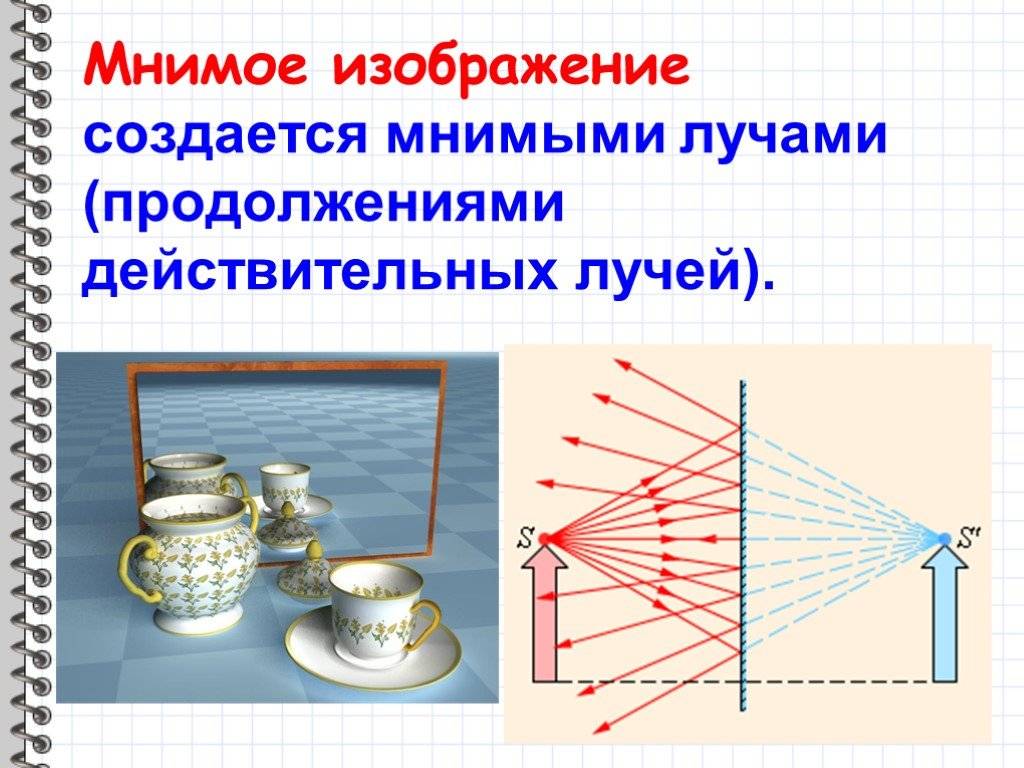
Изображение, которое получается в результате пересечения продолжений расходящихся лучей за линзой, называется мнимым. Изображение, называется действительным, если оно получено в результате пересечения реальных преломлённых лучей. Действительное изображение может быть получено на экране.

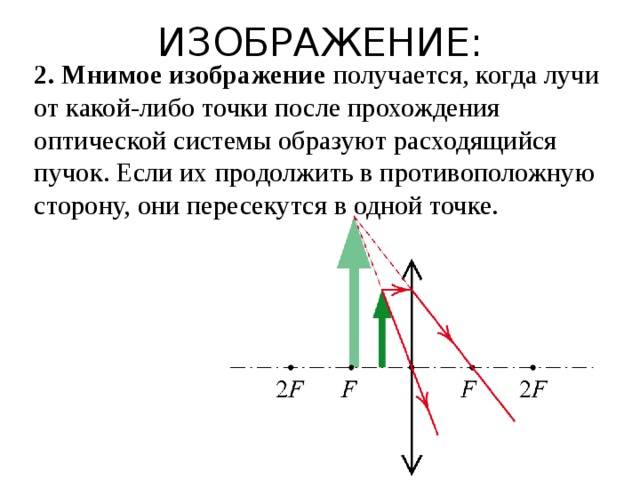
Мнимое изображение – это оптическое изображение предмета, создаваемое расходящимся пучком лучей, прошедшим оптическую систему, если мысленно продолжить их в обратном направлении до пересечения. В отличие от действительного, мнимое изображение нельзя получить на экране или фотоплёнке.

Схематично можно изобразить построение предмета, находящегося между фокусом и линзой (0

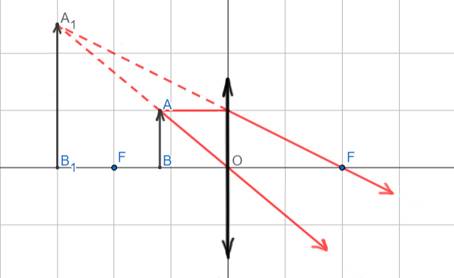
Изображение получается прямым (не перевернутым), мнимым, увеличенным.

2. Предмет находится в фокусном расстоянии (d = F).

Когда предмет находится в фокусе собирающей линзы, лучи света, о которых мы говорили ранее, исходящие из каждой точки предмета, становятся параллельными, после прохождения через линзу. А значит, они не пересекаются между собой, и не создают изображения. Вместо этого, лучи расходятся и создают бесконечно удаленное изображение, которое на самом деле не существует.

Изображения нет.

3. Предмет находится между фокусом и двойным фокусом (F

От каждой точки предмета рисуют два луча, один луч идет параллельно оптической оси и после преломления проходит через фокус линзы, а другой луч идет через центр линзы и не преломляется. Точка пересечения этих двух лучей будет точкой изображения.

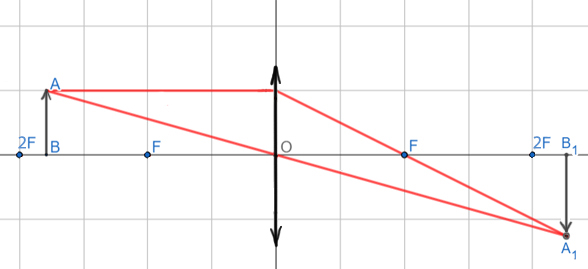
Изображение получается действительным, увеличенным, перевёрнутым.

Изображение получается за двойным фокусным расстоянием.

4. Предмет находится на двойном фокусном расстоянии (d = 2F).

От каждой точки предмета изобразим два луча. Один луч направлен параллельно оптической оси и после прохождения через линзу пройдет через фокус. Второй луч идет через центр линзы и не преломляется. Точка, где эти два луча пересекаются после прохождения через линзу, является изображением данной точки предмета.

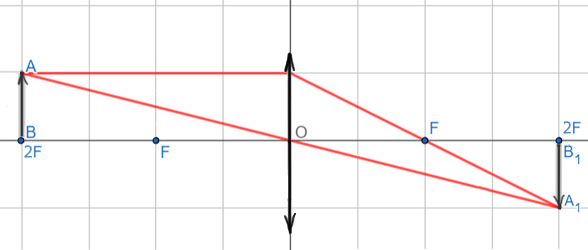
Изображение получается действительным, перевёрнутым, в натуральную величину.

Изображение получается на двойном фокусном расстоянии по ту сторону линзы от предмета.

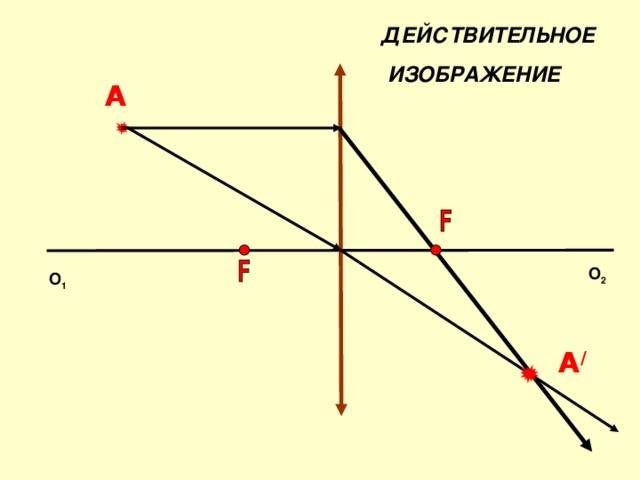
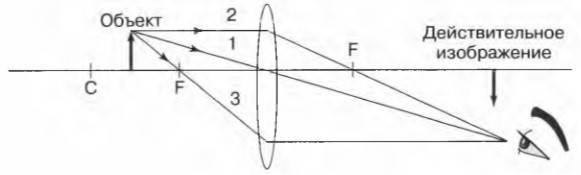
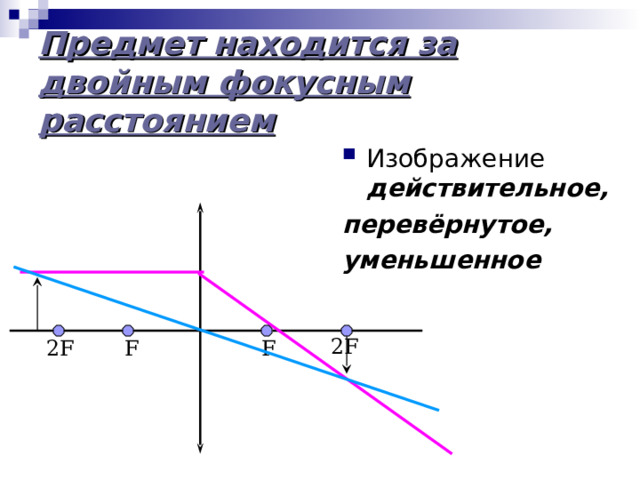
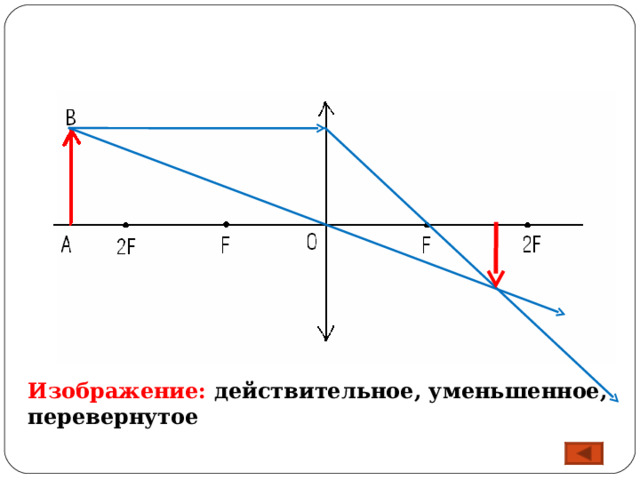
5. Предмет находится от собирающей линзы дальше, чем 2F (d > 2F).

Для построения изображения каждой точки предмета необходимо провести два луча: луч, параллельный оптической оси и проходящий после преломления через фокус линзы, и луч, идущий через центр линзы без преломления. Точка пересечения этих лучей определяет положение изображения.

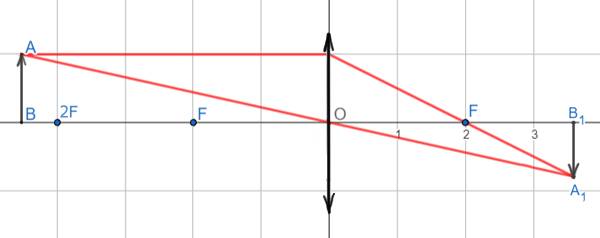
Изображение получается действительным, перевёрнутым, уменьшенным.

Сравнение

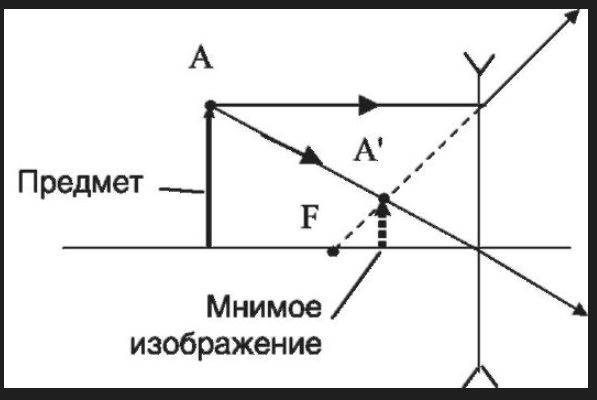
Чтобы разобраться, в чем состоит отличие действительного изображения от мнимого, рассмотрим два рисунка. Вот первый из них:

Здесь точечный источник обозначен буквой A. Он распространяет расходящиеся лучи. На определенном расстоянии расположена некоторая оптическая система (L). Лучи проходят через эту преломляющую среду, меняют свое направление и устремляются к точке A1. Именно она и является действительным, то есть образованным самими лучами, изображением источника A.

Теперь второй случай:

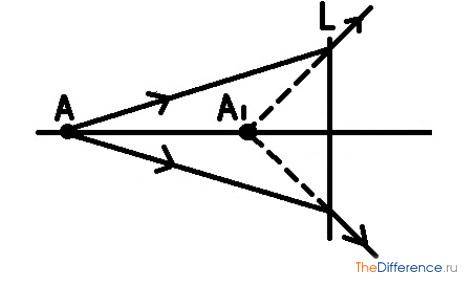
Снова имеем источник света A. Лучи от него движутся к системе L и тоже меняют направление. Только теперь они расходятся. А изображение при этом формируется в месте, где могли бы пересекаться лучи, перемещаясь в обратную сторону (их так называемое продолжение отмечено пунктиром). Точка A1 – мнимое, не созданное непосредственно лучами, изображение.

Какие оптические приборы или предметы позволяют наблюдать каждый из вариантов? В случае с действительным изображением это, скажем, собирающая линза. А с мнимым – лупа, обычное ровное зеркало.

В чем разница между действительным и мнимым изображением еще? В том, что первое из них нельзя увидеть просто «в воздухе». Здесь требуется проекция на поверхность, размещенную в плоскости пересечения прошедших через оптическую среду лучей, например на экран или фотоматрицу. Мнимое изображение зарегистрировать таким образом нельзя. Но его можно просто увидеть или сфотографировать.

Действительное изображение

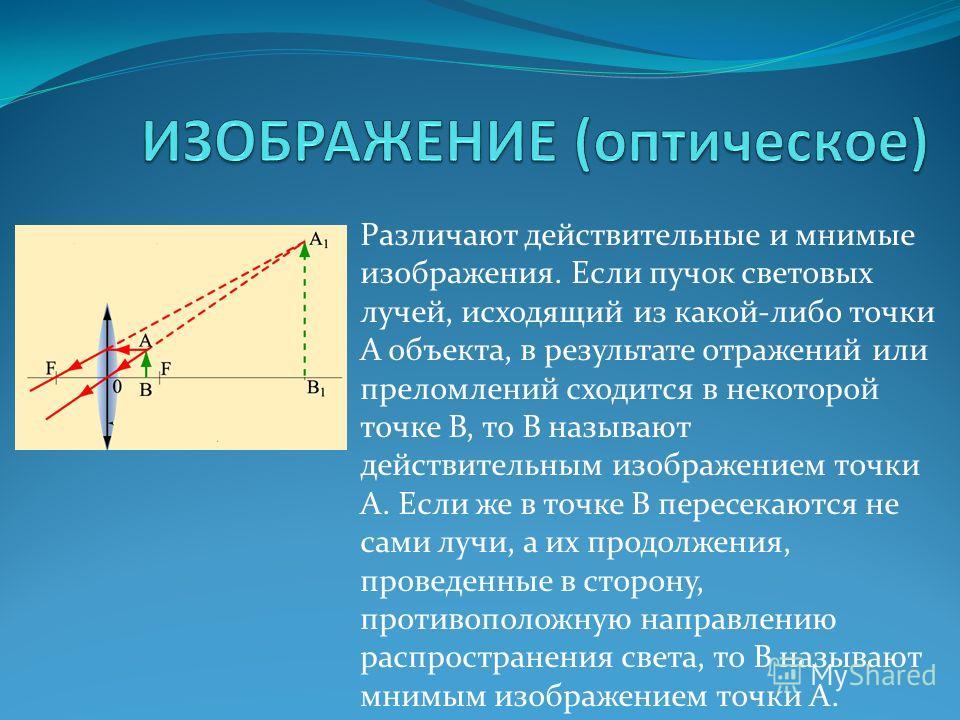
Опти́ческое изображе́ние
– картина, получаемая в результате прохождения через оптическую систему световых лучей, распространяющихся от объекта, и воспроизводящая его контуры и детали.

На практике часто меняют масштаб изображения предметов и проецируют его на какую-либо поверхность.

Соответствие объекту достигается, когда каждая его точка изображается точкой, хотя бы приблизительно. При этом различают два случая: действительное изображение и мнимое изображение.

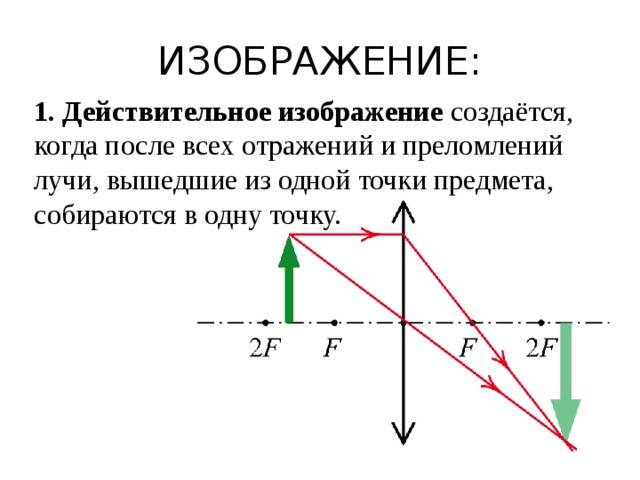
Действительное изображение
создаётся, когда после всех отражений и преломлений лучи, вышедшие из одной точки предмета, собираются в одну точку.

Действительное изображение нельзя видеть непосредственно, но можно увидеть его проекцию, просто поставив рассеивающий экран. Действительное создаётся такими оптическими системами, как объектив (например, кинопроектора или фотоаппарата) или одна положительная линза .

Мнимое изображение
– такое, которое можно видеть глазом. При этом каждой точке предмета соответствует выходящий из оптической системы пучок лучей, которые, если бы продолжить их обратно прямыми линиями, сошлись бы в одной точке; возникает видимость, что пучок выходит именно оттуда. Мнимое изображение создаётся такими оптическими системами, как бинокль , микроскоп , отрицательная или положительная линза (лупа), а также плоское зеркало.

Во всякой реальной оптической системе неизбежно присутствуют аберрации , в результате чего лучи (или их продолжения) не сходятся идеально в одной точке, и кроме того, максимально близко сходятся не совсем там, где нужно. Изображение получается несколько размытым и геометрически не полностью подобным предмету; возможны и другие дефекты.

Пучок лучей, который расходится из одной точки или сходится в ней, называется гомоцентрическим. Ему соответствует сферическая световая волна. Задача большинства оптических систем — преобразовывать расходящиеся гомоцентрические пучки в гомоцентрические же, тем самым создавая мнимое или действительное изображение, чаще всего, в другом масштабе по отношению к предмету.

Стигматическое изображение (от др.-греч. στίγμα

– укол, рубец) – оптическое изображение, каждая точка которого соответствует одной точке изображаемого оптической системой объекта.

Стигматическое изображение не обязательно геометрически подобно изображаемому объекту, но если оно подобно, такое изображение называется идеальным. Это возможно лишь при условии, что в оптической системе отсутствуют или устранены все аберрации , и что возможно пренебречь волновыми свойствами света . Оптическую систему, которая создаёт идеальное изображение, называют идеальной оптической системой. Идеальными можно приближённо считать центрированные системы, в которых изображение получается с помощью монохроматических и параксиальных пучков света.

Формирование действительного и мнимого изображения

Действительное изображение – это изображение, которое образуется при скрещении лучей света на оптической системе и может быть поймано на экране или фотопластинке. Оно является настоящей копией изображаемого предмета и имеет все его характеристики – форму, размеры, цвет и т.д.

Действительное изображение образуется на определенном расстоянии от оптической системы, которое называется фокусным расстоянием. В зависимости от типа оптической системы – линзы или зеркала – действительное изображение может быть прямым или перевернутым.

Мнимое изображение – это изображение, которое образуется при prolongatio лучей света на оптической системе и не может быть поймано на экране или фотопластинке. Оно является иллюзорным, виртуальным отражением изображаемого предмета.

Мнимое изображение образуется там, где лучи света, падающие на оптическую систему, расходятся или продолжают двигаться параллельно друг другу. Такое изображение не может быть фокусировано и, следовательно, не может быть сфокусировано на экране или фотопластинке.

Различие между действительным и мнимым изображениями играет важную роль в оптике и визуализации. Знание о том, как образуется и распространяется свет, позволяет нам понять, как работают оптические приборы, такие как микроскопы, телескопы и камеры, а также позволяет оптимизировать процесс формирования изображений в фотографии и видео.

4.6.6 Рассеивающая линза: мнимое изображение точки






	F A0

Рис. 4.50. Мнимое изображение точки S в рассеивающей линзе

SAO S0
A0
O; SXS0

OP S0
;

SS0
+ S0
O

b A0
O S0
O

Рис. 4.52. Построение изображения точки S, лежащей на главной оптической оси

Соотношение (4.18
) даёт нам ещё один вариант формулы линзы. Сначала перепишем:

а потом разделим обе части полученного равенства на a:

Оптическое изображение воспроизводит контуры и детали этого объекта в виде распределения освещённости .

На практике часто меняют масштаб изображения предметов и проецируют его на какую-либо поверхность.

См. также

Wikimedia Foundation
.
2010
.

Мнимая единица
Мнимая оборона

Смотреть что такое “Мнимое изображение” в других словарях:

МНИМОЕ ИЗОБРАЖЕНИЕ
– (см. ИЗОБРАЖЕНИЕ ОПТИЧЕСКОЕ). Физический энциклопедический словарь. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983. МНИМОЕ ИЗОБРАЖЕНИЕ … Физическая энциклопедия

МНИМОЕ ИЗОБРАЖЕНИЕ
Большой Энциклопедический словарь

МНИМОЕ ИЗОБРАЖЕНИЕ
– см … Большая политехническая энциклопедия

мнимое изображение
– см. Изображение оптическое. * * * МНИМОЕ ИЗОБРАЖЕНИЕ МНИМОЕ ИЗОБРАЖЕНИЕ, см. Изображение оптическое (см. ИЗОБРАЖЕНИЕ ОПТИЧЕСКОЕ) … Энциклопедический словарь

мнимое изображение
– menamasis vaizdas statusas T sritis fizika atitikmenys: angl. apparent image; virtual image vok. scheinbares Bild, n; virtuelles Bild, n rus. мнимое изображение, n pranc. image virtuelle, f … Fizikos terminų žodynas

Мнимое изображение
– предмета (воспринимается глазом как предмет) образуется пересечениями геометрических продолжений световых лучей, прошедших через оптическую систему, в направлениях, обратных действительному ходу этих лучей. Подробнее см. Изображение… … Большая советская энциклопедия

МНИМОЕ ИЗОБРАЖЕНИЕ
– см. Изображение оптическое …

ИЗОБРАЖЕНИЕ ОПТИЧЕСКОЕ
– ИЗОБРАЖЕНИЕ ОПТИЧЕСКОЕ, изображение объекта при помощи оптического прибора. Действительное изображение формируется совокупностью точек, в которых сходятся лучи света, прошедшие через оптический прибор. Через точки, образующие мнимое изображение,… … Научно-технический энциклопедический словарь

ИЗОБРАЖЕНИЕ ОПТИЧЕСКОЕ
– изображение объекта, получаемое в результате действия оптич. системы на световые лучи, испускаемые или отражаемые объектом. И.о. воспроизводит контуры и детали объекта с нек рыми искажениями (аберрациями оптич. систем). Различают действит. и… … Естествознание. Энциклопедический словарь

Изображение оптическое
– Оптическое изображение картина, получаемая в результате прохождения через оптическую систему световых лучей, распространяющихся от объекта, и воспроизводящая его контуры и детали. На практике часто меняют масштаб изображения предметов и… … Википедия

3.
a > 2f. В этом случае из формулы линзы следует, что b 4.44
).





Рис. 4.44. a > 2f: изображение действительное, перевёрнутое, уменьшенное

Данная ситуация является обычной для многих оптических приборов: фотоаппаратов, биноклей, телескопов словом, тех, в которых получают изображения удалённых объектов. По мере удаления предмета от линзы его изображение уменьшается в размерах и приближается к фокальной плоскости.

Рассмотрение первого случая a > f нами полностью закончено. Переходим ко второму случаю. Он уже не будет столь объёмным.

4.6.3
Собирающая линза: мнимое изображение точки

Второй случай: a

Рис. 4.45. Случай a

Наряду с лучом SO, идущим без преломления, мы снова рассматриваем произвольный луч SX. Однако теперь на выходе из линзы получаются два расходящихся луча OE и XP . Наш глаз продолжит эти лучи до пересечения в точке S0
.

Теорема об изображении утверждает, что точка S0
будет одной и той же для всех лучей SX, исходящих из точки S. Мы опять докажем это с помощью трёх пар подобных треугольников:

SAO S0
A0
O; SXS0
OP S0
; SXK OP F:

Снова обозначая через b расстояние от S0
до линзы, имеем соответствующую цепочку равенств (вы уже без труда в ней разберётесь):

S0
O S0
S

b A0
O S0
O

Величина b не зависит от луча SX, что и доказывает теорему об изображении для нашего случая a

Если точка S не лежит на главной оптической оси, то для построения изображения S0
удобнее всего брать луч, идущий через оптический центр, и луч, параллельный главной оптической оси (рис.4.46
).

Рис. 4.46. Построение изображения точки S, не лежащей на главной оптической оси

Ну а если точка S лежит на главной оптической оси, то деваться некуда придётся довольствоваться лучом, падающим на линзу наклонно (рис. 4.47
).

Рис. 4.47. Построение изображения точки S, лежащей на главной оптической оси

Соотношение (4.14
) приводит нас к варианту формулы линзы для рассматриваемого случая a

1 a
b
=f
a
;

а затем делим обе части полученного равенства на a:

Сравнивая (4.12
) и (4.16
), мы видим небольшую разницу: перед слагаемым 1=b стоит знак плюс, если изображение действительное, и знак минус, если изображение мнимое.

Величина b, вычисляемая по формуле (4.15
), не зависит также от расстояния SA между точкой S и главной оптической осью. Как и выше (вспомните рассуждение с точкой M), это означает, что изображением отрезка SA на рис.4.47
будет отрезок S0
A0
.

Свойства

Стигматическое изображение (от др.-греч. στίγμα

Хотя глазом человека действительные и мнимые изображения воспринимаются одинаково, при формировании действительного изображения пересечение лучей реальное, и эти реальные лучи могут подействовать, например, на фотоплёнку, вызвав в ней химические преобразования, или быть зафиксированы фотоэлементом.