Чем отличается цифра от числа

Что такое число?

Число считается одним из главных понятий в математике. Его используют для сравнения, нумерации, описания количественной характеристики. Таким образом, числа обозначаются при помощи цифр, а также математических символов («плюс», «минус», «скобки» и др.).

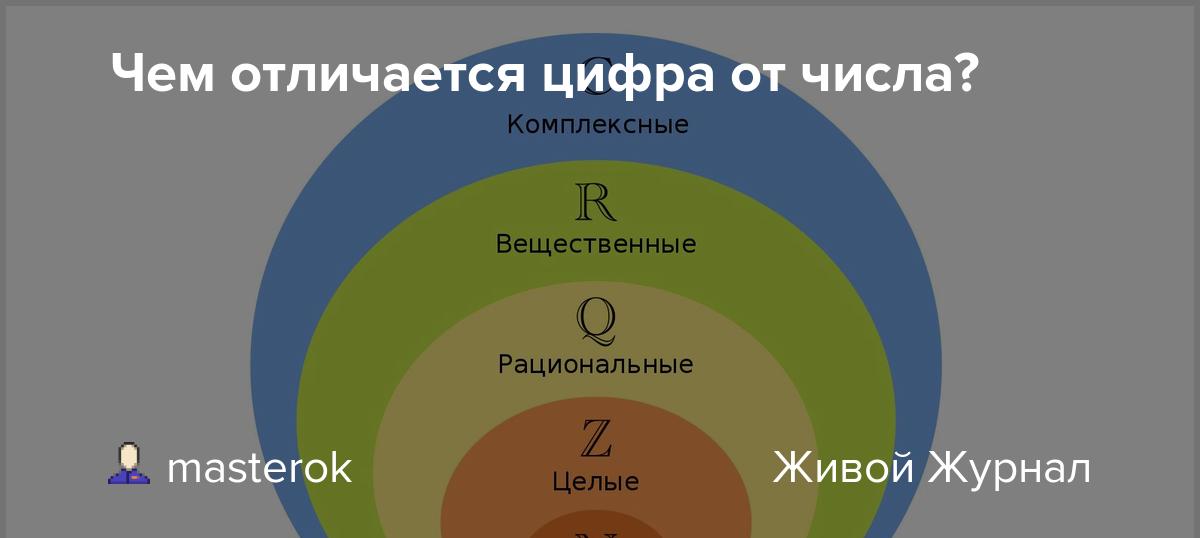
Иерархия чисел

Необходимость вести счет чего-либо возникла еще у первобытных людей, и понятие числа постепенно становилось все сложнее. С развитием науки оно обрело еще более глубокий и важный смысл. Выделяют несколько числовых множеств:

натуральные – используются при естественном счете (от единицы и до бесконечности, а иногда и от ноля);
целые – объединение натуральных, отрицательных чисел и ноля;
рациональные – дроби;
действительные – представляют собой расширение множества рациональных чисел;
комплексные – расширение множества действительных чисел.

Отличия числа от цифры

С числами можно проводить различные математические действия. С цифрами такого делать нельзя.
Число может быть отрицательным, дробным, в отличие от цифр.
Количество арабских цифр всего 10 (римских — 7), а чисел — бесконечное множество, т.к. они состоят из цифр.

Надеюсь, что теперь вам всё понятно, и вы сможете без труда объяснить даже ребёнку, чем отличается число от цифры.

На уроках математики в начальной школе используется очень полезное упражнение. Детей просят дать характеристику числу. Другими словами рассказать о числе все, что знаешь. Не всем детям это задание даётся легко. Чтобы его выполнить пригодятся вышеописанные знания и не только.

Буквенные выражения

Задача

1) 3 тетради: 2 x 3 + 5;

2) 6 тетрадей: 2 x 6 + 5;

3) 10 тетрадей: 2 x 10 + 5;

4) n тетрадей: 2 x n + 5.

Выражение 1,2,3 называются числовыми выражениями, а в выражение 4 кроме чисел, соединённых знаками действия, входит буква n.

В названиях арабских чисел каждая цифра принадлежит своему разряду, а каждые три цифры образуют класс. Таким образом, последняя цифра в числе обозначает количество единиц в нем и называется, соответственно, разрядом единиц. Следующая, вторая с конца, цифра обозначает десятки (разряд десятков), и третья с конца цифра указывает на количество сотен в числе – разряд сотен. Дальше разряды точно также по очереди повторяются в каждом классе, обозначая уже единицы, десятки и сотни в классах тысяч, миллионов и так далее. Если число небольшое и в нем нет цифры десятков или сотен, принято принимать их за ноль. Классы группируют цифры в числах по три, нередко в вычислительных приборах или записях между классами ставится точка или пробел, чтобы визуально разделить их. Это сделано для упрощения чтения больших чисел. Каждый класс имеет свое название: первые три цифры – это класс единиц, далее идет класс тысяч, затем миллионов, миллиардов (или биллионов) и так далее.

Поскольку мы пользуемся десятичной системой исчисления, то основная единица измерения количества – это десяток, или 10 1
. Соответственно с увеличением количества цифр в числе, увеличивается и количество десятков 10 2
,10 3
,10 4
и т.д. Зная количество десятков можно легко определить класс и разряд числа, например, 10 16
– это десятки квадриллионов, а 3×10 16
– это три десятка квадриллионов. Разложение чисел на десятичные компоненты происходит следующий образом – каждая цифра выводится в отдельное слагаемое, умножаясь на требуемый коэффициент 10 n
, где n
– положение цифры по счет слева направо.
Например:
253 981=2×10 6 +5×10 5 +3×10 4 +9×10 3 +8×10 2 +1×10 1

Также степень числа 10
используется и в написании десятичных дробей : 10 (-1)
– это 0,1
или одна десятая. Аналогичным образом с предыдущим пунктом, можно разложить и десятичное число, n
в таком случае будет обозначать положение цифры от запятой справа налево, например:
0,347629= 3×10 (-1) +4×10 (-2) +7×10 (-3) +6×10 (-4) +2×10 (-5) +9×10 (-6)

Названия десятичных чисел. Десятичные числа читаются по последнему разряду цифр после запятой, например 0,325
– триста двадцать пять тысячных, где тысячные – это разряд последней цифры 5
.

Системы счисления

Система счисления – это некий вариант представления чисел.

К примеру, представьте, что перед вами лежит несколько яблок. Вы хотели бы узнать, сколько яблок лежат на столе? Для этого вы могли бы считать, загибая пальцы рук или делать зарубки на дереве. А могли бы вы и представить, что десять яблок – это одна корзинка, а одно яблоко – это одна спичка. Спички по ходу счета выкладывать на столе под одной.

В первом варианте подсчета число получилось в виде строки из зарубок на дереве (или загнутых пальцев рук), а во втором варианте подсчета – это был набор из корзинок и спичек. Слева должны быть емкости, а справа — спички.

Системы счисления бывают двух видов:

Позиционные.
Непозиционные.

Позиционные системы счисления бывают:

Однородными.
Смешанными.

Непозиционной называют такую систему счисления, в которой цифра в числе соотносится с такой величиной, которая не зависит от ее разряда. Поэтому, если у вас пять зарубок, то число будет равно пяти. Ибо каждой зарубке будет соответствовать одно яблоко.

Позиционной системой счисления является та, в которой цифра в числе будет зависеть от ее разряда.

Та система счисления, к которой мы привыкли – это десятичная система счета. Она позиционная.

Когда наши предки начали учиться считать, у них появилась идея записывать числа. изначально они использовали те самые зарубки на деревьях или камнях, где каждая черточка обозначала какой-либо предмет (одно яблоко, к примеру). Именно так и была изобретена единичная система счисления.

Цифры в повседневной жизни: их роль и значение

Роль цифр в нашей повседневной жизни

Цифры используются в различных областях нашей жизни, начиная от ежедневных дел и заканчивая сложными научными исследованиями. В повседневной жизни мы сталкиваемся с цифрами во многих ситуациях: при покупках, в банковской деятельности, при подсчете времени, в спорте, в медицине и т.д. Цифры помогают нам делать точные расчеты, оценивать и представлять информацию в удобном и понятном виде.

Значение цифр в современном мире

Цифры имеют огромное значение в современном мире. Они позволяют нам измерять, сравнивать, анализировать и прогнозировать различные явления и процессы. Цифры помогают нам понять и оценить масштабы событий, развивать науку и технологии, управлять экономикой и многое другое. Без цифр было бы невозможно проводить точные измерения и делать рациональные решения, основанные на фактических данных.

Примеры использования цифр в повседневной жизни:

Сфера
Примеры использования цифр

Торговля
Цены на товары, скидки, количество продаж

Финансы
Банковские счета, кредиты, инвестиции

Медицина
Измерение веса, давления, температуры

Спорт
Результаты соревнований, время, рекорды

Образование
Оценки, прогресс, статистика успеваемости

Зачем нам нужно знать разницу между числами и цифрами?

Разница между числами и цифрами может показаться незначительной, но на самом деле эти термины имеют разные значения и применяются в разных контекстах. Понимание этой разницы может помочь ребенку развить не только математические навыки, но и общую логику и понимание окружающего мира.

Число — это абстрактный понятий, которое обозначает количество или порядок объектов. Например, число 5 может означать пять яблок или пятерых детей.

Цифра, с другой стороны, является символом, используемым для обозначения числа. Это может быть обычное десятичное число (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), а также другие числовые символы, такие как римские цифры (I, V, X, L, C, D, M), двоичные числа (0, 1), восьмеричные числа (0, 1, 2, 3, 4, 5, 6, 7) и шестнадцатеричные числа (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).

Знание разницы между числами и цифрами может быть полезно в решении математических задач и в повседневной жизни. Например, чтобы посчитать общую сумму в магазине, нужно использовать цифры, чтобы обозначить цены товаров. А чтобы понять, сколько яблок нужно купить, нужно использовать числа.

Помимо математической пользы, разница между числами и цифрами помогает развить у ребенка абстрактное мышление и способность анализировать информацию

Это также может улучшить их навыки коммуникации, так как правильное использование чисел и цифр важно для точности и ясности

В целом, осознание разницы между числами и цифрами помогает ребенку развить фундаментальные математические навыки и логическое мышление, что полезно для их дальнейшего образования и успеха в жизни.

Чем отличается цифра от числа?

Таким образом, цифра – это просто знак, символ, который можно сравнить с буквами в словах. Число же является математическим понятием, количественным показателем, и для его графического изображения используются именно цифры. Рассматривая статистики, графики, отчеты – любые количественные данные, мы видим числа, а не цифры.

Цифры числовой системы майя с индийско-арабскими эквивалентами

Разнообразие чисел довольно большое. Они могут быть целыми, четными, нечетными, положительными, отрицательными и т.д. Также не существует какого-либо последнего числа – всегда будет то, что больше него. Количество цифр ограничено десятью знаками: от 0 до 9. Сравнивать между собой можно только числа, а не цифры.

По материалам: kipmu.ru

Таблица названий больших чисел, разрядов и классов

1-й класс единицы	1-й разряд единицы 2-й разряд десятки 3-й разряд сотни	1 = 10 0 10 = 10 1 100 = 10 2
2-й класс тысячи	1-й разряд единицы тысяч 2-й разряд десятки тысяч 3-й разряд сотни тысяч	1 000 = 10 3 10 000 = 10 4 100 000 = 10 5
3-й класс миллионы	1-й разряд единицы миллионов 2-й разряд десятки миллионов 3-й разряд сотни миллионов	1 000 000 = 10 6 10 000 000 = 10 7 100 000 000 = 10 8
4-й класс миллиарды	1-й разряд единицы миллиардов 2-й разряд десятки миллиардов 3-й разряд сотни миллиардов	1 000 000 000 = 10 9 10 000 000 000 = 10 10 100 000 000 000 = 10 11
5-й класс триллионы	1-й разряд единицы триллионов 2-й разряд десятки триллионов 3-й разряд сотни триллионов	1 000 000 000 000 = 10 12 10 000 000 000 000 = 10 13 100 000 000 000 000 = 10 14
6-й класс квадриллионы	1-й разряд единицы квадриллионов 2-й разряд десятки квадриллионов 3-й разряд десятки квадриллионов	1 000 000 000 000 000 = 10 15 10 000 000 000 000 000 = 10 16 100 000 000 000 000 000 = 10 17
7-й класс квинтиллионы	1-й разряд единицы квинтиллионов 2-й разряд десятки квинтиллионов 3-й разряд сотни квинтиллионов	1 000 000 000 000 000 000 = 10 18 10 000 000 000 000 000 000 = 10 19 100 000 000 000 000 000 000 = 10 20
8-й класс секстиллионы	1-й разряд единицы секстиллионов 2-й разряд десятки секстиллионов 3-й разряд сотни секстиллионов	1 000 000 000 000 000 000 000 = 10 21 10 000 000 000 000 000 000 000 = 10 22 1 00 000 000 000 000 000 000 000 = 10 23
9-й класс септиллионы	1-й разряд единицы септиллионов 2-й разряд десятки септиллионов 3-й разряд сотни септиллионов	1 000 000 000 000 000 000 000 000 = 10 24 10 000 000 000 000 000 000 000 000 = 10 25 100 000 000 000 000 000 000 000 000 = 10 26
10-й класс октиллион	1-й разряд единицы октиллионов 2-й разряд десятки октиллионов 3-й разряд сотни октиллионов	1 000 000 000 000 000 000 000 000 000 = 10 27 10 000 000 000 000 000 000 000 000 000 = 10 28 100 000 000 000 000 000 000 000 000 000 = 10 29

Значение чисел в различных культурах

Числа играют важную роль в различных культурах и имеют особое значение, которое может быть связано с историей, религией или повседневной жизнью народов. В каждой культуре существуют свои особенности и традиции, связанные с числами.

Например, в китайской культуре число 8 считается счастливым и приносящим удачу. Оно звучит похоже на слово, означающее процветание и богатство. Поэтому многие китайские бизнесмены и предприниматели предпочитают номера машин и телефонов, содержащие несколько восьмерок.

Символика чисел также играет важную роль в христианской культуре. Например, число 7 считается священным и символизирует полноценность и совершенство. Это число упоминается в Библии во многих контекстах, от семи дней творения мира до семи духов перед престолом Божьим. В христианской иконографии семь часто используется для изображения семи сакраментов и семи добродетелей.

В индийской культуре число 108 имеет особое значение и используется в множестве ритуалов и традиций. Оно считается священным числом и символизирует гармонию и совершенство. Известно, что в традиционном индийском искусстве, таком как йога и медитация, используются мантры с повторением 108 раз.

В японской культуре число 4 считается несчастливым, так как произношение его похоже на слово, означающее смерть. Поэтому четвертых этажей в зданиях обычно нет, пропускают номера 4 в регистрационных номерах машин и предпочитают избегать его использования в речи.
В американской культуре число 13 связано с неудачей и считается несчастливым. Так называемый «черный пятницы 13-го» стал символом неприятностей и неудач. Во многих отелях и зданиях отсутствует 13-й этаж, пропускают этот номер в некоторых ряду.
В русской культуре число 3 считается магическим и счастливым. Многие сказки и пословицы содержат тройку элементов или повторяются три раза. Также тройка считается символом счастья и удачи.

Это лишь небольшой обзор значения чисел в различных культурах. При изучении разных культур полезно узнать больше о цифрах и их символике, чтобы понять народные традиции и обычаи.

Гипотезы

Сегодня нет однозначного мнения насчет формирования написания арабских цифр. Ни один ученый не знает, почему определенные цифры выглядят именно таким образом, а не как-то по-другому. Чем руководствовались древние ученые, придавая цифрам формы? Одной из самых правдоподобных гипотез является та самая, с количеством углов.

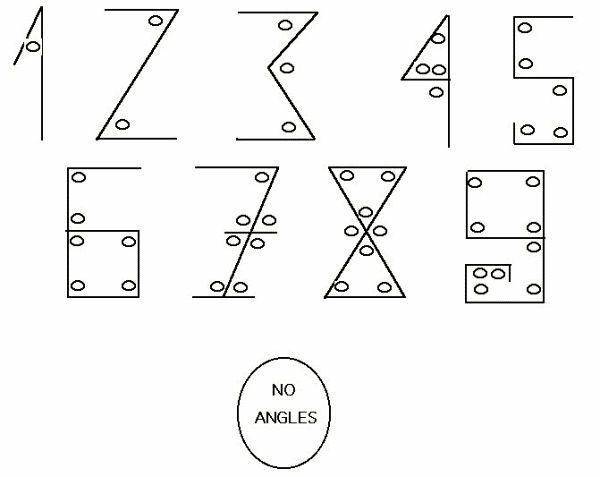
Конечно, с течением времени все углы у цифр сглаживались, они постепенно приобрели привычный для современного человека облик. И уже огромное число лет арабские цифры по всему миру используются для обозначения чисел. Удивительно, что всего десятью символами можно передать невообразимо большие значения.

Число и десятичная система счисления

Числа отличаются от цифр тем, что могут состоять как из одной, так и из нескольких цифр, записанных подряд. Десятичная система счисления – это позиционная система. Значение цифры зависит от места (позиции), которое она занимает в числе. Цифры – это тоже числа, но состоящие из одной цифры, которая занимает позицию в разряде единиц. Если необходимо записать число, следующее по порядку за 9, то нужно перейти к следующему разряду – разряду десятков.

Таким образом следующим числом будет 10 – один десяток, ноль единиц, 11 – один десяток одна единица, 12 – один десяток две единицы, 25 – два десятка пять единиц и так далее. После числа 99 идет число 100 – одна сотня ноль десятков ноль единиц. Дальше добавляются разряды тысяч, десятков тысяч, сотен тысяч, миллионов и т.д. Таким образом, добавляя слева новые разряды, мы можем пользоваться все большими и большими числами.

Зачем нужно уметь распознавать числа и цифры?

Умение распознавать числа и цифры имеет важное значение для нашей жизни и общения в современном мире. Вот несколько причин, почему это важно:

1.	Понимание количества и измерение. Числа позволяют нам понимать количество объектов или явлений в нашем окружении. Например, мы используем числа для счета денег, расстояния, времени и многого другого. Распознавание цифр позволяет нам с легкостью читать и записывать эти числа.
2.	Коммуникация и обмен информацией. Цифры играют важную роль в нашем общении с другими людьми. Мы используем их в различных ситуациях, например, при обмене номерами телефонов, адресами, пин-кодами и многом другом. Благодаря умению распознавать цифры, мы можем легко и точно понимать и передавать информацию.
3.	Успех в образовании и работе. Знание чисел и умение с ними работать является необходимым навыком для получения образования и достижения успеха в профессиональной сфере. Например, математика — это один из основных предметов в школе, а высокий уровень числовой грамотности может открыть двери к разным карьерным возможностям.
4.	Развитие логического мышления. Распознавание чисел и цифр требует анализа и сопоставления информации. Это помогает развивать логическое мышление и способность решать проблемы. Например, при выполнении математических задач мы применяем логику и абстрактное мышление.

Таким образом, умение распознавать числа и цифры является неотъемлемой частью нашей жизни и помогает нам во многих аспектах, начиная от повседневных задач и окончая достижением карьерных целей. Кроме того, развитие навыков работы с числами и цифрами способствует умственному развитию и помогает нам стать активными участниками современного информационного общества.

По вехам истории

Люди настолько привыкли к цифрам, что даже не задумываются об их важности в жизни. Наверное, многие слышали, что цифры, которые используются, называются арабскими

Некоторым это объяснили в школе, а кто-то узнал случайно. Так почему цифры называются арабскими? Какова их история?

А она является очень запутанной. Нет достоверно точных фактов об их происхождении. Известно точно, что благодарить стоит древних астрономов. Из-за них и их расчетов люди сегодня имеют числа. Астрономы из Индии где-то между II и VI веками познакомились со знаниями греческих коллег. Оттуда была взята шестидесятиричная и круглый нуль. Затем греческая была объединена с китайской десятичной системой. Индусы стали обозначать цифры одним знаком, и их способ быстро разлетелся по всей территории Европы.

Названия и последовательность натуральных чисел от 1 до 20

Числа 1,2,3,4,5,6,7,8,9,0, которые используются при счёте- это натуральные числа. С помощью цифр 0,1,2,3,4,5,6,7,8,9 можно записать натуральное число. Такая запись чисел называется десятичной. В каждом классе присутствует три разряда.

Приведём ниже таблицу разрядов.

Классы Миллиарды
Миллионы
Тысячи
Единицы

Разряд Сотни Десятки Единицы Сотни Десятки Единицы Сотни Десятки Единицы Сотни Десятки Единицы

1-е число 2 0 0 3 2 4 0 6 0 0 8 1

2-е число 4 7 0 0 0 0 2 0 2 3 0 0

3-е число 5 0 0 1 0 0 0 3 1 0 9 0

Вот так читаются некоторые числа:

1) десять миллиардов тридцать два миллиона четыреста шестьдесят девять тысяч восемь;
2) четыреста семьдесят миллиардов сто тридцать тысяч триста;
3) пять миллиардов три миллиона триста десять.

Существуют и такие классы: класс триллионов, класс квадриллионов, класс квинтиллионов.

Как дошкольники могут использовать цифры

Для дошкольников цифры являются первым шагом в изучении математики. Они учатся распознавать и называть цифры, а также использовать их в повседневной жизни. Вот несколько способов, как дошкольники могут использовать цифры:

1. Счет: Дошкольники могут использовать цифры для счета предметов. Например, они могут поставить цифры от 1 до 10 рядом с предметами и сосчитать их.

2. Распознавание: Дошкольники могут использовать цифры для распознавания номеров автобусов, адресов и других значений в повседневной жизни.

3. Игры: Дошкольники могут играть в игры, которые помогают им учиться цифрам. Например, они могут играть в игру «Угадай число», где им нужно угадать число, которое угадывает их друг или родитель.

4. Использование в рисунке: Дошкольники могут использовать цифры для создания простых рисунков. Например, они могут нарисовать фигуры, используя цифры в качестве контуров.

5. Размещение по порядку: Дошкольники могут использовать цифры для расположения предметов в порядке. Например, они могут поставить цифры от 1 до 5 рядом с игрушками, чтобы указать, в каком порядке они должны быть уложены.

Использование цифр — это только начало математического обучения дошкольников. Они также могут учиться сравнивать цифры, складывать и вычитать, и использовать их для измерений. Чем больше они будут учиться и использовать цифры, тем лучше они будут готовы к сложным математическим концепциям в будущем.

Что такое цифра?

Это вопрос, на который мы получаем ответ изначально от родителей, потом от преподавателей в учебных заведениях. Что такое цифра? А из словаря Владимира Даля можно узнать, что цифры — это численные показатели. Именно они представляются символами чисел. Нам известно всего 10 цифр: от нуля до девяти. Из их сочетания получается бесконечность чисел. Какие же существуют цифры?

Арабские. Такими символами мы пользуемся довольно-таки давно. Они возникли в Европе еще в 10-м веке.
Римские. Возникли еще за пять веков до нашей эры и находились в обиходе у племен этрусков, проживавших на Апеннинском полуострове.
Цифры майя. Такие знаки использовались для расчетов в календаре.

Но в современном мире цифра — это не только математический знак, и сегодняшний день существует даже цифровое телевидение, а также существует цифровой формат.

Что такое цифра?

Цифра – это упорядоченная знаковая система, предназначенная для записи чисел. Цифрами считаются только те символы, которые в отдельности обозначают числа. Например, знак “-” хоть и применяется для того, чтобы записать число, но цифрой он не считается. Цифрами считается ряд от 0 до 9. Само слово “цифра” имеет арабские корни и обозначает “ноль” или “пустое место”. Эти символы бывают следующих видов:

Это перечислены самые известные разновидности. В разных языках, например, в древнегреческом, для записи чисел используют буквы. Чаще всего в обиходной речи люди под словом “цифры” подразумевают числа, которыми записываются числовые данные. Следует помнить, что отрицательных, дробных и натуральных цифр не существует.

Привычная нам система исчисления основывается на цифрах арабского происхождения, которые стали известны европейцам в 13-м веке. До этого для записи чисел использовали римские графические символы. Сейчас эту разновидность можно увидеть на циферблате часов, а также в книгах.

Число – это основное математическое понятие. Его используют для:

количественной характеристики;
сравнения;
обозначения нумерации объектов.

Числа записываются цифрами и иногда при помощи символов операций в математике. Они возникли еще в первобытном обществе, когда появилась потребность в счете. Числа бывают:

натуральные – получаются при естественном счете;
целые – получаются при помощи объединения натуральных чисел;
рациональные – имеют вид дроби;
действительные;
комплексные.

Два последних вида чисел имеют важное значение для математического анализа и получаются благодаря расширению рациональных (для действительных) и действительных (для комплексных) чисел. Если в древние времена числа были нужны для перечисления, то с научным прогрессом их значение возросло

Если в древние времена числа были нужны для перечисления, то с научным прогрессом их значение возросло.

С числами можно проводить различные математические действия. С цифрами такого делать нельзя.
Число может быть отрицательным, дробным, в отличие от цифр.
Количество цифр всего 10, а чисел – бесконечное множество, т.к. они состоят из цифр.

Кроме различий, с математической точки зрения, существуют и лингвистические отличия. Они рассматривают, в каких случаях можно говорить “цифра”, а когда – “число”. Если в разговоре упоминаются официальные показатели, то уместно говорить слово “цифра”. Это могут быть, например, статистические данные.

Понятие “цифры” широко распространено в нумерологии. Нумерологи используют это понятие как знак, который способен влиять на судьбу человека. Они наделяют его мистическими свойствами. Например, нумерологи уверены в том, что некоторые цифры притягивают удачу.

Число употребляют тогда, когда нужно назвать количество чего-либо, или когда речь идет о календарной дате или дне месяца. В русском языке для употребления этого понятия применяются порядковые числительные.

По сравнению с первобытными и древними обществами, у понятия “цифра” расширилась область употребления. Теперь это – не только в математике. Сейчас люди говорят о цифровом телевидении, цифровом формате. Так же и с числами – теперь они применяются, например, в информатике. Получается, что с развитием общества и науки развиваются и математические понятия. После прочтения всех математических и лингвистических тонкостей читатели знают, чем отличается число от цифры.

Всем людям с раннего детства знакомы цифры, с помощью которых ведется счет предметов. Их всего десять: от 0 до 9. Потому и система исчисления называется десятичной. С помощью них можно записать совершенно любое число.

Тысячелетиями люди применяли свои пальцы для обозначения чисел. Сегодня десятичная система используется повсюду: для измерения времени, при продаже и покупке чего-либо, при различных расчетах. Каждый человек имеет собственные числа, например, в паспорте, на кредитной карте.

Число 1 в математике

Натуральные числа — это положительные целые числа, начиная с 1 и не имеющие десятичной части. Число 1 является начальным элементом натуральных чисел и представляет концепцию «одного» или «единицы». В математике оно используется для обозначения количества или единичной единицы измерения.

Свойства числа 1:

1. Число 1 является уникальным числом, так как оно не является простым или составным числом.

2. Число 1 является единственным натуральным числом, которое не является простым числом. Простые числа — это числа, которые имеют только два делителя: 1 и само число. Число 1 имеет только один делитель — 1, поэтому оно не является простым.

3. Число 1 может быть определено как результат сложения 0 и 1 (1 = 0 + 1) и как результат умножения любого числа на 1 (a * 1 = a).

Примеры использования числа 1 в математике:

1. В алгебре число 1 играет важную роль в операциях сложения, вычитания, умножения и деления. Например, при умножении числа на 1, результатом будет само число.

2. В геометрии число 1 используется для обозначения меры угла в радианах. Один радиан соответствует углу, под которым длина дуги окружности равна радиусу окружности.

3. В вероятностной теории число 1 обозначает вероятность наступления определенного события, если это событие является достоверным или обязательным.

Число	Сумма с числом 1	Умножение на число 1
2	3	2
5	6	5
10	11	10

Число и десятичная система счисления

Числа отличаются от цифр тем, что могут состоять как из одной, так и из нескольких цифр, записанных подряд
. Десятичная система счисления – это позиционная система. Значение цифры зависит от места (позиции), которое она занимает в числе. Цифры – это тоже числа, но состоящие из одной цифры, которая занимает позицию в разряде единиц. Если необходимо записать число, следующее по порядку за 9, то нужно перейти к следующему разряду – разряду десятков.

От пересчета предметов, который осуществляется с помощью натуральных чисел, человечество естественно перешло к счету мер длины, веса и времени. И тогда возникла проблема как считать нецелые части. Естественным образом появились обыкновенные дроби: половина, треть, четверть, пятая часть и т.п. Их стали записывать в виде числителя и знаменателя: в знаменателе записывали на сколько частей поделено целое, а в числителе – сколько таких частей берется. Например, половина – это 1/2, треть – 1/3, четверть – 1/4 и т.д.

Итоги

Еще одним ответом на вопрос о том, почему цифры называются арабскими, является тот факт, что само слово «цифра» также имеет арабское происхождение. Математики перевели слово индусов «сунья» на родной язык и получилось «сифр», что уже похоже на произносимое в наши дни.

Это все, что известно о том, почему цифры называются арабскими. Возможно, современные ученые еще сделают какие-либо открытия на этот счет и прольют свет на их возникновение. А пока люди довольствуются только этой информацией.